что такое квадрат гипотенузы
Теорема Пифагора.
Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение
между сторонами прямоугольного треугольника.
Будет полезно сохранить таблицу Пифагора.
Считается, что доказана греческим математиком Пифагором, в честь которого и названа.
Геометрическая формулировка теоремы Пифагора.
Изначально теорема была сформулирована следующим образом:
В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов,
построенных на катетах.
Алгебраическая формулировка теоремы Пифагора.
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
То есть, обозначив длину гипотенузы треугольника через c, а длины катетов через a и b:
Обе формулировки теоремы Пифагора эквивалентны, но вторая формулировка более элементарна, она не
требует понятия площади. То есть второе утверждение можно проверить, ничего не зная о площади и
Обратная теорема Пифагора.
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то
Для всякой тройки положительных чисел a, b и c, такой, что

существует прямоугольный треугольник с катетами a и b и гипотенузой c.
Теорема Пифагора для равнобедренного треугольника.
Теорема Пифагора для равностороннего треугольника.
Доказательства теоремы Пифагора.
На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема
Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие
можно объяснить лишь фундаментальным значением теоремы для геометрии.
Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них:
доказательства методом площадей, аксиоматические и экзотические доказательства (например,
с помощью дифференциальных уравнений).
1. Доказательство теоремы Пифагора через подобные треугольники.
Следующее доказательство алгебраической формулировки — наиболее простое из доказательств, строящихся
напрямую из аксиом. В частности, оно не использует понятие площади фигуры.
Пусть ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту из C и обозначим
её основание через H.
Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC.


или 
2. Доказательство теоремы Пифагора методом площадей.
Ниже приведённые доказательства, несмотря на их кажущуюся простоту, вовсе не такие простые. Все они
используют свойства площади, доказательства которых сложнее доказательства самой теоремы Пифагора.

треугольника так, как показано на рисунке
Четырёхугольник со сторонами c – квадратом,
так как сумма двух острых углов 90°, а
развёрнутый угол — 180°.
Площадь всей фигуры равна, с одной стороны,
площади квадрата со стороной (a+b), а с другой стороны, сумме площадей четырёх треугольников и
Что и требовалось доказать.
3. Доказательство теоремы Пифагора методом бесконечно малых.
Рассматривая чертёж, показанный на рисунке, и
записать следующее соотношение для бесконечно
малых приращений сторон с и a (используя подобие
Используя метод разделения переменных, находим:
Более общее выражение для изменения гипотенузы в случае приращений обоих катетов:
Интегрируя данное уравнение и используя начальные условия, получаем:
Таким образом, мы приходим к желаемому ответу:
Как нетрудно видеть, квадратичная зависимость в окончательной формуле появляется благодаря линейной
пропорциональности между сторонами треугольника и приращениями, тогда как сумма связана с независимыми
вкладами от приращения разных катетов.
Более простое доказательство можно получить, если считать, что один из катетов не испытывает приращения
(в данном случае катет b). Тогда для константы интегрирования получим:
Теорема Пифагора
Теорема Пифагора является одной из важнейших теорем в геометрии.
Формулировка у теоремы такая:
в прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов.
Зная формулировку теоремы Пифагора и две стороны прямоугольного треугольника:
два катета либо катет и гипотенузу, можно найти третью сторону треугольника,
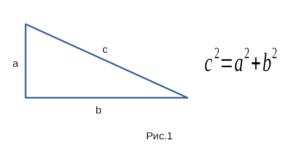
соответственно: гипотенузу либо катет. На рисунке 1 изображен
прямоугольный треугольник и формулировка теорема Пифагора.
Доказательство теоремы Пифагора
Для доказательства этой теоремы, нарисуем прямоугольный треугольник.
Ради удобства обозначим гипотенузу латинской буквой с, а катеты латинскими
буквами a и b. Докажем, что в прямоугольном треугольнике квадрат гипотенузы
равен сумме квадратов катетов, или иначе \( c^2=a^2+b^2 \).
Теорема доказана.
Следствия из теоремы Пифагора
У этой теоремы много следствий, которые используются при доказательстве
других теорем и некоторых свойств. Перечислим основные из них:
Теорема Пифагора
Основные понятия
Теорема Пифагора, определение: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Гипотенуза — сторона, лежащая напротив прямого угла.
Катет — одна из двух сторон, образующих прямой угол.
Формула Теоремы Пифагора выглядит так:
где a, b — катеты, с — гипотенуза.
Из этой формулы можно вывести следующее:
Для фигуры со сторонами a, b и c, где c самая длинная сторона действуют следующие правила:
Теорема Пифагора: доказательство
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Дано: ∆ABC, в котором ∠C = 90º.
Пошаговое доказательство:
a 2 + b 2 = c * HB + c * AH
a 2 + b 2 = c * (HB + AH)
Обратная теорема Пифагора: доказательство
Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такая фигура является прямоугольной.
Дано: ∆ABC
Доказать: ∠C = 90º
Пошаговое доказательство:
Обратная теорема доказана.
Решение задач
Задание 1. Дан прямоугольный треугольник ABC. Его катеты равны 6 см и 10 см. Какое значение у гипотенузы?
значит c 2 = a 2 + b 2 = 6 2 + 10 2 = 36 + 100 = 136
Задание 2. Является ли фигура со сторонами 8 см, 9 см и 11 см прямоугольным треугольником?
Ответ: треугольник не является прямоугольным.
Теорема Пифагора
Теорема Пифагора — квадрат гипотенузы равен сумме квадратов катетов (в прямоугольном треугольнике); формула: c² = a² + b².
Доказательство
Доказательство теоремы Пифагора, используя алгебру
Нужно доказать, что c² = a² + b²:
Это квадрат, в котором есть 4 одинаковых треугольника abc:
Что и требовалось доказать.
«Пифагоровы штаны на все стороны равны»
Это шуточная фраза, которая именует ещё одно доказательство теоремы Пифагора
На этой фигуре c — гипотенуза, a и b — катеты.
Проведём перпендикулярную линию к гипотенузе (c):
Таким образом появились два новых прямоугольных треугольника (A и B) внутри большого (исходный треугольник С).
Что и требовалось доказать.
Примеры
Задача 1
На рисунке видно, что длина одной стороны прямоугольного треугольника составляет 3 см, длина другой — 4 см. Найдите длину гипотенузы.
Подставить известные значения
Ответ: длина гипотенузы равна 5.
Задача 2
Длина одной стороны прямоугольного треугольника составляет 12 см, длина гипотенузы 13 см. Найдите длину другой стороны треугольника.
Подставить известные значения
Ответ: длина другой стороны треугольника равна 5.
Следствия из теоремы Пифагора
Это основные следствия теоремы:
Кто придумал теорему Пифагора
Концепция теоремы Пифагора была известна ещё в древнем Египте и Вавилоне (около 1900 г. до н. э.). Связь между катетами и гипотенузой в прямоугольном треугольнике была изображена на вавилонской глиняной табличке (которой около 4000 лет). Однако это знание стало широко использоваться лишь после того, как сам Пифагор заявил о нём (он жил в 6 веке до н. э.).
Узнайте также, что такое Теорема Виета и Аксиома.
Теорема Пифагора онлайн
С помощю этого онлайн калькулятора можно найти неизвестную сторону прямоугольного треугольника используя теорему Пифагора. Теоретическую часть и численные примеры смотрите ниже.
Теорема Пифагора. Доказательство
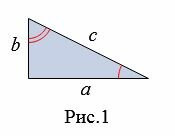  |
Доказательство (метод площадей). Пусть задан прямоугольный треугольник с катетами a и b и гипотенузой c (Рис.1). Докажем, что \( \small c^2=a^2+b^2. \)
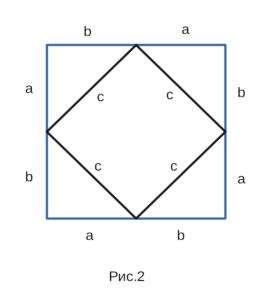
Построим квадрат со стороной a+b из четырех таких прямоугольных треугольников (Рис.2). Тогда внутренний белый четырехугольник будет квадратом со стороной c.
Действительно. В прямоугольных треугольниках (Рис.2) \( \small \angle 1 +\angle 2=90° \) Следовательно, каждый угол квадрата со стороной c равен \( \small \angle 3=180°-(\angle 1 +\angle 2)=180°-90°=90°.\)
Далее, площадь квадрата со стороной a+b равна:
Площадь квадрата со стороной c равна:
Площадь каждого прямоугольного треугольника на рисунке 2 равна:
Площадь квадрата со стороной a+b равна сумме площади квадрата со стороной c и четырех площадей прямоугольных треугольников c катетами a и b:
Подставляя (1)-(3) в (4), получим:
| \( \small (a+b)^2=с^2+4 \cdot \frac12ab, \) |
| \( \small a^2+2ab+b^2=с^2+2ab, \) |
\( \small a^2+b^2=с^2. \) |
 |
Сложив уравнения (5) и (6), получим
Доказательство (Евклид). Пусть задан прямоугольный треугольник ABC с катетами a, b и гипотенузой c (Рис.4). Докажем, что \( \small c^2=a^2+b^2. \)
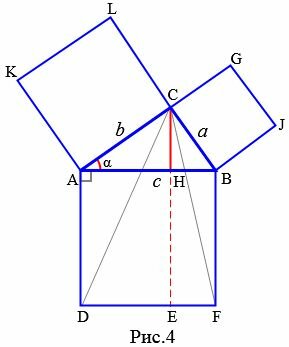 |
Достаточно доказать, что площадь квадрата ABFD равна сумме площадей ACLK и BCGJ:
Площадь треугольника ACD по двум сторонам и углу между ними равен:
Учитывая, что \( \small \sin \angle ACH=\sin (90°-\alpha)=\sin \alpha, \) применим теорему синусов для прямоугольного треугольника ACH:
Подставляя (8) в (7), получим:
Применим теорему синусов для прямоугольного треугольника ABC:
Подставляя (10) в (7), получим:
Учитывая, что \( \small AD=AB, \) получим:
Аналогично можно показать, что
Сложив (13) и (14), получим:
Теорема Пифагора. Примеры и решения
Решение: Для нахождения гипотенузы воспользуемся формулой Пифагора:
Подставляя значения \( \small a \) и \( \small b \) в (15), получим:
 |
Ответ:
Решение: Для нахождения неизвестного катета воспользуемся теоремой Пифагора:
Подставляя значения \( \small a \) и \( \small b \) в (16), получим:
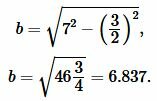 |
Ответ: