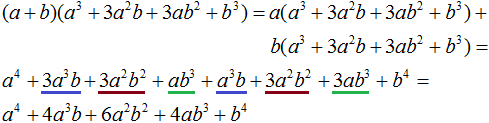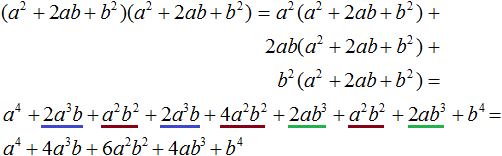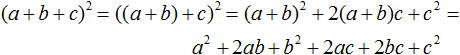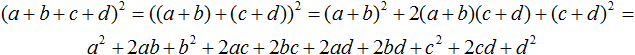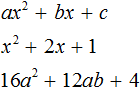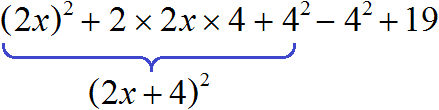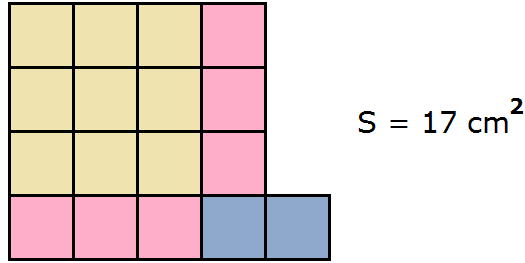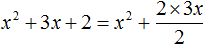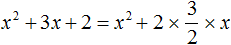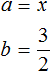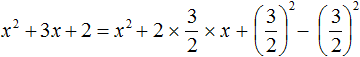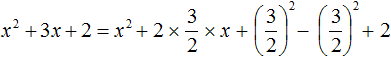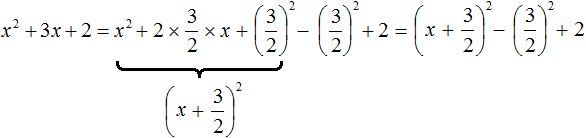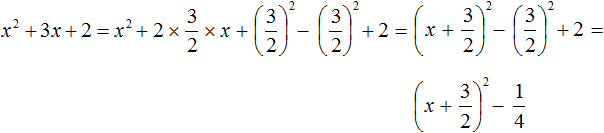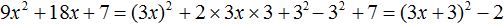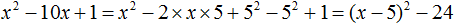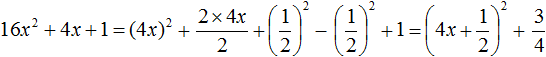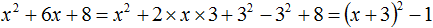что такое квадрат двучлена

Формулы сокращенного умножения. Разложение на множители.

теория по математике 📈 алгебраические выражения

Очень часто нам встречаются выражения, которые требуют различных преобразований. Для того, чтобы это короче выполнять в некоторых случаях, существуют специальные формулы сокращенного умножения.

Квадрат суммы и квадрат разности

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений плюс квадрат второго выражения:

(a+b) 2 =a 2 +2ab+b 2

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений плюс квадрат второго выражения:

(a–b) 2 =a 2 –2ab+b 2

Если сравнить два этих правила и формулы, то видно, что при возведении в квадрат есть отличие в знаках только перед удвоенным произведением. Рассмотрим применение данных формул на примерах.

Куб суммы и разности

Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения и второго плюс утроенное произведение первого выражения и квадрата второго плюс куб второго выражения:

(a+b) 3 =a 3 +3a 2 b+3ab 2 +b 3

Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения и второго плюс утроенное произведение первого выражения и квадрата второго минус куб второго выражения:

(a–b) 3 =a 3 –3a 2 b+3ab 2 –b 3

Используя данные формулы, можно возводить в куб сумму и разность двух выражений. В данном случае не нужно выполнять промежуточные действия устно, чтобы избежать ошибок.

Пример №5. Возведем в куб сумму с+5а. Всё выполним и распишем строго по формуле:

Пример №6. Возведем в куб разность:

(х–10) 3 =х 3 –3х 2 10+3х10 2 –10 3 =х 3 –30х 2 +300х–1000.

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений:

a 2 –b 2 =(a–b)(a+b)

Пример №7. Выполним умножение: (4–с)(4+с)=4 2 –с 2 =16–с 2 в данном выражении выполнили всё в соответствии с формулой: возвели в квадрат 4 и число с. Промежуточные записи (выделены жирным шрифтом) можно не делать, а выполнять их устно.

Пример №8. Упростим выражение: (5с+а)(5с–а)=25с 2 –а 2 в данном выражении мы видим, что первый множитель сумма, а второй – разность. Для выполнения задания по данной формуле это не имеет значения, так как мы знаем, что от перестановки множителей произведение не изменяется.

Применение формул сокращенного умножения для разложения многочленов на множители

Рассмотрим тождество, которое называют разностью квадратов двух выражений:

a 2 –b 2 =(a–b)(a+b)

Разность квадратов двух выражений равна произведению разности этих выражений и их суммы. Эту формулу применяют для разложения на множители многочлена, содержащего разность квадратов. Рассмотрим на примерах.

Пример №10. Разложить на множители: х 2 у 2 –81=(ху–9)(ху+9). В данном выражении выполнено всё в соответствии с формулой, промежуточные записи не использованы.

Пример №11. Представим в виде произведения: х 4 –36=(х 2 –6)(х 2 +6). В данном выражении мы видим, что степень переменной может быть не только вторая, но и любая четная, чтобы ее можно было представить в виде квадрата переменной.

Пример №12. Представим в виде произведения х 10 с 6 –25=(х 5 с 3 –5)(х 5 с 3 +5). Здесь показаны разные четные степени переменных.

Для разложения на множители суммы и разности кубов существуют определенные правила и формулы.

Сумма и разность кубов

Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности:

a 3 +b 3 =(a+b)(a 2 –ab+b 2 )

Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы:

a 3 –b 3 =(a–b)(a 2 +ab+b 2 )

Разложение многочлена формулой квадрата суммы и разности

Формулы квадрата суммы и квадрата разности также используют для разложения многочлена на множители. Для этого формулы записываются в обратном порядке, то есть меняются левая и правая части местами:

a 2 +2ab+b 2 =(a+b) 2

a 2 –2ab+b 2 =(a–b) 2

P.S. Все формулы на одной картинке:

В данном случае необходимо сначала упростить выражение, для этого раскроем скобки:

(x + 5) 2 — x (x — 10) = x 2 + 2 • 5 • x + 25 — x 2 + 10x

Затем приведем подобные слагаемые:

x 2 + 2 • 5 • x + 25 — x 2 + 10x = 20 x + 25

Далее подставим x из условия:

20 x + 25 = 20 • (-1/20) + 25 = — 1 + 25 = 24

pазбирался: Даниил Романович | обсудить разбор | оценить

Источник

Тождественные преобразования многочленов

Возведение двучлена в степень

Двучлен — это многочлен, состоящий из двух членов. В прошлых уроках мы возводили двучлен во вторую и третью степень, тем самым получили формулы сокращенного умножения:

Но двучлен можно возводить не только во вторую и третью степень, но и в четвёртую, пятую или более высокую степень.

К примеру, возведём двучлен a + b в четвертую степень:

Представим это выражение в виде произведения двучлена a + b и куба этого же двучлена

Сомножитель (a + b) 3 можно заменить на правую часть формулы куба суммы двух выражений. Тогда получим:

А это обычное перемножение многочленов. Выполним его:

То есть при возведении двучлена a + b в четвертую степень получается многочлен a 4 + 4a 3 b + 6a 2 b 2 + 4ab 3 + b 4

Возведение двучлена a + b в четвертую степень можно выполнить ещё и так: представить выражение (a + b) 4 в виде произведения степеней (a + b) 2 (a + b) 2

А это опять же обычное перемножение многочленов. Выполним его. У нас получится тот же результат, что и раньше:

Возведение трёхчлена в степень

Трёхчлен — это многочлен, состоящий из трёх членов. Например, выражение a + b + c является трёхчленом.

Иногда может возникнуть задача возвести трёхчлен в степень. Например, возведём в квадрат трехчлен a + b + c

Два члена внутри скобок можно заключить в скобки. К примеру, заключим сумму a + b в скобки:

В этом случае сумма a + b будет рассматриваться как один член. Тогда получается, что в квадрат мы возводим не трёхчлен, а двучлен. Сумма a + b будет первым членом, а член c — вторым членом. А как возводить в квадрат двучлен мы уже знаем. Для этого можно воспользоваться формулой квадрата суммы двух выражений:

Применим эту формулу к нашему примеру:

Таким же способом можно возвести в квадрат многочлен, состоящий из четырёх и более членов. Например, возведем в квадрат многочлен a + b + c + d

Теперь воспользуемся формулой квадрата суммы двух выражений:

Выделение полного квадрата из квадратного трёхчлена

Ещё одно тождественное преобразование, которое может пригодиться при решении задач это выделение полного квадрата из квадратного трёхчлена.

Квадратным трехчленом называют трёхчлен второй степени. Например, следующие трехчлены являются квадратными:

Итак, переменная a равна 2x

Отсюда делаем вывод, что переменная b равна 4

Значит, нашим полным квадратом будет выражение (2x) 2 + 2 × 2x × 4 + 4 2

Итак, возвратимся к исходному трехчлену 4x 2 + 16x + 19 и попробуем аккуратно внедрить в него полученный нами полный квадрат (2x) 2 + 2 × 2x × 4 + 4 2

Вместо 4x 2 записываем (2x) 2

Далее вместо 16x записываем удвоенное произведение, а именно 2 × 2x × 4

Далее прибавляем квадрат второго выражения:

А член 19 пока переписываем как есть:

4x 2 + 16x + 19 = (2x) 2 + 2 × 2x × 4 + 4 2 + 19

(2x) 2 + 2 × 2x × 4 + 4 2 + 19 = 4x 2 + 16x + 4 2 + 19

Чтобы сохранить значение исходного многочлена, нужно после прибавления члена 4 2 сразу же вычесть его

4x 2 + 16x + 19 = (2x) 2 + 2 × 2x × 4 + 4 2 − 4 2 + 19

4x 2 + 16x + 19 = (2x) 2 + 2 × 2x × 4 + 4 2 − 4 2 + 19 = (2x + 4) 2 − 4 2 + 19

4x 2 + 16x + 19 = (2x) 2 + 2 × 2x × 4 + 4 2 − 4 2 + 19 = (2x + 4) 2 − 4 2 + 19 = (2x + 4) 2 + 3

Значит, 4x 2 + 16x + 19 = (2x + 4) 2 + 3

Пример 2. Выделить полный квадрат из квадратного трёхчлена x 2 + 2x + 2

Следующий член исходного трёхчлена 2x перепишем в виде удвоенного произведение первого выражения (это у нас x ) и второго выражения b (это будет 1).

Теперь вернёмся к исходному квадратному трёхчлену и внедрим в него полный квадрата x 2 + 2x + 1 2

x 2 + 2x + 2 = x 2 + 2x + 1 2 − 1 2 + 2 = (x + 1) 2 + 1

Как и в прошлом примере член b (в данном примере это 1) после прибавления сразу был вычтен с целью сохранения значения исходного трёхчлена.

Рассмотрим следующее числовое выражение:

Значение этого выражения равно 17

Второй член 6 представим в виде удвоенного произведения первого члена 3 и второго 1

3 2 + 6 + 2 = 3 2 + 2 × 3 × 1 + 1 2 − 1 2 + 2

Свернем полный квадрат, а члены −1 2 и 2 слóжим:

3 2 + 6 + 2 = 3 2 + 2 × 3 × 1 + 1 2 − 1 2 + 2 = (3 + 1) 2 + 1

(3 + 1) 2 +1 = 4 2 + 1 = 17

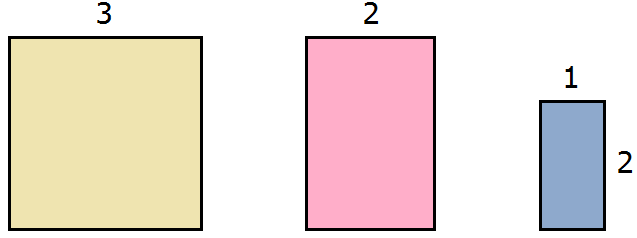
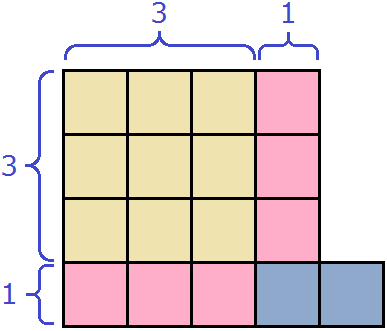
Допустим, у нас имеются квадрат и два прямоугольника. Квадрат со стороной 3 см, прямоугольник со сторонами 2 см и 3 см, а также прямоугольник со сторонами 1 см и 2 см

Запишем сумму площадей этих прямоугольников:

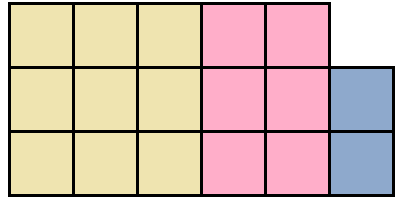
Это выражение можно понимать как объединение квадрата и двух прямоугольников в единую фигуру:

Попробуем из имеющейся фигуры образовать квадрат. Причем максимально большой квадрат. Для этого будем использовать части от розового и сиреневого прямоугольника.

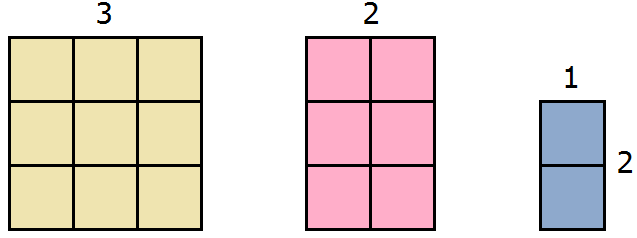
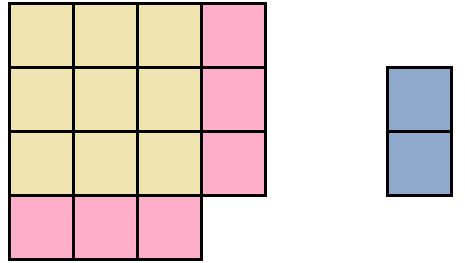
Чтобы образовать максимально большой квадрат из имеющейся фигуры, можно желтый квадрат оставить без изменений, а половину от розового прямоугольника прикрепить к нижней части желтого квадрата:

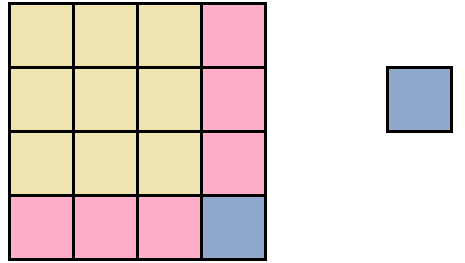
Видим, что до образования полного квадрата не хватает еще одного квадратного сантиметра. Его мы можем взять от сиреневого прямоугольника. Итак, возьмем один квадрат от сиреневого прямоугольника и прикрепим его к образуемому большому квадрату:

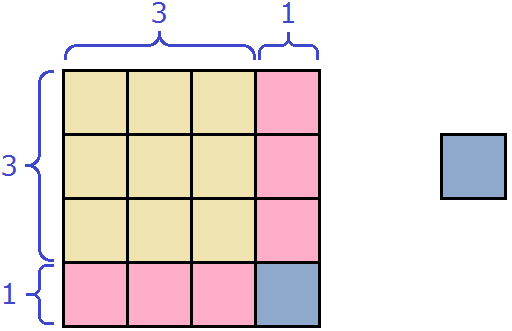
Теперь внимательно посмотрим к чему мы пришли. А именно на желтую часть фигуры и розовую часть, которая по сути увеличила прежний жёлтый квадрат. Не означает ли это то, что была сторона квадрата равная 3 см, и эта сторона была увеличена на 1 см, что привело в итоге к увеличению площади?

(3 + 1) 2

(3 + 1) 2 = 3 2 + 6 + 1 = 9 + 6 + 1 = 16

Действительно, в образовавшемся квадрате содержится 16 квадратов.

Оставшийся один квадратик от сиреневого прямоугольника можно прикрепить к образовавшемуся большому квадрату. Ведь речь изначально шла о единой фигуре:

(3 + 1) 2 + 1

9 + 6 + 2 = 3 2 + 6 + 2 = 3 2 + 2 × 3 × 1 + 1 2 − 1 2 + 2 = (3 + 1) 2 + 1

Пример 4. Выполним выделение полного квадрата из квадратного трёхчлена x 2 + 6x + 8

x 2 + 6x + 8 = x 2 + 2 × x × 3 + 3 2 − 3 2 + 8 = (x + 3) 2 − 1

Например, выполним выделение полного квадрата из квадратного трёхчлена x 2 + 3x + 2

Возвращаемся к нашему примеру и прибавляем квадрат второго выражения, и чтобы значение выражения не изменилось, сразу же вычитаем его:

Прибавляем оставшийся член 2

Свернём полный квадрат:

Оставшийся квадрат второго выражения и число 2 можно сложить. В итоге получим:

Пример 6. Выполним выделение полного квадрата из квадратного трёхчлена 9x 2 + 18x + 7

Пример 7. Выполним выделение полного квадрата из квадратного трёхчлена x 2 − 10x + 1

Пример 8. Выполним выделение полного квадрата из квадратного трёхчлена 16x 2 + 4x + 1

Пример 9. Разложить многочлен x 2 + 6x + 8 на множители при помощи выделения полного квадрата.

Сначала выделим полный квадрат:

Источник

Сокращенное умножение: правила, формулы

Формулы сокращенного умножения

Вместо букв a, b могут быть любые числа, переменные или даже целые выражения. Для быстрого решения задач лучше выучить основные 7 формул сокращенного умножения (ФСУ) наизусть. Да, алгебра такая, нужно быть готовым много запоминать.

Ниже удобная табличка, которую можно распечатать и использовать, как закладку для быстрого запоминания формул.

Как читать формулы сокращенного умножения

Учимся проговаривать формулы сокращенного выражения:

Доказательство формул сокращенного умножения

Остальные ФСУ можно доказать аналогичным методом.

Дополнительные формулы сокращенного умножения

К таблице основных ФСУ следует добавить еще несколько важных тождеств, которые пригодятся для решения задач.

Бином Ньютона

Формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Записывается вот так:

Пример вычисления биномиальных коэффициентов, которые стоят в строке под номером n в треугольнике Паскаля:

ФСУ для квадрата и куба суммы и разности — являются частными случаями формулы бинома Ньютона при n = 2 и n = 3.

Формула возведения в квадрат суммы трех, четырех и более слагаемых

Пригодится, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два.

Читается так: квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых и удвоенных произведений всех возможных пар этих слагаемых.

Формула разности n-ых степеней двух слагаемых

a n − b n = (a − b) * (a n-1 + a n-2 * b + a n-3 * b 2 + … + a * b n-2 + b n-1 ).

Для четных показателей можно записать так:

a 2*m − b 2*m = (a 2 − b 2 ) *(a 2*m−2 + a 2*m−4 * b 2 + a 2*m−6 * b 4 + … + b 2*m−2 ).

Для нечетных показателей:

a 2*m+1 − b 2*·m+1 = (a − b) * (a 2*m + a 2*m−1 * b + a 2*m−2 * b 2 + … + b 2*m ).

Частными случаями являются формулы разности квадратов и кубов при n = 2 и n = 3. Для разности кубов b можно также заменить на −b.

Решение задач

Давайте потренируемся и рассмотрим примеры с дробями.

Задание 1

Как решаем: воспользуемся формулой квадрата суммы: (55 + 10) 2 = 55 2 + 2 * 55 * 10 + 10 2 = 3025 + 1100 + 100 = 4225.

Задание 2

Что сделать: упростить выражение 64 * с 3 – 8.

Как решаем: применим разность кубов: 64 * с 3 – 8 = (4 * с) 3 – 2 3 = (4 * с – 2)((4 * с) 2 + 4 * с * 2 + 2 2 ) = (4 * с – 2)(16 * с 2 + 8 * с + 4).

Задание 3

Как решаем:

Многочленов бояться не стоит, просто совершайте последовательно каждое действие. С формулами решать задачки быстрее и удобнее — сохраняйте шпаргалку, запоминайте и радуйте своих учителей 🙂

Источник