что такое кубический корень

Кубический корень

Содержание

Свойства

Кубический корень — нечётная функция. В отличие от квадратного корня, кубический может быть извлечён и из отрицательных чисел:

Общее правило — из отрицательных чисел корни нечётной степени (в том числе и кубический) извлекаются, корни чётной степени — нет. Данное утверждение справедливо только для диапазона вещественных чисел.

Кубический корень из комплексного числа (из любого числа) имеет ровно три значения (частный случай свойства корня n-ой степени):

Здесь под понимается арифметический корень из положительного числа

Два комплексных значения кубического корня получаются из вещественных по формуле:

Эти значения необходимо знать для решения кубических уравнений по формуле Кардано.

Интересные факты

Кубический корень не может быть извлечён с помощью циркуля и линейки. Именно поэтому неразрешимы сводимые к извлечению кубического корня классические задачи: удвоение куба, трисекция угла, а также построение правильного семиугольника.

При постоянной плотности вещества размеры двух подобных тел относятся друг к другу как кубические корни их масс. Так, если один арбуз весит вдвое больше, чем другой, то его диаметр (а также окружность) будет всего лишь чуть больше, чем на четверть (на 26%) больше, чем у первого; и на глаз будет казаться, что разница в весе не столь существенна. Поэтому при отсутствии весов (продажа на глазок) обычно более выгодно покупать бо́льший плод.

См. также

Литература

Полезное

Смотреть что такое «Кубический корень» в других словарях:

кубический корень — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN third root … Справочник технического переводчика

КУБИЧЕСКИЙ — (от слова куб). 1) имеющий вид куба. 2) мера, имеющая форму куба, т. е. правильного шестигранника. 3) корень, всякая величина, которая, будучи помножена три раза сама на себя, дает данную величину. Словарь иностранных слов, вошедших в состав… … Словарь иностранных слов русского языка

КОРЕНЬ КУБИЧЕСКИЙ — (обозначение 3Ц), число, которое необходимо дважды умножить на само себя для получения заданного числа. Например, кубический корень из 64 равняется 4, поскольку 4x4x4 = 64. В этом случае записывают: 3Ц64 = 4. В терминах алгебры кубический корень… … Научно-технический энциклопедический словарь

кубический — КУБИЧЕСКИЙ, КУБИЧНЫЙ ая, ое. cubique adj. <, лат. cubicus. 1. Имеющий форму куба. шестигранника. Сл. 18. Большая голова кубической фигуры. С. Меран 20. Горница имела совершенно кубический вид. ТВЭО 50 14. 2. Связанный с объемом, измерением… … Исторический словарь галлицизмов русского языка

КОРЕНЬ — КОРЕНЬ, корня, мн. корни, корней, м. 1. Вросшая в землю часть растения, через к рую оно всасывает соки из почвы. Бурей выворотило деревья с корнями. Дуб глубоко пустил корни в землю. || Древесина или вещество этой части растения. Лакричный корень … Толковый словарь Ушакова

КУБИЧЕСКИЙ — КУБИЧЕСКИЙ, кубическая, кубическое. 1. прил. к куб1 в 1 и 4 знач. (мат.). Кубическая форма. Кубическая степень. Извлечь кубический корень. 2. Выраженный в мерах, за единицу объема которых принят куб. Кубическая система мер. Кубический метр.… … Толковый словарь Ушакова

КОРЕНЬ ЧИСЛА — (root of number) Число х, чье значение в степени r равно у. Если у=хr, то х – корень r – степени от у. Например, в уравнении у=х2, х является квадратным корнем из у, и записывается следующим образом: x=√ y=y1/2; если z=x3, то х – кубический… … Экономический словарь

Корень (значения) — Корень: В Викисловаре есть статья «корень» Корень (в ботанике) вегетативный осевой подземный орган растения, обладающий сп … Википедия

корень — сущ., м., употр. сравн. часто Морфология: (нет) чего? корня, чему? корню, (вижу) что? корень, чем? корнем, о чём? о корне и на корню; мн. что? корни, (нет) чего? корней, чему? корням, (вижу) что? корни, чем? корнями, о чём? о корнях 1. Корень это … Толковый словарь Дмитриева

Кубический закон взаимности — Характер кубического вычета – теоретико числовая функция двух аргументов, являющаяся частным случаем символа степенного вычета. Также является характером в простом поле. Характер кубического вычета является аналогом символа Лежандра, и для его… … Википедия

Источник

Корни и степени

Здесь — основание степени, — показатель степени.

Степень с натуральным показателем

Проще всего определяется степень с натуральным (то есть целым положительным) показателем.

Выражения «возвести в квадрат» и «возвести в куб» нам давно знакомы.
Возвести число в квадрат — значит умножить его само на себя.

Возвести число в куб — значит умножить его само на себя три раза.

Возвести число в натуральную степень — значит умножить его само на себя раз:

Степень с целым показателем

Показатель степени может быть не только натуральным (то есть целым положительным), но и равным нулю, а также целым отрицательным.

Определим также, что такое степень с целым отрицательным показателем.

Заметим, что при возведении в минус первую степень дробь переворачивается.

Свойства арифметического квадратного корня:

Кубический корень

Обратите внимание, что корень третьей степени можно извлекать как из положительных, так и из отрицательных чисел.

Заметим, что корень третьей, пятой, девятой — словом, любой нечетной степени, — можно извлекать как из положительных, так и из отрицательных чисел.

Квадратный корень, а также корень четвертой, десятой, в общем, любой четной степени можно извлекать только из неотрицательных чисел.

Сразу договоримся, что основание степени больше 0.

При этом также выполняется условие, что больше 0.

Запомним правила действий со степенями:

— при перемножении степеней показатели складываются

— при делении степени на степень показатели вычитаются

— при возведении степени в степень показатели перемножаются

Ты нашел то, что искал? Поделись с друзьями!

Покажем, как применяются эти формулы в заданиях ЕГЭ по математике:

Внесли все под общий корень, разложили на множители, сократили дробь и извлекли корень.

Здесь мы записали корни в виде степеней и использовали формулы действий со степенями.

Это полезно

В нашей статье вы найдете всю необходимую теорию для решения задания №9 ЕГЭ по теме «Графики функций». Это задание появилось в 2022 году в вариантах ЕГЭ Профильного уровня.

Источник

Вычисление кубического корня

Кубический корень числа А — это такое число В, которое при возведении в третью степень в результате дает число А. Вычисление кубического корня — более сложная задача, нежели поиск квадратных корней.

Обозначение

Корни чисел ранее обозначались символом Rx, от латинского слова radix, то есть корень. Именно поэтому синонимом арифметических корней стало слово «радикал». Позднее для удобства типографской записи корни стали обозначаться латинской буквой V, а надстрочный знак перед символом указывает на степень корня. Для упрощения обозначения кубических корней в этой статье мы будем использовать слово cube. Это означает, что cube(8) следует читать как «кубический корень из 8».

Алгоритм приблизительных вычислений

Кубический корень положительного или отрицательного числа А — это соответственно положительное или отрицательное В, которое при возведении в куб дает число А. Пусть требуется найти cube(27).

Кубическая последовательность растет довольно быстро, и в отличие от квадратов чисел, куб может оканчиваться на любую цифру. Так как количество натуральных чисел уходит в бесконечность, то и количество кубов также бесконечно, однако целочисленных значений все же гораздо меньше, чем иррациональных.

Наша программа представляет собой универсальный калькулятор вычисления корней любой степени. Для того, чтобы вычислить значение кубического корня вам потребуется указать заданное число в ячейку «Число(x)», а ячейке «Степень(n)» требуется ввести значение степени. По умолчанию калькулятор выставляет в «Степень(n)» число 3, поэтому вы сразу можете вычислять кубические корни, не устанавливая степень корня.

Пример работы калькулятора

Вычисление ребра куба

Классическая задача на вычисление кубического корня — это определение длины ребра куба, если известен его объем. Для значений объема из кубической последовательности все просто, так как ответ будет записан в виде целого числа. Для всех остальных значений нам пригодится онлайн-калькулятор. Давайте вычислим длины ребер для следующих объемов кубов:

Как видите, в диапазоне от 10 до 100 длина ребра изменятся всего на 2,5 пункта.

Заключение

Поиск кубического корня — сложная задача, если вычислять значение требуется для больших или некубических чисел. Для определения значения кубического корня заданной точности используйте наш онлайн-калькулятор — простой инструмент для быстрых вычислений, который идеально подойдет школьникам и студентам.

Источник

Простые и не очень способы того, как вычислить кубический корень

Сколько гневных слов произнесено в его адрес? Порой кажется, что кубический корень невероятно сильно отличается от квадратного. На самом деле разница не настолько велика. Особенно, если понять, что они только частные случаи общего корня n-ой степени.

Зато с его извлечением могут возникнуть проблемы. Но чаще всего они связаны с громоздкостью вычислений.

Что нужно знать о корне произвольной степени?

Во-первых, определение этого понятия. Корнем n-ой степени из некоторого «а» называется такое число, которое при возведении в степень n дает исходное «а».

Причем бывают четные и нечетные степени у корней. Если n — четное, то подкоренное выражение может быть только нулем или положительным числом. В противном случае вещественного ответа не будет.

Когда же степень нечетная, то существует решение при любом значении «а». Оно вполне может быть и отрицательным.

Во-вторых, функцию корня всегда можно записать, как степень, показателем которой является дробь. Иногда это бывает очень удобным.

Например, «а» в степени 1/n как раз и будет корнем n-ой степени из «а». В этом случае основание степени всегда больше нуля.

Аналогично «а» в степени n/m будет представлено, как корень m-ой степени из «а n ».

В-третьих, для них справедливы все действия со степенями.

В чем сходства и различия квадратного и кубического корней?

Они похожи, как родные братья, только степень у них разная. И принцип их вычисления одинаков, различие только в том, сколько раз должно число на себя умножиться, чтобы получить подкоренное выражение.

А о существенном отличии было сказано чуть выше. Но повториться не будет лишним. Квадратный извлекается только из неотрицательного числа. В то время, как вычислить кубический корень из отрицательной величины не составит труда.

Извлечение кубического корня на калькуляторе

Каждый человек хоть раз делал это для квадратного корня. А как быть если степень «3»?

На обычном калькуляторе имеется только кнопочка для квадратного, а кубического — нет. Здесь поможет простой перебор чисел, которые трижды умножаются на себя. Получилось подкоренное выражение? Значит, это ответ. Не получилось? Подбирать снова.

А что в инженерном виде калькулятора в компьютере? Ура, здесь есть кубический корень. Эту кнопочку можно просто нажать, и программа выдаст ответ. Но это не все. Здесь можно вычислить корень не только 2 и 3 степени, но и любой произвольной. Потому что есть кнопка у которой в степени корня стоит «у». То есть после нажатия этой клавиши потребуется ввести еще одно число, которое будет равно степени корня, а уже потом «=».

Извлечение кубического корня вручную

Этот способ потребуется, когда калькулятора под рукой нет или воспользоваться им нельзя. Тогда для того чтобы вычислить кубический корень из числа, потребуется приложить усилия.

Сначала посмотреть, а не получается ли полный куб от какого-нибудь целого значения. Может быть под корнем стоит 2, 3, 5 или 10 в третьей степени?

В противном случае нужно будет считать столбиком. Алгоритм не самый простой. Но если немного попрактиковаться, то действия легко запомнятся. И вычислить кубический корень больше не будет проблемой.

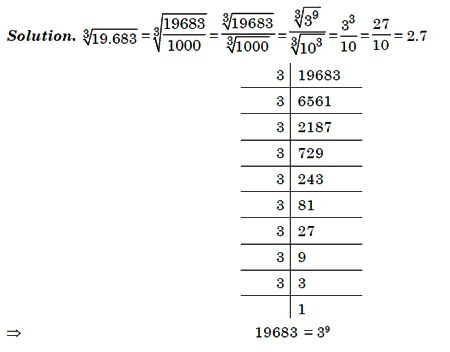
Наглядный пример вычисления кубического корня

Он нужен потому, что описание может показаться сложным. На рисунке ниже показано, как извлечь кубический корень из 15 с точностью до сотых.

Единственной сложностью, которую имеет этот метод, заключается в том, что с каждым шагом числа увеличиваются многократно и считать в столбик становится все сложнее.

Источник

Свойства корней (ОГЭ, ЕГЭ 2022)

А сейчас мы рассмотрим свойства корней.

Квадратный корень, кубический корень и корень в N-ой степени.

Порешаем задачки, чтобы к концу этого занятия все, что касается корней (в любой степени) было тебе абсолютно понятно!

И, самое главное, чтобы ты смог решить любую задачу c корнями на экзамене!Поехали!

Свойства корней — коротко о главном

Квадратным корнем (арифметическим квадратным корнем) из неотрицательного числа \( a\) называется такое неотрицательное число, квадрат которого равен \( a\)

Свойства корней:

Для любого натурального \( n\), целого \( k\) и любых неотрицательных чисел \( a\) и \( b\) выполнены равенства:

Арифметический квадратный корень

Когда ты разберешься в этой теме, тебе станет намного легче решать иррациональные уравнения и неравенства.

А пока что давай попробуем разобраться, что это за понятие «корень» и с чем его едят 🙂

Для этого рассмотрим примеры, с которыми ты уже сталкивался на уроках (ну, или тебе с этим только предстоит столкнуться).

К примеру, перед нами уравнение \( <^<2>>=4\). Какое решение у данного уравнения? Какие числа можно возвести в квадрат и получить при этом \( 4\)?

Для упрощения, математики ввели специальное понятие квадратного корня и присвоили ему специальный символ \( \sqrt<\ \ >\).

Дадим определение арифметическому квадратному корню.

Квадратным корнем (арифметическим квадратным корнем) из неотрицательного числа \( a\) называется такое неотрицательное число, квадрат которого равен \( a\)
\( \left( \sqrt=x,\ <^<2>>=a;\ \ x,a\ge 0 \right)\)

А почему же число \( a\) должно быть обязательно неотрицательным?

Например, чему равен \( \sqrt<-9>\). Так-так, попробуем подобрать. Может, три?

Это надо запомнить: число или выражение под знаком корня должно быть неотрицательным!

Однако самые внимательные уже наверняка заметили, что в определении сказано, что решение квадратного корня из «числа \( a\) называется такое неотрицательное число, квадрат которого равен \( a\)».

Такое замечание вполне уместно. Здесь необходимо просто разграничить понятия квадратных уравнений и арифметического квадратного корня из числа.

Квадратное уравнение или квадратный корень?

К примеру, \( <^<2>>=4\) не равносильно выражению \( x=\sqrt<4>\).

Из \( <^<2>>=4\) следует, что \( \left| x \right|=\sqrt<4>\), то есть \( x=\pm \sqrt<4>=\pm 2\) или \( <_<1>>=2;\ <_<2>>=-2\).

А из \( x=\sqrt<4>\) следует, что \( x=2\).

Конечно, это очень путает, но это необходимо запомнить, что знаки являются результатом решения уравнения, так как при решении уравнения мы должны записать все иксы, которые при подстановке в исходное уравнение дадут верный результат.

Однако, если просто извлекать квадратный корень из чего-либо, то всегда получаем один неотрицательный результат.

А теперь попробуй решить такое уравнение \( <^<2>>=3\).

Уже все не так просто и гладко, правда? Попробуй перебрать числа, может, что-то и выгорит?

Начнем с самого начала – с нуля: \( <<0>^<2>>=0\) – не подходит.

Двигаемся дальше \( \text=1;\ <<1>^<2>>=1\) – меньше трех, тоже отметаем.

А что если \( x=2\); \( <<2>^<2>>=4\) – тоже не подходит, т.к. это больше трех.

С отрицательными числами получится такая же история.

И что же теперь делать? Неужели перебор нам ничего не дал?

Кроме того, очевидно, что решения не будут целыми числами. Более того, они не являются рациональными. И что дальше?

Давай построим график функции \( y=<^<2>>\) и отметим на нем решения. (Прочти по ссылке как использовать график функции для решения уравнений)

Давай попробуем обмануть систему и получить ответ с помощью калькулятора! Извлечем корень из \( 3\), делов-то! Ой-ой-ой, выходит, что \( \sqrt<3>=1,732050807568…\).

Такое число никогда не кончается.

Такие числа называются иррациональными, именно для упрощения записи таких чисел и было введено понятие квадратного корня.

Рассмотрим еще один пример для закрепления.

Разберем такую задачку: тебе необходимо пересечь по диагонали квадратное поле со стороной \( \displaystyle 1\) км, сколько км тебе предстоит пройти?

Самое очевидное здесь рассмотреть отдельно треугольник и воспользоваться теоремой Пифагора: \( <^<2>>=<^<2>>+<^<2>>\). Таким образом, \( <^<2>>=1+1=2\).

Так чему же здесь равно искомое расстояние?

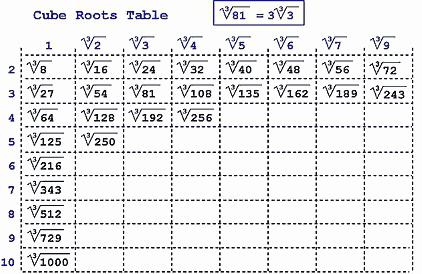
Чтобы решение примеров с корнями не вызывало проблем, необходимо их видеть и узнавать. Для этого необходимо знать, по меньшей мере, квадраты чисел от \( 1\) до \( 20\), а также уметь их распознать.

К примеру, необходимо знать, что \( 15\) в квадрате равно \( 225\), а также, наоборот, что \( 225\) – это \( 15\) в квадрате.

Вот тебе полная таблица квадратов чисел. Сверху строка — основание степени, слева в столбик показатель степени, на пересечение искомое значение степени. Запомнить нужно только то, что выделено зеленым.

Уловил, что такое квадратный корень? Тогда порешай несколько примеров.

Источник