что такое круговой сектор

Что такое круговой сектор

Круг — это часть плоскости, ограниченная окружностью. Центр данной окружности называется центром круга, а расстояние от центра до любой точки окружности — радиусом круга:

O — центр круга, OA — радиус круга.

Площадь круга

Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга:

где S — площадь круга, а r — радиус круга.

Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:

Следовательно, формула нахождения площади круга через диаметр будет выглядеть так:

Сектор круга. Площадь сектора

Сектор — это часть круга, ограниченная двумя радиусами и дугой. Два радиуса разделяют круг на два сектора:

Чтобы найти площадь сектора, дуга которого содержит n°, надо площадь круга разделить на 360 и полученный результат умножить на n.

Формула площади сектора:

где S — площадь сектора. Выражение

можно представить в виде произведения

Следовательно, площадь сектора равна длине дуги сектора, умноженной на половину радиуса:

где S — это площадь сектора, s — длина дуги данного сектора, r — радиус круга.

Сегмент. Площадь сегмента

Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой. Любая хорда делит круг на два сегмента:

Площадь сегмента равна половине радиуса, умноженной на разность между дугой сегмента и половиной хорды двойной дуги.

Площадь сегмента AMB будет вычисляться по формуле:

где S — это площадь сегмента, r — радиус круга, s — длина дуги AB, а BC — длина половины хорды двойной дуги.

Источник

Сектор окружности формулы, описание и рисунки

Изучая плоские геометрические фигуры, необходимо четко понимать все определения того или иного обозначения. Правильное их представление позволит быстро и правильно освоить предлагаемые азы теории. И так окунемся в его мир.

• Часть круга, которая ограничена двумя радиусами и дугой окружности, проведенной из одной точки радиуса в другую, будем называть сектором.
• Часть круга, которая ограничена дугой окружности, проведенной из одной точки хорды в другую, будем называть сегментом.

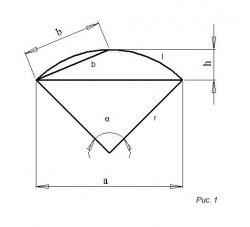
Сектор окружности и его сегмент изображены на 1-ом рисунке, где
r – радиус;
l – длина дуги;
a – хорда;
α – центральный угол (в градусах);
h – стрела сегмента;
S – площадь сектора;
S1 – площадь сегмента

a = 2√(2hr – h²) = 2r sin α/2
h = r – √(r² – a²/4) = r(1 – cos α/2) = a/2 tg α/4
l = 2πrα/360 ≈ 0.01745rα
S = πr²/360
S1 = r²/2 (2πα/180 – sin α) = ½ (lr – a(r – h))

Вспомогательные формулы
l ≈ 0,01745rα ≈ (8b – a)/3 ≈ √(a² + h²16/3)
S ≈ 0,00873r² α
S1 ≈ h/15(6a + 8b)

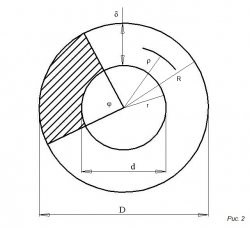
Круговое кольцо изображено на 2-ом рисунке, где
D – внутренний диаметр;
d – внешний диаметр;
R – внешний радиус;
R – внутренний ралиус;
ρ – средний радиус;
δ – толщина кольца;
S – площадь кольца;
S1 – площадь части кольца заштрихованной поверхности

D = 2R
d = 2r
ρ = ½(R + r)
δ = R – r
S = π(R² – r²) = π(D² – d²)/4 = 2πρδ
S1 = φπ(R² – r²)/360 = φπ(D² – d²)/180 = φπρδ/180

Надеемся, что полученная информация пригодится в решении различных задач и вопросов.

Источник

Геометрия. Урок 5. Окружность

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Определение окружности

Окружность – геометрическое место точек, равноудаленных от данной точки.

Отрезки в окружности

Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.

Хорда a – отрезок, соединяющий две точки на окружности.

Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).

O A – радиус, D E – хорда, B C – диаметр.

Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.

Касательная к окружности – прямая, имеющая с окружностью одну общую точку.

Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.

Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).

Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.

Дуга в окружности

Теорема 4:
Равные хорды стягивают равные дуги.

Углы в окружности

В окружности существует два типа углов: центральные и вписанные.

Центральный угол – угол, вершина которого лежит в центре окружности.

∠ A O B – центральный.

Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.

Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.

∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2

∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °

Длина окружности, длина дуги

Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.

Длина окружности находится по формуле:

Площадь круга и его частей

Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.

Круг – часть пространства, которая находится внутри окружности.

Иными словами, окружность – это граница, а круг – это то, что внутри.

Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.

Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.

Площадь круга находится по формуле: S = π R 2

Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Примеры сектора в реальной жизни: кусок пиццы, веер.

Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α

Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.

Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.

Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.

S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α

Теорема синусов

Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с окружностями.

Источник

Угол, образованный соединением концов дуги с любой точкой окружности, не входящей в сектор, равен половине центрального угла.

СОДЕРЖАНИЕ

использование

Традиционно направление ветра на компасной розетке задается одним из 8 октантов (N, NE, E, SE, S, SW, W, NW), потому что это более точно, чем просто указание одного из 4 квадрантов и флюгера. как правило, не имеет достаточной точности для более точной индикации.

Площадь

А знак равно ∫ 0 θ ∫ 0 р d S знак равно ∫ 0 θ ∫ 0 р р

знак равно ∫ 0 θ 1 2 р 2 d θ

Преобразование центрального угла в градусы дает

Периметр

Длина периметра сектора складывается из длины дуги и двух радиусов:

Длина дуги

Формула длины дуги:

где L представляет длину дуги, r представляет радиус круга, а θ представляет угол в радианах, образованный дугой в центре круга.

Если значение угла указано в градусах, то мы также можем использовать следующую формулу:

Длина хорды

Длина хорды, образованной экстремальными точками дуги, определяется выражением

где C представляет длину хорды, R представляет радиус круга, а θ представляет угловую ширину сектора в радианах.

Источник

Площадь круга и его частей. Длина окружности и ее дуг

Основные определения и свойства. Число π

Формулы для площади круга и его частей

Формулы для длины окружности и ее дуг

Площадь круга

Длина окружности

Длина дуги

Площадь сектора

Площадь сегмента

Основные определения и свойства

Часть окружности, расположенная между двумя точками окружности

Конечная часть плоскости, ограниченная окружностью

Часть круга, ограниченная двумя радиусами

Часть круга, ограниченная хордой

Выпуклый многоугольник, у которого все стороны равны и все углы равны

Около любого правильного многоугольника можно описать окружность

Фигура	Рисунок	Определения и свойства
Окружность
Дуга
Часть окружности, расположенная между двумя точками окружности
Круг
Конечная часть плоскости, ограниченная окружностью
Сектор
Часть круга, ограниченная двумя радиусами
Сегмент
Часть круга, ограниченная хордой
Правильный многоугольник
Выпуклый многоугольник, у которого все стороны равны и все углы равны Около любого правильного многоугольника можно описать окружность Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами. Формулы для площади круга и его частей , где R – радиус круга, D – диаметр круга , если величина угла α выражена в радианах , если величина угла α выражена в градусах , если величина угла α выражена в радианах , если величина угла α выражена в градусах , где R – радиус круга, D – диаметр круга Числовая характеристика Рисунок Формула Площадь круга Площадь сектора , если величина угла α выражена в радианах , если величина угла α выражена в градусах Площадь сегмента , если величина угла α выражена в радианах , если величина угла α выражена в градусах Формулы для длины окружности и её дуг где R – радиус круга, D – диаметр круга если величина угла α выражена в радианах , если величина угла α выражена в градусах где R – радиус круга, D – диаметр круга Числовая характеристика Рисунок Формула Длина окружности Длина дуги если величина угла α выражена в радианах , если величина угла α выражена в градусах Площадь круга Длина окружности откуда вытекает формула для длины окружности радиуса R : Длина дуги Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла. В случае, когда величина α выражена в градусах, справедлива пропорция из которой вытекает равенство: В случае, когда величина α выражена в радианах, справедлива пропорция из которой вытекает равенство: Площадь сектора В случае, когда величина α выражена в градусах, справедлива пропорция из которой вытекает равенство: В случае, когда величина α выражена в радианах, справедлива пропорция из которой вытекает равенство: Площадь сегмента Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла. Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем В случае, когда величина α выражена в в радианах, получаем Источник ← что такое идентификатор пользователя в сбербанк лесть это простыми словами что значит → Вам также понравится что такое ошибка 5831 06.12.202324.04.2022 admin 0 что такое бизнес омбудсмен 10.12.202316.04.2022 admin 0 Цетиловый спирт что это 04.12.202317.05.2022 admin 0 Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сохранить моё имя, email и адрес сайта в этом браузере для последующих моих комментариев.