что такое круглые и некруглые числа
Что такое круглые и некруглые числа
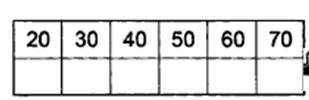
Разделите данные числа по какому-либо признаку (рис. 1).
Решение: 1. Разделим их на двузначные и трёхзначные числа (табл. 1).
Таблица 1. Двузначные и трёхзначные числа
Двузначные
Трёхзначные
2. Также данные числа можно разделить на круглые и некруглые числа (табл. 2).
Таблица 2. Круглые и некруглые числа
Круглые
Некруглые
При сложении и вычитании чисел, запись которых заканчивается нулями, всегда можно заменить их действиями с сотнями и десятками.
1.
2.
3.
4.
5.
6.
7.
8.
9.
Решение: 1. Заменим числа в первом примере на числа с сотнями:

2. Заменим исходные числа во втором примере на числа с сотнями:

3. Заменим число триста на тридцать десятков:

4. В четвёртом примере заменяем числа десятками:

5. Чтобы сложить числа в пятом примере, заменяем числа десятками:

6. В примере заменим числа десятками, и выполним вычисления:

7. Числа заменяем сотнями:
8. В восьмом примере тоже заменяем числа сотнями, а потом считаем:

9. Выполним замену чисел на десятки:

Витя купил 400 г сыра, а масла – на 100 г больше (схема 1, рис. 2, 3). Найди массу этой покупки.
Решение: 1. Вначале вычислим, сколько масла купил Витя.
2. Теперь определим общую массу покупки:
Решение: 1. В первом уравнении неизвестное – уменьшаемое. Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое.
Заменяем числа:

2. Во втором уравнении неизвестное число – слагаемое. Чтобы найти неизвестное слагаемое, надо от суммы отнять известное слагаемое.
Заменяем числа:
Список литературы
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
Домашнее задание
Круглые числа
Кру́глыми чи́слами относительно некоторой позиционной системы счисления называют степени её основания. В этой системе счисления такие числа записываются как единица с последующими нулями. Количество нулей справа от единицы равно показателю степени основания.
Примеры
Обобщения
Иногда понятие круглого числа расширяют до всех чисел, являющихся произведением базового числа (такого, которое можно записать одной цифрой) и степени основания, например, 400010=410 × 100010, 6000008=68 × 1000008, 203=23 × 103. В записи такого числа есть одна ненулевая цифра с левого края и несколько нулей справа от неё.
Ещё шире круглое число можно определять как всякое число кратное степени основания системы счисления, то есть достаточно присутствия одного или нескольких нулей с правого края, например, 45600010=45610 × 100010, 3405=345 × 105, 1001002 = 10012 × 1002. В такой трактовке понятия для любого составного числа с помощью факторизации можно найти систему счисления, в которой это число будет круглым. Например, число 3410 = 17 × 2 является круглым в любой системе счисления, основание которой равно одному из делителей числа. В данном случае 3410=1000102=2017.
Полезное
Смотреть что такое «Круглые числа» в других словарях:
Круглые числа всегда лгут — Слова английского писателя и лексикографа Сэмюэля Джонсона (1709 1784). Иносказательно: сомнение в истинности какой либо информации, подкрепленной подозрительно круглыми числами. Энциклопедический словарь крылатых слов и выражений. М.: «Локид… … Словарь крылатых слов и выражений
КЛАСС НЕМАТОДЫ или КРУГЛЫЕ ЧЕРВИ (NEMATODA) — Если бы тип немательминтов был ограничен только рассмотренными выше классами животных, то едва ли была бы построена та общая характеристика этого типа, которая возникла в современной науке. Кроме того, его значение и в экономике природы … Биологическая энциклопедия
Центрированные шестиугольные числа — – это центрированные фигурные числа, которые представляют шестиугольник с точкой в центре и все остальные окружающие точки находятся в шестиугольной решётке. 1 7 19 37 +1 +6 +12 +18 … Википедия
Список чисел — Содержание 1 Натуральные числа 1.1 от 1 до 2099 1.2 «Круглые» числа от 200 до 10000 1.3 Степени двойки … Википедия
Правила округления — Округление математическая операция, позволяющая уменьшить количество знаков в числе за счёт замены числа его приближённым значением с определённой точностью. Содержание 1 Методы округления 1.1 Варианты округления к ближайшему целому … Википедия
Круглое число — Круглыми числами относительно некоторой позиционной системы счисления называют степени её основания. В этой системе счисления такие числа записываются как единица с последующими нулями. Количество нулей справа от единицы равно показателю степени… … Википедия
Катерхэм (команда Формулы-1) — Caterham … Википедия
Рамануджан, Сриниваса Айенгор — Один из немногих известных портретов С. Рамануджана Рамануджан Сриниваса Айенгор (Ramanujan) (22 декабря 1887, Ироду на юге Индии, 26 апреля 1920, близ Мадраса) индийский математик. Не имея специального математического образования, получил… … Википедия
Рамануджан — Один из немногих известных портретов С. Рамануджана Рамануджан Сриниваса Айенгор (Ramanujan) (22 декабря 1887, Ироду на юге Индии, 26 апреля 1920, близ Мадраса) индийский математик. Не имея специального математического образования, получил… … Википедия
Рамануджан, Сриниваса — Один из немногих известных портретов С. Рамануджана Рамануджан Сриниваса Айенгор (Ramanujan) (22 декабря 1887, Ироду на юге Индии, 26 апреля 1920, близ Мадраса) индийский математик. Не имея специального математического образования, получил… … Википедия
Последовательность двузначных чисел
В первом классе изучали однозначные числа, изучение двузначных чисел проходит во втором классе.
Что такое двузначные числа?
Для начала дадим определение двузначного числа – это число, состоящее из двух знаков. Любое двузначное число является комбинацией двух однозначных чисел.
Все числа, а также и двузначные, изучаются на основе принципов письменное и устной нумерации десятичной системы исчисления.
Последовательность двузначных чисел
Изучение двузначных чисел больше 20, осуществляется в следующем порядке. Сначала мы на основе счета десятками предлагаем ознакомиться с ≪круглыми≫ двузначными числами.
Такие числа принято называть ≪круглыми≫ (≪полными≫) десятками. Изучим такие числа. Числа 10 и 20 нам уже известны с первого класса.
Так что продолжить эту последовательность в плане письменной нумерации не составит особого труда: записи чисел 30, 40, 50, 60, 70, 80, 90 возникают аналогично.
Сложнее разобраться с устной нумерацией. Если образование числительных, как тридцать, пятьдесят, шестьдесят, семьдесят, восемьдесят, можно объяснить составом этих слов (состоит из двух слов – три и десять, пять и десять и т.д.), то числа сорок и девяносто так не объяснить.
Эти числительные нужно запомнить, не пытаясь увидеть в них смысловую структуру. Также эти числительные могут и сыграть положительную роль в обучении.
Учитель может предложить учащимся одну из исторических версий возникновения этих числительных, и это явно сыграет положительную роль в развитии познавательного интереса учащихся.
Некруглые двузначные числа
Мы разобрали так называемые «круглые» двузначные числа. Также есть «некруглые» двузначные числа – это числа, находящиеся между «круглыми» (между 10 и 20, 20 и 30, 30 и 40 и так далее).
Устная и письменная нумерация «некруглых» двузначных чисел строится на разрядном принципе с учетом представления данного числа в виде суммы «круглого» двузначного числа и однозначного числа.
Разберем разрядный состав двухзначных чисел. Все двузначные числа состоят из разрядов. Круглые двузначные числа состоят из однозначного числа и 0, а некруглые из суммы круглого двузначного числа и однозначного числа.
Однозначные и двузначные числа. Круглые числа.



| Вспомни! Числа, в записи которых один знак (одна цифра) называются однозначными. Числа, в записи которых два знака называются двузначными. |
1. Разбей следующие числа на 2 группы: 16, 61, 5, 10, 8, 99, 1
2. Угадай по описанию числа
Двузначное число, при счёте его называют сразу же после числа 16.
Двузначное число, в нём 1 десяток и 5 единиц.
Наименьшее двузначное число.
Наибольшее двузначное число.
3. Распредели числа 10, 13, 55, 60, 23, 32, 30 на две группы, круглые числа и некруглые числа.
| Вспомни! Числа и числовые выражения можно сравнивать. Сравнить числовое выражение – найти значение каждого из выражений и их сравнить. |
Сложение и вычитание
5. Найди сумму чисел. Напиши, как можно прочитать выражения.
Образец: 5 + 3 = 8 – сумма чисел 5 и 3
— первое слагаемое 5, второе слагаемое 3
6. Найди разность чисел. Напиши, как можно прочитать выражения.
Образец: 5 – 2 = 3 – разность чисел 5 и 3
— уменьшаемое 5, вычитаемое 2
7. Выполни проверку.
| Вспомни! При решении примеров можно пользоваться правилом: От перестановки слагаемых сумма не меняется. Например, 5+3=8 3+5 =8 |
8. Выполни по образцу:
| Вспомни! Способы проверки вычитания Вычитание можно проверить вычитанием. Для этого надо из уменьшаемого (из целого) вычесть разность. Например:8 – 3 = 5 Проверка: 8 – 5 = 3 Вычитание можно проверить сложением. Для этого надо к разности прибавить вычитаемое (сложить две части). Например: 8 – 3 = 5 Проверка: 5 + 3 = 8 |
9. Выполни проверку двумя способами.
10. Найди неизвестное число.
| Вспомни! Иногда попадаются такие числовые выражения, которые нужно складывать или вычитать в столбик. Вспомни основные приёмы сложения и вычитания (смотри памятку). |
11. Реши примеры в строчку и в столбик:
*Данное задание выполни в тетради
| Вспомни! Приёмы вычислений пригождаются при решении задач. |
12. Реши задачи на нахождение суммы. Обязательно решение задачи записывай в столбик!

Наклеек с растениями – 33 шт.
б) Миша прочитал за 3 недели 13 книг, а Серёжа 26. Сколько всего книг прочитали мальчики за 3 недели?
*Данное задание выполни в тетради
13. Реши задачу на нахождение неизвестного cлагаемого. Обязательно записывай решение задачи в столбик!
Образец краткой записи: За два дня Аня съела 14 морковок. В первый день она съела 5 штук. Сколько морковок она съела во второй день?

За два дня Аня съела 14 конфет. В первый день она съела 5 штук. Сколько конфет она съела во второй день?
*Данное задание выполни в тетради
14. Вычисли и заполни таблицу
15. Реши задачи на нахождение неизвестного вычитаемого и слагаемого. Обязательно записывай решение задачи в столбик!
Образец: У Иры было 19 тетрадей. Когда несколько тетрадей Ира исписала, осталось 6. Сколько тетрадей исписала Ира?
19 – 6 = 13 (т.) Обрати внимание, вычитаем из целого!
Ответ: 13 тетрадей исписала Ира.
а) На полке стояло 25 книг. Когда на полку поставили ещё несколько книг, их стало 38. Сколько книг поставили на полку?
б) В магазине было 97 банок сгущённого молока. Когда несколько банок продали, осталось 24 банки. Сколько банок сгущённого молока продали?
*Данное задание выполни в тетради

17. Реши задачи на увеличение и уменьшение числа на несколько единиц. Обязательно записывай решение задачи в столбик!
| Вспомни!На – плюс/минус В – умножить/разделить |
Образец: В маленькой пирамидке 8 кружков, а в большой – на 3 кружка больше. Сколько кружков в двух пирамидках?
1) 8 + 3 = 11 (к.) – в большой пирамидке. ! Обрати внимание, что прибавляем к 8 (так как это число мы знали изначально)
Не забывай, что решение задачи можно записать одним выражением:
8 + (8+3) = 19 (п.), где 8 –количество кружков в маленькой пирамидке;
8+3 – данное выражение показывает количество кружков в большой пирамидке
Нужно найти, сколько всего кружков в дух пирамидках: и в маленькой пирамидке, и в большой.
а) В Московском поезде 17 вагонов, а в Тульском на 3 вагона меньше. Сколько вагонов в Московском и Тульском поездах вместе?
б) На арене цирка выступают 27 жонглёров, а акробатов – на 4 меньше. Сколько жонглёров и акробатов вместе выступает на арене цирка?
в) Максим решил 23 задачи, а Макар на 12 задач больше. Сколько всего задач решили мальчики вместе?
*Данное задание выполни в тетради
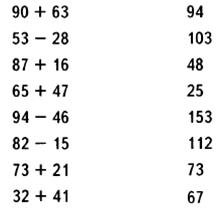
18. Соедини с верным ответом.
| 7. Вспомни! Чтобы узнать, на сколько одно число больше или меньше другого, надо из большего вычесть меньшее. 8. 9. На сколько 8 больше 5? 10. 8 – 5 = 3 11. Ответ: 8 больше 5 на 3. |
19. Ответь на вопросы.
На сколько 35 меньше, чем 78?
На сколько 67 меньше, чем 100?
На сколько 99 больше, чем 67?
20. Реши задачи на разностное сравнение. Обязательно записывай решение задачи в столбик!
а) В саду 34 куста малины и 15 кустов крыжовника. На сколько меньше кустов крыжовника, чем кустов малины?
б) Один арбуз весит 23 кг, а другой – 17 кг. На сколько первый арбуз тяжелее второго?
*Данное задание выполни в тетради
Умножение и деление
| Вспомни! Умножение – это сложение одинаковых слагаемых. 5 + 5 + 5 + 5… |
21. Замени сумму одинаковых слагаемых умножением.
Образец: 5 + 5 + 5 = 5·3 =15
7 + 7 + 7 = ___________________________________
9 + 9 + 9 + 9 = ________________________________
8 + 8 + 8 + 8 + 8 + 8 = ___________________________
4 + 4 + 4 + 4 + 4 + 4 = ____________________________
22. Замени умножение суммой одинаковых слагаемых.
Образец: 3· 4 = 3+ 3 + 3 + 3
3· 6 = ____________________________________________
6 · 4 = ___________________________________________
2 · 8 = ___________________________________________
23. Найди произведение чисел. Напиши, как можно прочитать выражения.
Образец: 5 · 3 = 15 – произведение чисел 5 и 3
— первый множитель 5, второй множитель 3
24. Найди частное чисел. Напиши, как можно прочитать выражения.
Образец: 15 : 3 = 5 – частное чисел 15 и 3
— делимое 15, делитель 3
| Вспомни! Деление – это обратное действие умножению. Так как умножение двух чисел можно проверить делением. 2·3=6 Чтобы узнать правильно ли было выполнено умножение, можно: · Разделить произведение на первый множитель. Если получится второй множитель, то умножение выполнено верно: 6:2 =3 · Разделить произведение на второй множитель. Если получится первый множитель, то умножение выполнено верно: 6:3 =2 |
25. Выполни проверку.
| Вспомни! При решении примеров можно пользоваться правилом: От перестановки множителей произведение не меняется Например, 5· 3=15 и 3· 5 = 15 |
26. Выполни по образцу:
3· 5 = 15 ____________ ____________
15:3 = 5 ____________ _____________
15:5 =3 ____________ _____________
| Вспомни! Способы проверки деления Деление можно проверить делением. Для этого делимое (целое) нужно разделить на частное. Например: 15:3 = 5 Проверка: 15:5 =3 Деление можно проверить умножением. Для этого надо частное умножить на делитель Например: 15:3=5 Проверка: 5·3=15 |
27. Выполни проверку двумя способами.
28. Найди неизвестное число.
| Вспомни! Особые случаи умножения При умножении любого числа на 0 получится 0: 2 · 0 = 0 При умножении любого числа на 1 получится то же самое число: 2 · 1 = 2 |
| Вспомни! Особые случаи деления При делении числа на себя получается 1: 2:2 =1 При делении числа на 1 получается то же самое число: 2:1 =2 При делении нуля на любое число, получится 0: 0:5 = 0 Делить на 0 нельзя! |
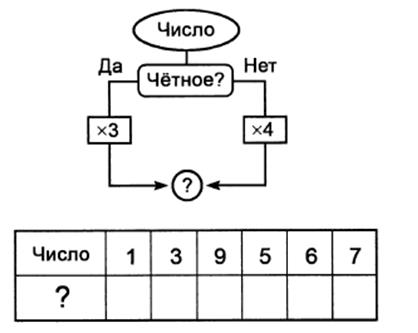
| Вспомни! Числа, которые делятся на 2, называют чётными. 2, 4, 6, 8, 10… Числа, которые не делятся на 2, называют нечётными. 1, 3, 5, 7, 9, 11… |
| Вспомни!Знание таблицы умножения тебе поможет в решении задач. |
32. Реши простые задачи на умножение.
Образец: Сколько колёс у трёх двухколесных велосипедов?
Ответ: 6 колёс у трёх двухколесных велосипедов.
. Обрати внимание! Ищем количество колёс, поэтому количество колёс (2) ставим на первое место.
Или можно решить задачу сначала с помощью сложения: 2 + 2 + 2 =6, а потом сложение заменить умножением: 2 · 3 = 6
а) В магазин привезли 2 коробки сухофруктов по 7 кг в каждой. Сколько килограммов сухофруктов привезли в магазин?
б) В одной вазе 7 цветков. Сколько цветков в 3 таких же вазах?
*Данное задание выполни в тетради
33. Зачеркни выражения, решённые неверно:
34. Реши задачи на увеличение и уменьшение числа в несколько раз.
Образец: а) У Сережи 4 солдатика, а у Антона в 2 раза больше. Сколько солдатиков у Антона?

а) У Серёжи 4 солдатика, а у Антона в 2 раза больше. Сколько солдатиков у Антона?
б) У Серёжи 4 солдатика, а у Антона в 3 раза больше. Сколько солдатиков у двух мальчиков?
(по действиям + одним выражением)
в) В кружках занималось 18 мальчиков, а девочек в 2 раза меньше. Сколько девочек занималось в кружке?
г) В кружках занималось 18 мальчиков, а девочек в 2 раза меньше. Сколько всего детей занималось в кружке? (по действиям + одним выражением)
*Данное задание выполни в тетради
| Вспомни!Примеры можно объединять в выражения! 1) 5 + 4 = 9 2) 9 – 2 = 7 (5+ 4) – 2 = 7 Смотрим на второй пример! Число 9 мы находили в первом примере. или 1) 4 + 6 = 10 2) 7 + 10 = 17 7 + (4+6) = 17 |
35. Объедини примеры в одно выражение: