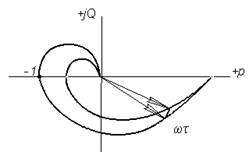
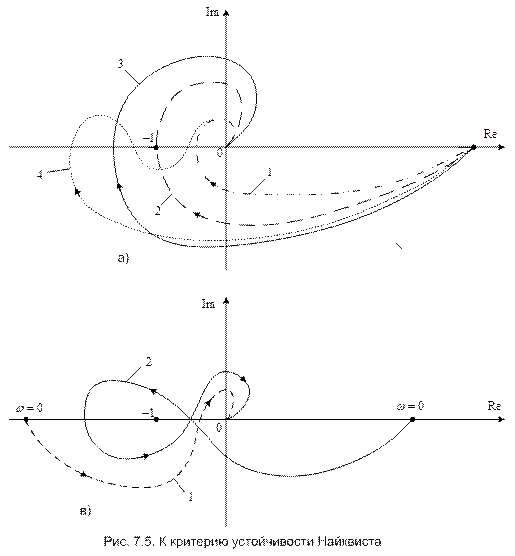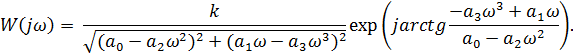что такое критерий найквиста

Критерий устойчивости Найквиста

Этот критерий, предложенный в 1932 г. американским ученым Г. Найквистом, позволяет судить об устойчивости замкнутой системы по амплитудно-фазовой частотной характеристикеке (АФЧХ) 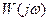разомкнутой системы (рис. 7.5).

Рассмотрим сначала случай 1, когда известно, что система в разомкнутом состоянии устойчива (рис. 7.5, а). Условие устойчивости замкнутой системы тогда сводится к требованию, чтобы АФЧХ разомкнутой системы не охватывала точку (-1, j0). На рис. 7.5, а характеристики 1 и 4 соответствуют устойчивым системам, характеристика 3 – неустойчивой, а характеристика 2 – нахождению системы на границе устойчивости.

Если, например, уменьшать коэффициент передачи в неустойчивой системе, ее АФЧХ будет сжиматься к началу координат, в результате чего система станет в конце концов устойчивой. Наоборот, при увеличении коэффициента передачи характеристика ранее устойчивой системы в конце концов охватит точку (-1, j0), и система потеряет устойчивость.

Для случая 2, т.е. для систем, неустойчивых в разомкнутом состоянии, критерий Найквиста имеет такую формулировку: для устойчивости системы в замкнутом состоянии АФЧХ разомкнутой системы должна охватывать точку (-1, j0). При этом число пересечений ею отрицательной действительной полуоси левее точки (-1, j0) сверху вниз должно быть на k/2 больше числа пересечений в обратном направлении, где k – число правых полюсов передаточной функции W(s) разомкнутой системы, т.е. число полюсов с положительной действительной частью.

На рис. 7.5, в в качестве примера показаны две АФЧХ разомкнутой системы, неустойчивой в разомкнутом состоянии вследствие наличия правых корней, но устойчивой в замкнутом состоянии. Характеристика 1 соответствует k = 1, а характеристика 2 – значению k = 2. (В первом случае имеем «половину» пересечения действительной оси левее точки (-1, j0)).

Таким образом, в общем случае при применении критерия Найквиста необходимо предварительно определить число правых полюсов W(s). Для одноконтурной системы, когда знаменатель W(s) представляет собой произведение знаменателей передаточных функций отдельных звеньев, это число находится легко, поскольку полюсами W(s) являются полюсы передаточных функций отдельных звеньев.

У многоконтурных систем, особенно с перекрестными связями, задача определения числа k усложняется, и поэтому в этих случаях целесообразно отказаться от применения критерия Найквиста. В соответствии с критерием Найквиста об устойчивости можно судить не только по АФЧХ, но и совместно по АЧХ и ФЧХ разомкнутой системы. Обычно при этом пользуются логарифмическими характеристиками, что представляет большое удобство в силу простоты их построения.

Согласно критерию Найквиста, для системы, устойчивой в разомкнутом состоянии, условием устойчивости ее в замкнутом состоянии является неохват АФЧХ 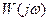точки (-1, j0). Последнее имеет место, если при частоте, на которой А(ω) = 1, абсолютное значение фазы меньше π.

Сказанное непосредственно следует из рис. 7.5, а.

Таким образом, применительно к логарифмическим характеристикам, если учесть при этом, что значению А = 1 соответствует L = 20 lg A = 0, критерий устойчивости Найквиста для систем, устойчивых в разомкнутом состоянии, сводится к тому, что ЛАХ должна пересечь ось абсцисс раньше, чем фаза, спадая, окончательно перейдет за значение – π. Или иными словами: на частоте среза ω_с величина фазы должна быть меньше π.

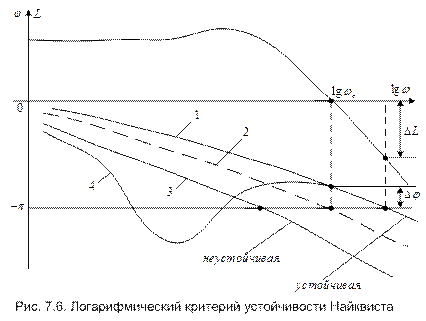
Изложенное иллюстрируется на рис. 7.6.

Здесь изображены ЛАХ L(ω) и четыре варианта ЛФХ φ(ω). В случае ЛФХ 1 и 4 замкнутая система устойчива, причем характеристика 4 соответствует АФЧХ 4 на рис. 7.5, а. ЛФХ 2 соответствует нахождению замкнутой системы на границе устойчивости, ЛФХ 3 – неустойчивой замкнутой системе.

Для систем, неустойчивых в разомкнутом состоянии, требования к ЛАХ и ЛФХ в отношении устойчивости можно сформулировать, исходя из соответствующих требований к АФЧХ. В частности, для систем, неустойчивых в разомкнутом состоянии, условием устойчивости в замкнутом состоянии является следующее: при положительной ЛАХ число пересечений ЛФХ уровня – π снизу вверх должно быть на k/2 раз больше числа пересечений в обратном направлении.

При оценке устойчивости систем одного факта устойчивости недостаточно. Необходимо еще оценить величину запаса устойчивости, т.е. степени удаленности системы от границы устойчивости. Система, которая теоретически является устойчивой, но находится очень близко к границе устойчивости, практически при ее реализации может оказаться неустойчивой как вследствие неточности математического описания системы, использованного при оценке устойчивости, так и из-за изменения во времени параметров системы.

В случае применения критерия Рауса-Гурвица о запасе устойчивости можно судить по тому запасу, с которым выполняются входящие в этот критерий неравенства. При использовании графических критериев Михайлова и Найквиста запас устойчивости определяется удаленностью соответствующих характеристик от критического положения, при котором система находится на границе устойчивости. Для критерия Михайлова это будет удаленность годографа D(jω) от начала координат, а для критерия Найквиста – удаленность характеристики W(jω) от точки (-1, j0).

Основное распространение в качестве меры запаса устойчивости получили вытекающие из критерия Найквиста две величины – запас устойчивости по фазе Δφ и запас устойчивости по амплитуде ΔL. Эти величины показаны на рис. 7.6 для системы с ЛФХ, представленной кривой 1. Аналогично они могут быть найдены и по АФЧХ.

Запас устойчивости по фазе определяется величиной Δφ, на которую должно возрасти запаздывание по фазе в системе на частоте среза ω_с, чтобы система оказалась на границе устойчивости.

Запас устойчивости по амплитуде определяется величиной ΔL допустимого подъема ЛАХ, при котором система окажется на границе устойчивости. Таким образом, запас по амплитуде представляет собой запас по коэффициенту передачи k разомкнутой системы по отношению к его критическому по устойчивости значению.

Рассмотренные критерии устойчивости тем или иным способом оценивают один и тот же факт: имеются ли среди корней характеристического уравнения замкнутой системы корни с положительной вещественной частью. Поэтому все они дают одинаковый результат в оценке устойчивости системы.

Надо отметить, что прежде чем исследовать устойчивость САУ с помощью того или иного критерия, следует убедиться, что необходимое условие устойчивости выполняется, т.е. все коэффициенты характеристического уравнения системы являются положительными числами.

Каждый из критериев применяют в зависимости от того, какими исходными характеристиками и данными располагают. Если известны дифференциальные уравнения системы, то чаще применяют алгебраические критерии устойчивости.

Достоинством алгебраических критериев является сравнительная простота применения, а недостатком – то, что они не позволяют оценить влияние на устойчивость системы параметров отдельных ее элементов. Этого недостатка лишен графоаналитический критерий Михайлова.

Чтобы с помощью критерия Михайлова оценить влияние изменения параметров элементов системы на ее устойчивость, необходимо построить кривую Михайлова при заданном значении интересующего нас параметра. А потом изменять этот параметр и смотреть, как будет меняться кривая Михайлова.

При известной АФЧХ используют частотный критерий Найквиста. С помощью этого критерия также можно оценить влияние параметров элементов системы на ее устойчивость. АФЧХ можно снять экспериментально.

Оценка устойчивости автоматической системы по ее структуре.

В ряде случаев оценить устойчивость автоматической системы можно по ее структуре. Это значительно сокращает время, так как нет необходимости составлять характеристическое уравнение.

Если система имеет такую структуру, что в ней невозможно обеспечить устойчивость ни при каком значении ее элементов, то такая система называется структурно-неустойчивой.

Оценим устойчивость данной системы по ее структуре. Например, если система имеет два интегрирующих звена, не охваченных жесткой обратной связью, и не имеет последовательно включенных дифференцирующих звеньев, то она будет неустойчивой при любом значении параметров ее элементов.

Покажем это на примере простейшей системы, состоящей из одного апериодического и двух интегрирующих звеньев. Передаточная функция такой системы в разомкнутом состоянии

,

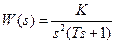
а характеристическое уравнение замкнутой системы

.

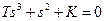
Для этого уравнения не выполняется необходимое условие устойчивости. Следовательно, система будет неустойчива при любых значениях параметров Т и К, т.е. она будет структурно-неустойчивой.

Структурно-неустойчивую систему можно превратить в устойчивую только изменением ее структуры, т.е. введением дополнительных элементов, например, дифференцирующих элементов при включении пропорциональных элементов параллельно интегрирующим.

Запас устойчивости САУ.

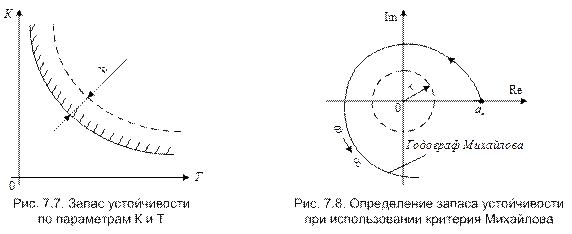
Запас устойчивости – это количественная оценка отклонения значений параметров системы или ее характеристик от зоны, опасной с точки зрения устойчивости. Запас устойчивости по параметрам характеризует расстояние граничной кривой, определяющей область разрешенных значений параметров, от границы области устойчивости. На рис. 7.7 запас устойчивости по параметрам Т и К обозначен через h.

Запас устойчивости по критерию Михайлова равен радиусу окружности r, в которую не должна заходить кривая Михайлова (рис. 7.8). Центром окружности является «опасная» точка при применении критерия Михайлова, т.е. начало координат.

Источник

Что такое критерий найквиста

Рисунок 3. К критерию Ляпунова: x _i –

корни характеристического уравнения

Необходимым и достаточным условием устойчивости линейной системы является условие, когда все вещественные корни характеристического уравнения системы, а также действительные части комплексных корней, отрицательны. Если один из корней положителен – система неустойчива; если равен 0 – система находится на границе устойчивости (рис. 3). Мнимая ось является границей устойчивости.

Однако пользоваться этим условием на практике для оценки устойчивости реальных систем оказывается достаточно сложно, так как реальные промышленные системы описываются дифференциальными уравнениями высокого порядка, или содержат звенья чистого запаздывания, так что нахождение корней характеристического уравнения представляет трудную задачу.

Алгебраический критерий устойчивости (Критерий Рауса-Гурвица ) является наиболее распространенным алгебраическим критерием и применяется для определения устойчивости системы, когда известно характеристическое уравнение. Характеристическое уравнение – знаменатель передаточной функции.

Пусть характеристическое уравнение системы имеет вид

Достаточное условие устойчивости:

Вывод. Все условия выполнены, система устойчива.

Частотный критерий Михайлова так же, как и алгебраический критерий, применяется в тех случаях, когда задано характеристическое уравнение системы:

Обозначим полином, стоящий в левой части характеристического уравнения, через D ( p ), т.е.

При изменении w от 0 до ¥ вектор D ( j w ) опишет кривую, называемую годограф Михайлова.

Формулировка критерия. Система устойчива, если годограф Михайлова при изменении частоты от 0 до ¥ начинается на положительной части действительной оси комплексной плоскости, проходит последовательно против часовой стрелки n квадрантов плоскости, нигде не обращается в 0 и не проходит через начало координат ( n – порядок характеристического уравнения системы). Если годограф проходит через начало координат комплексной плоскости, то система находится на границе устойчивости, если нарушается, хотя бы одно из условий критерия – система неустойчива. На рис. 4 приведены примеры годографов Михайлова D ( j w ).

Источник

Критерий устойчивости Найквиста

И Найквиста.

С помощью этих критериев исследуется устойчивость САР в частотой области.

Частотный критерий Михайлова

Исходная информация – характеристическое уравнение разомкнутой или замкнутой системы

Путём замены s на jw переходим к уравнению Михайлов

где Р(w) – вещественная часть годографа Михайлова, чётная функция частоты; Q (w) – мнимая часть годографа Михайлова, нечётная функция частоты.

Критерий Михайлова формулируется следующим образом: система устойчива, если годограф Михайлова при изменении w от 0 до ¥ проходит в положительном направлении n квадрантов комплексной плоскости, начиная свое движение с точки а₀ положительной полуоси, и нигде не обращается в нуль.

Критерий Михайлова имеет и другую формулировку: система устойчива, если действительная и мнимая части годографа Михайлова обращаются в нуль поочерёдно, т.е. если корни уравнений

действительные и перемежаются, при w = 0 P(0) > 0, Q(0) > 0.

Пример: определить устойчивость системы, характеристическое уравнение которой

D(p) = 0,0057s 3 + 0,58s 2 + s + 70.

Выполним подстановку s = jw и выделим вещественную и мнимую части годографа Михайлова

Для ряда значений частоты w вычислим вещественную

мнимую части кривой Михайлова

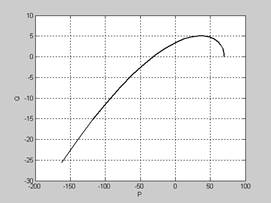
и результаты расчётов сведём в таблицу, по данным которой можно построить кривую Михайлова. Для определения точек пересечения осей нужно решить уравнения Р(ω) = 0 и Q(ω) = 0. Однако целесообразно для построения графика использовать возможности MATLAB:

Кривая Михайлова последовательно проходит три квадранта. Так как характеристическое уравнение исследуемой системы третьего порядка, то система устойчива.

Различные виды годографов представлены на рис. 6.4. Системе, находящейся на границе устойчивости, соответствует годограф, проходящий через начало координат, неустойчивой системе – кривая, проходящая через 1, 4 и 3 квадранты.

Критерий устойчивости Найквиста

Это также частотный критерий, позволяющий судить об устойчивости системы, замкнутой единичной отрицательной обратной связью, по амплитудно-фазовой частотной характеристике разомкнутого контура. Предварительно требуется исследование устойчивости разомкнутой системы, как правило, по алгебраическим критериям. Для устойчивых и неустойчивых в разомкнутом состоянии систем формулировки критерия разные.

Для систем, неустойчивых в разомкнутых состояниях, критерий Найквиста имеет такую формулировку: если разомкнутая система неустойчива и имеет m корней в правой полуплоскости, то для устойчивости в замкнутом состоянии необходимо и достаточно, чтобы амплитудно-фазовая характеристика разомкнутого контура охватывала точку с координатами (-1, j0) m/2 раз.

Если система имеет местные обратные связи, то необходимо проверить устойчивость внутренних контуров любым критерием.

Пример: задана передаточная функция системы управления

Исследовать её на устойчивость.

Сделаем замену s = jω и найдём АФЧХ:

Диаграмма Найквиста может быть построена в MATLAB с помощью функции nyquist([…],[…]) или nyquist(W).

Пример: построить годограф Найквиста для системы с передаточной функцией

В соответствии с критерием Гурвица эта система устойчива в разомкнутом состоянии. Исследуем её устойчивость в замкнутом состоянии:

>> nyquist([5],[1 3 3 1]) – рис. 6.5

АФЧХ разомкнутой системы не охватывает точку с координатами

(-1, j0), поэтому замкнутая система устойчива.

6.4. Устойчивость систем с запаздыванием.

Отдельные звенья САР обладают “чистым” запаздыванием, которое сказывается в том, что система реагирует на входной сигнал не сразу, а по истечении некоторого постоянного времени t. Это обстоятельство учитывается введением звена чистого запаздывания с передаточной функцией

а структурная схема системы показана на рис. 6.6.

Передаточная функция разомкнутой системы

Система без запаздывания (t = 0) называется предельной.

Частотные характеристики системы с запаздыванием и без него определяются, соответственно, выражениями

Отсюда видно, что для построения частотного годографа системы с запаздыванием следует построить годограф системы без запаздывания (предельной системы) и каждый вектор этого годографа повернуть по часовой стрелке на угол wt. Последний возрастает как при увеличении w, так и t.

Для некоторого значения t = t₀ и w = w_p годограф пройдёт через точку (-1, j0), и, следовательно, АСР будет находиться на границе устойчивости (рис. 6.7). Значения t₀ и w_p определяются из уравнения

Пример: система состоит из апериодического звена первого порядка с передаточным коэффициентом к > 1, постоянной времени Т и звена запаздывания с постоянной времени t. Определить предельное время запаздывания t₀, при котором система устойчива.

Источник

4. Критерий устойчивости Найквиста

Критерий был сформулирован в 1932 г. американским физиком X. Найквистом, занимавшимся исследованием свойств электронных усилителей с обратной связью. Позднее А.В. Михайлов обосновал этот критерий и показал возможность применения его для анализа автоматических систем управления.

В отличие от критериев Гурвица, Рауса и Михайлова, которые основаны на анализе характеристического уравнения системы, критерий Найквиста позволяет судить об устойчивости системы по амплитудно-фазовой характеристике разомкнутого контура системы. В этом заключается существенное преимущество критерия, так как построение амплитудно-фазовой характеристики разомкнутого контура для большинства реальных систем оказывается проще, чем построение годографа Михайлова. Особенно упрощается это построение для одноконтурных систем, состоящих из типовых звеньев. А в тех случаях, когда неизвестно математическое описание одного или нескольких конструктивных элементов системы и оценка их свойств возможна только путем экспериментального определения частотных характеристик, критерий Найквиста является единственно пригодным.

Основная формулировка критерия Найквиста:

автоматическая система управления устойчива, если амплитудно-фазовая характеристика W(j) разомкнутого контура не охватывает точку с координатами (–1; j0). Эта формулировка справедлива для систем, которые в разомкнутом состоянии устойчивы. Таковыми являются большинство реальных систем, состоящих из устойчивых элементов.

На рисунке 4.3, а изображены амплитудно-фазовые характеристики разомкнутого контура, соответствующие трем различным случаям: система устойчива (кривая 1); система находится на колебательной границе устойчивости (кривая 2); система неустойчива (кривая 3).

Употребленное в формулировке критерия Найквиста понятие охвата точки имеет некоторую неопределенность, из-за чего в случаях сложной формы кривой W(j) могут возникнуть затруднения в суждении об устойчивости системы. Поэтому для большей ясности рекомендуется следующий прием. Надо проследить мысленно за движением вектора W₁(j)=1+W(j), вращающегося вокруг точки (–1; j0) и скользящего по кривой W(j). Угол поворота вектора W(j), равный , означает охват точки (–1; j0), а угол, меньший  — не охват.

Для использования изложенного приема применительно к астатическим системам, которые содержат интегрирующее звено, и амплитудно-фазовые характеристики которых начинаются в – на мнимой оси, характеристику W(j) предварительно дополняют в четвертом квадранте дугой окружности бесконечно большого радиуса.

Для суждения об устойчивости систем, имеющих АФХ сложной конфигурации, когда кривая АФХ пересекает действительную ось левее точки (–1; j0) несколько раз, можно также использовать правило переходов, сформулированное советским ученым Я. 3. Цыпкиным: АФХ не охватывает точку (–1; j0), т.е. система устойчива, если при возрастании  разность между числом положительных (сверху вниз) и отрицательных (снизу вверх) переходов АФХ через ось абсцисс слева от точки (–1; j0) равна нулю.

Если АФХ начинается или заканчивается на отрезке (–;–1), то считают, что характеристика совершает полперехода. Частота, при которой амплитудная характеристика А() [модуль функции W(j)] принимает значение 1, называется частотой среза и обозначается _ср. Частоту, при которой фазовый сдвиг ()= –, обозначают _.

Пользуясь введенными обозначениями, можно записать условие нахождения системы на границе устойчивости:

Частота, с которой система колеблется на границе устойчивости, называется критической и обозначается _кр.

Физическая трактовка основной формулировки критерия Найквиста. Предположим, что на входе системы (рисунок 4.3, б) действует гармонический сигнал u(t)=u_msint с малой амплитудой u_m. Пусть частота  равна частоте _, при которой фазовый сдвиг (), создаваемый звеном W(j), равен –. Тогда сигнал обратной связи окажется в фазе с сигналом u(t), и мгновенные значения сигналов будут суммироваться.

Если на частоте =_ модуль |W(j_)|=1, т.е. выполняется условие (5.21), то в контуре системы будут поддерживаться незатухающие колебания даже после исчезновения внешнего воздействия u(t), т.е. система будет находиться на границе устойчивости. Характеристика W(j) при этом проходит через точку (–1; j0). Если на частоте =_ модуль |W(j_)| 1, то амплитуда сигналов в контуре будет неограниченно возрастать, т. е. система будет неустойчивой. Характеристика W(j) в этом случае охватит точку (–1; j0).

Таким образом, особая роль точки (–1; j0) заключается в том, что она, во-первых, соответствует превращению отрицательной обратной связи в положительную, и во-вторых, является граничной между режимами усиления и ослабления сигналов звеном W(j).

Иногда на практике встречаются системы, в контуре которых имеется один или несколько неустойчивых элементов. Такие системы в разомкнутом состоянии неустойчивы. Для суждения об их устойчивости необходимо использовать другую формулировку критерия Найквиста:

автоматическая система управления устойчива, если амплитудно-фазовая характеристика W(j) разомкнутого контура охватывает l/2 раз точку с координатами (–1; j0), где l — число правых корней характеристического уравнения разомкнутого контура.

Количество охватов при этом можно определять по правилу Цыпкина как разность между числом положительных и отрицательных переходов.

Данная формулировка критерия Найквиста является более общей, чем предыдущая. Действительно, если разомкнутая система устойчива (т.е. l=0), то для устойчивости замкнутой системы АФХ W(j) должна точку (–1; j0) охватывать нуль раз, т.е. не охватывать.

Из обеих формулировок следует, что для суждения об устойчивости системы необходимо предварительно установить устойчивость ее в разомкнутом состоянии. Обычно эта вспомогательная задача решается сравнительно легко, при помощи критерия Гурвица: для этого приравнивают к нулю знаменатель передаточной функции W(s) разомкнутого контура и анализируют данное характеристическое уравнение.

Во многих практических случаях устойчивость разомкнутого контура может быть оценена без каких-либо вычислений непосредственно по виду входящих в контур звеньев.

Критерий Найквиста удобно использовать для анализа устойчивости систем, содержащих звено запаздывания. Если звено запаздывания включено последовательно с остальными звеньями (рисунок 4.4, а), то амплитудно-фазовая функция разомкнутого контура может быть представлена как произведение

где W(j) — эквивалентная амплитудно-фазовая функция остальных звеньев.

Характеристику W(j) строят следующим образом. Вначале строят кривую W(j), а затем каждый вектор, соответствующий частоте _i поворачивают на угол _i (рисунок 4.4, б).

структура системы (а); АФХ разомкнутого контура (б)

Звенья запаздывания, как правило, ухудшают устойчивость систем.

Если разомкнутый контур системы образован последовательным соединением типовых динамических звеньев, то целесообразно частотную характеристику контура строить в логарифмической системе координат и об устойчивости системы судить по виду этой характеристики. При этом используют разновидность основной формулировки критерия Найквиста: система устойчива, если при достижении фазовой частотной характеристикой значения –180° логарифмическая амплитудная характеристика будет отрицательной (рисунок 4.5, кривые 1). Действительно, если L ()

Логарифмические частотные характеристики L() и () разомкнутого контура находят суммированием ординат соответствующих характеристик отдельных звеньев. Фазовые характеристики отдельных звеньев строят либо по нескольким вычисленным точкам, либо при помощи специальных шаблонов. Амплитудные характеристики отдельных звеньев строят приближенно в виде совокупности прямолинейных отрезков, по правилам, изложенным в разделе 3.

Критерий Найквиста, применяемый в логарифмической системе координат, часто называют логарифмическим критерием.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник