что такое кратность корня характеристического уравнения
Портал ТОЭ
6.2 Классический метод расчёта переходных процессов
где i ( t ) – переходный ток.
Дифференцированием приводим это уравнение к неоднородному дифференциальному уравнению 2-го порядка:
Порядок дифференциального уравнения определяется числом накопителей энергии в цепи.
Решение дифференциального уравнения:
где i пр ( t ) – частное решение неоднородного уравнения, принуждённая составляющая, ток в установившемся режиме, когда переходный процесс закончен (при t = ∞ );
i св ( t ) – общее решение однородного уравнения, свободная составляющая, ток во время переходного процесса, возникающий вследствие изменения электрических и магнитных полей.
Расчёт принуждённой составляющей сводится к расчёту по известным методам установившегося значения искомой величины в схеме после коммутации.
Если характеристическое уравнение
Корню p k кратности m k ≥ 1 соответствует слагаемое свободной составляющей вида
Составление характеристического уравнения
Корни характеристического уравнения – собственные частоты цепи, т.к. они определяют характер свободных процессов.
Степень характеристического уравнения может быть определена по электрической схеме без составления уравнения: она равна числу основных независимых начальных условий в послекоммутационной схеме после максимального её упрощения и не зависит от числа ЭДС в схеме.
Упрощение заключается в том, что последовательно и параллельно соединённые реактивные элементы должны быть заменены эквивалентными.
Случай наличия кратных корней характеристического уравнения.



ЛИНЕЙНЫЕ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
I. МЕТОД ЭЙЛЕРА
211. Предварительные замечания. В этой главе мы будем изучать линейные системы уравнений:
Где коэффициенты akl=(k, l=1,2,…,n) – постоянные вещественные числа, а fk(x) (k=1,2,…,n) – функции от х, непрерывные в интервале (a,b).
Применяя общую теорию линейных систем уравнений, изложенную в предыдущей главе, мы покажем, что система (1) всегда может быть проинтегрирована в конечном виде, т. е. либо в элементар- ных функциях, либо в квадратурах.
Так как интегрирование неоднородной линейной системы приводится к интегрированию соответствующей однородной системы, то рассмотрим сначала вопрос о построении общего решения однородной системы:
В силу теоремы о построении общего решения, для построения общего решения системы (2) достаточно построить хоть одну фундаментальную систему решений.
Применяя теорему о существовании фундаментальной системы решений, мы видим, что существует фундаментальная система решений, определенных и непрерывных в промежутке
Более того, согласно замечанию теоремы о существовании фундаментальной системы решений, существует фундаментальная система решений, голоморфных в интервале 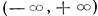
Мы покажем, что фундаментальная система решений может быть построена из элементарных функций, голоморфных в интервале 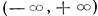
212. Построение фундаментальной системы решений и общего решения однородной линейной системы в случае различных корней характеристического уравнения. По аналогии с однородным линейным уравнением с постоянными коэффициентами будем искать частное решение системы (2) в виде
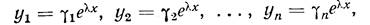
Обратим особое внимание на то, что число lмы берем одно и то же для всех функций, составляющих решение.
Подставляя функции (3) в систему (2), сокращая на е l x и пере- нося все члены направо, получим для определения чисел gk следующую систему:
Нас интересует ненулевое решение этой системы. Такое решение существует лишь при условии, что определитель системы равен нулю, т. е. при условии
Уравнение (5) называется характеристическим уравнением системы
Рассмотрим сначала случай, когда все характеристические числа
l1,l2. ln различны. В этом случае имеем: D(li)=0, но 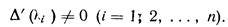
Составленной из коэффициентов системы
Действительно, вычисляя D’(l), имеем:
Поэтому одно из уравнений системы (7) есть следствие осталь-ных и эта система имеет ненулевое решение, определенное с точ-ностью до произвольного множителя пропорциональности Ai:
Например, в качестве gik можно взять алгебраические дополнения элементов любой строки определителя Dl(li), если не все они равны нулю. В самом деле, так как сумма произведений элементов какой-либо строки определителя Dl(li) на алгебраические дополнения эле-ментов другой строки равна нулю, а сумма произведений элементов строки на их алгебраические дополнения равна самому определителю D(li)т. е. снова равна нулю, то ясно, что, заменив в системе (7) неизвестные gk взятыми алгебраическими дополнениями, мы получим тождества.
Фиксируя в формулах (9) множитель Ai, мы получим определен-ное решение системы (7).
Эти решения линейно независимы в интервале 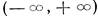
Если при этом все корни l1, l2. ln вещественны, то все решения (10) тоже будут вещественными.
Таким образом, в случае различных вещественных корней характеристического уравнения система (2) имеет п вещественных линейно независимых частных решений вида (10), так что последние образуют фундаментальную систему решений.
Поэтому, в силу теоремы о построении общего решения,формулы
Дают общее решение системы (2) в области
Если характеристические числа различные, но среди них есть комплексные,то последние входят сопряженными парами. Пусть a + ib и а – ib — простые корни характеристического уравнения. Корню a+ib соответствует согласно формуле (3) решение
Это решение комплексное. Отделяя в нем вещественные и мнимые части, мы получим, согласно свойствам решений однородной системы,два вещественных решения:
Эти решения, очевидно, линейно независимы в интервале 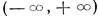
Таким образом, если все характеристические числа — различные и вещественные, то мы получаем соответствующие им вещественные линейно независимые частные решения в виде (10). Если же все характеристические числа — различные, но среди них есть комплексные, то последние обязательно входят сопряженными парами и каждой паре таких характеристических чисел соответствуют два линейно независимых частных решения вида (15). Всего мы получим п вещественных частных решений. Все эти решения линейно независимы в интервале 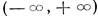
Общее решение системы (2) в области (12) представляет собою линейные комбинации построенных п вещественных линейно независимых частных решений с произвольными постоянными коэффициентами.
Пример 1. Найти общее решение системы:
Решая характеристическое уравнение
находим: l1=1, l2=9, так что характеристические числа различные и вещественные.
Составляем систему для определения чисел g1 и g2соответствующих характеристическому числу l1 = 1. Матрица коэффициентов этой системы получается из матрицы


4 5-l заменой l на l1=1, так что искомая система будет иметь вид
Таким образом, характеристическому числу Х1=1 соответствует решение:
Аналогично, решая систему, соответствующую характеристическому числу l2=9:
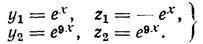
находим: g1=1, g2=1 так что этому характеристическому числу соот-ветствует решение:
Мы получили фундаментальную систему решений:
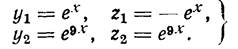
Беря линейную комбинацию, получаем общее решение:
Пример 2. Рассмотрим систему:
Это решение комплексное. Отделяя в нем вещественные и мнимые части, получим два вещественных решения
Эти решения составляют фундаментальную систему решений, так что общим решением будет
Пример 3. Найти общее решение системы:
Имеет различные и притом вещественные корни λ1 = 2, λ2 = 3, λ3=6, так что фундаментальная система решений имеет вид (10). Найдем сначала частное решение вида
который получается из характеристического определителя Δ (λ) заменой λ на λ1=2. Получаем
Подставляя эти значения γ1k в (33), получим
Так что общее решение имеет следующий вид
Случай наличия кратных корней характеристического уравнения.
Если среди корней характеристического уравнения имеются кратные корни, то изложенный выше способ построения фундаментальной системы решений, очевидно, не применим.
Однако и в этом случае удается построить фундаментальную систему решений в элементарных функциях.
Заметим, прежде всего, что если l1есть простое характеристическое число, то независимо от того, будут среди остальных характеристических чисел встречаться кратные или нет, ему всегда соответствует одно частное решение вида:
Таким образом, задача сводится к тому, чтобы найти частные решения, соответствующие кратному корню.
При этом, так же как и для линейного однородного уравнения n-го порядка, оказывается, что одному характеристическому числу кратности k соответствует k линейно независимых частных решений.
Теорема. Если l1 есть характеристическое число кратности k, то ему соответствует решение вида
В частности может случиться, что все эти полиномы вырождаются в постоянные числа. В таком случае k-кратному характеристическому числу l1 будет соответствовать решение вида
Полагая поочередно один из этих произвольных коэффициентов равным единице, а остальные равными нулю, мы построим k линейно независимых решений, соответствующих характеристическому числу l1. Все эти частные решения будут составлены из произведений показательной функции e l 1 x на полиномы от х, степени которых не превышают k−1. Если же полиномы в формулах (39) вырождаются в постоянные числа, то мы получим k линейно независимых частных решений такого же вида, как и в случае простого корня характеристического уравнения.
Если l1 — вещественное характеристическое число, то построенные выше k линейно независимых решений будут вещественными.
Если же система (2) имеет комплексное характеристическое число a + ib кратности k, то оно имеет сопряженное характеристическое число а—ib той же кратности.
Мы выясним эту структуру в следующей главе, где будет дан другой способ построения фундаментальной системы, причем в отличие от настоящего пункта там строится сразу вся фундаментальная система.
будет иметь характеристическое уравнение вида
имеет характеристическое уравнение
Характеристические корни (корни характеристического уравнения) также предоставляют качественную информацию о поведении переменной, эволюция которой описывается динамическим уравнением. Для дифференциального уравнения, параметризованного по времени, эволюция переменной стабильна тогда и только тогда, когда действительная часть каждого корня отрицательна. Для разностных уравнений существует стабильность тогда и только тогда, когда модуль ( абсолютное значение ) каждого корня меньше 1. Для обоих типов уравнений постоянные флуктуации возникают, если имеется хотя бы одна пара комплексных корней.
СОДЕРЖАНИЕ
Вывод
Поскольку e rx никогда не может быть равным нулю, его можно разделить, дав характеристическое уравнение
Формирование общего решения
y ( Икс ) знак равно y D ( Икс ) + y р 1 ( Икс ) + ⋯ + y р час ( Икс ) + y C 1 ( Икс ) + ⋯ + y C k ( Икс ) <\ displaystyle y (x) = y _ <\ mathrm
Пример
Линейное однородное дифференциальное уравнение с постоянными коэффициентами
имеет характеристическое уравнение
По факторинговых характеристическое уравнение в
Отчетливые настоящие корни
y D ( Икс ) знак равно c 1 е р 1 Икс + c 2 е р 2 Икс + ⋯ + c п е р п Икс <\ displaystyle y _ <\ mathrm
Повторяющиеся настоящие корни
d k d Икс k ( ты ) знак равно ты ( k ) знак равно 0 <\ displaystyle <\ frac
Сложные корни
y C ( Икс ) знак равно е а Икс ( C 1 потому что б Икс + C 2 грех б Икс ) <\ displaystyle y _ <\ mathrm
Этот анализ также применяется к частям решений дифференциального уравнения высшего порядка, характеристическое уравнение которого включает невещественные комплексно сопряженные корни.
Замечание.Также в случае, когда правая часть уравнения имеет вид
и, 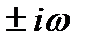
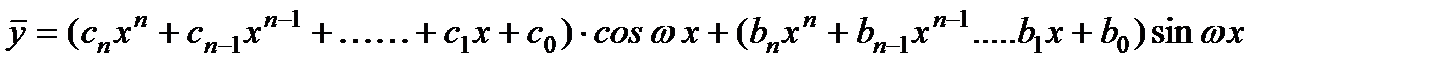
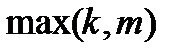
В том случае 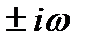
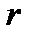
ЗАДАЧИ
1) Для заданных дифференциальных уравнений выписать характеристические уравнения и базисные решения (фундаментальную систему решений), записать общее решение однородного уравнения, 2) для неоднородных уравнений найти частное решение методом неопределенных коэффициентов (комплексных амплитуд), записать решение неоднородного уравнения, 3) при заданных начальных условиях найдите частное решение.
1) 
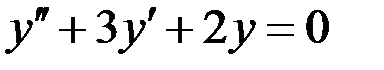
4) 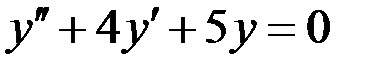
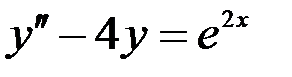
7) 
9) 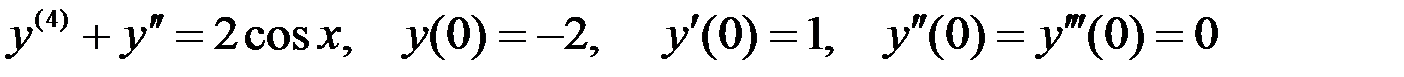
10.) 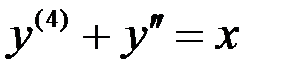
11).
Ответы : 9)
11)
12). Для уравнения затухающихколебаний
Для уравнения вынужденных колебаний
найдите частное решение методом комплексных амплитуд при условии, что 


Контрольные вопросы
1. Что является решением дифференциального уравнения?
Дайте определение общего и частного решений дифференциального уравнения
2. Сформулируйте теорему существования и единственности для дифференциального уравнения первого порядка
3. Определите тип дифференциального уравнения:
4. Решением дифференциального уравнения 
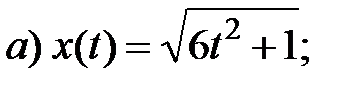
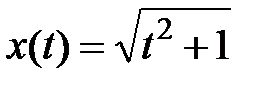
5. Дифференциальное уравнение семейства кривых 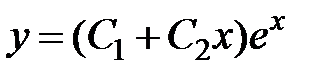
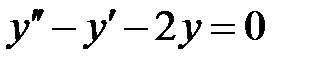
6. Частное решение дифференциального уравнения 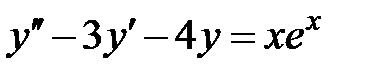
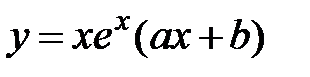
7. Корни характеристического 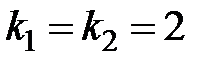
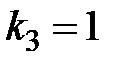
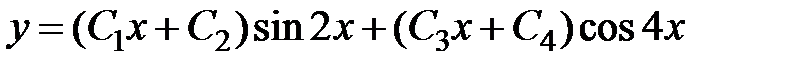
8. Среди перечисленных дифференциальных уравнений уравнениями первого порядка являются:
Варианты ответов:
Должен быть указан не менее двух вариантов ответа
9. Из данных дифференциальных уравнений уравнениями c разделяющимися переменными являются…
Варианты ответов:
Должен быть указан не менее двух вариантов ответа
10. Дано дифференциальное уравнение 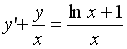
11. Общий интеграл дифференциального уравнения 
12. Общее решение дифференциального уравнения 
13. Решением уравнения первого порядка 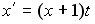
14. Общее решение дифференциального уравнения 
15. Общее решение дифференциального уравнения 
16. Общее решение дифференциального уравнения 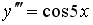
17. Общее решение дифференциального уравнения 
18. Общее решение дифференциального уравнения 
19. Общее решение линейного однородного дифференциального уравнения второго порядка 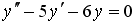
20. Однородному дифференциальному уравнению второго порядка 
21. Дано линейное однородное дифференциальное уравнение 
22. Дано дифференциальное уравнение 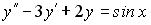
23. Методы приближенного решения дифференциальных уравнений.
Функции комплексной переменной
Срок выполнения 9- 13 недели
Содержание работы
1. Комплексные числа. Алгебраическая, тригонометрическая, показательная форма записи. Действия с комплексными числами
2. Функции комплексной переменной. Аналитические функции
3. Вычет аналитической функции в изолированной особой точке. Вычисление контурных и несобственных интегралов при помощи вычетов.
4. Ряды и преобразования Фурье.
5. Преобразования Лапласа.
6. Решение линейных дифференциальных уравнений и систем уравнений операторным методом.
7. Решение линейных дифференциальных уравнений методом свертки (формулы Дюамеля, Грина).
Литература [2, 3, 4, 11,16, 19]
1. Комплексные числа На множестве действительных чисел не существует такого числа, которое являлось бы корнем простейшего алгебраического уравнения 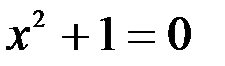 (поскольку квадрат любого действительного числа неотрицателен). Поэтому возникла потребность расширить множество действительных чисел таким образом, чтобы новое множество содержало корни всех алгебраических уравнений. Введение комплексных чисел позволяет достигнуть этой цели. Прежде всего введем новый символ – (поскольку квадрат любого действительного числа неотрицателен). Поэтому возникла потребность расширить множество действительных чисел таким образом, чтобы новое множество содержало корни всех алгебраических уравнений. Введение комплексных чисел позволяет достигнуть этой цели. Прежде всего введем новый символ – 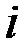 , который называют мнимой единицей таким образом, что , который называют мнимой единицей таким образом, что  . Тогда корни уравнения . Тогда корни уравнения 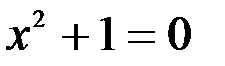 запишутся как запишутся как 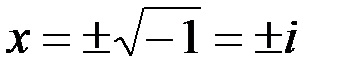 . Алгебраическая форма записи комплексного числа Комплексное число в алгебраической форме записывается как . Алгебраическая форма записи комплексного числа Комплексное число в алгебраической форме записывается как 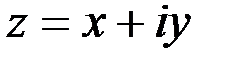 . Здесь . Здесь  – действительное число, называемое реальной или действительной частью комплексного числа. Обозначают: – действительное число, называемое реальной или действительной частью комплексного числа. Обозначают: 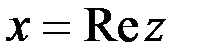 . Действительное число . Действительное число  называют мнимой частью комплексного числа. Обозначают: называют мнимой частью комплексного числа. Обозначают: 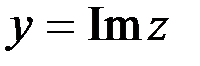 . Таким образом, комплексное число – это упорядоченная пара действительных чисел . Таким образом, комплексное число – это упорядоченная пара действительных чисел 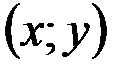 . Если . Если 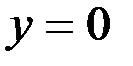 , то комплексное число совпадает с действительным и изображается точкой на действительной оси ОХ. При , то комплексное число совпадает с действительным и изображается точкой на действительной оси ОХ. При  получаются чисто мнимые числа получаются чисто мнимые числа 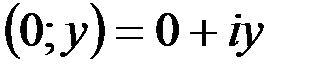 , которые изображаются точкой на мнимой оси OY. Комплексное число , которые изображаются точкой на мнимой оси OY. Комплексное число 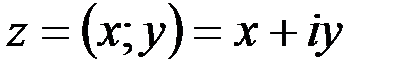 можно отождествить с точкой плоскости OXY или радиусом – вектором можно отождествить с точкой плоскости OXY или радиусом – вектором  . Плоскость OXY будем называть комплексной плоскостью (рис. 1) Два комплексных числа равны, если равны их действительные и мнимые части: . Плоскость OXY будем называть комплексной плоскостью (рис. 1) Два комплексных числа равны, если равны их действительные и мнимые части: 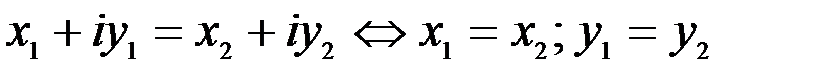 . Два комплексных числа называют сопряженными, если действительные части этих чисел равны, а мнимые отличаются знаком. Обозначают: . Два комплексных числа называют сопряженными, если действительные части этих чисел равны, а мнимые отличаются знаком. Обозначают: 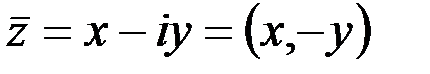 . Над комплексными числами в алгебраической форме определены следующие операции: . Над комплексными числами в алгебраической форме определены следующие операции: Сумма Разность Особо отметим произведение комплексно-сопряженных чисел, которое является числом действительным: Пример 1. Найти значение функции Второе слагаемое есть частное от деления двух комплексных чисел. Используя правило деления комплексных чисел в алгебраической форме, получим: Итак, Пример 2. Решить уравнение По формуле для корней квадратного уравнения имеем: Извлекая корень квадратный из числа |



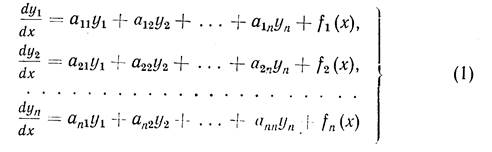
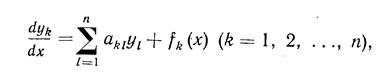
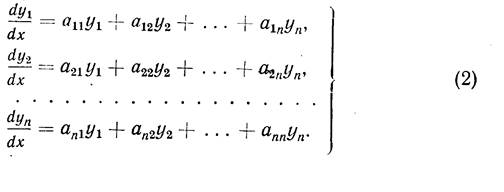
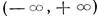
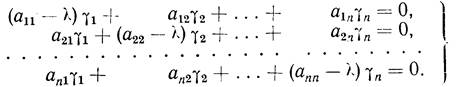
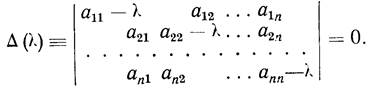

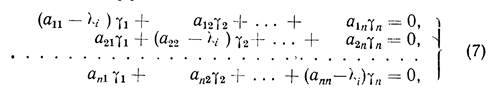
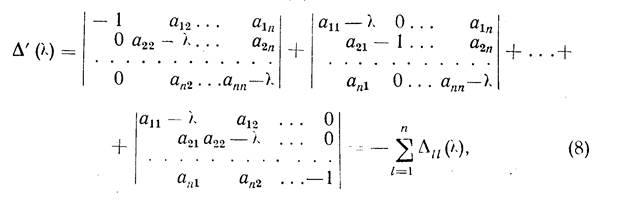

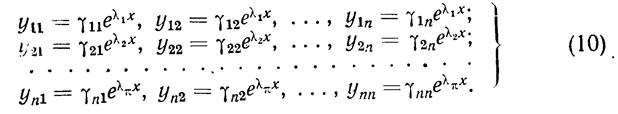

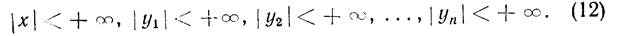
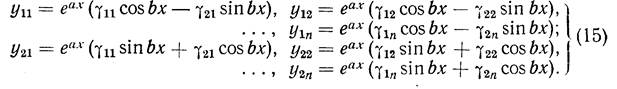
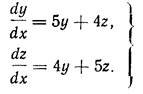
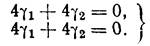
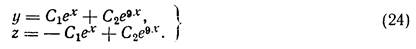
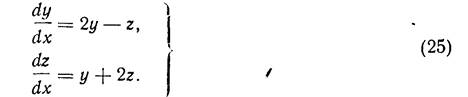
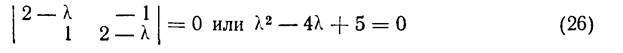

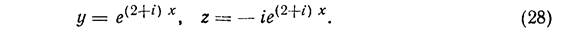
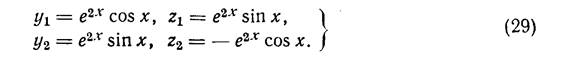
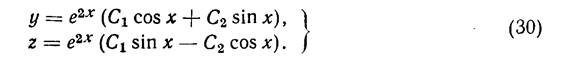
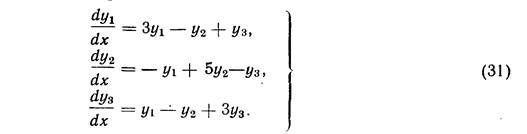
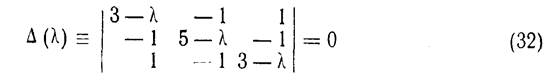
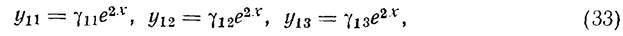
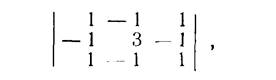
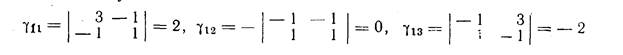
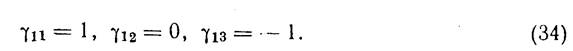
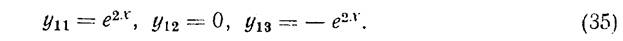
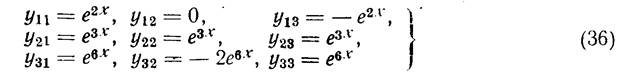
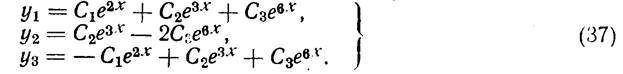

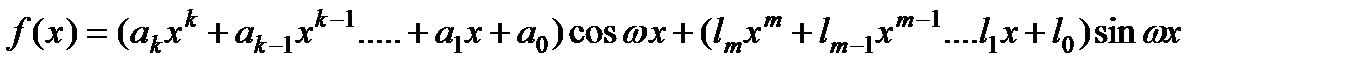
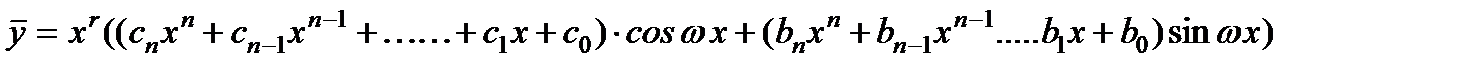
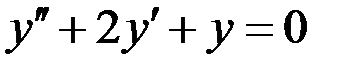
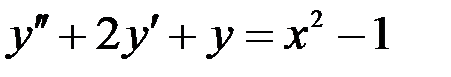
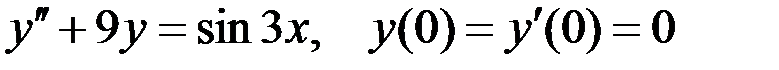


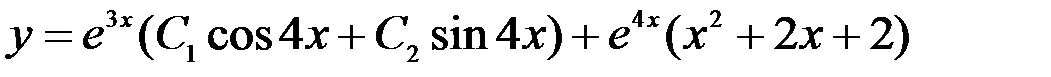

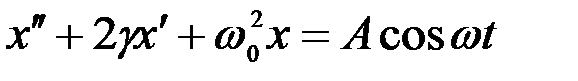
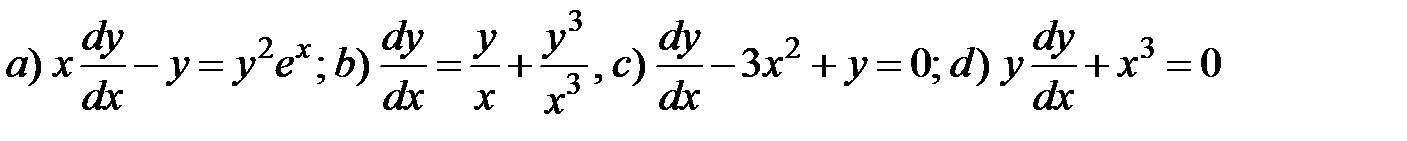
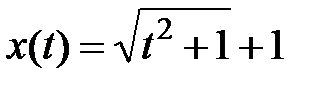
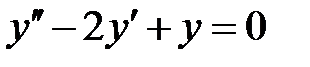
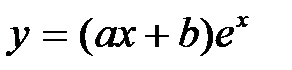

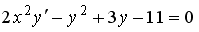

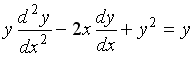
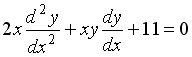
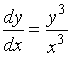
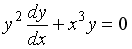
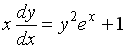
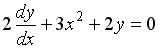
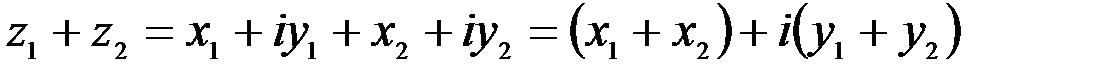 .
.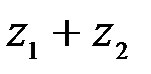 изображается вектором – суммой векторов
изображается вектором – суммой векторов 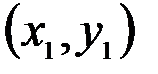 и
и  .
.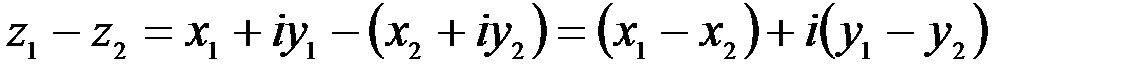 .
.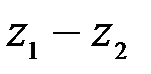 изображается вектором – разностью векторов
изображается вектором – разностью векторов 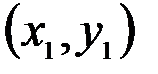 и
и 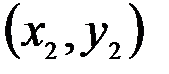 .
.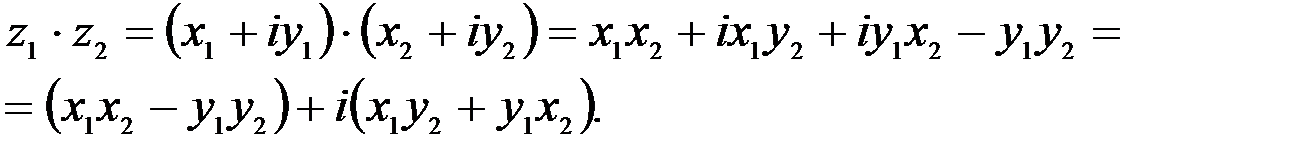
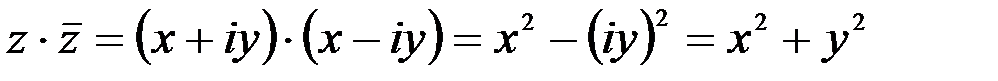 .
.
 при
при 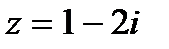 .
.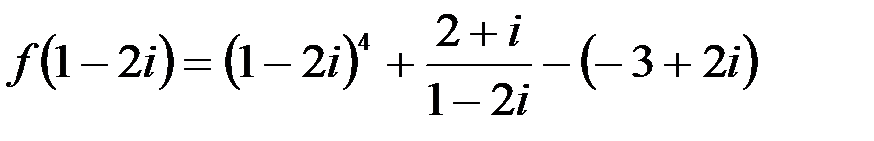 . Для вычисления первого слагаемого воспользуемся формулой бинома Ньютона:
. Для вычисления первого слагаемого воспользуемся формулой бинома Ньютона:
 .
.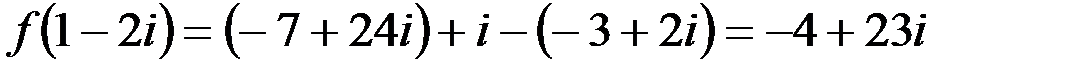 .
.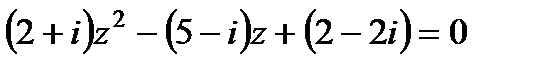 .
. .
. , получим:
, получим: 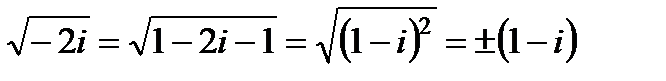 .
. . Отсюда
. Отсюда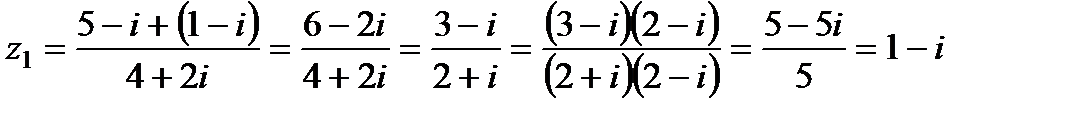
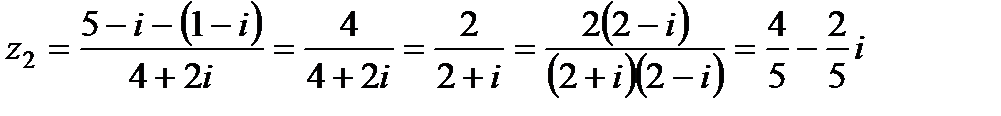 .
.