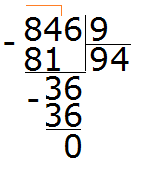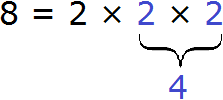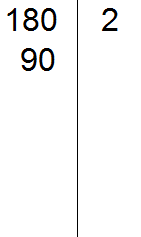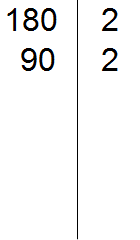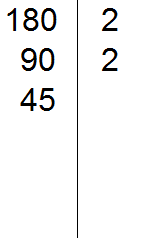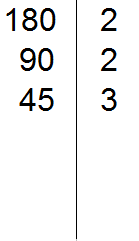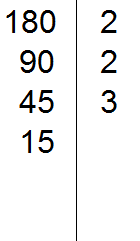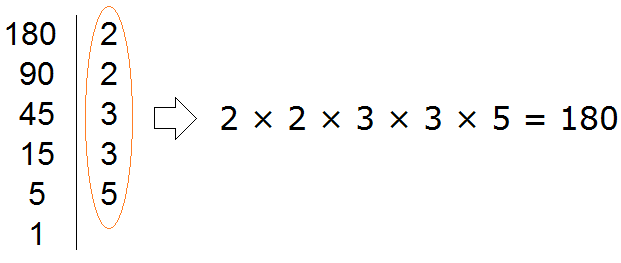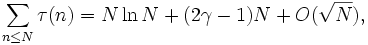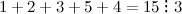что такое кратность чисел в математике
Делители и кратные
В данном уроке мы рассмотрим такие понятия как делители и кратные.
Что такое делитель?
Мы знаем, что делитель это число, показывающее на сколько частей нужно разделить делимое. Например, в выражении 8 : 2 = 4, делителем является число 2. Это число показывает на сколько частей нужно разделить число 8. После разделения получается ответ 4. Как видно из примера, число 8 делится на число 2 без остатка. Говорят, что число 2 является делителем числа 8.
Пример 1. Число 2 является делителем числа 8, поскольку 8 делится на 2 без остатка:
Пример 2. Число 3 является делителем числа 9, поскольку 9 делится на 3 без остатка:
Пример 3. Число 4 не является делителем числа 10 поскольку 10 не делится на 4 без остатка:
10 : 4 = 2 (2 в остатке)
Определение. Делителем числа а называется число, на которое число а делится без остатка.
Делителем числа 12 называется число, на которое 12 делится без остатка.
Попробуем перечислить эти числа:
Все эти числа являются делителями числа 12, поскольку число 12 делится на них без остатка. Покажем это:
12 : 1 = 12
12 : 2 = 6
12 : 3 = 4
12 : 4 = 3
12 : 6 = 2
12 : 12 = 1
Кратные числа
Если какое-нибудь число без остатка разделилось на другое, то его называют кратным этого числа. Например, 6 без остатка делится на 3. Поэтому 6 является кратным числа 3
Определение. Кратным числа а называется число, которое делится без остатка на а.
Кратным числа 5 называется число, которое делится без остатка на 5 .
У любого числа бесконечно много кратных. Например, первыми кратными числа 5, являются числа 5, 10, 15, 20, 25. Все они кратны 5, поскольку делятся на 5 без остатка:
5 : 5 = 1
10 : 5 = 2
15 : 5 = 3
20 : 5 = 4
25 : 5 = 5
Признаки делимости чисел
Признаки делимости чисел используются для того, чтобы ускорить процесс деления чисел. Существует множество признаков делимости и других интересных алгоритмов, значительно ускоряющих решение и освобождающих от излишней волокиты. Рассмотрим наиболее популярные из них.
Признак делимости на 10
Любое число, которое оканчивается нулем, делится без остатка на 10. Чтобы получить частное, достаточно отброс ить цифру 0 в делимом.
Например, 380 : 10 = 38. Мы просто отброс или последний ноль в числе 380.
В случае, если мы имеем выражение такого вида 385 : 10, то получится 38 и 5 в остатке, поскольку 380 : 10 = 38, а пятерка это остаток, который не разделился.
Таким образом, если число оканчивается цифрой 0, то оно делится без остатка на 10. Если же оно оканчивается другой цифрой, то оно не делится без остатка на 10. Остаток в этом случае равен последней цифре числа. Действительно, в примере 385 : 10 = 38 (5 в остатке), остаток равен последней цифре в числе 385, то есть пятерке.
Признак делимости на 5 и на 2
Любое число, которое оканчивается нулем, делится без остатка и на 5, и на 2.
Признак делимости на 5
Если число оканчивается цифрой 0 или 5, то оно делится без остатка на 5.
Признак делимости на 3
Число делится на 3, если сумма цифр этого числа делится на 3. Например, рассмотрим число 27, сумма его цифр 2 + 7 = 9. Девять, как мы знаем делится на 3, значит и 27 делится на 3:
Признак делимости на 9
Число делится на 9, если сумма его цифр делится на 9. Например, рассмотрим число 18. Сумма его цифр 1 + 8 = 9. Девять делится на девять, значит и 18 делится на 9
Рассмотрим число 846. Сумма его цифр 8 + 4 + 6 = 18. Восемнадцать делится на девять, значит и 846 делится на 9:
Чётные и нечётные числа
Чётным называется число, которое делится без остатка на 2. Например, число 20 является четным, поскольку оно делится без остатка на 2:
Нечётным называется число, если при его делении на 2, остаётся остаток 1. Например число 21 является нечетным, поскольку после его деления на 2 остается остаток 1:
21 : 2 = 10 (1 в остатке)
Как распознать чётное число от нечетного, не выполняя деления на 2? Очень просто. Из однозначных чисел чётными являются числа 0, 2, 4, 6, 8, а нечетными являются 1, 3, 5, 7, 9. Если число оканчивается чётной цифрой, то это число является чётным. Если число оканчивается нечетной цифрой, то это число является нечетным.
Например, число 308 чётно, поскольку оно оканчивается чётной цифрой. Число 1024 тоже четно, поскольку оканчивается четной цифрой.
А числа 305 и 1027 являются нечётными, поскольку они оканчиваются нечётными цифрами.
Простые и составные числа
Простым называется число, которое делится без остатка на единицу и на само себя. Другими словами, имеет только два делителя. Например, число 5 делится без остатка на единицу и на само себя:
Значит, число 5 является простым числом.
Составным же называется число, которое имеет два и более делителя. Например, число 4 составное, поскольку у него два и более делителя: 4, 2 и 1
Значит, число 4 является составным числом.
Разложение составного числа на простые множители
Любое составное число можно разложить на простые множители. Чем-то похожим мы занимались в уроке замены в выражениях. Из этого урока мы узнали, что любое число, входящее в выражение, можно заменить на то же самое, но записанное в другом виде.
Суть разложения числа на простые множители заключается в том, чтобы представить это число в виде произведения нескольких простых множителей.
Разложим число 4 на простые множители. Для этого соберем данное число из других чисел, при этом соединим их знаком умножения (×). Число 4 состоит из чисел 2 и 2. Эти два числа и являются простыми множителями, из которых состоит число 4
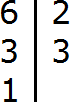
Разложим на множители число 6. Число 6 можно собрать из чисел 2 и 3. Эти два числа и являются простыми множителями, из которых состоит число 6
Большие числа раскладываются таким же образом. Сначала их раскладывают на большие множители, затем эти большие множители раскладывают на маленькие. И так до тех пор, пока каждый множитель не станет простым числом.
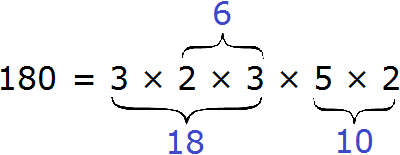
Например, разложим число 180 на простые множители. Число 180 это два множителя 18 и 10
Теперь раскладываем множители 18 и 10 на другие множители:
Теперь раскладываем выделенную синюю шестерку. Это последний большой множитель, который можно разложить на простые множители:
Теперь собираем все простые множители вместе:
На множители можно разложить только составное число. Простое число на множители не раскладывается. Именно поэтому, когда разложение доходит до простых чисел, мы эти простые числа дальше не раскладываем.
Есть и второй способ разложения на простые множители. Он проще и хорошо подходит для больших чисел. Суть этого способа заключается в том, что сначала проводится вертикальная линия. Затем слева от этой линии записываются делимые, а справа — делители, которые впоследствии собирают во множители.
При разложении числа этим способом, используют признаки делимости, такие как: признаки делимости на 2, на 3, на 5 и другие.
Например, разложим предыдущее число 180 этим способом.
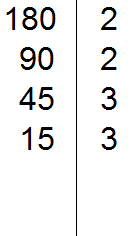
Проводим вертикальную линию и слева записываем первое делимое 180
Теперь применяем признаки делимости. В первую очередь проверяем делится ли 180 на 2. Если делится, то нужно записать эту двойку справа от вертикальной линии.
180 делится на 2, поскольку 180 оканчивается нулём. Записываем двойку справа от вертикальной линии:
Теперь делим 180 на 2 и получаем второе делимое 90. Записываем это делимое слева от вертикальной линии:
Теперь делим 90. Снова применяем признаки делимости. Проверяем делится ли 90 на 2.
90 делится на 2, поскольку 90 оканчивается нулём. Записываем двойку справа от вертикальной линии:
Теперь делим 90 на 2, получаем третье делимое 45. Записываем это делимое слева от вертикальной линии:
Теперь делим 45. Снова применяем признаки делимости. Проверяем делится ли 45 на 2.
45 на 2 не делится. Тогда проверяем делится ли 45 на 3.
45 делится на 3, поскольку сумма цифр 4 и 5 делится на 3. Записываем тройку справа от вертикальной линии:
Делим 45 на 3, получаем четвёртое делимое 15. Записываем это делимое слева от вертикальной линии:
Теперь делим 15. Проверяем делится ли 15 на 2.
15 не делится на 2. Тогда проверяем делится ли 15 на 3.
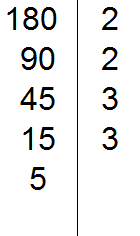
15 на 3 делится, поскольку сумма цифр 1 и 5 делится на 3. Записываем тройку справа от вертикальной линии:
Делим 15 на 3, получаем пятое делимое 5. Записываем пятёрку слева от вертикальной линии:
Теперь делим 5. Проверяем делится ли 5 на 2.
5 не делится на 2. Тогда проверяем делится ли 5 на 3.
5 не делится на 3. Тогда проверяем делится ли 5 на 5.
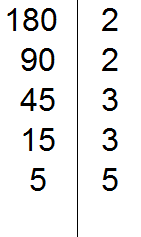
5 делится на 5. Записываем эту пятёрку справа от вертикальной линии:
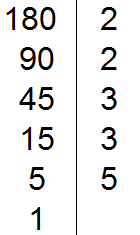
Делим 5 на 5, получаем шестое делимое 1. Записываем эту единицу слева от вертикальной линии:
На этом деление завершается, поскольку мы достигли единицы. Делители, которые записывают справа от вертикальной линии должны быть простыми числами. Поэтому, когда делимое 5 не разделилось на 2, а затем не разделилось на 3, мы попробовали разделить его на 5, не пробуя разделить на 4, поскольку 4 является не простым, а составным числом.
Теперь переписываем в один ряд все делители, которые записаны справа от вертикальной линии. Они и будут разложением числа 180 на простые множители. Желательно записывать их, начиная с самых малых. Это позволяет упорядочить их по возрастанию:
Не расстраивайтесь, если будете испытывать затруднения при разложении чисел на простые множители. Эта тема требует немного практики. Для тренировки можете разложить на простые множители следующие числа: 256, 378, 512.
Нахождение делителей числа
В начале данного урока было сказано, что делителем называется число, на которое другое число делится без остатка.
Например, число 2 является делителем числа 6, поскольку число 6 можно без остатка разделить на 2
6 : 2 = 3
Ещё делителем числа 6 является число 3
6 : 3 = 2
Ещё делителем числа 6 является число 1
6 : 1 = 6
Наконец, делителем числа 6 является само это число
6 : 6 = 1
Перечислим все делители числа 6
1, 2, 3, 6
Иногда возникает необходимость найти все делители какого-нибудь числа. Чтобы понять, как это делается, рассмотрим несколько примеров.
Пример 1. Найти делители числа 12
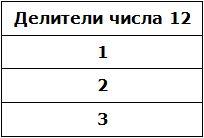
Во-первых, единица является делителем любого числа. Пусть и у нас первым делителем числа 12 будет 1
Теперь раскладываем число 12 на простые множители:
Получили разложение 2 × 2 × 3.
В процессе разложения числа 12 на простые множители, мы делили его на числа 2 и 3. На них число 12 разделилось без остатка, значит они тоже являются делителями числа 12. Внесём эти два числа в нашу таблицу делителей:
Чтобы получить остальные делители числа 12, нужно найти все возможные произведения его простых множителей между собой. Получаемые в результате ответы и будут остальными делителями числа 12.
Число 12 мы разложили на простые множители 2 × 2 × 3. Найдём все возможные произведения этих простых множителей между собой. Первое произведение это 2 × 2. Это произведение равно 4
Занесём число 4 в нашу таблицу делителей
Следующее возможное произведение из простых множителей числа 12 это произведение 2 × 3. Данное произведение равно 6. Занесём число 6 в нашу таблицу делителей:
Последнее возможное произведение из простых множителей числа 12 это произведение из всех его множителей, а именно 2 × 2 × 3. Это произведение равно 12. Занесём число 12 в нашу таблицу делителей:
Таким образом, делителями числа 12 являются числа 1, 2, 3, 4, 6, 12.
На основании приведённого примера можно сформировать правило для нахождения делителей числа:
Чтобы найти делители числа, нужно:
Пример 2. Найти делители числа 6
Первым делителем числа 6 запишем единицу:
Теперь разложим число 6 на простые множители:
Выпишем из полученного разложения те множители, которые являются делителями числа 6. Видим, что это множители 2 и 3. Они будут следующими делителями числа 6. Допишем их к нашим делителям:
1, 2, 3
1, 2, 3, 6
Кратное
Делимость — одно из основных понятий арифметики и теории чисел, связаное с операцией деления.
Содержание
Определение
Обозначения
Связанные определения
Свойства
Число делителей
Обобщения
Понятие делимости обобщается на произвольные кольца, например кольцо многочленов.
См. также
Полезное
Смотреть что такое «Кратное» в других словарях:
КРАТНОЕ — число, делящееся на данное целое число без остатка, напр. 12 кратно 3. Общее кратное нескольких целых чисел число, делящееся на каждое из них в отдельности, напр. 180 общее кратное чисел 30, 18, 2. При арифметических действиях особое значение… … Большой Энциклопедический словарь
кратное — ого; ср. Целое число, делящееся на данное без остатка. Шесть к. чисел два и три. Наименьшее общее к. нескольких чисел. * * * кратное число, делящееся на данное целое число без остатка, например 12 кратно 3. Общее кратное нескольких целых чисел … … Энциклопедический словарь
Кратное — натурального (целого положительного) числа а, натуральное число, делящееся на а без остатка. Так, 156 есть К. 13, тогда как 108 не является К. 13. Число n, которое делится на каждое из чисел а, b. m, называется общим К. этих чисел. Из … Большая советская энциклопедия
Кратное — ср. Целое число, делящееся на какое либо число без остатка. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
КРАТНОЕ — число, делящееся на данное целое число без остатка, напр. 12 кратно 3. Общее К. неск. целых чисел число, делящееся на каждое из них в отдельности, напр. 180 общее К. чисел 30, 18, 2. При арифметич. действиях особое значение имеет наименьшее общее … Естествознание. Энциклопедический словарь
кратное — кр атное, ого … Русский орфографический словарь
кратное — ого; ср. Целое число, делящееся на данное без остатка. Шесть кра/тное чисел два и три. Наименьшее общее кра/тное нескольких чисел … Словарь многих выражений
кратное (число) — кратный многократный множественный составной параллельный — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы… … Справочник технического переводчика
Что такое кратное число
Определение кратного числа
Некоторые признаки делимости натуральных чисел
Признак делимости на 2.
Число делится на 2, если его последняя цифра есть число четное (то есть 2, 4, 6, 8) или 0.
Признак делимости на 3.
Число делится на 3, если сумма его цифр делится на 3.
Признак делимости на 4.
Признак делимости на 5.
Число делится на 5, если оно заканчивается либо на 0, либо на 5.
Признак делимости на 8.
Признак делимости на 9.
Число делится на 9, если сумма его цифр делится на 9.
Признак делимости на 11.
Число делится на 11, если сумма цифр, стоящих на четных местах либо равна сумме цифр, стоящих на нечетных местах, либо отличается от неё на число, делящееся на 11.
Признак делимости на 25.
Задание. Среди ниже перечисленных чисел выбрать числа кратные 3:
$$27: 36 ; 58 ; 1119 ; 2345 ; 12354$$
Решение. Будем использовать признак делимости на 3, для этого найдем сумму цифр для каждого числа:
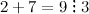


Таким образом, на 3 делятся числа:
$$27 ; 36 ; 1119: 12354$$
Наименьшее общее кратное (НОК)
Общим кратным нескольких натуральных чисел называется натуральное число, являющееся кратным для каждого из них. Наименьшее из всех кратных называется наименьшим общим кратным (НОК).
Алгоритм нахождения наименьшего общего кратного нескольких чисел:
Что такое кратное число не по зубам? Тебе ответит эксперт через 10 минут!
Задание. Найти НОК(360; 420)
Решение. Запишем каноническое разложение заданных чисел:
Наименьшее общее кратное (НОК): определение, примеры и свойства
Приступим к изучению наименьшего общего кратного двух и более чисел. В разделе мы дадим определение термина, рассмотрим теорему, которая устанавливает связь между наименьшим общим кратным и наибольшим общим делителем, приведем примеры решения задач.
Общие кратные – определение, примеры
В данной теме нас будет интересовать только общие кратные целых чисел, отличных от нуля.
Общее кратное целых чисел – это такое целое число, которое кратно всем данным числам. Фактически, это любое целое число, которое можно разделить на любое из данных чисел.
Определение общих кратных чисел относится к двум, трем и большему количеству целых чисел.
0 является общим кратным для любого множества целых чисел, отличных от нуля.
Для всех ли чисел можно найти НОК?
Общее кратное можно найти для любых целых чисел.
Сколько всего общих кратных могут иметь данные целые числа?
Группа целых чисел может иметь большое количество общих кратных. Фактически, их число бесконечно.
Наименьшее общее кратное (НОК) – определение, обозначение и примеры
Вспомним понятие наименьшего числа из данного множества чисел, которое мы рассматривали в разделе «Сравнение целых чисел». С учетом этого понятия сформулируем определение наименьшего общего кратного, которое имеет среди всех общих кратных наибольшее практическое значение.
Наименьшее общее кратное данных целых чисел – это наименьшее положительное общее кратное этих чисел.
Не для всех групп данных чисел наименьшее общее кратное очевидно. Часто его приходится вычислять.
Связь между НОК и НОД
Наименьшее общее кратное и наибольший общий делитель связаны между собой. Взаимосвязь между понятиями устанавливает теорема.
Установление связи между НОК и НОД позволяет находить наименьшее общее кратное через наибольший общий делитель двух и более данных чисел.
Теорема имеет два важных следствия:
Наименьшее общее кратное трех и большего количества чисел
Для того, чтобы найти наименьшее общее кратное нескольких чисел, необходимо последовательно найти НОК двух чисел.
Доказать верность второй теоремы нам поможет первое следствие из первой теоремы, рассмотренной в данной теме. Рассуждения строятся по следующему алгоритму:
Кратное число

Всего получено оценок: 158.
Всего получено оценок: 158.
Математика имеет много специфических понятий, среди которых кратное число и делимость чисел. Сегодня мы разберем понятие кратности, а так же все понятия из математики 6 класса, которые связаны с кратностью.
Деление
Операция деления является обратной для операции умножения. Деление показывает, сколько раз одно число умножили на другое, чтобы получить изначальный результат. Для нахождения результата простейших операций деления пользуются таблицей умножения.
Для более сложных примеров пользуются деление в столбик. Так же различают деление с остатком, нацело и деление с дробным остатком:
Так же вместо деления всегда можно записать обычную или неправильную дробь, но в качестве ответа такая запись не подойдет.
Отрицательные числа так же можно поделить нацело. Так же, как и в делении отрицательных чисел на положительные и положительные на отрицательные. Нельзя так же забывать, что на деление действует правило знаков. То есть деление отрицательного числа на положительное дает отрицательный результат. Деление отрицательного числа на отрицательное – положительный результат.
Кратность и делимость
Разберем эти понятия на числе 9. Так для числа 9 кратными будут 18, 27, 36 и так далее. То есть кратными называют числа, которые можно поделить на заданное число нацело.
Делимостью же называют способность самого числа поделиться нацело. То есть для 9 делителями будут числа 9,3,1. Число делителей – ограниченно, число кратных – нет.
Бывают числа кратные для нескольких значений одновременно.
Для нескольких чисел существует два понятия, связанных с делимостью и кратностью:
Иногда ученики пытаются найти таблицу кратных чисел. Но такого материала просто не существует. Нельзя свести в одну таблицу все числа. А для наиболее простых от 1 до 10 существует таблица умножения.
Что мы узнали?
Мы вспомнили, что такое операция деления. Рассказали, что такое кратность и делимость чисел. Разделили два этих понятия. Сказали о том, что таблицы кратности в математике пока не изобрели. Рассказали, в каких математических показателях используются понятия кратности и делимости.