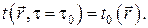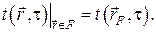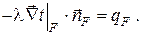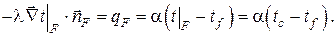что такое краевые условия теплообмена
Краевые условия для уравнения теплопроводности
Дифференциальное уравнение теплопроводности в однородных изотропных средах в терминах математической физики есть неоднородное дифференциальное уравнение в частных производных параболического типа (первого порядка по времени и второго порядка по пространственным координатам). Если внутренние тепловыделения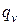 
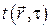
зависят от температуры
, то уравнение теплопроводности будет нелинейным, если плотность внутренних источников теплоты зависит от температуры нелинейным образом. Если же плотность внутренних источников теплоты пропорциональна первой степени температуры или не зависит от температуры, то уравнение теплопроводности будет либо линейным, либо квазилинейным, оставаясь, тем не менее, уравнением параболического типа.
Как бы то ни было, любое дифференциальное уравнение может дать однозначное решение только если заданы условия однозначности. В случае дифференциального уравнения параболического типа должно быть задано начальное условие
Что касается граничных условий, то-есть условий теплообмена на границе рассматриваемого объёма с окружающей (контактирующей с ним) средой, то здесь имеют место несколько (а именно, четыре) возможностей, каждая из которых характеризует тот или иной тип теплового взаимодействия с внешней средой. Эти возможности обычно нумеруются римскими цифрами. Перечислим их.
I. Граничные условия I рода
В этом случае задаётся распределение температур на физической границе рассматриваемого объёма, т.е. задаётся функция координат поверхности и времени
II. Граничные условия II рода
Задаётся плотность теплового потока на границе рассматриваемого тела, что позволяет записать
Такие граничные условия обычно имеют место при решении задач теплопроводности в твёрдых телах с теплообменом излучением на границах. Чаще всего такие задачи возникают при решении задач в металлургической теплотехнике, в астрофизике и т.д.
III. Граничные условия III рода
Граничные условия III рода наиболее распространены при решении задач теплопроводности в энергетике, в металлургии и в химической технологии.
Граничные условия III рода описывают в математической форме условия теплообмена внешней поверхности твёрдого тела с контактирующей с ним жидкостью или газом, т.е. со средами, допускающими конвективные движения с перемешиванием.
Математическая формулировка граничных условий III рода базируется на гипотезе (законе) Ньютона-Рихмана, согласно которой тепловой поток с поверхности к омывающей её жидкости пропорционален разности температур, т.е.
Здесь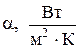 
есть по определению коэффициент теплоотдачи, представляющий собой количество теплоты, снимаемое в единицу времени с единичной поверхности при единичной разности температур.
Экспериментальное обоснование гипотезы Ньютона-Рихмана состоит в том, что, как показывают экспериментальные исследования, количество теплоты, снимаемое с поверхности твёрдого тела, прямо пропорционально поверхности и разности температур поверхности и жидкости вдали от неё (как говорят, в ядре потока). Нахождение величины коэффициента теплоотдачи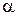 
является задачей экспериментальной теплофизики (вплоть до теоретических исследований) и будет обсуждено в дальнейшем изложении курса. В задачах теплопроводности значения коэффициентов теплоотдачи будут считаться заданными и постоянными.
IV. Граничные условия IV рода
Граничные условия IV рода задают условия теплообмена на границе контакта твёрдых поверхностей. В частности, если контакт твёрдых поверхностей неидеален, то на границе их контакта в математическом смысле будет иметь место скачок температуры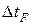 
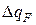
, а при наличии тепловыделения на поверхностях контакта будет иметь место дополнительный поток тепла 
. В этом случае граничные условия математически запишутся в виде
1. 2. Основные понятия и определения
Теплообмен между стенкой и соприкасающейся с ней жидкостью (газом) носит название теплоотдачи.
Тело, имеющее более высокую температуру Т1, называется теплоотдающим телом. Второе тело, имеющее более низкую температуру Т2, называется тепловоспринимающим телом.
Количество тепла, проходящее через данную поверхность в единицу времени, называется тепловым потоком и обозначается Q (Вт). Тепловой поток, проходящий через единицу поверхности, называется удельным тепловым потоком и обозначается q (Вт/м 2 ).
Теплообмен между жидкостями (газами или газом и жидкостью), разделенными твердой стенкой, называется теплопередачей через стенку. 
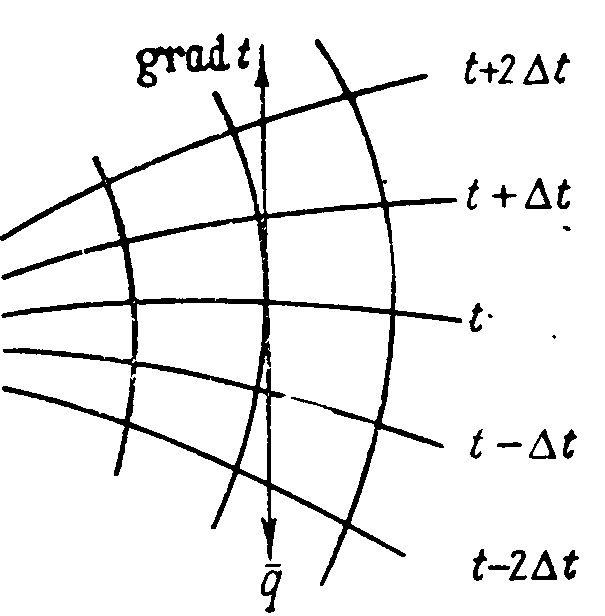
Температурным градиентом называется предел отношения – изменения температуры к расстоянию по нормали к изотермической поверхности при стремлении последнего к нулю.
(2.7)
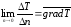
Температурный градиент есть вектор, направленный по нормали к изотермической поверхности в точке А. За положительное направление градиента принимают направление возрастания температур. Для разных точек, лежащих на одной и той же поверхности уровня, величина градиента неодинакова: она будет больше там, где меньше расстояние n между поверхностями уровня.
1. 3. Основной закон теплопроводности
Количественная оценка тепла, проходящего внутри данного тела вследствие теплопроводности, базируется на гипотезе, высказанной в 1822 году французским ученым Фурье. По этой гипотезе элементарное количество тепла dQ, проходящее через элемент изотермической поверхности dF за промежуток времени d, пропорциональнотемпературному градиенту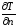 
:
.
Если отнести количество тепла, переданное посредством теплопроводности, к единице изотермической поверхности и к единице времени, то получим удельный тепловой поток
.
,
называемый тепловым потоком, нормален к поверхности уровня и направлен в сторону убывания температуры.
1. 4. Дифференциальное уравнение теплопроводности
При решении всех без исключения задач теплопроводности как при стационарном, так и при нестационарном тепловом режимах, обязательным является знание поля температур.
При выводе дифференциального уравнения теплопроводности будем считать, что физические параметры: (коэффициент теплопроводности), с (теплоемкость) и (удельный вес) не зависят от координат и времени в пределах всего поля.
.
Уравнение называется основным дифференциальным уравнением теплопроводности.
Оно устанавливает связь междувременным и пространственным изменением температуры в любой точке поля.
.
называется коэффициентом температуропроводности тела.
1. 5. Краевые условия. Расчетное уравнение теплоотдачи
Основное дифференциальное уравнение теплопроводности характеризует пространственно-временное изменение температуры в любой точке поля, объединяя все без исключения явления теплопроводности независимо от геометрической формы тела, его физических свойств и условий взаимодействия с окружающей средой.
Краевые граничные условия связаны с взаимодействием изучаемого тела с окружающей средой (например, распределение температур на поверхности тела для каждого момента времени). Граничные краевые условия в свою очередь могут быть заданы тремя способами:
Граничное условие первого рода задается распределением температур по поверхности тела для любого момента времени.
Граничное условие второго рода задается тепловым потоком в каждой точке поверхности тела для каждого момента времени.
Граничное условие третьего рода заключается в задании температуры среды, окружающей изучаемое тело, и закона теплоотдачи между поверхностями и окружающей средой.
Что такое краевые условия теплообмена
Временные краевые условия к уравнению распространения тепла сводятся к заданию скалярной функции
(5.3.1)
дающей распределение температуры в рассматриваемой области в некоторый момент времени. Пространственные краевые условия сводятся к заданию условий теплообмена на ограждающих поверхностях. Способов задания таких условий три.
Пространственное краевое условие первого рода задается распределением температуры на ограждающих поверхностях как функции положения точки поверхности и времени. Эта функция должна быть задана для всех точек ограждающих поверхностей. В ряде практически важных задач оказывается возможным положить, что температура на твердой стенке одинакова во всех ее точках.
Пространственное краевое условие второго рода задается тепловым потоком, пронизывающим ограждающую поверхность, как функцией точки этой поверхности и времени.
Пространственное краевое условие третьего рода связывает температуру твердой стенки с температурой окружающей среды через заданное значение коэффициента теплоотдачи от стенки к этой среде. В этом случае температура в данной точке ограждающей поверхности
(5.3.2)
где 
— характерная температура среды. Выражая плотность теплового потока q через градиент температуры в твердой стенке, получаем
(5.3.3)
(5.3.4)
Величина 
имеет размерность 
и называется относительным коэффициентом теплоотдачи. Величина, обратная относительному коэффициенту теплоотдачи, т. е.
(5.3.5)
имеет размерность длины и называется дополнительной стенкой. Физический смысл этого термина заключается в том, что значение дополнительной стенки равно толщине плоского слоя, имеющего ту же теплопроводность, что и рассматриваемое твердое тело, в котором при данном тепловом потоке q имеет место перепад температур:
(5.3.6)