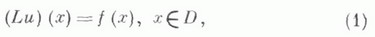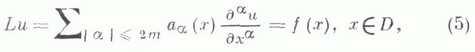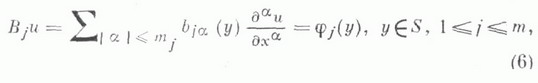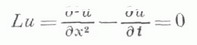что такое краевая задача
Краевая задача
Краевая задача — дифференциальное уравнение (система дифференциальных уравнений) с заданными линейными соотношениями между значениями искомых функций на начале и конце интервала интегрирования.
Решение краевой задачи ищется в виде линейной комбинации решений однородных задач Коши, соответствующих заданному уравнению при линейно независимых векторах начальных условий, и решения неоднородной задачи Коши с произвольными начальными условиями.
Пример краевой задачи:
(система неоднородных обыкновенных дифференциальных уравнений с переменными коэффициентами, заданная на участке 
)
Граничные условия (общий вид для всех краевых задач): 
Где 
— матрицы, 
— вектор неизвестных, 
— 
-вектор (делающий систему неоднородной), 
— -вектор
Общий вид решения:
Удовлетворение граничных условий достигается за счёт подбора коэффициентов 
. Эти коэффициенты находятся путём решения системы линейных уравнений.
Содержание
Численные методы решения краевой задачи
См. также
Ссылки
Литература
Владимиров В.С., Жаринов В.В. Уравнения математической физики. — Физматлит, 2004. — ISBN 5-9221-0310-X
Полезное
Смотреть что такое «Краевая задача» в других словарях:
КРАЕВАЯ ЗАДАЧА — задача выделения ф ции, удовлетворяющей заданному условию на границе нек рой области, из класса ф ций, определённых в этой области. Обычно класс ф ций является набором решений (общим решением) данного дифференц. ур ния. Если речь идёт о системе… … Физическая энциклопедия
КРАЕВАЯ ЗАДАЧА — часто встречающаяся в математической физике задача, в которой из класса функций, определенных в данной области, требуется найти функцию, удовлетворяющую на границе (крае) этой области заданным условиям … Большой Энциклопедический словарь
краевая задача — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN boundary value problem … Справочник технического переводчика
КРАЕВАЯ ЗАДАЧА — теории потенциала основная задача потенциала теории как классической, так и абстрактной. Поскольку классические ньютонов и логарифмич. потенциалы удовлетворяют определенным дифференциальным уравнениям с частными производными эллиптич. типа, а… … Математическая энциклопедия
КРАЕВАЯ ЗАДАЧА — для уравнения с частными производными задача определения в нек рой области Dпеременных решения u(x) уравнения удовлетворяющего на границе Sэтой области (или ее части) определенным краевым условиям Как правило, краевые условия связывают граничные… … Математическая энциклопедия
краевая задача — часто встречающаяся в математической физике задача, в которой из класса функций, определённых в данной области, требуется найти функцию, удовлетворяющую на границе (крае) этой области заданным условиям. * * * КРАЕВАЯ ЗАДАЧА КРАЕВАЯ ЗАДАЧА, часто… … Энциклопедический словарь
краевая задача — kraštinis uždavinys statusas T sritis Energetika apibrėžtis Uždavinys, kai iš galimo begalinio funkcijų skaičiaus reikia rasti funkciją, kuri sutinka su nurodytomis ribinėmis sąlygomis. atitikmenys: angl. boundary problem vok. Randwertaufgabe, f; … Aiškinamasis šiluminės ir branduolinės technikos terminų žodynas
краевая задача — kraštinis uždavinys statusas T sritis automatika atitikmenys: angl. boundary value problem vok. Randwertproblem, n rus. краевая задача, f pranc. problème aux limites, m … Automatikos terminų žodynas
краевая задача — kraštinis uždavinys statusas T sritis fizika atitikmenys: angl. boundary problem; boundary value problem vok. Randwertaufgabe, f; Randwertproblem, n rus. граничное задание, n; краевая задача, f pranc. problème aux limites, m … Fizikos terminų žodynas
КРАЕВАЯ ЗАДАЧА — для эллиптического уравнения задача отыскания регулярного в области Dрешения иэллиптического уравнения удовлетворяющего нек рым дополнительным условиям на границе Г области D. Классические К. з. являются частными случаями следующей задачи: найти… … Математическая энциклопедия
Краевые задачи для уравнений высших порядков
Рассмотрим для простоты уравнение второго порядка
Уравнения (1) и (2) могут быть преобразованы одно в другое. Уравнение вида (2) называются самосопряженными.
Весьма общий вид краевых условий для уравнения второго порядка следующий:
где — заданные постоянные, причем не равны одновременно нулю.
y'(0)=y'(\pi). \end
Вообще говоря, краевые задачи не всегда разрешимы, т.е. не всегда существует такое решение, которое принимает требуемые значения на концах интервала. Например, краевая задача
не имеет ни одного решения. Задача
Наряду с простыми собственными значениями, когда одному собственному значению отвечает одна собственная функция (с точностью до постоянного множителя), существуют кратные собственные значения, когда собственному значению отвечают две или более линейно независимые собственные функции.
При решении краевых задач (для линейных однородных дифференциальных уравнений) поступают так: находят общее решение данного дифференциального уравнения
Решение. Общее решение данного уравнения
Полагая в (6) и в (5) и учитывая краевые условия, получаем для нахождения значений постоянных и неоднородную линейную систему
Определитель этой системы
следовательно, она имеет единственное решение
Подставляя найденные значения и в (5), получаем решение заданной краевой задачи
Пример 2. Найти собственные значения и собственные функции краевой задачи
Решение. Обшее решение уравнения (7)
Полагая (9) и в (10) и учитывая краевые условия (8), получаем для нахождения и однородную линейную систему
Система (11) будет иметь ненулевые решения тогда и только тогда, когда ее определитель равен нулю; приравняв его нулю, получаем уравнение для нахождения собственных значений данной краевой задачи:
являющиеся решениями краевой задачи (7)–(8).
При решении задач математической физики, приводящих к задачам на определение собственных значений, часто получаются дифференциальные уравнения вида
Решение. Данное уравнение является уравнением Эйлера. Его общее решение имеет вид
Краевая задача
Определение температуры во всех точках железного стержня с одним концом, поддерживаемым на уровне абсолютного нуля, а на другом конце при температуре замерзания воды, было бы краевой задачей.
Если проблема зависит как от пространства, так и от времени, можно указать значение проблемы в данной точке для всего времени или в данное время для всего пространства.
Конкретно, примером граничного значения (в одном пространственном измерении) является задача
Без граничных условий общее решение этого уравнения есть
Граничные условия
Граничное условие, которое определяет значение самой функции, является граничным условием Дирихле или граничным условием первого типа. Например, если один конец железного стержня удерживается на абсолютном нуле, тогда значение проблемы будет известно в этой точке пространства.
Граничное условие, которое определяет значение нормальной производной функции, является граничным условием Неймана или граничным условием второго типа. Например, если на одном конце железного стержня установлен нагреватель, то энергия будет добавляться с постоянной скоростью, но фактическая температура не будет известна.
Примеры
Дифференциальные операторы
Электромагнитный потенциал
КРАЕВАЯ ЗАДАЧА
удовлетворяющего на границе Sэтой области (или ее части) определенным краевым условиям
Как правило, краевые условия связывают граничные значения решения с его производными до нек-рого порядка, т. е. Вявляется дифференциальным оператором. Однако встречаются и краевые условия других типов.
Для данного дифференциального уравнения целесообразность рассмотрения той или иной К. з. часто определяется понятием ее корректной постановки. Именно, К. з. корректно поставлена, если ее решение существует, единственно и непрерывно зависит от данных этой задачи. Различные типы дифференциальных уравнений требуют различных корректно поставленных К. з., и обратно, корректные постановки К. з. иногда могут служить основой для классификации типов дифференциальных уравнений.
К. з. наз. линейной, если операторы Lи Влинейны, и однородной, если fи j в (1), (2) равны нулю. Линейная К. з. наз. нётеровой, если: а) однородная задача имеет конечное число kлинейно независимых решений; б) неоднородная задача разрешима тогда и только тогда, когда f и j удовлетворяют lлинейно независимым условиям типа условий ортогональности; в) при условии однозначной разрешимости решение непрерывно зависит от f и j.
Если k=l, то задача наз. фредгольмовой. Разность k-lопределяет индекс задачи. Широкий класс К. з. для линейных уравнений с частными производными 2-го порядка
охватывается задачей Пуанкаре. В этой задаче носителем краевых условий является вся граница, к-рая предполагается ( п-1)-мерным многообразием, а граничный оператор Вв (2) имеет вид
Задача Пуанкаре хорошо исследована в ограниченной области Dс достаточно гладкой границей, при условии равномерной эллиптичности оператора L.
В предположении достаточной гладкости коэффициентов операторов L и В в (3), (4) и границы области Dзадача Пуанкаре нётерова, если 
и фредгольмова, если 
_ и вектор 
некасателен к 5. При исследовании задачи Пуанкаре в двумерном случае широкое применение находят методы теории функций комплексного переменного (см. Краевая задача;методы комплексного переменного).
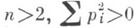
Для общего эллиптич. уравнения порядка 2m
краевые условия могут задаваться с помощью линейных дифференциальных операторов
порядка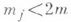 
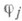
с коэффициентами, определенными на границе Sобласти D. Если операторы Lи В j удовлетворяют так наз. условию дополнительности, то производные порядка 2m функции н, удовлетворяющей граничным условиям, можно оценить (в нек-рой норме) через норму f в (5) и подходящие нормы граничных функций 
в (6). К. з. такого типа наз. коэрцитивными К. з.
Другой тип К. з. представляют так наз. смешанные задачи, в к-рых на смежных участках границы задаются различные краевые условия.
Для эллиптич. уравнений характерно то, что краевые условия задаются на всей границе. Однако в полной мере это относится только к равномерно эллиптич. уравнениям. Если оператор Lв (3) эллиптичен внутри области и на части 
параболически вырождается, то в зависимости от характера вырождения участок S 0 от задания краевых условий может освобождаться. См. также Краевая задача для эллиптического уравнения.
задача Дирихле в области D, ограниченной прямыми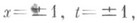 
состоит в задании граничных значений функции ина отрезках 
Специальным образом ставятся К. з. для уравнений смешанного эллиптико-типерболич. типа.
где G(t).и g(t) — заданные функции. С помощью представлений аналитич. функций интегралами типа Коши при некоторых предположениях относительно функций G, gи линии Sрешения этой задачи выписываются в явном виде. См. Граничные задачи теории аналитических функций.
Для изучения К. з. предложен ряд методов. Шварца альтернирующий метод и связанные с ними выметания метод Пуанкаре и Перрона метод опираются на применение принципа максимума. Решение К. з. с помощью интегральных уравнений основано на различных интегральных представлениях решений. Исследование К. з. с помощью априорных оценок относится к функциональным методам. Широко применяется теория обобщенных функций. В практических приложениях значительное распространение получили различные конечноразностные методы.
Лит.: [1] Б е р с Л., Джон Ф., Ш е х т е р М., Уравнения с частными производными, пер. с англ., М., 1966; [2] Бицадзе А. В., Краевые задачи для эллиптических уравнений второго порядка, М., 1966; [3] К у р а н т Р., Уравнения с частными производными, пер. с англ., М., 1964; [4] Ладыженская О. А., Краевые задачи математической физики, М., 1973; [5] М и р а н д а К., Уравнения с частными производными эллиптического типа, пер. с итал., М,, 1957: [6] Мусхелишвили Н. И., Сингулярные интегральные уравнении, 3 изд., М., 1968; [7] Т и х о н о в А. Н., Самарский А. А., Уравнения математической физики, 4 изд., М., 1972.
Краевые задачи
По этой ссылке вы найдёте полный курс лекций по математике:
предыдущих параграфах для уравнения п-го порядка рассматривалась задача с начальными условиями, в конторой все п условий задаются при одном и том же значении t = tQ. В краевой задаче задаются условия при двух (или более) значениях t. Такие условия называются краевыми. Здесь будут рассматриваться только линейные краевые задачи, в которых дифференциальное уравнение и краевые условия линейны. Левые части краевых условий — линейные комбинации значений искомой функции и ее производных в заданных точках ti9 а правые части — заданные постоянные числа.
Примеры линейных краевых условий: возможны и другие виды условий Если постоянная в правой части краевого условия равна нулю, то условие называется однородным, если не равна нулю — неоднородным. Для уравнения п-го порядка задаются п условий. В разных точках t< условия могут быть одного типа или разных типов. Краевая задача называется однородной, если дифференциальное уравнение и краевые условия линейны и однородны.
В отличие от задачи с начальными условиями краевая задача может иметь одно или много решений, а может и не иметь решений. Например, задача имеет единственное решение у = a sin*, а задача случае Ьф 0 не имеет решений (так как все решения уравнения, для которых у(0) = 0, имеют вид у = с sin t и при t = х они равны нулю), а в случае b = 0 имеет бесконечно много решений у = с sin t, с — любое. Теорема 13 (об альтернативе).
Рассмотрим уравнение Краевые задачи. (все a-(t) и f(t) непрерывны, aQ(t) Ф 0) с п линейными краевыми условиями. Возможны только два случая: или 1) задача имеет единственное решение при любых правых частях в уравнении и краевых условиях, или 2) однородная задача (левые части те же, а правые заменяются нулями) имеет бесконечно много решений, а неоднородная задача при некоторых правых частях имеет бесконечно много решений, а при всех других — не имеет решений.
Если данная задача однородна, то правые части алгебраических уравнений равны нулю. Возможны только два следующих случая. 1) Если детерминант системы не равен нулю, то система имеет единственное решение cp. cn при любых правых частях. Подставляя эти ср. сп в (59), получаем единственное решение краевой задачи. 2) Если детерминант системы равен нулю, то однородная система (т. е. при правых частях, равных нулю) имеет бесконечно много решений относительно ср. сп, а неоднородная система имеет решение не при любых правых частях.
Если она имеет решение, то она имеет бесконечно много решений, так как к этому решению можно прибавить любое решение однородной системы, умноженное на любую постоянную. Для любого набора постоянных ср. сп, удовлетворяющего системе, формула (59) дает решение краевой задачи. Для разных наборов сх. сп эти решения различны, так как функции у<9. уп линейно независимы. Из 1) и 2) следует утверждение теоремы. Пример 17.
Найти наименьшее из таких чисел Ь > О, что задача не имеет решений.
Решение примера. По теореме 13 задача (60) не имеет решений тогда, когда однородная задача у» + Ь2у = 0, у(0) = 0, у(1) = О имеет ненулевое решение. Функции, для которых у» + Ь2у = О, у(0) = 0, имеют вид у = с sin bt. Чтобы при с Ф 0 было у(1) = О, надо sin Ь — 0, то есть Ь = тг, 2х, Зх. При этих b имеем 2-й случай альтернативы, значит, при этих b задача (60) или не имеет решений, или имеет бесконечно много решений. Какая из этих возможностей осуществится, надо проверить.
Для каждого 8 = const функция y(t) = G(t, s) при t Ф s удовлетворяет уравнению Ly = 0. 2° При t = tx и t = t2 функция y(t) = G(t, 5) удовлетворяет краевым условиям из (61). 3° При t = 8 она непрерывна по ty а ее производная по t имеет скачок, равный 1 /а0(*), то есть Краевые задачи. Следующая теорема устанавливает условия существования функции Грина и дает способ ее построения.
Так как первому из краевых условий в (61) удовлетворяет только ур а второму — только у2, то из требований Г и 2° вытекает, что функция G должна иметь вид (63). Из требования 3° вытекают уравнения (64). Система (64) разрешима относительно а и Ь, так как ее детерминант равен (решения у,, у2 линейно независимы). Итак, при выполнении условий теоремы найдутся а и Ь, удовлетворяющие (64), а тогда функция (63) удовлетворяет требованиям Замечание.
Возможно вам будут полезны данные страницы:
| Найти функцию Грина краевой задачи |
Теперь из (68) Задачи для упражнений: [12], § 13, № 764-771. |3«| Рассмотрим краевую задачу для уравнения с параметром А где Ly9a9p, 7, б те же, что в (61). Значения А, при которых задача (69) имеет ненулевое решение, называются собственными значениями этой задачи, а сами ненулевые решения — собственными функциями. При тех А, которые являются собственными значениями, имеет место второй случай альтернативы, а при остальных — первый. Пример 19.
Важное направление теории краевых задач — спектральная теория, изучающая свойства собственных значений и собственных функций. Выделен класс «самосопряженных» краевых задач, у которых собственные функции ортогональны в пространстве Ь2 на данном отрезке и доказано, что любую гладкую функцию на этом отрезке, удовлетворяющую краевым условиям этой задачи, можно разложить в сходящийся ряд по собственным функциям такой задачи, аналогичный ряду Фурье [30], гл. 7. Такие разложения используются, в частности, при решении различных задач для уравнений с частными производными методом разделения переменных
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.