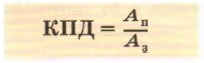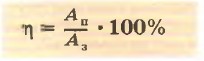что такое кпд рычага
Что такое рычаг? Правило рычага и значение его КПД
Рычаг является простым механизмом, который в настоящее время широко используется в сложных машинах и механических системах. Принцип, согласно которому работает он, называется правилом рычага. Рассмотрим в статье, в чем суть этого правила, а также приведем формулу расчета КПД этого простого механизма.
Рычаг в физике
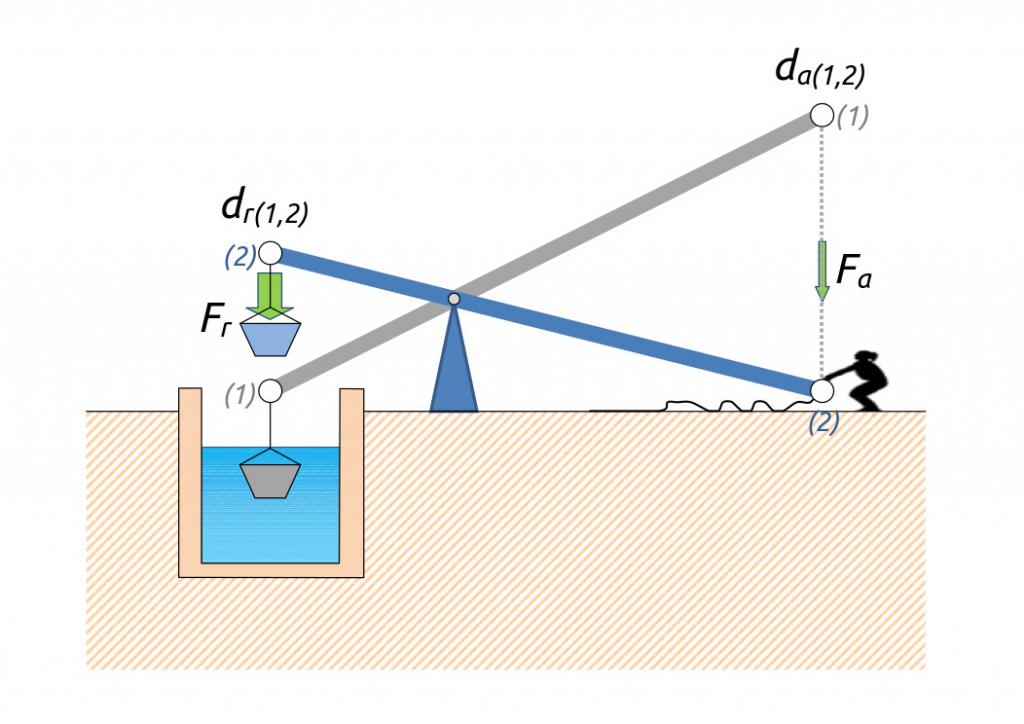
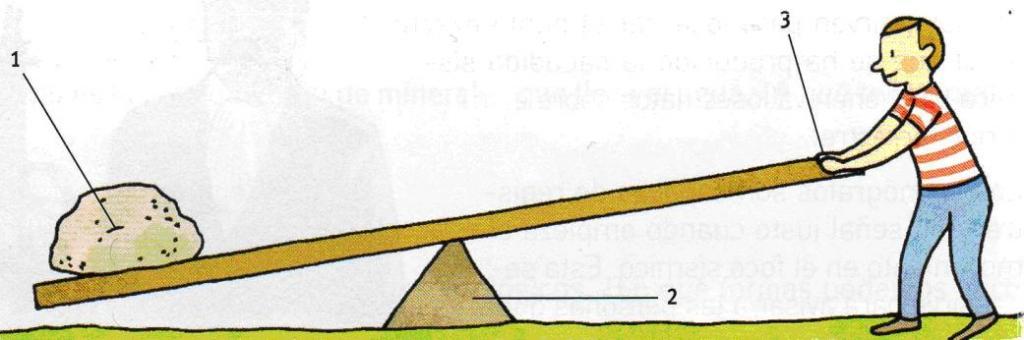
Говоря простыми словами, рычаг представляет собой балку с одной опорой, которая условно разделяет балку на два плеча. Оба плеча способны поворачиваться вокруг опоры за счет действия двух сил. Пример рычага показан ниже.
Этот механизм используется с незапамятных времен для перемещения тяжелых грузов с помощью человеческой силы, а также для сообщения скорости телам, например в катапультах.
Что такое правило рычага?
Под этим правилом понимают соотношение между действующими на рычаг силами и соответствующими длинами плеч. Чтобы математически получить его, введем понятие момента силы. Под моментом силы понимают произведение модуля силы на величину плеча силы. Из статики известно, что если сумма моментов всех сил в системе равна нулю, то такая система вращаться не будет.
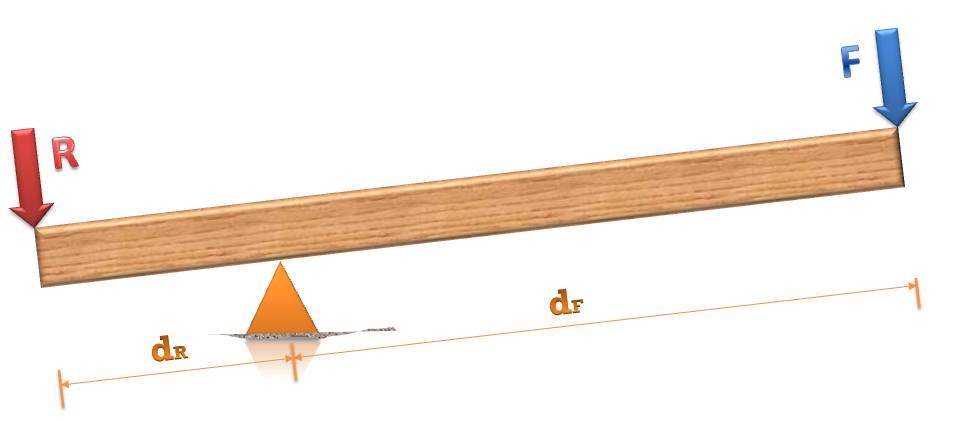
Рассмотрим, какие силы действуют на рычаг, изображенный выше. В первую очередь это внешняя сила F, которая стремится преодолеть силу R и повернуть рычаг по часовой стрелке. В свою очередь, сила R, которая называется нагрузочной, стремится повернуть плечо против часовой стрелки. Поскольку знак момента силы определяется направлением поворота системы вокруг оси вращения, то силы F и R создают моменты разного знака. В случае равенства нулю их суммы получаем:
Это правило рычага, которое экспериментально обнаружил Архимед в III веке до н. э. Согласно данному правилу, чем большая сила приложена к меньшему плечу, тем меньшую силу следует приложить к большему плечу, чтобы система находилась в равновесии.
Когда рычаг совершает поворот вокруг опоры, то меньшее плечо проходит меньший путь (длину дуги), чем большее плечо. Однако такой поворот происходит, когда на большее плечо действует меньшая сила, чем на меньшее. Если dR dF, тогда F>R, и мы получаем выигрыш в пути.
Правило рычага, которое гласит, что любой выигрыш в пути ведет к пропорциональному проигрышу в силе и наоборот, также называется золотым правилом механики.
Коэффициент полезного действия механизма
Часто можно встретить задачи по физике, которые предполагают расчет КПД рычага. Под КПД любого механизма понимают отношения полезной и затраченной работ, то есть:
Как видно из равенства, величину КПД часто выражают в процентах.
Применительно к случаю рычага получаем, что полезная работа связана с преодолением силы сопротивления R, которой может быть вес некоторого тела:
Затраченная работа связана с перемещением плеча dF при воздействии силы F. Она рассчитывается по формуле:
Несложно показать из геометрических соображений, что:
Это означает, что затраченная и полезная работы должны быть равны друг другу, и, как следствие, КПД рычага составит 100 %.
В действительности значение КПД всегда меньше 100 %, поскольку присутствуют различного рода силы трения (трение в воздухе, в оси вращения). В результате трения часть затраченной работы расходуется на нагрев деталей рычага, что приводит к снижению величины полезной работы.
Простые механизмы. КПД рычага. Правило рычага.
Рычаг представляет собой твердое тело, способное вращаться вокруг неподвижной опоры.
Правило рычага гласит:
Рычаг находится в равновесии, если приложенные к нему силы обратно пропорциональны их плечам:
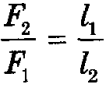
Из формулы 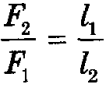
Но F1l1 = М1 — момент силы, стремящейся повернуть рычаг по часовой стрелке, a F2l2 = М2 — : момент силы, стремящейся повернуть рычаг против часовой стрелки. Таким образом, М1 =М2, что и требовалось доказать.
Рычаг начал применяться людьми в глубокой древности. С его помощью удавалось поднимать тяжелые каменные плиты при постройке пирамид в Древнем Египте. Без рычага это было бы невозможно. Ведь, например, для возведения пирамиды Хеопса, имеющей высоту 147 м, было использовано более двух миллионов каменных глыб, самая меньшая из которых имела массу 2,5 тонн!
В наше время рычаги находят широкое применение как на производстве (например, подъемные краны), так и в быту (ножницы, кусачки, весы).
Простые механизмы.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: простые механизмы, КПД механизма.
Рычаг.
 |
| Рис. 1. Рычаг |
Из этого соотношения следует, что рычаг даёт выигрыш в силе или в расстоянии (смотря по тому, с какой целью он используется) во столько раз, во сколько большее плечо длиннее меньшего.
Например, чтобы усилием 100 Н поднять груз весом 700 Н, нужно взять рычаг с отношением плеч 7 : 1 и положить груз на короткое плечо. Мы выиграем в силе в 7 раз, но во столько же раз проиграем в расстоянии: конец длинного плеча опишет в 7 раз большую дугу, чем конец короткого плеча (то есть груз).
Неподвижный блок.
Важной разновидностью рычага является блок — укреплённое в обойме колесо с жёлобом, по которому пропущена верёвка. В большинстве задач верёвка считается невесомой нерастяжимой нитью.
На рис. 2 изображён неподвижный блок, т. е. блок с неподвижной осью вращения (проходящей перпендикулярно плоскости рисунка через точку ).
 |
Зачем же тогда вообще нужен неподвижный блок? Он полезен тем, что позволяет изменить направление усилия. Обычно неподвижный блок используется как часть более сложных механизмов.
Подвижный блок.
 |
Следовательно, подвижный блок даёт выигрыш в силе в два раза. При этом, однако, мы в те же два раза проигрываем в расстоянии: чтобы поднять груз на один метр, точку придётся переместить на два метра (то есть вытянуть два метра нити).
 |
Принципиально данное устройство ничем не отличается от подвижного блока: с его помощью мы также получаем двукратный выигрыш в силе.
Наклонная плоскость.
Как мы знаем, тяжёлую бочку проще вкатить по наклонным мосткам, чем поднимать вертикально. Мостки, таким образом, являются механизмом, который даёт выигрыш в силе.
 |
Выберем ось так, как показано на рисунке. Поскольку груз движется без ускорения, действующие на него силы уравновешены:
Проектируем на ось :
Именно такую силу нужно приложить, что двигать груз вверх по наклонной плоскости.
Широко применяемыми разновидностями наклонной плоскости являются клин и винт.
Золотое правило механики.
Простой механизм может дать выигрыш в силе или в расстоянии, но не может дать выигрыша в работе.
т. е. той же величине, что и без использования рычага.
т. е. ту же самую, что и при вертикальном поднятии груза.
Данные факты служат проявлениями так называемого золотого правила механики.
Золотое правило механики. Ни один из простых механизмов не даёт выигрыша в работе. Во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии, и наоборот.
Золотое правило механики есть не что иное, как простой вариант закона сохранения энергии.
КПД механизма.
На практике приходится различать полезную работу A полезн, которую нужно совершить при помощи механизма в идеальных условиях отсутствия каких-либо потерь, и полную работу Aполн,
которая совершается для тех же целей в реальной ситуации.
Полная работа равна сумме:
-полезной работы;
-работы, совершённой против сил трения в различных частях механизма;
-работы, совершённой по перемещению составных элементов механизма.
Так, при подъёме груза рычагом приходится вдобавок совершать работу по преодолению силы трения в оси рычага и по перемещению самого рычага, имеющего некоторый вес.
Полная работа всегда больше полезной. Отношение полезной работы к полной называется коэффициентом полезного действия (КПД) механизма:
КПД принято выражать в процентах. КПД реальных механизмов всегда меньше 100%.
 |
Ускорения нет, поэтому силы, действующие на груз, уравновешены:
Проектируем на ось X:
Проектируем на ось Y:
Полная работа равна произведению силы F на путь, пройденный телом вдоль поверхности наклонной плоскости:
§ 65. Коэффициент полезного действия механизма
Рассматривая устройство и действие рычага, мы не учитывали трение, а также вес рычага. В этих идеальных условиях работа, совершённая приложенной силой (эту работу мы будем называть полной), равна полезной работе по подъёму грузов или преодолению какого- либо сопротивления.
На практике совершённая с помощью механизма полная работа всегда несколько больше полезной работы.
Часть работы совершается против силы трения в механизме и по перемещению его отдельных частей. Так, применяя подвижный блок, приходится дополнительно совершать работу по подъёму самого блока, верёвки и по преодолению силы трения в оси блока.
Какой бы механизм мы ни взяли, полезная работа, совершённая с его помощью, всегда составляет лишь часть полной работы. Следовательно, обозначив полезную работу буквой Ап, а полную (затраченную) — буквой Аз, можно записать:
Сокращённо коэффициент полезного действия обозначается КПД.
КПД обычно выражают в процентах и обозначают греческой буквой η (читается «эта»):
П р и м е р. На коротком плече рычага подвешен груз массой 100 кг. Для его подъёма к длинному плечу приложили силу 250 Н. Груз подняли на высоту h1 = 0,08 м, при этом точка приложения движущей силы опустилась на высоту h2 = 0,4 м. Найти коэффициент полезного действия рычага.
Запишем условие задачи и решим её.
Но «золотое правило» механики выполняется и в этом случае. Часть полной работы — 20% её — расходуется на преодоление трения в оси рычага и сопротивления воздуха, а также на движение самого рычага.
Вопросы
1. Какую работу называют полезной, какую — полной?
2. Почему при применении механизмов для подъёма грузов и преодоления какого-либо сопротивления полезная работа не равна полной?
3. Что такое коэффициент полезного действия механизма?
4. Может ли коэффициент полезного действия быть больше единицы? Ответ обоснуйте.
5. Как можно увеличить коэффициент полезного действия?
Что такое кпд рычага
При перемещении тела с помощью простых механизмов (рычагов, блоков, наклонной плоскости) приложенной силе приходится преодолевать не только вес самого груза.
Надо поднять груз с помощью подвижного блока на высоту.
Для поднятия груза человек прикладывает к веревке силу (F тяги).
Какую работу он при этом совершает?
Надо поднять непосредственно груз весом Р.
Кроме груза надо поднять еще веревку и блок весом Р бл.
Надо преодолеть трение о воздух и в осях блока, мешающее подьему.
1. Какую работу называют полной?
1. Какую работу называют полезной?
Совершаемая с помощью механизма полная работа всегда больше полезной работы.
Часть затрачиваемой работы расходуется на преодоление трения в оси механизма и сопротивления воздуха, а также на движение самого механизма.
3. Что такое коэффициент полезного действия механизма?
Отношение полезной работы к полной работе называется коэффициентом полезного действия.
Сокращенно коэффициент полезного действия обозначается КПД.
КПД обычно выражают числом или в процентах и обозначают греческой буквой, которая читается как «эта».
4. Может ли КПД быть больше единицы?
Полезная работа всегда меньше затраченной работы.
Поэтому КПД любого механизма всегда меньше 100% ( или меньше 1).
Конструируя механизмы, стремятся увеличить их КПД. Для этого уменьшают трение в осях механизмов и их вес.
4. Пример решения задачи на расчет КПД.
Задача.
На коротком плече рычага подвешен груз массой 100 кг.
Для его подъема к длинному плечу приложили силу 250 Н.
Груз подняли на высоту h1 = 0,08 м, при этом точка приложения движущей силы опустилась на высоту h2 = 0,4 м.
Найти КПД рычага.