что такое ковариация в теории вероятностей
Ковариация случайных величин
Содержание
Вычисление [ править ]
В силу линейности математического ожидания, ковариация может быть записана как:
Свойства ковариации [ править ]
Неравенство Коши — Буняковского [ править ]
Докажем три аксиомы скалярного произведения:
[math] \mathrm Для этого предположим, что [math] t [/math] — некоторое вещественное число, и рассмотрим очевидное неравенство Используя линейность математического ожидания, мы получаем такое неравенство: [math] E(V^2)+2 \cdot t \cdot E(V \cdot W)+t^2 \cdot E(W^2) \geqslant 0 [/math] Итак, наш квадратный трехчлен выглядит следующим образом: [math]\sigma_\xi ^2 \cdot t^2+2 \cdot \mathrm [math] 4 \cdot \mathrm [math]\mathrm [math]\mathrm Матрица ковариаций (англ. covariance matrix) — это матрица, элементы которой являются попарными ковариациями элементов одного или двух случайных векторов. Ковариационная матрица случайного вектора — квадратная симметрическая неотрицательно определенная матрица, на диагонали которой располагаются дисперсии компонент вектора, а внедиагональные элементы — ковариации между компонентами. Например, ковариационная матрица для случайного вектора [math]\xi[/math] выглядит следующим образом: Расстояние Махаланобиса (англ. Mahalanobis distance) — мера расстояния между векторами случайных величин, обобщающая понятие евклидова расстояния. Расстояние Махаланобиса двух случайных векторов [math]\xi, \eta[/math] с матрицей ковариации [math]\Sigma[/math] — это мера различия между ними. Если матрица ковариации равняется единичной матрице, то расстояние Махалонобиса равняется расстоянию Евклида. которая может быть получена из первой формулы, используя свойства математического ожидания. Перечислим основные свойства ковариации. 1. Ковариация случайной величины с самой собой есть ее дисперсия. 2. Ковариация симметрична. $$cov\left(X,\ Y\right)=cov\left(Y,\ X\right).$$ 4. Постоянный множитель можно выносить за знак ковариации. $$cov\left(cX,\ Y\right)=cov\left(X,\ cY\right)=c\cdot cov\left(X,\ Y\right).$$ 5. Ковариация не изменится, если к одной из случайных величин (или двум сразу) прибавить постоянную величину: $$cov\left(X+c,\ Y\right)=cov\left(X,\ Y+c\right)=cov\left(X+x,\ Y+c\right)=cov\left(X,\ Y\right).$$ 9. Дисперсия суммы (разности) случайных величин равна сумме их дисперсий плюс (минус) удвоенная ковариация этих случайных величин: $$D\left(X\pm Y\right)=D\left(X\right)+D\left(Y\right)\pm 2cov\left(X,\ Y\right).$$ $$M\left(X\right)=\sum^n_ $$M\left(Y\right)=\sum^n_ $$M\left(XY\right)=\sum_ Перечислим основные свойства коэффициента корреляции. При копировании материала с сайта, обратная ссылка обязательна! Спектральные методы — это класс техник, используемых в прикладной математике для численного решения некоторых дифференциальных уравнений, возможно, вовлекая Быстрое преобразование Фурье. Идея заключается в переписи решения дифференциальных уравнений как суммы некоторых «базисных функций» (например, как ряды Фурье являются суммой синусоид), а затем выбрать коэффициенты в сумме, чтобы удовлетворить дифференциальному уравнению, насколько это возможно. О дискретном эквиваленте преобразования Лапласа см. Z-преобразование.В математике дискретный оператор Лапласа — аналог непрерывного оператора Лапласа, определяемого как отношения на графе или дискретной сетке. В случае конечномерного графа (имеющего конечное число вершин и рёбер) дискретный оператор Лапласа имеет более общее название: матрица Лапласа. В вычислительной математике одной из наиболее важных задач является создание эффективных и устойчивых алгоритмов нахождения собственных значений матрицы. Эти алгоритмы вычисления собственных значений могут также находить собственные векторы. В теории вероятностей случайная величина имеет дискретное равномерное распределение, если она принимает конечное число значений с равными вероятностями. В теории вероятностей два случайных события называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. Аналогично, две случайные величины называют независимыми, если известное значение одной из них не дает информации о другой. Конечная разность — математический термин, широко применяющийся в методах вычисления при интерполировании. Центра́льные преде́льные теоре́мы (Ц. П. Т.) — класс теорем в теории вероятностей, утверждающих, что сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному. Здравствуйте, уважаемые читатели проекта Тюлягин! Сегодня речь пойдет о дисперсии и ковариации, двух на первый взгляд сложных понятий. Однако при более близком рассмотрении вы поймете что в них нет ничего сложного. Эти два термина чаще всего можно встретить в математике и статистике, однако они также используются в финансах и инвестициях. Об этом и поговорим далее в статье. Содержание статьи: Дисперсия и ковариация — математические термины, часто используемые в статистике и теории вероятностей. Дисперсия это разброс набора данных вокруг его среднего значения, в то время как ковариация это мера направленного отношения между двумя случайными величинами. В дополнение к их общему использованию в статистике, оба этих термина имеют также определенные значения для инвесторов, относящиеся к измерениям, проводимым на фондовом рынке, и распределению активов, оба из которых указаны ниже. Дисперсия используется в статистике для описания разброса между набором данных от его среднего значения. Она рассчитывается путем нахождения взвешенного по вероятности среднего квадрата отклонений от ожидаемого значения. Таким образом, чем больше дисперсия, тем больше расстояние между числами в наборе и средним значением. И наоборот, меньшая дисперсия означает, что числа в наборе ближе к среднему. Наряду со статистическим определением термин дисперсия также может использоваться в финансовом контексте. Многие биржевые эксперты и финансовые консультанты используют дисперсию акции для измерения ее волатильности. Возможность выразить, насколько далеко стоимость данной акции может отклониться от среднего значения, в одном числе — очень полезный индикатор того, насколько велик риск, с которым связана конкретная акция. Акция с более высокой дисперсией обычно сопряжена с большим риском и потенциалом для более высокой или более низкой доходности, в то время как акция с меньшей дисперсией может быть менее рискованной, что означает, что она будет иметь среднюю доходность. Ковариация — это мера того, как две случайные величины изменятся при сравнении друг с другом. Однако в финансовом или инвестиционном контексте термин ковариация описывает доходность двух разных инвестиций за период времени по сравнению с разными переменными. Эти активы обычно представляют собой рыночные ценные бумаги в портфеле инвестора, например акции. Положительная ковариация означает, что доходность обоих инвестиций имеет тенденцию одновременно увеличиваться или уменьшаться в стоимости. С другой стороны, обратная или отрицательная ковариация означает, что доходности будут отдаляться друг от друга. Так, когда один актив поднимается, другой актив падает. Ковариация может измерять движения двух переменных, но не указывает на степень, в которой эти две переменные изменяются по отношению друг к другу. А на этом сегодня все про дисперсию и ковариацию, как видите это не так и сложно. Надеюсь статья была для вас полезной и интересной. Делитесь статьей в социальных сетях и мессенджерах и добавляйте сайт в закладки. Успехов и до новых встреч на страницах проекта Тюлягин! Повторение статистики для начала путешествия по науке о данных Предположим, у нас есть диаграмма рассеяния, на которой каждая точка — это человек. На одной оси показан его профессиональный опыт в годах, на другой — доход. В соответствии с диаграммой справа можно заключить, что между опытом и доходом нет никакой связи, то есть определенный опыт оплачивается по-разному. Слева, наоборот, между признаками существует четкая линейная зависимость. Ковариация и корреляция показывают, насколько тесно между собой связаны переменные набора данных. N.B: в приведенном примере представлен двумерный вид данных (с двумя переменными). На практике статистики используют многомерные данные (со множеством переменных). Ковариация — это мера зависимости между двумя или более случайных переменных. С английского «covariance» = «co» (совместность/соединение) + «variance» (дисперсия). То есть ковариация похожа на дисперсию, но она применяется для сравнения двух переменных, где вместо суммы квадратов, мы получаем сумму векторного произведения. Ковариация измеряет дисперсию между двумя переменными. Ковариация может быть отрицательной, положительной и нулевой: положительное значение показывает, что две переменные изменяются в одном направлении (если одна переменная увеличивается, то и вторая тоже увеличивается); отрицательное значение показывает, что две переменные изменяются в разных направлениях (одна увеличивается, вторая уменьшается); нулевая ковариация означает, что они изменяются независимо друг от друга. Формулу сложно объяснить, но важно понять, что она означает: Предположим, что набор данных со случайными переменными представлен в виде вектора. Тогда в прошлом примере у нас есть два вектора для опыта и дохода. Ниже приведен порядок действий: На втором этапе измеряется угол между двумя векторами. Если угол острый, то переменные тесно связаны между собой. Следует отметить, что несмотря на то, что ковариация измеряет зависимость между направлениями двух переменных, она не показывает тесноту этой зависимости. На практике самая большая проблема с этой мерой заключается в том, что она зависит от используемой единицы измерения. Например, необходимо перевести годы опыта в месяцы. Тогда ковариация будет в 12 раз больше. В этом случае на помощь приходит корреляция! Корреляция — одна из наиболее распространенных мер в статистике, описывающая тесноту взаимосвязи между двумя случайными переменными. Она считается нормализованной версией ковариации. Давайте рассмотрим, почему… Корреляция (обозначаемая греческой буквой «ро» — ρ) рассчитывается по следующей формуле: Обратите внимание, что функциональная связь редко встречается на практике, так как две случайные переменные обычно не сопоставляются друг с другом на основе постоянного значения. Корреляция, равная 0, означает, что между двумя переменными нет линейной зависимости. Тогда может быть отношение x = y². Корреляция — безразмерная величина, указывающая не только на направление взаимосвязи, но и на ее тесноту (в зависимости от того, насколько большим является абсолютное значение). Единицы измерения исключены из-за того, что ковариацию разделили на среднеквадратическое отклонение. Напоследок необходимо запомнить, что корреляция не является причинно-следственной связью. Высокая корреляция между двумя случайными переменными просто означает, что они связаны друг с другом, но их взаимоотношение не обязательно должен иметь причинно-следственный характер. Доказать причинно-следственную связь можно только с помощью контролируемых экспериментов, при которых внешние переменные исключаются и эффекты двух данных переменных изолируются.[math]\triangleleft[/math] Теорема (неравенство Коши — Буняковского): [math]\triangleleft[/math] Матрица ковариаций [ править ]
Расстояние Махаланобиса [ править ]
Ковариация
Корреляция
Ковариация
Связанные понятия
Упоминания в литературе
Связанные понятия (продолжение)
Дисперсия и ковариация: что это такое и в чем разница?
Что такое дисперсия и ковариация
Дисперсия простыми словами
Ковариация простыми словами
Ковариацию также можно использовать как инструмент для диверсификации портфеля инвестора. Для этого управляющий инвестиционным портфелем должен искать инвестиции, которые имеют отрицательную ковариацию друг с другом. Это означает, что когда доходность одного актива падает, доходность другого (связанного) актива повышается. Таким образом, покупка акций с отрицательной ковариацией — отличный способ минимизировать риск портфеля. Можно ожидать, что экстремальные пики и спады динамики акций уравновесят друг друга, что приведет к более стабильной норме доходности на протяжении многих лет.Резюме
Введение
Ковариация
Дисперсия показывает, насколько определенная переменная отличается от среднего значения, а ковариация — насколько две переменные отличаются друг от друга. Таким образом, можно утверждать следующее:Формула
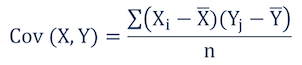
Ограниченность
Корреляция
Формула
Ключевые свойства

