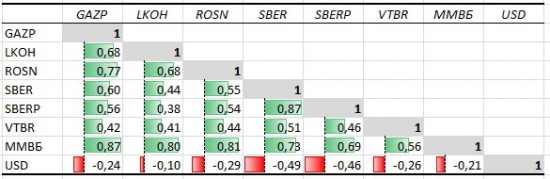
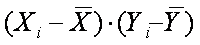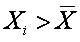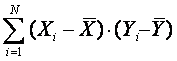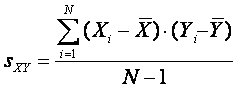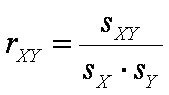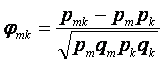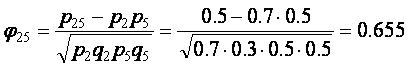что такое корреляционная матрица

как построить корреляционную матрицу (для парной торговли)

Для эффективной парной торговли очень важно знать коэффициенты корреляции между инструментами.

Сегодня мы по пунктам разберем, как построить корреляционную матрицу в экселе за 5 минут.

Пример корреляционной матрицы:

Алгоритм построения:
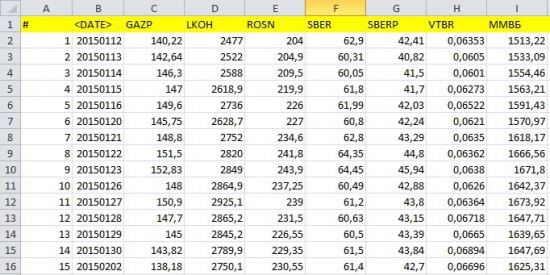
1. Скачиваем исторические дневные данные (минимум за 1 год). я пользуюсь сайтом финама (раздел экспорт данных) http://www.finam.ru/profile/moex-akcii/gazprom/export/

2. Вставляем все скаченные данные в эксель

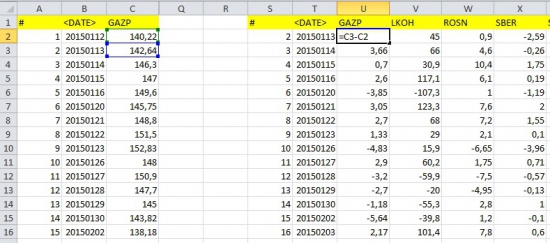
3. Находим разность между (динамику изменения котировок день/день

4. Настраиваем в экселе Data Analysis (Файл-параметры-надстройки-перейти-выделяем галочкой все пункты). далее во вкладке данные у нас появляется функция Data Analysis

5.Далее выделяем все колонки с разностью и нажимаем на кнопку Data Analysis

6. Следующим пунктом выбираем Correlation

7. И в итоге у нас получается вот такая корреляционная матрица

если будут вопросы, пишите их в комментариях

Источник

Что такое корреляционная матрица

Если две величины связаны между собой, то между ними есть корреляция. Виды корреляционной связи показаны в таблице 3.9.

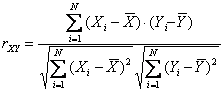
Для выяснения вопроса о наличии связи между двумя величинами X и Y необходимо определить, существует ли соответствие между большими и малыми значениями X и соответствующими значениями Y или такой связи не обнаруживается. Значение каждого элемента X_i и Y_i определяется величиной и знаком отклонения от среднего арифметического 11 :

Если большие значения X_i соответствуют большим значениям Y_i, то это произведение будет большим и положительным, так как

и

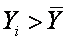
То же самое будет наблюдаться и, когда малые значения X_i будут соответствовать малым Y_i, поскольку произведение отрицательных чисел будет положительным.

Если же большие значения X_i соответствуют малым значениям Y_i, то это произведение будет большим и отрицательным, что будет свидетельствовать об обратной зависимости между этими величинами.

В тех случаях, когда нет систематического соответствия больших значений X_i большим или малым Y_i, то знак произведения будет положительным или отрицательным для разных пар X_i и Y_i. Тогда сумма

Для того, чтобы эта сумма не зависела от количества значений X и Y, ее следует поделить ее на N-1. Полученная величина s_XY называется ковариацией X и Y и является мерой их связи:

Для исключения влияния стандартных отклонений на величину связи, следует поделить ковариацию s_XY на стандартные отклонения s_X и s_Y:

Полученная мера связи между X и Y называется коэффициентом корреляции Пирсона. Обозначение r происходит от слова регрессия. Подставив соответствующие выражения, получим формулу для коэффициента корреляции Пирсона r_XY 11

Для вычислений более удобна следующая формула

Следует отметить, что в случае нелинейной связи между X и Y коэффициент корреляции может оказаться близким к нулю, даже если связь очень сильная.

Таблица 3.7.1. Типы корреляционной связи

(Гласс Дж., Стэнли Дж., 1976).

Для решения вопроса о наличии связи между заданиями теста, надо, используя данные по столбцам из бинарной матрицы, рассчитать коэффициенты корреляции Пирсона для каждой пары заданий. Для расчетов используются различные статистические программы (SPSS, STATISTICA и др.). В простейшем случае можно использовать табличный процессор Excel с вызовом функции «ПИРСОН».

p_m – доля верных ответов для задания с номером m;
q_m – доля неверных ответов для задания с номером m;
p_k – доля верных ответов для задания k;
q_k – доля неверных ответов для задания с номером k;
p_mk – доля верных ответов для задания с номером m и k.

Коэффициент корреляции Пирсона, для дихотомических данных называется коэффициентом «фи». Коэффициент φ_mk, описывающий связь между заданиями с номерами m и k записывается следующим образом 11

Отметим, что коэффициент «фи» и коэффициент корреляции Пирсона дают в результате одно и то же значение, поскольку обе формулы эквивалентны. Рассмотрим пример вычисления коэффициента корреляции между 2-м и 5-м заданиями. Из таблицы 3.2.5 имеем: p₂=0.7, q₂=0.3, p₅=0.5, q₅=0.5. Для определения p₂₅ надо подсчитать количество верных ответов на оба задания одновременно. Видно, что испытуемые с номерами 1-5 успешно справились с обоими заданиями (5 верных ответов). Испытуемые 6 и 7 правильно ответили на 2-е задание, но неправильно на 5-е (нет одновременно верных ответов). Испытуемые 8 и 9 не справились и со 2-м и с 5-м заданиями. Таким образом, p₂₅ =5/10 = 0,5.

Результаты расчетов для всех заданий приведены в корреляционной матрице (таблица 3.7.2). Корреляционная матрица представляет собой квадратную матрицу размерности MxM, где M – количество заданий, симметричную относительно главной диагонали. В нашем примере матрица имеет 8 строк и столько же столбцов. Коэффициент корреляции Пирсона, скажем, между 2-м и 5-м заданиями находится на пересечении 2-й строки и 5-го столбца (0,655).

В самом последнем столбце располагается коэффициент корреляции каждого задания с тестовым баллом испытуемого (индивидуальным баллом) – r_pb – точечный бисериальный коэффициент корреляции.

ТАБЛИЦА 3.7.2. Корреляционная матрица тестовых заданий.

Источник

Корреляция, ковариация и девиация (часть 3)

В первой части показано, как на основе матрицы расстояний между элементами получить матрицу Грина. Ее спектр образует собственную систему координат множества, центром которой является центроид набора. Во второй рассмотрены спектры простых геометрических наборов.

В данной статье покажем, что матрица Грина и матрица корреляции — суть одно и то же.

7. Векторизация и нормирование одномерных координат

Пусть значения некой характеристики элементов заданы рядом чисел . Для того, чтобы данный набор можно было сравнивать с другими характеристиками, необходимо его векторизовать и обезразмерить (нормировать).
Для векторизации находим центр (среднее) значений

и строим новый набор как разность между исходными числами и их центроидом (средним):

Получили вектор. Основной признак векторов состоит в том, что сумма их координат равна нулю. Далее нормируем вектор, — приведем сумму квадратов его координат к 1. Для выполнения данной операции нам нужно вычислить эту сумму (точнее среднее):

Теперь можно построить ССК исходного набора как совокупность собственного числа S и нормированных координат вектора:

Квадраты расстояний между точками исходного набора определяются как разности квадратов компонент собственного вектора, умноженные на собственное число. Обратим внимание на то, что собственное число S оказалось равно дисперсии исходного набора (7.3).

Итак, для любого набора чисел можно определить собственную систему координат, то есть выделить значение собственного числа (она же дисперсия) и рассчитать координаты собственного вектора путем векторизации и нормирования исходного набора чисел. Круто.

Упражнение для тех, кто любит «щупать руками». Построить ССК для набора <1, 2, 3, 4>.

8. Векторизация и ортонормирование многомерных координат

Что, если вместо набора чисел нам задан набор векторов — пар, троек и прочих размерностей чисел. То есть точка (узел) задается не одной координатой, а несколькими. Как в этом случае построить ССК? Стандартный путь следующий.

Введем обозначение характеристик (компонент) набора. Нам заданы точки (элементы) и каждой точке соответствует числовое значение характеристики . Обращаем внимание, что второй индекс — это номер характеристики (столбцы матрицы), а первый индекс — номер точки (элемента) набора (строки матрицы).

Далее векторизуем характеристики. То есть для каждой находим центроид (среднее значение) и вычитаем его из значения характеристики:

Получили матрицу координат векторов (МКВ) .
Следующим шагом как будто бы надо вычислить дисперсию для каждой характеристики и их нормировать. Но хотя таким образом мы действительно получим нормированные векторы, нам-то нужно, чтобы эти векторы были независимыми, то есть ортонормированными. Операция нормирования не поворачивает вектора (а лишь меняет их длину), а нам нужно развернуть векторы перпендикулярно друг другу. Как это сделать?

Правильный (но пока бесполезный) ответ — рассчитать собственные вектора и числа (спектр). Бесполезный потому, что мы не построили матрицу, для которой можно считать спектр. Наша матрица координат векторов (МКВ) не является квадратной — для нее собственные числа не рассчитаешь. Соответственно, надо на основе МКВ построить некую квадратную матрицу. Это можно сделать умножением МКВ на саму себя (возвести в квадрат).

Но тут — внимание! Неквадратную матрицу можно возвести в квадрат двумя способами — умножением исходной на транспонированную. И наоборот — умножением транспонированной на исходную. Размерность и смысл двух полученных матриц — разный.

Умножая МКВ на транспонированную, мы получаем матрицу корреляции:

Из данного определения (есть и другие) следует, что элементы матрицы корреляции являются скалярными произведениями векторов (грамиан на векторах). Значения главной диагонали отражают квадрат длины данных векторов. Значения матрицы не нормированы (обычно их нормируют, но для наших целей этого не нужно). Размерность матрицы корреляции совпадает с количеством исходных точек (векторов).

Теперь переставим перемножаемые в (8.1) матрицы местами и получим матрицу ковариации (опять же опускаем множитель 1/(1-n), которым обычно нормируют значения ковариации):

Здесь результат выражен в характеристиках. Соответственно, размерность матрицы ковариации равна количеству исходных характеристик (компонент). Для двух характеристик матрица ковариации имеет размерность 2×2, для трех — 3×3 и т.д.

Почему важна размерность матриц корреляции и ковариации? Фишка в том, что поскольку матрицы корреляции и ковариации происходят из произведения одного и того же набора векторов, то они имеют один и тот же набор собственных чисел, один и тот же ранг (количество независимых размерностей) матрицы. Как правило, количество векторов (точек) намного превышает количество компонент. Поэтому о ранге матриц судят по размерности матрицы ковариации.

Диагональные элементы ковариации отражают дисперсию компонент. Как мы видели выше, дисперсия и собственные числа тесно связаны. Поэтому можно сказать, что в первом приближении собственные числа матрицы ковариации (а значит, и корреляции) равны диагональным элементам (а если межкомпонентная дисперсия отсутствует, то равны в любом приближении).

Если стоит задача найти просто спектр матриц (собственные числа), то удобнее ее решать для матрицы ковариации, поскольку, как правило, их размерность небольшая. Но если нам необходимо найти еще и собственные вектора (определить собственную систему координат) для исходного набора, то необходимо работать с матрицей корреляции, поскольку именно она отражает скалярное произведение векторов.

Отметим, что метод главных компонент как раз и состоит в расчете спектра матрицы ковариации/корреляции для заданного набора векторных данных. Найденные компоненты спектра располагаются вдоль главных осей эллипсоида данных. Из нашего рассмотрения это вытекает потому, что главные оси — это и есть те оси, дисперсия (разброс) данных по которым максимален, а значит, и максимально значение спектра.

Правда, могут быть и отрицательные дисперсии, и тогда аналогия с эллипсоидом уже не очевидна.

9. Матрица Грина — это матрица корреляции векторов

Рассмотрим теперь ситуацию, когда нам известен не набор чисел, характеризующих точки (элементы), а набор расстояний между точками (причем между всеми). Достаточно ли данной информации для определения ССК (собственной системы координат) набора?

Ответ дан в первой части — да, вполне. Здесь же мы покажем, что построенная по формуле (1.3′) матрица Грина и определенная выше матрица корреляции векторов (8.1) — это одна и та же матрица.

Как такое получилось? Сами в шоке. Чтобы в этом убедиться, надо подставить выражение для элемента матрицы квадратов расстояний

в формулу преобразования девиации:

Отметим, что среднее значение матрицы квадратов расстояний отражает дисперсию исходного набора (при условии, что расстояния в наборе — это сумма квадратов компонент):

Подставляя (9.1) и (9.3) в (9.2), после несложных сокращений приходим к выражению для матрицы корреляции (8.1):

Итак, матрица Грина и матрица корреляции векторов — суть одно и то же. Ранг матрицы корреляции совпадает с рангом матрицы ковариации (количеством характеристик — размерностью пространства). Это обстоятельство позволяет строить спектр и собственную систему координат для исходных точек на основе матрицы расстояний.

Для произвольной матрицы расстояний потенциальный ранг (количество измерений) на единицу меньше количества исходных векторов. Расчет спектра (собственной системы координат) позволяет определить основные (главные) компоненты, влияющие на расстояния между точками (векторами).

Таким образом можно строить собственные координаты элементов либо на основании их характеристик, либо на основании расстояний между ними. Например, можно определить собственные координаты городов по матрице расстояний между ними.

Источник

Корреляции для начинающих

Апдейт для тех, кто сочтет статью полезной и занесет в избранное. Есть приличный шанс, что пост уйдет в минуса, и я буду вынужден унести его в черновики. Сохраняйте копию!

Краткий и несложный материал для неспециалистов, рассказывающий в наглядной форме о различных методах поиска регрессионных зависимостей. Это все и близко не академично, зато надеюсь что понятно. Прокатит как мини-методичка по обработке данных для студентов естественнонаучных специальностей, которые математику знают плохо, впрочем как и автор. Расчеты в Матлабе, подготовка данных в Экселе — так уж повелось в нашей местности

Введение

Зачем это вообще надо? В науке и около нее очень часто возникает задача предсказания какого-то неизвестного параметра объекта исходя из известных параметров этого объекта (предикторов) и большого набора похожих объектов, так называемой учебной выборки. Пример. Вот мы выбираем на базаре яблоко. Его можно описать такими предикторами: красность, вес, количество червяков. Но как потребителей нас интересует вкус, измеренный в попугаях по пятибалльной шкале. Из жизненного опыта нам известно, что вкус с приличной точностью равен 5*красность+2*вес-7*количество червяков. Вот про поиск такого рода зависимостей мы и побеседуем. Чтобы обучение пошло легче, попробуем предсказать вес девушки исходя из ее 90/60/90 и роста.

Исходные данные

В качестве объекта исследования возьму данные о параметрах фигуры девушек месяца Плейбоя. Источник — www.wired.com/special_multimedia/2009/st_infoporn_1702, слегка облагородил и перевел из дюймов в сантиметры. Вспоминается анекдот про то, что 34 дюйма — это как два семнадцатидюймовых монитора. Также отделил записи с неполной информацией. При работе с реальными объектами их можно использовать, но сейчас они нам только мешают. Зато их можно использовать для проверки адекватности полученных результатов. Все данные у нас непрерывные, то есть грубо говоря типа float. Они приведены к целым числам только чтобы не загромождать экран. Есть способы работы и с дискретными данными — в нашем примере это например может быть цвет кожи или национальность, которые принимают одно из фиксированного набора значений. Это больше имеет отношение к методам классификации и принятия решений, что тянет еще на один мануал. Data.xls В файле два листа. На первом собственно данные, на втором — отсеянные неполные данные и набор для проверки нашей модели.

Обозначения

W — вес реальный
W_p — вес, предсказанный нашей моделью
S — бюст
T — талия
B — бедра
L — рост
E — ошибка модели

Как оценить качество модели?

Задача нашего упражнения — получить некую модель, которая описывает какой-либо объект. Способ получения и принцип работы конкретной модели нас пока не волнует. Это просто функция f(S, T, B, L), которая выдает вес девушки. Как понять, какая функция хорошая и качественная, а какая не очень? Для этого используется так называемая fitness function. Самая классическая и часто используемая — это сумма квадратов разницы предсказанного и реального значения. В нашем случае это будет сумма (W_p — W)^2 для всех точек. Собственно, отсюда и пошло название «метод наименьших квадратов». Критерий не лучший и не единственный, но вполне приемлемый как метод по умолчанию. Его особенность в том, что он чувствителен по отношению к выбросам и тем самым, считает такие модели менее качественными. Есть еще всякие методы наименьших модулей итд, но сейчас нам это пока не надо.

Простая линейная регрессия

Самый простой случай. У нас одна переменная-предиктор и одна зависимая переменная. В нашем случае это может быть например рост и вес. Нам надо построить уравнение W_p = a*L+b, т.е. найти коэффициенты a и b. Если мы проведем этот расчет для каждого образца, то W_p будет максимально совпадать с W для того же образца. То есть у нас для каждой девушки будет такое уравнение:
W_p_i = a*L_i+b
E_i = (W_p-W)^2

Общая ошибка в таком случае составит sum(E_i). В результате, для оптимальных значений a и b sum(E_i) будет минимальным. Как же найти уравнение?

Матлаб

Графичек

Мда, негусто. Это график W_p(W). Формула на графике показывает связь W_p и W. В идеале там будет W_p = W*1 + 0. Вылезла дискретизация исходных данных — облако точек клетчатое. Коэффициент корреляции ни в дугу — данные слабо коррелированы между собой, т.е. наша модель плохо описывает связь веса и роста. По графику это видно как точки, расположенные в форме слабо вытянутого вдоль прямой облака. Хорошая модель даст облако растянутое в узкую полосу, еще более плохая — просто хаотичный набор точек или круглое облако. Модель необходимо дополнить. Про коэффициент корреляции стоит рассказать отдельно, потому что его часто используют абсолютно неправильно.

Расчет в матричном виде

Мультилинейная регрессия

Попытка номер два

А так получше, но все равно не очень. Как видим, клетчатость осталась только по горизонтали. Никуда не денешься, исходные веса были целыми числами в фунтах. То есть после конверсии в килограммы они ложатся на сетку с шагом около 0.5. Итого финальный вид нашей модели:

W_p = 0.2271*S + 0.1851*T + 0.3125*B + 0.3949*L — 72.9132

Объемы в сантиметрах, вес в кг. Поскольку у нас все величины кроме роста в одних единицах измерения и примерно одного порядка по величине (кроме талии), то мы можем оценить их вклады в общий вес. Рассуждения примерно в таком духе: коэффициент при талии самый маленький, равно как и сами величины в сантиметрах. Значит, вклад этого параметра в вес минимален. У бюста и особенно у бедер он больше, т.е. сантиметр на талии дает меньшую прибавку к массе, чем на груди. А больше всего на вес влияет объем задницы. Впрочем, это знает любой интересующийся вопросом мужчина. То есть как минимум, наша модель реальной жизни не противоречит.

Валидация модели

Название громкое, но попробуем получить хотя бы ориентировочные веса тех девушек, для которых есть полный набор размеров, но нет веса. Их 7: с мая по июнь 1956 года, июль 1957, март 1987, август 1988. Находим предсказанные по модели веса: W_p=X*repr

Что ж, по крайней мере в текстовом виде выглядит правдоподобно. А насколько это соответствует реальности — решать вам

Применимость

Если вкратце — полученная модель годится для объектов, подобных нашему набору данных. То есть по полученным корреляциям не стоит считать параметры фигур женщин с весом 80+, возрастом, сильно отличающимся от среднего по больнице итд. В реальных применениях можно считать, что модель пригодна, если параметры изучаемого объекта не слишком отличаются от средних значений этих же параметров для исходного набора данных. Могут возникнуть (и возникнут) проблемы, если у нас предикторы сильно коррелированы между собой. То есть, например это рост и длина ног. Тогда коэффициенты для соответствующих величин в уравнении регрессии будут определены с малой точностью. В таком случае надо выбросить один из параметров, или воспользоваться методом главных компонент для снижения количества предикторов. Если у нас малая выборка и/или много предикторов, то мы рискуем попасть в переопределенность модели. То есть если мы возьмем 604 параметра для нашей выборки (а в таблице всего 604 девушки), то сможем аналитически получить уравнение с 604+1 слагаемым, которое абсолютно точно опишет то, что мы в него забросили. Но предсказательная сила у него будет весьма невелика. Наконец, далеко не все объекты можно описать мультилинейной зависимостью. Бывают и логарифмические, и степенные, и всякие сложные. Их поиск — это уже совсем другой вопрос.

Источник