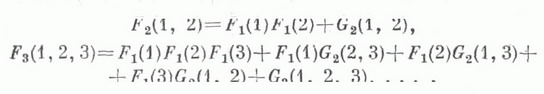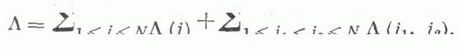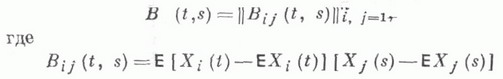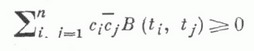что такое корреляционная функция

Корреляции для начинающих

Апдейт для тех, кто сочтет статью полезной и занесет в избранное. Есть приличный шанс, что пост уйдет в минуса, и я буду вынужден унести его в черновики. Сохраняйте копию!

Краткий и несложный материал для неспециалистов, рассказывающий в наглядной форме о различных методах поиска регрессионных зависимостей. Это все и близко не академично, зато надеюсь что понятно. Прокатит как мини-методичка по обработке данных для студентов естественнонаучных специальностей, которые математику знают плохо, впрочем как и автор. Расчеты в Матлабе, подготовка данных в Экселе — так уж повелось в нашей местности

Введение

Зачем это вообще надо? В науке и около нее очень часто возникает задача предсказания какого-то неизвестного параметра объекта исходя из известных параметров этого объекта (предикторов) и большого набора похожих объектов, так называемой учебной выборки. Пример. Вот мы выбираем на базаре яблоко. Его можно описать такими предикторами: красность, вес, количество червяков. Но как потребителей нас интересует вкус, измеренный в попугаях по пятибалльной шкале. Из жизненного опыта нам известно, что вкус с приличной точностью равен 5*красность+2*вес-7*количество червяков. Вот про поиск такого рода зависимостей мы и побеседуем. Чтобы обучение пошло легче, попробуем предсказать вес девушки исходя из ее 90/60/90 и роста.

Исходные данные

В качестве объекта исследования возьму данные о параметрах фигуры девушек месяца Плейбоя. Источник — www.wired.com/special_multimedia/2009/st_infoporn_1702, слегка облагородил и перевел из дюймов в сантиметры. Вспоминается анекдот про то, что 34 дюйма — это как два семнадцатидюймовых монитора. Также отделил записи с неполной информацией. При работе с реальными объектами их можно использовать, но сейчас они нам только мешают. Зато их можно использовать для проверки адекватности полученных результатов. Все данные у нас непрерывные, то есть грубо говоря типа float. Они приведены к целым числам только чтобы не загромождать экран. Есть способы работы и с дискретными данными — в нашем примере это например может быть цвет кожи или национальность, которые принимают одно из фиксированного набора значений. Это больше имеет отношение к методам классификации и принятия решений, что тянет еще на один мануал. Data.xls В файле два листа. На первом собственно данные, на втором — отсеянные неполные данные и набор для проверки нашей модели.

Обозначения

W — вес реальный
W_p — вес, предсказанный нашей моделью
S — бюст
T — талия
B — бедра
L — рост
E — ошибка модели

Как оценить качество модели?

Задача нашего упражнения — получить некую модель, которая описывает какой-либо объект. Способ получения и принцип работы конкретной модели нас пока не волнует. Это просто функция f(S, T, B, L), которая выдает вес девушки. Как понять, какая функция хорошая и качественная, а какая не очень? Для этого используется так называемая fitness function. Самая классическая и часто используемая — это сумма квадратов разницы предсказанного и реального значения. В нашем случае это будет сумма (W_p — W)^2 для всех точек. Собственно, отсюда и пошло название «метод наименьших квадратов». Критерий не лучший и не единственный, но вполне приемлемый как метод по умолчанию. Его особенность в том, что он чувствителен по отношению к выбросам и тем самым, считает такие модели менее качественными. Есть еще всякие методы наименьших модулей итд, но сейчас нам это пока не надо.

Простая линейная регрессия

Самый простой случай. У нас одна переменная-предиктор и одна зависимая переменная. В нашем случае это может быть например рост и вес. Нам надо построить уравнение W_p = a*L+b, т.е. найти коэффициенты a и b. Если мы проведем этот расчет для каждого образца, то W_p будет максимально совпадать с W для того же образца. То есть у нас для каждой девушки будет такое уравнение:
W_p_i = a*L_i+b
E_i = (W_p-W)^2

Общая ошибка в таком случае составит sum(E_i). В результате, для оптимальных значений a и b sum(E_i) будет минимальным. Как же найти уравнение?

Матлаб

Графичек

Мда, негусто. Это график W_p(W). Формула на графике показывает связь W_p и W. В идеале там будет W_p = W*1 + 0. Вылезла дискретизация исходных данных — облако точек клетчатое. Коэффициент корреляции ни в дугу — данные слабо коррелированы между собой, т.е. наша модель плохо описывает связь веса и роста. По графику это видно как точки, расположенные в форме слабо вытянутого вдоль прямой облака. Хорошая модель даст облако растянутое в узкую полосу, еще более плохая — просто хаотичный набор точек или круглое облако. Модель необходимо дополнить. Про коэффициент корреляции стоит рассказать отдельно, потому что его часто используют абсолютно неправильно.

Расчет в матричном виде

Мультилинейная регрессия

Попытка номер два

А так получше, но все равно не очень. Как видим, клетчатость осталась только по горизонтали. Никуда не денешься, исходные веса были целыми числами в фунтах. То есть после конверсии в килограммы они ложатся на сетку с шагом около 0.5. Итого финальный вид нашей модели:

W_p = 0.2271*S + 0.1851*T + 0.3125*B + 0.3949*L — 72.9132

Объемы в сантиметрах, вес в кг. Поскольку у нас все величины кроме роста в одних единицах измерения и примерно одного порядка по величине (кроме талии), то мы можем оценить их вклады в общий вес. Рассуждения примерно в таком духе: коэффициент при талии самый маленький, равно как и сами величины в сантиметрах. Значит, вклад этого параметра в вес минимален. У бюста и особенно у бедер он больше, т.е. сантиметр на талии дает меньшую прибавку к массе, чем на груди. А больше всего на вес влияет объем задницы. Впрочем, это знает любой интересующийся вопросом мужчина. То есть как минимум, наша модель реальной жизни не противоречит.

Валидация модели

Название громкое, но попробуем получить хотя бы ориентировочные веса тех девушек, для которых есть полный набор размеров, но нет веса. Их 7: с мая по июнь 1956 года, июль 1957, март 1987, август 1988. Находим предсказанные по модели веса: W_p=X*repr

Что ж, по крайней мере в текстовом виде выглядит правдоподобно. А насколько это соответствует реальности — решать вам

Применимость

Если вкратце — полученная модель годится для объектов, подобных нашему набору данных. То есть по полученным корреляциям не стоит считать параметры фигур женщин с весом 80+, возрастом, сильно отличающимся от среднего по больнице итд. В реальных применениях можно считать, что модель пригодна, если параметры изучаемого объекта не слишком отличаются от средних значений этих же параметров для исходного набора данных. Могут возникнуть (и возникнут) проблемы, если у нас предикторы сильно коррелированы между собой. То есть, например это рост и длина ног. Тогда коэффициенты для соответствующих величин в уравнении регрессии будут определены с малой точностью. В таком случае надо выбросить один из параметров, или воспользоваться методом главных компонент для снижения количества предикторов. Если у нас малая выборка и/или много предикторов, то мы рискуем попасть в переопределенность модели. То есть если мы возьмем 604 параметра для нашей выборки (а в таблице всего 604 девушки), то сможем аналитически получить уравнение с 604+1 слагаемым, которое абсолютно точно опишет то, что мы в него забросили. Но предсказательная сила у него будет весьма невелика. Наконец, далеко не все объекты можно описать мультилинейной зависимостью. Бывают и логарифмические, и степенные, и всякие сложные. Их поиск — это уже совсем другой вопрос.

Источник

КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ

Закон изменения D t во времени характеризуется уравнением Лиувилля в к-ром L представляет не зависящий явно от времени оператор Лиуйилля. Обычно рассматривается случай, когда L состоит из суммы аддитивной части и бинарной части, характеризующей взаимодействия между частицами:

Согласно принципу ослабления корреляции К. ф. удовлетворяют граничным условиям при max

К. ф. являются функциональными производными функционала

A t (и), связанного с так наз. производящим функционалом

Функционал A t (u)удовлетворяет уравнению

В квантовой статистич. механике К. ф. являются операторными величинами и определяются соотношениями;

Лит.:[1] Б о г о л ю б о в Н. Н., Проблемы динамической теории в статистической физике, М.- Л., 1946; 12] Б о г о л ю б о в Н. Н., Г у р о в К. П., «Ж. экспериментальной и теоретич. физики», 1947, т. 17, в. 7, с. 614-28; [3] Боголюбов Н. Н., Избранные труды, т. 3, К., 1971; [4] Боголюбов Н. Н., (м л.), Садовников Б. И., Некоторые вопросы статистической механики, М., 1975; [5] Б о г о л ю б о в Н. Н., Т я б л и к о в С. В., «Докл. АН СССР», 1959, т. 126, № 1, с. 53-56; [6] Л и б о в Р., Введение в теорию кинетических уравнений, пер. с англ., М., 1974; [7] И с и х а р а А., Статистическая физика, пер. с англ., М., 1973; [8] Р ю э л ь Д., Статистическая механика. Строгие результаты, пер. с англ., М., 1971; [9] П р е с т о н К. Дж., Гиббсовские состояния на счетных множествах, пер. с англ., М., 1977.

А. Н. Ермилов, А. М. Курбатов.

Полезное

Смотреть что такое «КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ» в других словарях:

корреляционная функция — Ндп. автокорреляционная функция Функция, равная среднему значению произведения переменной составляющей случайного сигнала и такой же переменной составляющей, но запаздывающей на заданное время. Примечание Корреляционная функция характеризует… … Справочник технического переводчика

КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ — в статистической физике ф ция, определяющая вероятность относит. расположения комплекса из s любых молекул жидкости или газа; при s=2 К. ф. наз. парной или бинарной. Появление корреляций в расположении молекул среды связано с тем, что в ближайшем … Физическая энциклопедия

Корреляционная функция — 24. Корреляционная функция Ндп. Автокорреляционная функция Функция, равная среднему значению произведения переменной составляющей случайного сигнала и такой же переменной составляющей, но запаздывающей на заданное время. Примечание.… … Словарь-справочник терминов нормативно-технической документации

Корреляционная функция — 1. Функция, равная среднему значению произведения переменной составляющей случайного сигнала и такой же переменной составляющей, но запаздывающей на заданное время Употребляется в документе: ГОСТ 16465 70 Сигналы радиотехнические измерительные.… … Телекоммуникационный словарь

КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ СЛУЧАЙНОГО ПРОЦЕССА — см. Функция корреляционная случайного процесса. Геологический словарь: в 2 х томах. М.: Недра. Под редакцией К. Н. Паффенгольца и др.. 1978 … Геологическая энциклопедия

Корреляционная функция случайного процесса — 16. Корреляционная функция случайного процесса Функция двух переменных t и и, равная ковариационной функции центрированного случайного процесса Rξ (t, u) = M<[ξ(t) m1]×[ξ(u) m2]>, t,uЄT Источник … Словарь-справочник терминов нормативно-технической документации

Нормированная корреляционная функция — 25. Нормированная корреляционная функция Ндп. Коэффициент корреляции Функция, равная отношению корреляционной функции случайного сигнала к его дисперсии Источник: ГОСТ 16465 70: Сигналы радиотехнические измерительные. Термины и определения … Словарь-справочник терминов нормативно-технической документации

Источник

Корреляционная функция

Корреляционная функция — функция времени или пространственных координат, которая задает корреляцию в системах со случайными процессами.

Зависящая от времени корреляция двух случайных функций X(t) и Y(t) определяется как:

,

где угловые скобки обозначают процедуру усреднения.

Если корреляционная функция вычисляется для одного и того же процесса, она называется автокорреляционной:

.

Аналогично можно вычислить корреляционную функцию для процессов, происходящих в разных точках пространства в различные моменты времени:

.

Корреляционные функции широко используются в статистической физике и других дисциплинах, изучающих случайные (стохастические) процессы.

Полезное

Смотреть что такое «Корреляционная функция» в других словарях:

корреляционная функция — Ндп. автокорреляционная функция Функция, равная среднему значению произведения переменной составляющей случайного сигнала и такой же переменной составляющей, но запаздывающей на заданное время. Примечание Корреляционная функция характеризует… … Справочник технического переводчика

КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ — в статистической физике ф ция, определяющая вероятность относит. расположения комплекса из s любых молекул жидкости или газа; при s=2 К. ф. наз. парной или бинарной. Появление корреляций в расположении молекул среды связано с тем, что в ближайшем … Физическая энциклопедия

Корреляционная функция — 24. Корреляционная функция Ндп. Автокорреляционная функция Функция, равная среднему значению произведения переменной составляющей случайного сигнала и такой же переменной составляющей, но запаздывающей на заданное время. Примечание.… … Словарь-справочник терминов нормативно-технической документации

Корреляционная функция — 1. Функция, равная среднему значению произведения переменной составляющей случайного сигнала и такой же переменной составляющей, но запаздывающей на заданное время Употребляется в документе: ГОСТ 16465 70 Сигналы радиотехнические измерительные.… … Телекоммуникационный словарь

КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ СЛУЧАЙНОГО ПРОЦЕССА — см. Функция корреляционная случайного процесса. Геологический словарь: в 2 х томах. М.: Недра. Под редакцией К. Н. Паффенгольца и др.. 1978 … Геологическая энциклопедия

Корреляционная функция случайного процесса — 16. Корреляционная функция случайного процесса Функция двух переменных t и и, равная ковариационной функции центрированного случайного процесса Rξ (t, u) = M<[ξ(t) m1]×[ξ(u) m2]>, t,uЄT Источник … Словарь-справочник терминов нормативно-технической документации

Нормированная корреляционная функция — 25. Нормированная корреляционная функция Ндп. Коэффициент корреляции Функция, равная отношению корреляционной функции случайного сигнала к его дисперсии Источник: ГОСТ 16465 70: Сигналы радиотехнические измерительные. Термины и определения … Словарь-справочник терминов нормативно-технической документации

Источник

КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ

действительного случайного процесса — функция аргументов t,. определяемая равенством

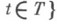
— взаимная корреляционная функция процессов X i (t), X j (t).

Скорость и характер убывания корреляций при 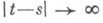дают представление об эргодических свойствах процесса. Условия на скорость убывания корреляций в той или иной форме присутствуют в предельных теоремах для случайных процессов. Локальные свойства 2-го порядка, такие как среднеквадратичные непрерывность, дифференцируемость, дают полезную, хотя и весьма грубую характеристику локального поведения процесса. Исследование свойств траекторий в терминах К. ф. с большой полнотой проведено в гауссовском случае (см. Выборочная функция). Одним из наиболее завершенных разделов теории случайных процессов является теория линейной экстраполяции и фильтрации, позволяющая находить оптимальные линейные алгоритмы прогноза и аппроксимации случайных процессов, основываясь на знании К. ф.

Характеристическим свойством К. ф. является положительная определенность:

Если R(t).дополнительно непрерывна при t= 0 (что соответствует среднеквадратичной непрерывности процесса X(t)), то

Лит.:[1] Дуб Дж., Вероятностные процессы, пер. с англ., М., 1956; [2] Л о э в М., Теория вероятностей, пер. с англ., М., 1962; [3] Г и х м а н И. И., Скороход А. В., Введение в теорию случайных процессов, М., 1965. А. С. Холево.

Источник

Корреляционная функция

Корреляционная функция — функция времени и пространственных координат, которая задает корреляцию в системах со случайными процессами.

Определение

Зависящая от времени корреляция двух случайных функций X ( t ) и Y ( t ) определяется как:

где угловые скобки обозначают процедуру усреднения.

Если корреляционная функция вычисляется для одного и того же процесса, она называется автокорреляционной:

Аналогично можно вычислить корреляционную функцию для процессов, происходящих в разных точках пространства в различные моменты времени:

Корреляционные функции широко используются в статистической физике и других дисциплинах, изучающих случайные (стохастические) процессы.

Корреляционная функция в статфизике

В статистической физике корреляционная функция описывает, как микроскопические переменные (например, скорости движения атомов) связаны в различных точках пространства в различные моменты времени. Наиболее общее определение имеет следующий вид:

Одновременные корреляционные функции

такая корреляционная функция называется одновременной.

Пространственные корреляционные функции

Иногда требуется рассмотреть временную эволюцию микроскопических переменных. Для этого используется пространственная корреляционная функция:

При этом важно понимать, что несмотря на то, что в равновесии некоторые макроскопические переменные не зависят от времени, микроскопические переменные (такие, как, например, вектор скорости частицы) могут зависеть от времени и поэтому подобные корреляционные функции, являющиеся по сути макроскопическими величинами, тоже могут зависеть от времени.

Примеры

Одним из примеров корреляционных функций может служить радиальная функция распределения.

Магнетизм

Еще одним классическим примером корреляционных функций может служить таковая в системе спинов, где она описывает их среднее по ансамблю скалярное произведение:

Даже в парамагнитной фазе спины скоррелированы, так как если расстояние между ними мало, то между спинами имеет место взаимодействие, которое и приводит к тому, что спины являются скоррелированными, однако их дальнейшему упорядочиванию препятствует тепловое движение. Поэтому оказывается, что корреляции между спинами экспоненциально уменьшаются с ростом расстояния между ними:

где r > — расстояние между спинами, d — размерность, η — т. н. критический индекс. При снижении температуры тепловое движение ослабевает, и радиус корреляции ξ cтремится к бесконечности:

где ν — другой критический индекс, T c > — температура Кюри.

Как следствие данной формулы, в таких системах возникает фазовый переход 2-го рода.

Корреляционная функция плотности числа частиц порядка s

В частности, в качестве примера можно рассмотреть корреляционную функцию плотности числа частиц порядка s — это функция вида

n ^ ( r ) = ∑ i = 1 N δ ( r − r i ) >left(mathbf ight)=sum limits _^delta (mathbf -mathbf _)>

называется микроскопической плотностью числа частиц в том смысле, что интегрируя ее по некому объему V, мы можем найти число частиц в нем:

∫ V n ^ ( r ) d r = N V >left(mathbf ight)mathrm mathbf =N_>

В случае s = 2 корреляционная функция плотности числа частиц называется парной.

Связная корреляционная функция плотности числа частиц

Имеет место т. н. принцип ослабления корреляций: многочастичные функции распределения классической системы распадаются на произведения многочастичных функций распределения с меньшим числом аргументов при безграничном увеличении разностей соответствующих аргументов, из которого, в частности, следует:

Следовательно, можно написать следующее выражение для двучастичной связной корреляционной функции плотности числа частиц:

Аналогично вводятся связные корреляционные функции плотности более высокого порядка числа частиц:

Производящий функционал

Для корреляционных функций плотности числа частиц может быть построен производящий функционал:

G ( a ) = ⟨ e ∫ a ( r ) n ^ ( r ) d r ⟩ ight)>left(mathbf ight)mathrm mathbf > ight angle >

Тогда корреляционная функция плотности вводится как вариационная производная от производящего функционала:

Аналогично может быть введена связная корреляционная функция:

Физический смысл

Корреляционная функция является мерой упорядоченности системы. Она показывает, как микроскопические переменные коррелируют в различные моменты времени в различных точках в среднем.

Физический смысл корреляционной функции плотности числа частиц состоит в том, что она показывает плотность вероятности относительного расположения s частиц. Появление корреляций обусловлено наличием взаимодействия между частицами, за счет которого возникает ближний порядок.

Важно отметить, что имеет место следующее соотношение:

где δ n ^ ( r ) = n ^ ( r ) − ⟨ n ^ ( r ) ⟩ >left(mathbf ight)=>left(mathbf ight)-leftlangle >left(mathbf ight) ight angle > есть флуктуация плотности. Таким образом, связная корреляционная функция плотности числа частиц описывает флуктуации плотности вероятности относительного расположения частиц.

Помимо этого, корреляционные функции в самом общем виде могут использоваться для нахождения прочих флуктуаций, например, флуктуаций числа частиц и температуры.

Корреляционная функция в квантовой теории поля

где T — Оператор хронологического упорядочивания, S — лагранжиан.

Корреляционную функцию также часто называют просто коррелятором.

Корреляционная функция в физике высоких энергий

В физике высоких энергий корреляционная функция есть мера корреляции между некоторыми наблюдаемыми величинами. При изучении адрон-адронных столкновений (например, протон-протонных или ядерно-ядерных) широко используется анализ корреляций между различными наблюдаемыми величинами, например, между поперечными импульсами или множественностями вторичных частиц, рождающихся в результате столкновения.

При изучении подобных процессов принято пользоваться такими переменными, как быстрота или псевдобыстрота. Обычно рассматриваются два интервала (называемых окнами) в пространстве быстрот, расположенных по разные стороны от места столкновения встречных пучков частиц в ускорителе, поэтому возникающие при этом корреляции между наблюдаемыми величинами, которые есть функции быстроты (или псевдобыстроты) часто называют «корреляциями вперед-назад».

Для определенности рассмотрим так называемые «корреляции множественность-множественность» где множественность есть функция, задающая число частиц, имеющих быстроту, принадлежащую некоторому заданному интервалу. В таком случае корреляционная функция вводится как зависимость средней множественности в одном (обычно — правом) быстротном интервале от множественности в другом интервале. В случае линейной корреляционной функции имеем для нее следующее выражение:

⟨ n f ⟩ ⟨ n b ⟩ = a + b ⋅ n b angle >_ angle >=a+bcdot n_>

Данное предположение вполне согласуется с экспериментальными данными, полученными на различных ускорителях элементарных частиц, в том числе SPS и Fermilab.Величина b из формулы выше носит название коэффициента дальних корреляций. Как следствие формулы выше, можно получить следующую формулу для коэффициента корреляций:

Найденный таким образом коэффициент корреляций позволяет изучать физику явлений, происходящих при столкновениях адронов. В частности, отличие коэффициента корреляции от нуля может означать, что изучаемые величины (в данном случае — множественности в переднем и заднем окне) каким-то образом связаны, но при этом возникающие зависимости не обязательно имеют причинно-следственные связи.

Оценка корреляционных функций и ее особенности

Оценка необходимых для расчётов корреляционных функций входных воздействий САУ производится экспериментально путем наблюдения за их реализациями в течение длительного времени Т и с расчётом по следующей формуле: r x ( τ ) = 1 / T ∫ 0 T x ( t ) x ( t + τ ) d t ( au )=1/Tint limits _<0>^x(t)x(t+ au )dt>

Источник