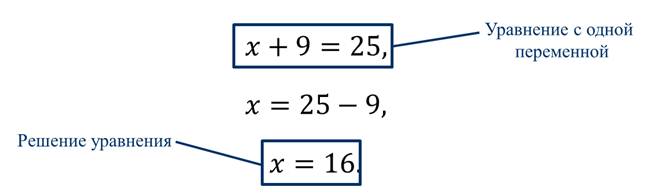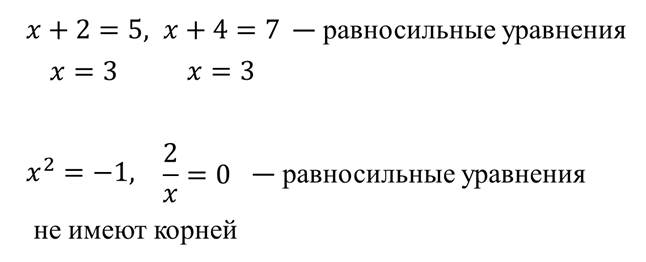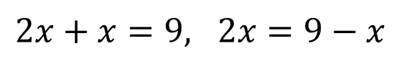что такое корни уравнения 7 класс

Уравнение и его корни: определения, примеры

После того, как мы изучили понятие равенств, а именно один из их видов – числовые равенства, можно перейти к еще одному важному виду – уравнениям. В рамках данного материала мы объясним, что такое уравнение и его корень, сформулируем основные определения и приведем различные примеры уравнений и нахождения их корней.

Понятие уравнения

Обычно понятие уравнения изучается в самом начале школьного курса алгебры. Тогда оно определяется так:

Уравнением называется равенство с неизвестным числом, которое нужно найти.

Далее, после того, как ученики знакомятся с понятием целых, действительных, рациональных, натуральных чисел, а также логарифмами, корнями и степенями, появляются новые уравнения, включающие в себя все эти объекты. Примерам таких выражений мы посвятили отдельную статью.

В программе за 7 класс впервые возникает понятие переменных. Это такие буквы, которые могут принимать разные значения (подробнее см. в статье о числовых, буквенных выражениях и выражениях с переменными). Основываясь на этом понятии, мы можем дать новое определение уравнению:

Уравнение – это равенство, включающее в себя переменную, значение которой нужно вычислить.

В одном уравнении может быть не одна переменная, а две и более. Их называют соответственно уравнениями с двумя, тремя переменными и др. Запишем определение:

Уравнениями с двумя (тремя, четырьмя и более) переменными называют уравнения, которые включают в себя соответствующее количество неизвестных.

Корень уравнения

Когда мы говорим об уравнении, сразу возникает необходимость определиться с понятием его корня. Попробуем объяснить, что оно означает.

Нас больше интересуют именно те значения, с которыми переменная обратится в верное равенство. Они и называются корнями или решениями. Запишем определение.

Корнем уравнения называют такое значение переменной, которое обращает данное уравнение в верное равенство.

Корень также можно назвать решением, или наоборот – оба эти понятия означают одно и то же.

Сколько корней может иметь одно уравнение? Любое ли уравнение имеет корень? Ответим на эти вопросы.

Также бывают уравнения, имеющие несколько корней. У них может быть как конечное, так и бесконечно большое количество корней.

Так, в уравнении x − 2 = 4 есть только один корень – шесть, в x 2 = 9 два корня ­­– три и минус три, в x · ( x − 1 ) · ( x − 2 ) = 0 три корня – нуль, один и два, в уравнении x=x корней бесконечно много.

Когда у уравнения два, три корня или больше, то, как правило, говорят не о корнях, а о решениях уравнения. Сформулируем определение решения уравнения с несколькими переменными.

Решение уравнения с двумя, тремя и более переменными – это два, три и более значения переменных, которые обращают данное уравнение в верное числовое равенство.

Поясним определение на примерах.

На практике чаще всего приходится иметь дело с уравнениями, содержащими одну переменную. Алгоритм их решения мы подробно рассмотрим в статье, посвященной решению уравнений.

Источник

Алгебра. 7 класс

Конспект урока

Решение линейных уравнений с одним неизвестным

Перечень рассматриваемых вопросов:

• Решение линейных уравнений.

Уравнение – это равенство, включающее в себя переменную, значение которой нужно вычислить.

Корень уравнения – это число, при подстановке которого в уравнение получается верное равенство.

Переменная – символ, используемый для представления величины, которая может принимать любое из ряда значений.

Свободный член – член уравнения, не содержащий неизвестного.

Решить уравнение – значит найти все его корни или установить, что их нет.

Преобразование – это действия, выполняемые с целью замены исходного выражения на выражение, которое будет тождественно равным исходному.

Основная литература:

1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.

1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.

2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.

3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения.

Давайте вспомним, что называется корнем уравнения?

Корнем уравнения называют, такое значение переменной, при которой уравнение преобразуется в верное числовое равенство.

А что же означает решить уравнение?

Решить уравнение означает найти все его корни или доказать, что корней нет.

Давайте попробуем сформулировать теперь, как решать линейные уравнения и подумаем, а какие у нас могут быть случаи?

Решение линейного уравнения – это приведение его путем тождественных преобразований к стандартному виду.

Давайте решим уравнение:

Следовательно, уравнение не имеет корней.

А теперь давайте решим другое уравнение:

Попробуем решить уравнение:

При любом значении переменной, уравнение принимает вид верного равенства:

0 = 0, следовательно, уравнение имеет бесконечное множество корней.

Отсюда можно сделать вывод, что возможные варианты решения уравнения, зависят от того, какие значения принимает свободный член и коэффициент при переменной.

При решении уравнения вида возможны следующие три случая:

Замечательно, а теперь узнаем, можно ли проверить, является число корнем уравнения не решая его?

Да, конечно можно. Для этого нужно подставить в уравнение вместо переменной это число, если после упрощения, мы получаем верное равенство, то данное число будет являться корнем уравнения.

Давайте проверим, так ли это. Узнаем, является ли число

Замечательно. А теперь давайте попробуем порешать линейные уравнения первой степени.

является корнем уравнения.

уравнение к стандартному виду. Слагаемые, зависящие от икс, перенесём в левую часть уравнения, числа – в правую, изменяя их знаки на противоположные.

Разбор заданий тренировочного модуля.

содержащие переменной в правую часть, меняя знак на противоположный;

слагаемые, содержащие переменную в левую часть, не содержащие переменной, в правую часть, меняя знак на противоположный;

Источник

Класс: 7

Презентация к уроку

Технические средства обучения: мультимедийный проектор.

Ход урока

1. Домашнее задание: п. 6, № 113, 117, 120.

Дети сдают диктанты, обмениваются тетрадями, проверяют друг у друга работы. Ответы проецируются на доску.

3. Сообщение темы урока.

— Каким было последнее задание в диктанте? (Решить уравнение).

— Учиться решать уравнения вы начали ещё в начальных классах. С этой темой мы встречались в 5 и 6 классах, узнавая каждый раз что – то новое об уравнениях. Задачей нашего сегодняшнего урока является обобщение и систематизация знаний об уравнениях.

4. Изучение нового материала (с применением компьютерной презентации).

1) – Запишите тему нашего урока “Уравнение и его корни”. (Слайд 1)

2) – Давайте постараемся дать определение уравнению. Что же это такое? (Слайд 2)

Равенство, содержащее переменную, называется уравнением с одной переменной или уравнением с одним неизвестным.

3) Помня определение уравнения, определите, является ли данная запись уравнением:

д) 1.5 х + 2.8 = 5,8. (Слайд 3)

Дети объясняют свои ответы, подчёркивая, является ли данная запись равенством и содержит ли она переменную.

Корнем уравнения называется значение переменной, при котором уравнение обращается в верное равенство.

— Проверим ваши ответы. (Слайд 4)

5) – Как узнать, является ли данное число корнем уравнения или нет? (Надо подставить число в уравнение вместо переменной, посмотреть, обратится ли при этом уравнение в верное равенство или нет.)

Выясните, является ли число 2 корнем уравнения:

в) 6(3х – 1) = 12х + 6. (Слайд 5)

Учащиеся подставляют число 2 в каждое уравнение, проверяя, обращает ли оно данное уравнение в верное равенство. Делают соответствующий вывод.

6) – Следующее задание выполним письменно.

Задание выполняется учащимися в тетради. Некоторые ученики по очереди делают соответствующие записи на доске.

Образец выполнения задания:

Корнем уравнения х 2 + 3х = 10 число

в) 0 не является, так как 0 2 + 3 * 0 = 0, а 0 10;

г) 2 является, так как 2 2 + 3 * 2 = 4 + 6 = 10, а 10 = 10;

д) 3 не является, так как 3 2 + 3 * 3 = 9 + 9 = 18, а 18 10.

— А теперь немного отдохнём. Сядьте удобно.

1. Делаем вертикальные движения глазами вверх – вниз.

2. Горизонтальные движения глазами вправо – влево.

3. “Нарисуем глазами линию” (на плакате изображено несколько линий, дети “ведут” по ним глазами от точки до точки).

— Следующие упражнения выполняем стоя.

4. – Поднимаем сначала правое плечо вверх, потом левое, опускаем сначала правое плечо, потом левое. Так продолжаем поочерёдно.

6. “Стряхиваем воду с кистей рук”.

8) – Продолжим работать дальше.

Постарайтесь сами составить уравнение, корнем которого было бы число 3. (Слайд 7)

После самостоятельного выполнения задания некоторые учащиеся зачитывают получившиеся у них уравнения, класс определяет, правильно ли выполнено задание.

9) – Как вы думаете, что значит решить уравнение?

Решить уравнение – значит найти его корни или доказать, что корней нет. (Слайд 8)

10) – Какие из данных уравнений не имеют корней:

в) 3х + 12 = 3(х + 4). (Слайд 9)

Дети дают ответы, обосновывая их.

11) – Что называется модулем числа?

— Чему равен модуль положительного числа?

— Модуль нуля? Отрицательного числа?

— Может ли модуль числа равняться отрицательному числу?

Как вы думаете, имеют ли данные уравнения корни и, если имеют, то сколько:

г) l х l = 2,5. (Слайд 10)

12) – Сегодня мы знакомимся с новым для вас понятием – это равносильные уравнение. Попробуйте догадаться, какие же уравнения называются равносильными.

Уравнения, имеющие одни и те же корни, называются равносильными уравнениями. (Слайд 11)

13) – Какое уравнение равносильно уравнению 3х – 10 = 50? (Слайд 12)

Учащиеся составляют уравнения, равносильные данному, записывают их в тетрадь, некоторые из составленных уравнений зачитываются и обсуждаются классом.

14) – При решении уравнений используются свойства, которые мы с вами учили в 6 классе. Давайте их вспомним. (Слайд 13)

1) Если в уравнении перенести слагаемое из одной части в другую, изменив его знак на противоположный, то получится уравнение, равносильное данному.

2) Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.

15) – Замените уравнения равносильными уравнениями с целыми коэффициентами:

— Замените уравнения равносильными уравнениями вида ах = b:

б) 16 – 2х = 10. (Слайд 15)

5. Подведение итогов урока. (Слайд 16)

— Дайте определение уравнения с одной переменной.

— Что называют корнем уравнения?

— Все ли уравнения имеют корни?

— Что значит решить уравнение?

— Какие уравнения называются равносильными?

— Назовите свойства, которые используются при решении уравнений.

Использованная литература.

Учебник “Алгебра. 7 класс” под редакцией С. А. Теляковского, Москва “Просвещение”, 2009 год.

Источник

Уравнение и его корни

Урок 7. Алгебра 7 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Уравнение и его корни»

· ввести понятия «уравнение с одной переменной», «решение уравнений с одной переменной»;

· разобрать что значит «решить уравнение»;

· ввести понятие равносильных уравнений.

Рассмотрим следующую задачу.

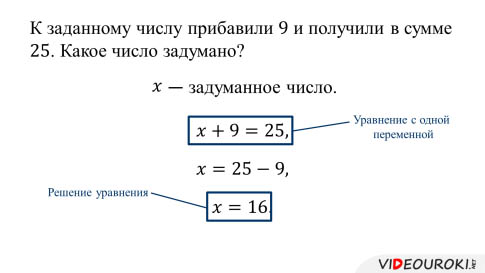
К заданному числу прибавили 9 и получили в сумме 25. Какое число задумано?

Обозначим букой х задуманное число. Тогда по условию задачи

То есть, чтобы найти неизвестное число, мы составили равенство, которое содержит переменную х. Равенства такого вида называются уравнениями с одной переменной.

Теперь надо найти такое значение переменной х, при подстановке которого в наше уравнение получается верное числовое равенство. Для этого переносим 9 в правую часть равенства и получаем:

То есть 16 и есть задуманное число.

Найденное значение переменной х называется решением уравнения, или корнем уравнения.

Таким образом, можем сформулировать следующие определения.

Равенство, содержащее одну переменную, называется уравнением с одной переменной, или уравнением с одним неизвестным.

Значение переменной, при котором уравнение превращается в верное числовое равенство, называется корнем (или решением) уравнения.

Рассмотренное выше уравнение имеет один корень.

Но есть уравнения, которые имеют два, три, четыре и более корней или не имеют корней вообще.

Решить уравнение – это значит найти все его корни или доказать, что их нет.

Два уравнения называются равносильными, если каждый корень первого уравнения является корнем второго, и наоборот – каждый корень второго уравнения является корнем первого, то есть, оба уравнения имеют одни и те же корни.

Равносильными являются также уравнения, которые не имеют корней.

А теперь сформулируем свойства, которые используются при решении уравнений.

Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному.

Также, если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнения, равносильное исходному.

Источник

Что такое уравнение и корни уравнения? Как решить уравнение?

Уравнения бывают разные. Вы изучите их многие виды в курсе математике, но все они решаются по одним правилам, эти правила мы сейчас рассмотрим подробно.

Что такое уравнение? Смысл и понятия.

Узнаем сначала все понятия, связанные с уравнением.

Определение:
Уравнение – это равенство, содержащее переменные и числовые значения.

Переменные (аргументы уравнения) или неизвестные уравнения – их обозначают в основном латинскими буквами (x, y, z, f и т.д.). При подстановки числового значения переменной в уравнение получаем верное равенство – это корень уравнения.

Решить уравнение – это значит найти все корни уравнения или доказать, что у данного уравнения нет корней.

Корни уравнения – это значение переменной при котором уравнение превращается в верное равенство.

Рассмотрим теперь, все термины на простом примере:
x+1=3

В данном случае x – переменная или неизвестное значение уравнения.

Можно устно решить данное уравнение. Какое надо число прибавить к 1, чтобы получить 3? Конечно, число 2. То есть наша переменная x =2. Корень уравнения равен 2. Проверим правильно ли мы решили уравнение? Чтобы проверить уравнение, нужно вместо переменной подставить полученный корень уравнения.

Получили верное равенство. Значит, правильно нашли корни уравнения.

Но бывают более сложные уравнения, которые устно не решить. Нужно прибегать к правилам решения уравнений. Рассмотрим правила решения уравнений ниже, которые объяснят нам как решать уравнения.

Правила уменьшения или увеличения уравнения на определенное число.

Чтобы понять правило рассмотрим подробно простой пример:
Решите уравнение x+2=7

Решение:
Чтобы решить данное уравнение нужно левую и правую часть уменьшить на 2. Это нужно сделать для того, чтобы переменная x осталась слева, а известные (т.е. числа) справа. Что значит уменьшить на 2? Это значит отнять от левой части двойку и одновременно от правой части отнять двойку. Если мы делаем какое-то действие, например, вычитание применяя его одновременно к левой части уравнения и к правой, то уравнение не меняет смысл.

Как проверить правильно ли вы нашли корень уравнения? Ведь не все уравнения будут простыми как данное. Чтобы проверить корень уравнения его значение нужно поставить в само уравнение.

Проверка:
Вместо переменной x подставим 5.

x+2=7
5+2=7
Получили верное равенство, значит уравнение решено верно.
Ответ: 5.

Разберем следующий пример:
Решите уравнение x-4=12.

Решение:
Чтобы решить данное уравнение нужно увеличить левую и правую часть уравнения на 4, чтобы переменная x осталось в левой стороне, а известные (т.е. числа) в правой стороне. Прибавим к левой и правой части число 4. Получим:

Теперь выполним проверку, вместо переменной x подставим в уравнение полученное число 16.
x-4=12
16-4=12
Ответ: 16

Очень важно понять правила переноса частей уравнения через знак равно. Не всегда нужно переносить числа, иногда нужно перенести переменные или даже целые выражения.

Рассмотрим пример:
Решите уравнение 4+3x=2x-5

Теперь, когда все неизвестные в левой стороне, а все известные в правой стороне посчитаем их.
(3-2)x=-9
1x=-9 или x=-9

Получилось верное равенство, уравнение решено верно.
Ответ: корень уравнения x=-9.

Правила уменьшения или увеличения уравнения в несколько раз.

Данное правило подходит тогда, когда вы уже посчитали все неизвестные и известные, но какой-то коэффициент остался перед переменной. Чтобы избавится от не нужного коэффициента мы применяем правило уменьшения или увеличения в несколько раз коэффициент уравнения.

Рассмотрим пример:
Решите уравнение 5x=20.

Решение:
В данном уравнение не нужно переносить переменные и числа, все компоненты уравнения стоят на месте. Но нам мешает коэффициент 5 который стоит перед переменной x. Мы не можем его просто взять и перенести в правую сторону уравнения, потому что между число 5 и переменно x стоит умножение 5⋅х. Если бы между переменной и числом стоял знак плюс или минус, мы могли бы 5 перенести вправо. Но мы так поступить не можем. За то мы можем все уравнение уменьшить в 5 раз или поделить на 5. Обязательно делим правую и левую сторону одновременно.

5x=20
5x :5 =20 :5
5:5x=4
1x=4 или x=4

Делаем проверку уравнения. Вместо переменной x подставляем 4.
5x=20
5⋅ 4 =20
20=20 получили верное равенство, корень уравнение найден правильно.
Ответ: x=4.

Решение:
Так как перед переменной x стоит коэффициент необходимо от него избавиться. Надо все уравнение увеличить в 3 раза или умножить на 3, обязательно умножаем левую часть уравнения и правую часть.

Сделаем проверку уравнения. Подставим вместо переменной x полученный корень уравнения 21.

7=7 получено верное равенство.

Ответ: корень уравнения равен x=21.

Следующий пример:
Найдите корни уравнения

Далее делим все уравнение на 3.

Сделаем проверку. Подставим в уравнение найденный корень.

Как решать уравнения? Алгоритм действий.

Подведем итог разобранной теме уравнений, рассмотрим общие правила решения уравнений:

Эти правила действуют на любой вид уравнения (линейный, квадратный, логарифмический, тригонометрический, рациональные, иррациональные, показательные и другие виды). Поэтому важно понять эти простые правила и научиться ими пользоваться.

Источник