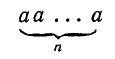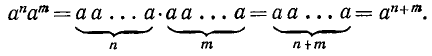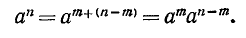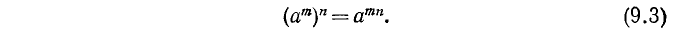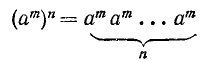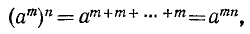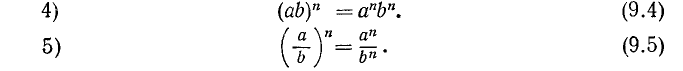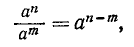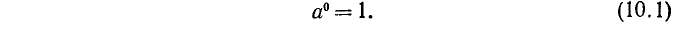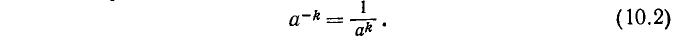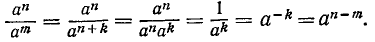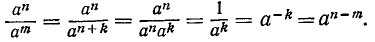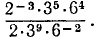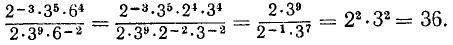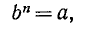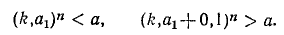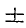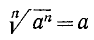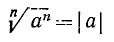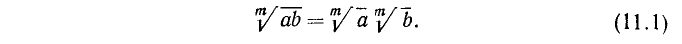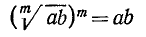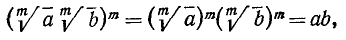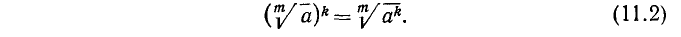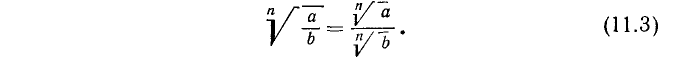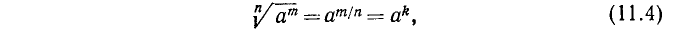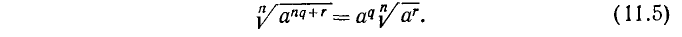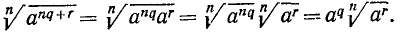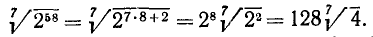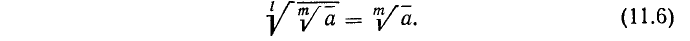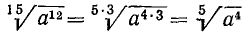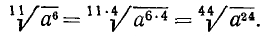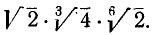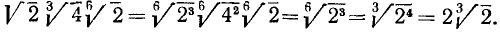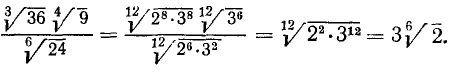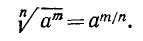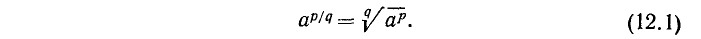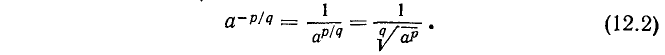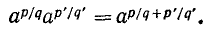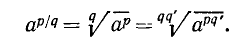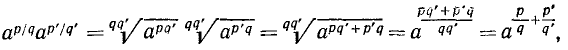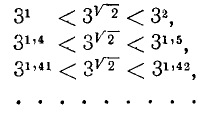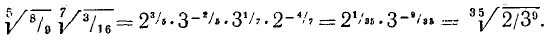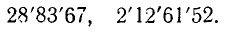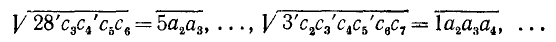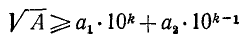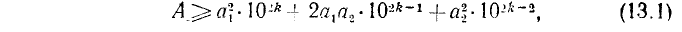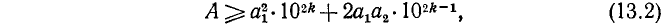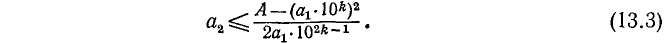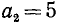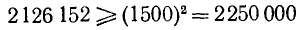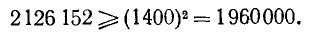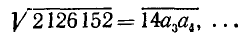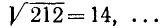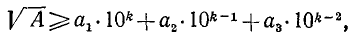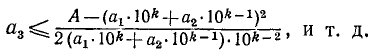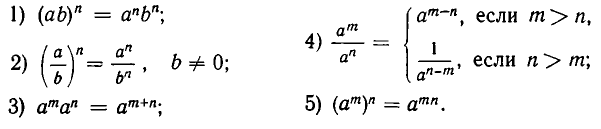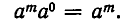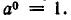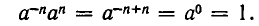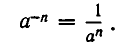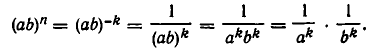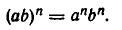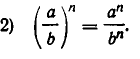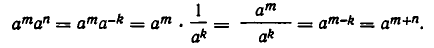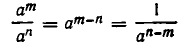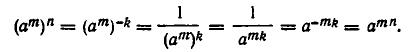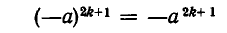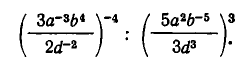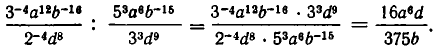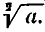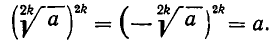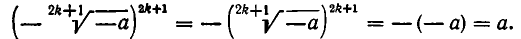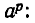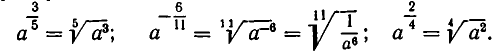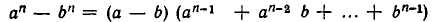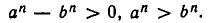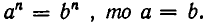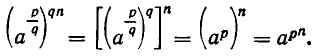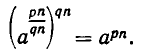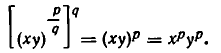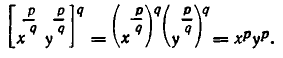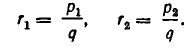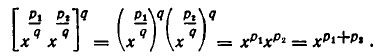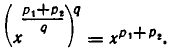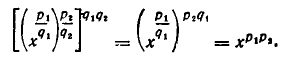что такое корни и степени определение
Корень n-ой степени
Определение корня n-й степени из действительного числа
Корнем n-й степени (\(n=2, 3, 4, 5, 6… \)) некоторого числа \(a\) называют такое неотрицательное число \(b\), которое при возведении в степень \(n\) дает \(a\):
Число \(n\) при этом называют показателем корня.
Если \(n=2\), то перед вами корень 2-й степени или обычный квадратный корень.
Если \(n=3\), то корень 3-й степени и т.д.
Операция извлечения корня n-й степени является обратной к операции возведения в n-ю степень.
Кубический корень из числа 27 равняется 3. Действительно, если число 3 возвести в 3-ю степень, то мы получим 27.
Корень 4-й степени из 16-и равен 2. Двойка в 4-й степени равна 16.
Если извлечь корень n-й степени из 0, всегда будет 0.
Мы не можем в уме подобрать такое число, которое при возведении в 3-ю степень даст 19. Если посчитать на калькуляторе, то получим \(2,668…\) – иррациональное число с бесконечным количеством знаков после запятой.
Обычно, в математике, когда у вас получается иррациональное число, корень не считают и оставляют так как есть \(\sqrt[3]<19>\).
Что же делать, если под рукой нет калькулятора, а нужно оценить, чему равен такой корень. В этом случае нужно подобрать справа и слева такие ближайшие числа, корень из которых посчитать можно:
Получается, что наш корень лежит между числами 2 и 3.
Корень четной и нечетной степени
Надо четко различать правила работы четными и нечетными степенями. Дело в том, что корень четной степени можно взять только из положительного числа. Из отрицательных чисел корень четной степени не существует.
Корень нечетной степени можно посчитать из любых действительных чисел. Иногда в школьной программе встречаются задания, в которых требуется определить имеет ли смысл выражение:
Данное выражение имеет смысл, так как корень нечетной степени можно посчитать из любого числа, даже отрицательного.
Так как корень четной степени, а под корнем стоит отрицательное число, то выражение не имеет смысла.
Свойства корня n-й степени
Пусть есть два неотрицательных числа a и b, для них будут выполняться следующие свойства:
Корни нужны для точных и сокращенных подсчетов в математике. Это необходимая функция, без которой представить современную математику невозможно. Корень n-ой степени обозначается при помощи всем известного значка радикала. Даже самый простой корень из двух будет равен длинному набору чисел, округлив который вы получите лишь приблизительное значение. Такие числа называются иррациональными и намного лучше представить их в виде радикала.
В данном учебном ролике в понятной форме изложены все основные свойства и теоремы корней n-ой степени. Тема непонятна для большинства школьников 7-9 классов, но не по причине их сложности (всего пара определений и свойств), а вследствие неправильной подачи информации в учебниках. Поэтому в данном видео мы расскажем о самом грамотном и понятном определении корня – все то, что действительно нужно запомнить. Далее покажем, как все это можно применить на практике.
Корень степени N: основные определения
Поздравляю: сегодня мы будем разбирать корни — одну из самых мозговыносящих тем 8-го класса.:)

Многие путаются в корнях не потому, что они сложные (чего там сложного-то — пара определений и ещё пара свойств), а потому что в большинстве школьных учебников корни определяются через такие дебри, что разобраться в этой писанине могут разве что сами авторы учебников. Да и то лишь с бутылкой хорошего виски.:)
Поэтому сейчас я дам самое правильное и самое грамотное определение корня — единственное, которое вам действительно следует запомнить. А уже затем объясню: зачем всё это нужно и как это применять на практике.
Но сначала запомните один важный момент, про который многие составители учебников почему-то «забывают»:
Вот в этом грёбаном «несколько отличается» скрыто, наверное, 95% всех ошибок и недопонимания, связанного с корнями. Поэтому давайте раз и навсегда разберёмся с терминологией:
В любом случае корень обозначается вот так:
Примеры. Классические примеры квадратных корней:
Кубические корни тоже часто встречаются — не надо их бояться:
Ну, и парочка «экзотических примеров»:
Если вы не поняли, в чём разница между чётной и нечётной степенью — перечитайте определение ещё раз. Это очень важно!
А мы тем временем рассмотрим одну неприятную особенность корней, из-за которой нам и потребовалось вводить раздельное определение для чётных и нечётных показателей.
Зачем вообще нужны корни?
Прочитав определение, многие ученики спросят: «Что курили математики, когда это придумывали?» И вправду: зачем вообще нужны все эти корни?
Чтобы ответить на этот вопрос, вернёмся на минутку в начальные классы. Вспомните: в те далёкие времена, когда деревья были зеленее, а пельмени вкуснее, основная наша забота была в том, чтобы правильно умножать числа. Ну, что-нибудь в духе «пять на пять — двадцать пять», вот это вот всё. Но ведь можно умножать числа не парами, а тройками, четвёрками и вообще целыми комплектами:
Ну и так далее. Ладно, ладно: последние две строчки я считал на калькуляторе.:)
Однако суть не в этом. Фишка в другом: математики — людишки ленивые, поэтому им было в лом записывать умножение десяти пятёрок вот так:
\[5\cdot 5\cdot 5\cdot 5\cdot 5\cdot 5=15\ 625\]
Поэтому они придумали степени. Почему бы вместо длинной строки не записать количество множителей в виде верхнего индекса? Типа вот такого:
\[5\cdot 5\cdot 5\cdot 5\cdot 5\cdot 5=<<5>^<6>>=15\ 625\]
Проблема эта оказалась гораздо более глобальной, чем может показаться на первый взгляд. Потому что выяснилось, что для большинства «готовых» степеней таких «исходных» чисел нет. Судите сами:
Не спорю: зачастую эти корни легко считаются — мы видели несколько таких примеров выше. Но всё-таки в большинстве случаев, если вы загадаете произвольное число, а затем попробуете извлечь из него корень произвольной степени, вас ждёт жестокий облом.
Как видите, после запятой идёт бесконечная последовательность цифр, которые не подчиняются никакой логике. Можно, конечно, округлить это число, чтобы быстро сравнить с другими числами. Например:
\[\sqrt<2>=1,4142. \approx 1,4 \lt 1,5\]
Или вот ещё пример:
\[\sqrt<3>=1,73205. \approx 1,7 \gt 1,5\]
Но все эти округления, во-первых, довольно грубые; а во-вторых, работать с примерными значениями тоже надо уметь, иначе можно словить кучу неочевидных ошибок (кстати, навык сравнения и округления в обязательном порядке проверяют на профильном ЕГЭ).
Рассмотрим несколько примеров, где после всех вычислений иррациональные числа всё же останутся в ответе.
Именно для этого их и придумали. Чтобы удобно записывать ответы.
Почему нужны два определения?
Внимательный читатель уже наверняка заметил, что все квадратные корни, приведённые в примерах, извлекаются из положительных чисел. Ну, в крайнем случае из нуля. А вот кубические корни невозмутимо извлекаются абсолютно из любого числа — хоть положительного, хоть отрицательного.
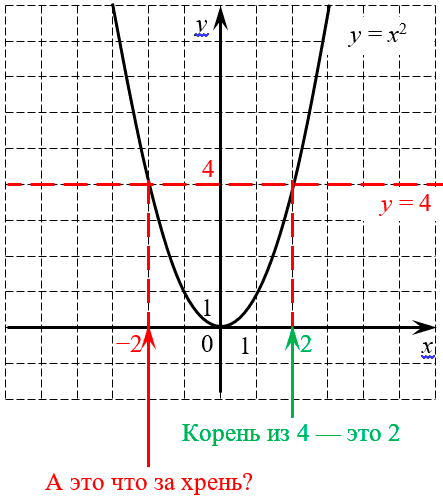
С первым числом всё понятно — оно положительное, поэтому оно и есть корень:
Но что тогда делать со второй точкой? Типа у четвёрки сразу два корня? Ведь если возвести в квадрат число −2, мы тоже получим 4. Почему бы тогда не записать$\sqrt<4>=-2$? И почему учителя смотрят на подобные записи так, как будто хотят вас сожрать?:)
В том-то и беда, что если не накладывать никаких дополнительных условий, то квадратных корней у четвёрки будет два — положительный и отрицательный. И у любого положительного числа их тоже будет два. А вот у отрицательных чисел корней вообще не будет — это видно всё по тому же графику, поскольку парабола нигде не опускается ниже оси y, т.е. не принимает отрицательных значений.
Подобная проблема возникает у всех корней с чётным показателем:
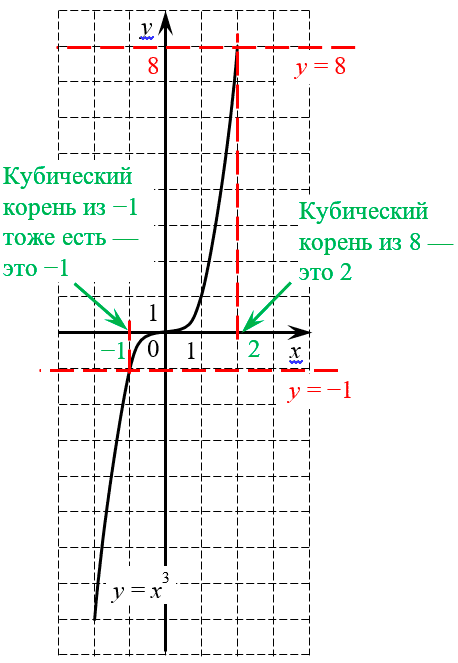
Из этого графика можно сделать два вывода:
Жаль, что эти простые вещи не объясняют в большинстве учебников. Вместо этого нам начинают парить мозг всякими арифметическими корнями и их свойствами.
Но сначала надо чётко усвоить то определение, которое я дал выше. Иначе из-за обилия терминов в голове начнётся такая каша, что в итоге вообще ничего не поймёте.
А всего-то и нужно понять разницу между чётными и нечётными показателями. Поэтому ещё раз соберём всё, что действительно нужно знать о корнях:
Разве это сложно? Нет, не сложно. Понятно? Да вообще очевидно! Поэтому сейчас мы немного потренируемся с вычислениями.
Основные свойства и ограничения
У корней много странных свойств и ограничений — об этом будет отдельный урок. Поэтому сейчас мы рассмотрим лишь самую важную «фишку», которая относится лишь к корням с чётным показателем. Запишем это свойство в виде формулы:
Чтобы детально разобраться в вопросе, давайте на минуту забудем все формулы и попробуем посчитать два числа напролом:
Это очень простые примеры. Первый пример решит большинство людишек, а вот на втором многие залипают. Чтобы без проблем решить любую подобную хрень, всегда учитывайте порядок действий:
Затем извлекаем корень четвёртой степени из числа 81:
Теперь сделаем то же самое со вторым выражением. Сначала возводим число −3 в четвёртую степени, для чего потребуется умножить его само на себя 4 раза:
Получили положительное число, поскольку общее количество минусов в произведении — 4 штуки, и они все взаимно уничтожится (ведь минус на минус даёт плюс). Дальше вновь извлекаем корень:
В принципе, эту строчку можно было не писать, поскольку и ежу понятно, что ответ получится один и тот же. Т.е. чётный корень из той же чётной степени «сжигает» минусы, и в этом смысле результат неотличим от обычного модуля:
Эти вычисления хорошо согласуются с определением корня чётной степени: результат всегда неотрицателен, да и под знаком радикала тоже всегда стоит неотрицательное число. В противном случае корень не определён.
Замечание по поводу порядка действий
Таким образом, ни в коем случае нельзя бездумно сокращать корни и степени, тем самым якобы «упрощая» исходное выражение. Потому что если под корнем стоит отрицательное число, а его показатель является чётным, мы получим кучу проблем.
Впрочем, все эти проблемы актуальны лишь для чётных показателей.
Вынесение минуса из-под знака корня
Естественно, у корней с нечётными показателями тоже есть своя фишка, которой в принципе не бывает у чётных. А именно:
Короче говоря, можно выносить минус из-под знака корней нечётной степени. Это очень полезное свойство, которое позволяет «вышвырнуть» все минусы наружу:
Это простое свойство значительно упрощает многие вычисления. Теперь не нужно переживать: вдруг под корнем затесалось отрицательное выражение, а степень у корня оказалась чётной? Достаточно лишь «вышвырнуть» все минусы за пределы корней, после чего их можно будет умножать друг на друга, делить и вообще делать многие подозрительные вещи, которые в случае с «классическими» корнями гарантированно приведут нас к ошибке.
И вот тут на сцену выходит ещё одно определение — то самое, с которого в большинстве школ и начинают изучение иррациональных выражений. И без которого наши рассуждения были бы неполными. Встречайте!
Арифметический корень
Давайте предположим на минутку, что под знаком корня могут находиться лишь положительные числа или в крайнем случае ноль. Забьём на чётные/нечётные показатели, забьём на все определения, приведённые выше — будем работать только с неотрицательными числами. Что тогда?
А тогда мы получим арифметический корень — он частично пересекается с нашими «стандартными» определениями, но всё же отличается от них.
Как видим, нас больше не интересует чётность. Взамен неё появилось новое ограничение: подкоренное выражение теперь всегда неотрицательно, да и сам корень тоже неотрицателен.
Чтобы лучше понять, чем арифметический корень отличается от обычного, взгляните на уже знакомые нам графики квадратной и кубической параболы:
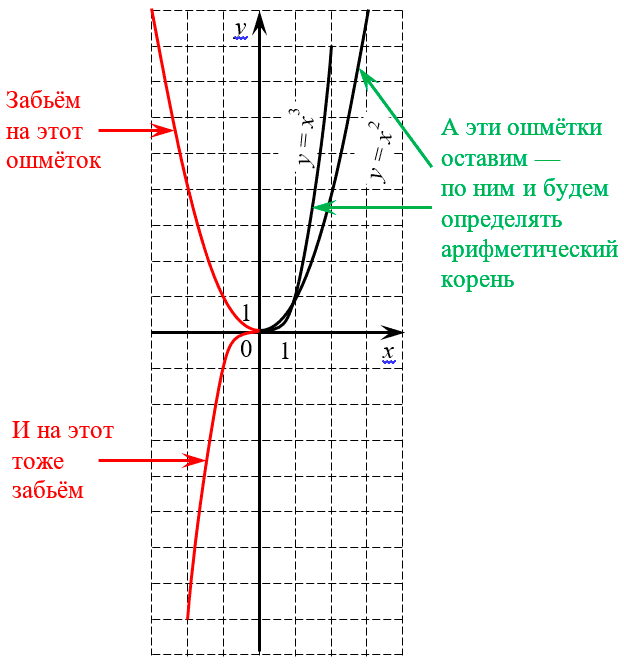
Возможно, вы спросите: «Ну и зачем нам такое кастрированное определение?» Или: «Почему нельзя обойтись стандартным определением, данным выше?»
Что ж, приведу всего одно свойство, из-за которого новое определение становится целесообразным. Например, правило возведения в степень:
Обратите внимание: мы можем возвести подкоренное выражение в любую степень и одновременно умножить на эту же степень показатель корня — и в результате получится то же самое число! Вот примеры:
Как видите, в первом случае мы вынесли минус из-под радикала (имеем полное право, т.к. показатель нечётный), а во втором — воспользовались указанной выше формулой. Т.е. с точки зрения математики всё сделано по правилам.
WTF?! Как одно и то же число может быть и положительным, и отрицательным? Никак. Просто формула возведения в степень, которая прекрасно работает для положительных чисел и нуля, начинает выдавать полную ересь в случае с отрицательными числами.
Вот для того, чтобы избавиться от подобной неоднозначности, и придумали арифметические корни. Им посвящён отдельный большой урок, где мы подробно рассматриваем все их свойства. Так что сейчас не будем на них останавливаться — урок и так получился слишком затянутым.
Алгебраический корень: для тех, кто хочет знать больше
Долго думал: выносить эту тему в отдельный параграф или нет. В итоге решил оставить здесь. Данный материал предназначен для тех, кто хочет понять корни ещё лучше — уже не на среднем «школьном» уровне, а на приближенном к олимпиадному.
Принципиальное отличие от стандартного определения, приведённого в начале урока, состоит в том, что алгебраический корень — это не конкретное число, а множество. А поскольку мы работаем с действительными числами, это множество бывает лишь трёх типов:
Последний случай заслуживает более подробного рассмотрения. Посчитаем парочку примеров, чтобы понять разницу.
Решение. С первым выражением всё просто:
Именно два числа входят в состав множества. Потому что каждое из них в квадрате даёт четвёрку.
Тут мы видим множество, состоящее лишь из одного числа. Это вполне логично, поскольку показатель корня — нечётный.
Наконец, последнее выражение:
Получили пустое множество. Потому что нет ни одного действительного числа, которое при возведении в четвёртую (т.е. чётную!) степень даст нам отрицательное число −16.
Однако в современном школьном курсе математики комплексные числа почти не встречаются. Их вычеркнули из большинства учебников, поскольку наши чиновники считают эту тему «слишком сложной для понимания».
На этом всё. В следующем уроке мы рассмотрим все ключевые свойства корней и научимся, наконец, упрощать иррациональные выражения.:)
Свойства корней (ОГЭ, ЕГЭ 2022)
А сейчас мы рассмотрим свойства корней.
Квадратный корень, кубический корень и корень в N-ой степени.
Порешаем задачки, чтобы к концу этого занятия все, что касается корней (в любой степени) было тебе абсолютно понятно!
И, самое главное, чтобы ты смог решить любую задачу c корнями на экзамене!Поехали!
Свойства корней — коротко о главном
Квадратным корнем (арифметическим квадратным корнем) из неотрицательного числа \( a\) называется такое неотрицательное число, квадрат которого равен \( a\)
Свойства корней:
Для любого натурального \( n\), целого \( k\) и любых неотрицательных чисел \( a\) и \( b\) выполнены равенства:
Арифметический квадратный корень
Когда ты разберешься в этой теме, тебе станет намного легче решать иррациональные уравнения и неравенства.
А пока что давай попробуем разобраться, что это за понятие «корень» и с чем его едят 🙂
Для этого рассмотрим примеры, с которыми ты уже сталкивался на уроках (ну, или тебе с этим только предстоит столкнуться).
К примеру, перед нами уравнение \( <
Для упрощения, математики ввели специальное понятие квадратного корня и присвоили ему специальный символ \( \sqrt<\ \ >\).
Дадим определение арифметическому квадратному корню.
Квадратным корнем (арифметическим квадратным корнем) из неотрицательного числа \( a\) называется такое неотрицательное число, квадрат которого равен \( a\)
\( \left( \sqrt=x,\ <^<2>>=a;\ \ x,a\ge 0 \right)\)
А почему же число \( a\) должно быть обязательно неотрицательным?
Например, чему равен \( \sqrt<-9>\). Так-так, попробуем подобрать. Может, три?
Это надо запомнить: число или выражение под знаком корня должно быть неотрицательным!
Однако самые внимательные уже наверняка заметили, что в определении сказано, что решение квадратного корня из «числа \( a\) называется такое неотрицательное число, квадрат которого равен \( a\)».
Такое замечание вполне уместно. Здесь необходимо просто разграничить понятия квадратных уравнений и арифметического квадратного корня из числа.
Квадратное уравнение или квадратный корень?
К примеру, \( <
Из \( <
А из \( x=\sqrt<4>\) следует, что \( x=2\).
Конечно, это очень путает, но это необходимо запомнить, что знаки являются результатом решения уравнения, так как при решении уравнения мы должны записать все иксы, которые при подстановке в исходное уравнение дадут верный результат.
Однако, если просто извлекать квадратный корень из чего-либо, то всегда получаем один неотрицательный результат.
А теперь попробуй решить такое уравнение \( <
Уже все не так просто и гладко, правда? Попробуй перебрать числа, может, что-то и выгорит?
Начнем с самого начала – с нуля: \( <<0>^<2>>=0\) – не подходит.
Двигаемся дальше \( \text
А что если \( x=2\); \( <<2>^<2>>=4\) – тоже не подходит, т.к. это больше трех.
С отрицательными числами получится такая же история.
И что же теперь делать? Неужели перебор нам ничего не дал?
Кроме того, очевидно, что решения не будут целыми числами. Более того, они не являются рациональными. И что дальше?
Давай построим график функции \( y=<
Давай попробуем обмануть систему и получить ответ с помощью калькулятора! Извлечем корень из \( 3\), делов-то! Ой-ой-ой, выходит, что \( \sqrt<3>=1,732050807568…\).
Такое число никогда не кончается.
Такие числа называются иррациональными, именно для упрощения записи таких чисел и было введено понятие квадратного корня.
Рассмотрим еще один пример для закрепления.
Разберем такую задачку: тебе необходимо пересечь по диагонали квадратное поле со стороной \( \displaystyle 1\) км, сколько км тебе предстоит пройти?
Самое очевидное здесь рассмотреть отдельно треугольник и воспользоваться теоремой Пифагора: \( <
Так чему же здесь равно искомое расстояние?
Чтобы решение примеров с корнями не вызывало проблем, необходимо их видеть и узнавать. Для этого необходимо знать, по меньшей мере, квадраты чисел от \( 1\) до \( 20\), а также уметь их распознать.
К примеру, необходимо знать, что \( 15\) в квадрате равно \( 225\), а также, наоборот, что \( 225\) – это \( 15\) в квадрате.
Вот тебе полная таблица квадратов чисел. Сверху строка — основание степени, слева в столбик показатель степени, на пересечение искомое значение степени. Запомнить нужно только то, что выделено зеленым.
Уловил, что такое квадратный корень? Тогда порешай несколько примеров.
Корни и степени
Здесь — основание степени, — показатель степени.
Степень с натуральным показателем
Проще всего определяется степень с натуральным (то есть целым положительным) показателем.
Выражения «возвести в квадрат» и «возвести в куб» нам давно знакомы.
Возвести число в квадрат — значит умножить его само на себя.
Возвести число в куб — значит умножить его само на себя три раза.
Возвести число в натуральную степень — значит умножить его само на себя раз:
Степень с целым показателем
Показатель степени может быть не только натуральным (то есть целым положительным), но и равным нулю, а также целым отрицательным.
Определим также, что такое степень с целым отрицательным показателем.
Заметим, что при возведении в минус первую степень дробь переворачивается.
Свойства арифметического квадратного корня:
Кубический корень
Обратите внимание, что корень третьей степени можно извлекать как из положительных, так и из отрицательных чисел.
Заметим, что корень третьей, пятой, девятой — словом, любой нечетной степени, — можно извлекать как из положительных, так и из отрицательных чисел.
Квадратный корень, а также корень четвертой, десятой, в общем, любой четной степени можно извлекать только из неотрицательных чисел.
Сразу договоримся, что основание степени больше 0.
При этом также выполняется условие, что больше 0.
Запомним правила действий со степенями:
— при перемножении степеней показатели складываются
— при делении степени на степень показатели вычитаются
— при возведении степени в степень показатели перемножаются
Ты нашел то, что искал? Поделись с друзьями!
Покажем, как применяются эти формулы в заданиях ЕГЭ по математике:
Внесли все под общий корень, разложили на множители, сократили дробь и извлекли корень.
Здесь мы записали корни в виде степеней и использовали формулы действий со степенями.
Это полезно
В нашей статье вы найдете всю необходимую теорию для решения задания №9 ЕГЭ по теме «Графики функций». Это задание появилось в 2022 году в вариантах ЕГЭ Профильного уровня.
Степени и корни в математике с примерами решения и образцами выполнения
Возведение в степень — это арифметическая операция, первоначально определяемая как результат многократного умножения числа на себя.
Арифметическим квадратным корнем из неотрицательного числа a называется такое неотрицательное число, квадрат которого равен a.
Что такое степень и корень, как сложить, перемножить, поделить степени, как возвести степень в степень и извлечь корень из степени. Как сложить, перемножить, поделить корни, как возвести в степень и извлечь корень из корня. И как вычислить корень из целого числа, когда он извлекается.
Степени с натуральными показателями
Пусть а — произвольное действительное число, а n — число. Произведение
n сомножителей, равных а, называется n-й степенью числа а и обозначается через 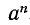
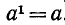
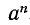
1) При любых натуральных n, m
Это следует из записи
Таким образом, при умножении степеней с одинаковыми основаниями показатели степени складываются.
2) Если 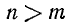
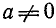
Действительно, это следует из равенства
3) При любых натуральных m, n
Действительно, по определению n-й степени числа имеем
и по свойству 1)
что и требовалось получить.
Итак, при возведении степени в степень показатели степени перемножаются.
Доказательство свойств 4) и 5) предоставляется читателю.
Степени с целыми показателями
Свойство 2) п. 9:
установлено при n > m. При n = m или n
Степень числа 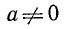
Нулевая и отрицательная степени числа 0 не определяются.
Определение (10.2) делает равенство (9.2) верным и при n
Нетрудно проверить, что все правила действия возведения в натуральную степень, указанные в п. 9, сохраняют силу при введенных определениях и при любых целых показателях степени.
Так, например, проверяем, что
т. е. и для отрицательных показателен степени сохраняет силу правило 1) умножения степеней с одинаковыми основаниями.
Пример:
Вычислить:
Решение:
Используем то, что 
Корни
Если n > 1—натуральное число, а а и b — действительные числа, причем
то число b называется корнем n-й степени из числа а. Таким образом, корнем n-й степени из числа а называется каждое число b такое, что его n-я степень равна а.
Если n — нечетное число, то, как можно доказать, для любого действительного числа а существует единственное значение корня степени n (в действительной области; извлечение корней в области комплексных чисел рассматривается в п. 18).
Если n — четное, то действие извлечения корня степени n из отрицательного числа невозможно, так как четная степень любого числа неотрицательна. Можно показать, что для любого положительного числа а корень четной степени n имеет два значения, равных по абсолютной величине и противоположных по знаку. Например, числа +3, —3 суть корни квадратные из числа 9. Положительный корень четной степени нз положительного числа называется арифметическим корнем (или арифметическим значением корня). Его единственность видна из такого соображения. Если бы имеюсь два положительных корня 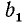
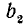
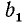
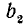
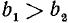
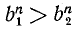
Наметим обоснование утверждения о существовании корня 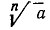
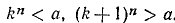
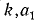
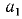
Далее будем искать приближение корня в виде дроби с двумя знаками после запятой и т. д. Таким путем в принципе можно построить ряд десятичных приближений по недостатку и по избытку для некоторого действительного числа, которое и следует принять за значение искомого корня (аналогично примеру 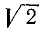
Корень степени n обозначается с помощью знака радикала 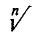
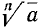
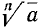
1) единственное значение корня в случае нечетного n (а в этом случае — любое действительное число).
2) арифметический корень степени n из а в случае четного а (в этом случае а > 0).
Корень из нуля при любом показателе n равен нулю.
В случае, если мы хотим рассматривать оба значения корня четной степенн из положительного числа, то пишем 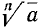
В случае корня степени 2 (квадратного корня) пишут просто 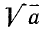
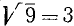
Если а — произвольное действительное число, то
при нечетном n и
при четном n (в частности, в случае квадратного корня). Так, например, 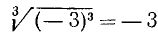
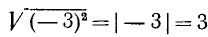
Укажем основные правила действий над корнями; для простоты предположим, что числа под знаком корня—положительные.
1) Извлечение корня из произведения. Корень из произведения равен произведению корней из сомножителей:
Доказательство:
Для доказательства этого (и дальнейших) свойства достаточно проверить, что при возведении обеих частей равенства (11.1) в степень m получим одно и то же число. При этом мы пользуемся соотношением 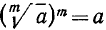
откуда и вытекает требуемое свойство.
2) Возведение корня в степень. Для возведения корня в степень достаточно возвести в, эту степень подкоренное выражение, сохраняя показатель корня.
Это правило записывается так:
Свойство 2) непосредственно вытекает из свойства 1), а также может быть проверено возведением обеих частей равенства (11.2) в степень m.
3) Извлечение корня из частного. Корень из частного равен частному от деления корня из числителя на корень из знаменателя:
4) Извлечение корня из степени. Пусть показатель степени m является кратным показателя корня n: m = nk. Тогда
т. е. при извлечении корня из степени показатель степени следует разделить на показатель корня.
Пусть в общем случае m не является кратным n; выполним деление m на n с остатком: m = nq + r. Тогда
Действительно, применяя уже найденные правила, получим
Пример:
5) Извлечение корня из корня. Для извлечения корня из корня достаточно перемножить показатели корней, сохранив подкоренное выражение:
6) Сокращение показателя корня и показателя подкоренного выражения на их общий множитель. Пусть в выражении 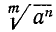
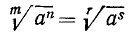
Обратно, если показатели корня и подкоренного выражения умножить на одно и то же число, то корень от этого не изменится. Например:
7) Приведение корней к общему показателю. Пользуясь только что установленным свойством, можно два или несколько корней приводить к общему показателю, который представляет собой н. о. к. показателей всех данных корней.
Это преобразование полезно применять при умножении корней с разными показателями.
Пример:
Упростить произведение
Решение:
Здесь н. о. к. показателей корней равнялось 6; в процессе преобразования мы применили также правило 6) сокращения показателей степени и корня и правило 1).
Аналогичным образом выполняется и деление корней.
Пример:
Степени с рациональными показателями
Степени с действительными показателями. Будем, как и в п. 11, рассматривать только корни из положительных чисел. Мы видели, что в случае, когда m делится нацело на n,
Обобщая это правило, можно ввести следующее определение степени с положительным рациональным показателем p/q:
В случае отрицательного рационального показателя степени —p/q полагают (по аналогии со случаем целого отрицательного показателя степени)
На степени с рациональными показателями распространяются все правила действий над степенями с натуральными и вообще целыми показателями. Для их обоснования достаточно применить правила п. 11 действий над корнями. Докажем, например, свойство
Так же получим 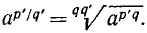
что и требовалось доказать.
Рассматривают также степени положительного числа а при произвольных действительных показателях. В основу определения 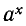
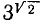
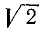
По мере продолжения этого процесса левая и правая части неравенств, выраженные бесконечными десятичными дробями, будут иметь все большее и большее число совпадающих десятичных знаков, которые и будут приниматься за десятичные знаки, определяющие иррациональное число 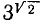
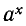
Замечание:
Извлечение корня нечетной степени возможно и из отрицательного числа. Поэтому выражению 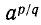
Алгоритм извлечения квадратного корня
Пусть дано произвольное положительное число А; тогда можно указать последовательность арифметических действий, приводящую к вычислению квадратного корня из данного числа с любой заданной степенью точности. Эта последовательность действий, описанная ниже, получает название алгоритма извлечения квадратного корня.
Предположим вначале для простоты, что данное число — целое m-значное; записываем его в виде 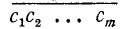
Таким образом, если А — одно- или двузначное число, то целая часть 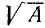
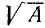
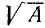
Число граней и дает нам число цифр целой части 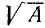
Следующий шаг состоит в определении первой цифры числа 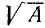
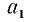
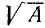
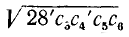
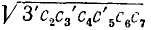
Покажем, из каких соображений можно находить следующую цифру 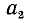
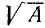
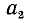
Можно было бы находить 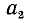
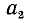
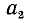
Такое 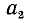
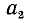
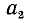
При этом 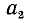
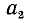
Пример:
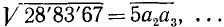
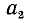
Наибольшее значение 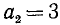
Так как неравенство выполнено, то вторая цифра корня равна 3:
Пример:
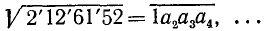
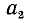
Наибольшее возможное значение
неверно. Испытываем 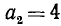
Неравенство выполнено. Итак,
Замечание:
Здесь практически можно было определить первые две цифры корня сразу, в уме, так как очевидно, что
После того как найдены первые две цифры корня 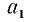
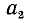
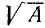
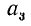
получая из него оценку для 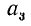
При практическом извлечении корня все вычисления располагают в некоторой определенной схеме, которую мы напомним на тех же примерах 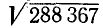
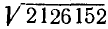
Перед разбором примеров приведем для удобства формулировку правила извлечения корня.
Правило. Чтобы извлечь квадратный корень из данного целого числа, разбивают его справа налево на грани, по две цифры в каждой, кроме первой (крайней левой), в которой может быть и одна цифра.
Чтобы найти первую цифру корня, извлекают квадратный корень из первой грани.
Чтобы найти вторую цифру, из первой грани вычитают квадрат первой цифры корня, к остатку сносят вторую грань и число десятков получающегося числа делят на удвоенную первую цифру корня; полученное целое число подвергают испытанию.
Испытание это производится так: за вертикальной чертой корня (налево от остатка) пишут удвоенное ранее найденное число корня и к нему с правой стороны приписывают испытуемую цифру; получившееся после этой приписки число умножают на испытуемую цифру. Если после умножения получится число, большее остатка, то испытуемая цифра не годится и надо испытывать следующую, меньшую цифру.
Следующие цифры корня находят с помощью того же приема.
Если после снесения грани число десятков получившегося числа окажется меньше делителя, т. е. меньше удвоенной найденной части корня, то в корне ставят 0, сносят следующую грань и продолжают действие дальше.
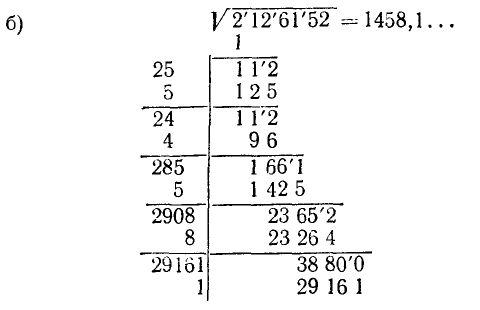
Пример:
Вычислить: а) 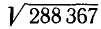
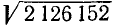
Решение:
Примечания:
*) Цифра 7 не выдерживает испытания; переходим к следующей цифре 6. **) Мысленно дополняем подкоренное число нулями за запятой и сносим следующую нулевую грань.
Если подкоренное число выражается десятичной дробью, то деление на грани производится от запятой: для целой части влево, для дробной — вправо:
в остальном процесс извлечения корня остается тем же.
Степени с целым показателем
Мы определили выше степень с натуральным показателем. Ясно, что это определение не годится ни для целых отрицательных, ни для дробных показателей — нельзя взять число сомножителем ни —5, ни 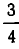
В физике часто встречаются величины, обладающие следующим свойством: за равные промежутки времени величина изменяется в одно и то же число раз. Например, если за первый час своего изменения величина уменьшилась втрое, то и за десятый час она тоже уменьшится втрое. Примером такой величины является масса радиоактивного вещества. Пусть в начале наблюдения был 1 кг этого вещества, а после первых суток осталось а кг, то есть количество вещества изменилось в а раз. Тогда, как показывают опыты, в течение вторых суток количество вещества тоже изменится в а раз. Поэтому после вторых суток останется 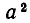
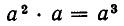
Таким же образом изменяются все остальные величины, обладающие указанным выше свойством. Именно если в начале наблюдения значение этой величины равняется М, а через 1 единицу времени это значение изменилось в а раз и стало равно Ма, то через n единиц времени значение величины равно
Поскольку величина промежутка времени стоит в показателе формулы (1), закон изменения (1) называют показательным.
Формула (1) не дает ответа на вопросы, чему равно значение величины через 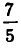
Естественно обозначить значение величины через t единиц времени после начала наблюдения так: 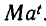
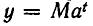
При обобщении понятия степени мы будем руководствоваться следующим требованием.
Для степеней с любыми показателями должны оставаться в силе основные свойства степеней с натуральными показателями:
Иными словами, эти свойства должны оставаться справедливыми не только для натуральных, но и для любых показателей. Обычно мы будем пользоваться одним из этих свойств для введения соответствующего определения, после чего будем проверять выполнение остальных свойств.
Отметим, что два подхода — с точки зрения физики и с точки зрения математики — согласуются друг с другом.
Выясним физический смысл свойств 3) и 5). Пусть сначала прошло m единиц времени, а потом n единиц времени. За первые m единиц времени величина изменится в 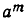
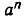
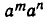
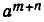
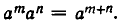
Аналогично истолковывается смысл свойства 5). Примем m единиц времени за новую единицу измерения (например, перейдем от секунд к минутам или часам). Тогда за одну новую единицу измерения времени наша величина изменяется в 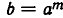
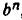
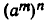
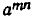
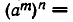
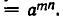
Степень с нулевым показателем
Пока что оно имеет смысл лишь при натуральных значениях n. Выясним, как надо определить 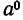
Отсюда ясно, что при 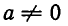
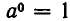
Проверим, согласуется ли это определение с физическим подходом. Мы рассматриваем величины, которые в момент времени t принимают значение 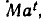
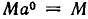
Степень с целым отрицательным показателем
Определим степень с целым отрицательным показателем — n (то есть 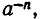
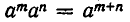
Отсюда следует, что при 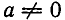
При а =0 выражение 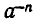
Мы распространили понятие степени на случай любого целого показателя — положительного, отрицательного и нулевого. Покажем, что при этом выполняются свойства 1) — 5) степеней, сформулированные в п. 1 (при этом, конечно, основания степеней должны отличаться от нуля).
Докажем, что выполняется равенство 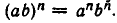
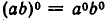
Но 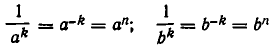
Тем самым доказано выполнение равенства 1) и при целых отрицательных значениях n.
Точно так же доказывается выполнение равенства
Предоставляем читателю разобрать остальные случаи (включая и те, когда одно из чисел m, n, m+n обращается в нуль). Доказательство равенства 4)
проводится тем же способом.
Наконец, докажем соотношение 5): 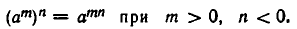
Случаи, когда m и n имеют иные знаки или обращаются в нуль, разбираются точно так же. Например, 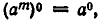
Итак, для степеней с любым целым показателем выполняются свойства 1) — 5) из п. 1. Отметим еще некоторые свойства этих степеней.
Если а — положительное число, то для всех целых значений n число 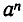
Имеют место равенства:
(здесь k обозначает любое целое число). Отсюда следует, что если а — отрицательное число, то 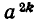
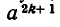
Примеры:
Сначала выполним указанные действия, а потом освободимся от отрицательных показателей. Итак, наше выражение равно:
Корни. Степени с рациональными показателями
Пусть а — положительное число и n — натуральное число. Можно доказать, что существует одно и только одно положительное число b такое, что 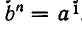
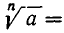
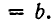
обозначают одно и то же.
Число а называют подкоренным выражением, а n—показателем корня. Принято при n = 2 опускать показатель корня. Поэтому 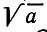
Отметим, что наряду со словом «корень» употребляют слово «радикал». Мы будем применять этот термин в тех случаях, когда корень из числа можно спутать с корнем уравнения.
Введем понятие алгебраического корня. Говорят, что число b является алгебраическим корнем n-й степени из числа а, если 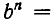
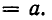
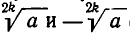
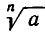
Так как четная степень любого действительного числа неотрицательна, то из отрицательного числа нельзя извлечь действительного корня четной степени. Позже мы познакомимся с комплексными числами, введение которых позволяет определять корни четной степени и из отрицательных чисел.
Если n=2k+1 — нечетное число, то из любого действительного числа а можно извлечь корень степени n. Именно если а >0, то этим корнем является 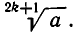
Степени с рациональными показателями
Были определены степени с любыми целыми показателями. Обобщим далее понятие степени, введя степени с любыми рациональными показателями. Это обобщение тесно связано с понятием корня.
Пусть r — рациональное число и а — положительное число. Запишем число r в виде дроби 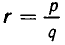
Нам надо определить выражение 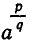
Из него следует, что 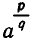
Мы ограничиваемся при этом арифметическими значениями корней
При 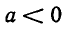
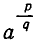
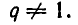
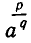
В следующем пункте мы выведем свойства степеней с рациональными показателями. Нам понадобятся для этого следующие два утверждения. а) Если а и b — положительные числа, причем а>b, и если n — натуральное число, то
Докажем это утверждение индукцией по n. При n = 1 оно имеет место. Пусть уже доказано, что 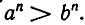
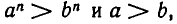


Другое доказательство этого неравенства следует из тождества
Если а > b, а > 0 и b>0, то обе скобки в правой части равенства положительны и потому
Из свойства а) непосредственно вытекает следующее утверждение:
б) Если а и b — такие положительные числа, что для некоторого натурального числа n имеем
В самом деле, если бы мы имели, например, а >b, то по свойству а) выполнялось бы неравенство 
Каждое рациональное число можно различными способами записать в виде дроби. Например, 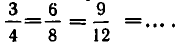
Для этого возведем обе части равенства (4) в степень qn. В силу свойства 5) степеней с натуральным показателем и равенства (1) имеем:
С другой стороны, по формуле (1),
Таким образом, qn-е степени обеих частей доказываемого равенства (4) совпадают. В силу утверждения б) отсюда вытекает справедливость равенства (4).
Можно доказать, что определение (2) согласуется с физическим смыслом степеней с показателем 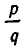
Свойства степеней с рациональными показателями
Докажем, что для степеней с рациональными показателями сохраняются основные свойства степеней с натуральными показателями.
Сначала докажем, что при х >О, у >0 и любом рациональном r
Пусть 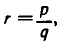
Возведем обе части равенства (1′) в степень q. В силу формулы (I), п. 2, и свойства 1) степеней с натуральным показателем имеем:
Мы доказали, что q-е степени обеих частей доказываемого равенства (1) имеют одно и то же значение 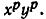
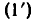
Совершенно так же доказывается, что если х > 0 и у > 0, а r — рациональное число, то
Теперь докажем, что при х > 0 для любых рациональных чисел г, и г2 выполняется равенство:
Сначала рассмотрим случай, когда 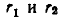
В этом случае доказываемое равенство принимает вид:
Возведем обе части этого равенства в степень q. Мы получим, что
С другой стороны
Таким образом, q-е степени обеих частей равенства (4) имеют одно и то же значение 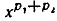
Итак, равенство (3) доказано для случая, когда 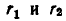
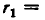
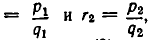
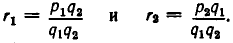
Совершенно так же доказывается выполнение равенства
для положительных х и рациональных
Наконец, докажем, что если х — положительное число и 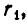
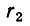
В самом деле, пусть 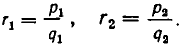
Для этого возведем обе части равенства (7) в степень 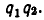
Так как 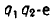
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института