что такое кориолисово ускорение

iSopromat.ru

Ускорение Кориолиса (Кориолисово ускорение) характеризует изменение относительной скорости по направлению за счет переносного вращения и изменение величины переносной скорости за счет относительного движения.

Согласно теореме Кориолиса, абсолютное ускорение точки в сложном движении определяется как геометрическая сумма относительного, переносного и кориолисова ускорений (рис. 3)

Поскольку, в данном случае, относительное движение происходит по прямой линии, относительное ускорение a_r направлено вдоль этой прямой и определяется выражением

Переносным ускорением точки M является ускорение точки M диска. Диск совершает вращательное движение, следовательно, переносное ускорение определяется выражением

где a_e вр = ε ⋅ OM — вращательное ускорение точки M, направленное перпендикулярно отрезку OM;
a_e цс = ω 2 ⋅ OM — центростремительное ускорение точки M, направленное к центру диска.

Ускорение Кориолиса или поворотное ускорение определяется по формуле

где ω_e — переносная угловая скорость,
ν_r — относительная скорость точки.

Направление ускорения Кориолиса определяется по правилу векторного произведения или по правилу Жуковского.

Величина ускорения Кориолиса определяется выражением

где α – угол между векторами ω_e и ν_r.

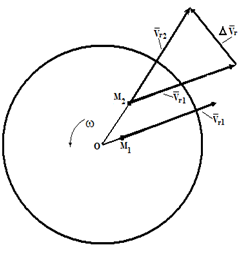
Рассмотрим, какой физический смысл заложен в ускорение Кориолиса. Для простоты будем считать, что диск вращается с постоянной угловой скоростью, а точка M движется относительно диска с постоянной относительной скоростью (рис.4).

Пусть в момент времени t₁ точка M занимала положение M₁ и имела относительную скорость ν_r1. За промежуток времени Δt точка M переместится в положение M₂, при этом направление скорости ν_r изменится вследствие вращения диска. Вектор ν_r получит приращение Δν_r. Отношение Δν_r/Δt определяет среднее ускорение точки за промежуток времени Δt. Предел отношения Δν_r / Δt при Δt → 0 есть производная dν_r /dt, как производная от вектора постоянного по величине.

Рассмотрим, как изменяется переносная скорость в зависимости от относительного движения. В моменты времени t₁ и t₂ переносная скорость определяется выражениями ν_e1= ω × OM₁ и ν_e2= ω × OM₂. Тогда приращение вектора ν_e за счет относительного движения будет равно

Отношение Δν_e/ Δt в пределе при Δt → 0 дает производную dν_e / dt = ω × ν_r.

Таким образом, ускорение Кориолиса с одной стороны характеризует изменение относительной скорости по направлению за счет переносного вращения и, с другой стороны, изменение величины переносной скорости за счет относительного движения.

Абсолютное ускорение точки в сложном движении в общем случае определяется геометрической суммой пяти слагаемых

Для определения величины абсолютного ускорения удобнее пользоваться аналитическим методом сложения векторов:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Кориолисово ускорение: определение, причина возникновения, формула, влияние на земные процессы

Когда в физике изучают процесс движения тел в неинерциальных системах отсчета, то приходится учитывать так называемое кориолисово ускорение. В статье мы дадим ему определение, покажем, по какой причине оно возникает и где проявляется на Земле.

Что такое кориолисово ускорение?

Если отвечать коротко на этот вопрос, то можно сказать, что это то ускорение, которое возникает в результате действия силы Кориолиса. Последняя проявляет себя, когда тело движется в неинерциальной вращающейся системе отсчета.

Вам будет интересно: Интенсивность звука, его сила и поток звуковой энергии

Напомним, что неинерциальные системы движутся с ускорением или вращаются в пространстве. В большинстве физических задач наша планета полагается инерциальной системой отсчета, поскольку ее угловая скорость вращения слишком мала. Однако, при рассмотрении данной темы Земля полагается неинерциальной.

Вам будет интересно: Заковский Леонид Михайлович: краткая биография, настоящее имя, служба в органах госбезопасности, дата и причина смерти

Сила Кориолиса и направления движения в пространстве

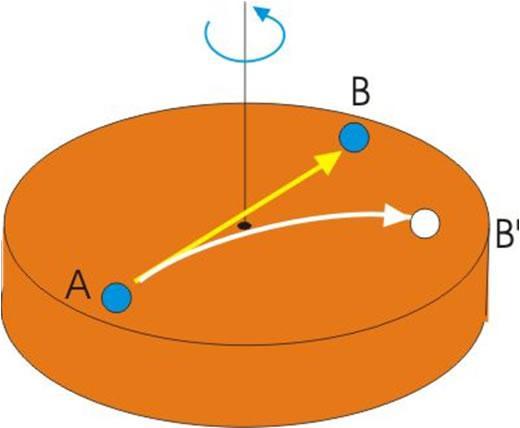
Представим себе вращающийся в горизонтальной плоскости диск. Через его центр проходит вертикальная ось вращения. Пусть на диске относительно него покоится тело. В состоянии покоя на него действует центробежная сила, направленная по радиусу от оси вращения. Если не существует центростремительной силы, которая ей противодействует, то тело слетит с диска.

Теперь предположим, что тело начало двигаться вертикально вверх, то есть параллельно оси. В этом случае его линейная скорость вращения вокруг оси будет равна таковой для скорости диска, то есть никакой кориолисовой силы не будет возникать.

Если тело начало совершать радиальное движение, то есть начало приближаться или удалятся от оси, то появляется сила Кориолиса, которая будет направлена по касательной к направлению вращения диска. Ее появление связано с сохранением момента импульса и с наличием некоторой разности в линейных скоростях точек диска, которые находятся на разном расстоянии от оси вращения.

Наконец, если тело будет перемещаться по касательной к вращающемуся диску, то появится дополнительная сила, которая будет его толкать либо к оси вращения, либо от нее. Это радиальная компонента силы Кориолиса.

Поскольку направление кориолисова ускорения совпадает с направлением действия рассмотренной силы, то это ускорение также будет иметь две компоненты: радиальную и тангенциальную.

Формула силы и ускорения

Сила и ускорение в соответствии со вторым ньютоновским законом связаны друг с другом следующим соотношением:

Если рассмотреть пример выше с телом и вращающимся диском, то можно получить формулу для каждой компоненты кориолисовой силы. Для этого следует применить закон сохранения углового момента, а также вспомнить формулу для центростремительного ускорения и выражение связи угловой и линейной скорости. В итоге, кориолисова сила может быть определена следующим образом:

В квадратных скобках стоит векторное произведение скоростей. Оно содержит ответ на вопрос, куда направлено кориолисово ускорение. Его вектор направлен перпендикулярно и оси вращения, и линейной скорости перемещения тела. Это означает, что изучаемое ускорение приводит к искривлению прямолинейной траектории движения.

Влияние силы Кориолиса на полет пушечного ядра

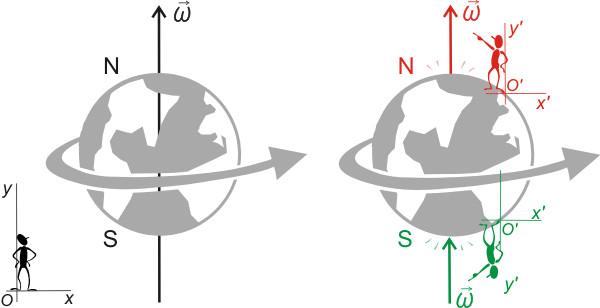
Чтобы лучше понять, как на практике проявляет себя изучаемая сила, рассмотрим следующий пример. Пусть пушка, находясь на нулевом меридиане и нулевой широте, выполняет выстрел строго на север. Если бы Земля не вращалась с запада на восток, то ядро упало бы на долготе 0°. Однако из-за вращения планеты ядро упадет на другой долготе, смещенной к востоку. Это и есть результат действия кориолисова ускорения.

Объяснение описанного эффекта простое. Как известно, точки на поверхности Земли вместе с воздушными массами над ними имеют большую линейную скорость вращения, если они находятся в низких широтах. При вылете из пушки ядро обладало большой линейной скоростью вращения с запада на восток. Эта скорость приводит к его смещению в восточном направлении при полете в более высоких широтах.

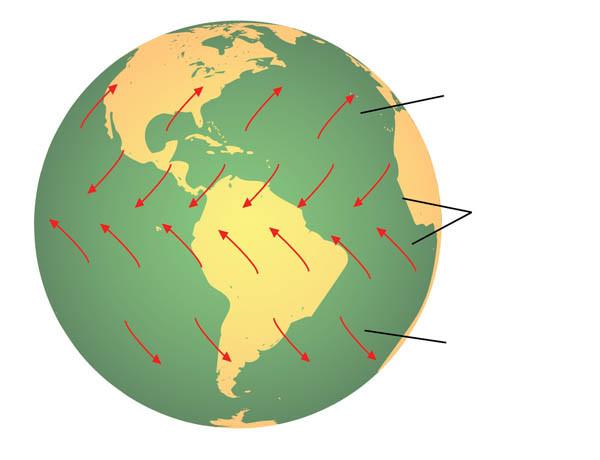
Эффект Кориолиса и морские и воздушные течения

Ярче всего влияние силы Кориолиса прослеживается на примере океанских течений и на движении воздушных масс в атмосфере. Так, течение Гольфстрим, начинаясь на юге Северной Америке, пересекает весь Атлантический океан и достигает берегов Европы благодаря отмеченному эффекту.

Что касается воздушных масс, то ярким проявлением влияния силы Кориолиса являются ветра пассаты, которые круглый год дуют с востока на запад в низких широтах.

Пример задачи

Выше была записана формула для ускорения Кориолиса. Необходимо с ее использованием вычислить величину ускорения, которое приобретает тело, двигаясь со скоростью 10 м/с, на широте 45°.

Чтобы пользоваться формулой для ускорения применительно к нашей планете, следует добавить в нее зависимость от широты θ. Рабочая формула будет иметь вид:

Знак минус был опущен, поскольку он определяет направление ускорения, а не его модуль. Для Земли ω = 7,3*10-5 рад/с. Подставляя все известные числа в формулу, получаем:

a = 2*7,3*10-5*10*sin(45o) = 0,001 м/с2.

Как видно, рассчитанное кориолисово ускорение практически в 10 000 раз меньше ускорения свободного падения.

Источник

Ускорение и сила Кориолиса – что это?

Опубликовано 19 Фев 2014
Рубрика: Механика | 2 комментария

Из этой статьи вы не узнаете ничего нового о крутых правых берегах рек северного полушария, о направлениях вращения атмосферных циклонов и антициклонов, о пассатах и о закручивании воды в сливном отверстии ванны или раковины. Эта статья расскажет вам об.

. истоках понятий «ускорение Кориолиса» и «сила Кориолиса».

Прежде чем начать отвечать на вопрос заголовка статьи я хочу напомнить несколько определений. Для упрощения понимания при изучении сложных движений тел в теоретической механике были введены понятия относительного движения и переносного, а так же присущих им скоростей и ускорений.

Относительное движение характеризуется относительной траекторией, относительной скоростью v_отн и относительным ускорением a_отн и представляет собой движение материальной точки относительно подвижной системы координат.

Далее в тексте статьи для отличия векторных величин от абсолютных значений приняты следующие обозначения:

Приношу извинения за отступление от использования общепринятых символов в обозначении векторов.

Основные формулы сложного движения материальной точки в векторной форме:

v — = v_отн — + v_пер —

a — = a_отн — + a_пер — + a_кор —

Если относительное ускорение является параметром изменения относительной скорости в относительном движении материальной точки, переносное ускорение – параметром изменения переносной скорости в переносном движении, то ускорение Кориолиса характеризует изменение относительной скорости точки в переносном движении и переносной скорости в относительном движении. Непонятно? Разберемся, как обычно, на примере!

Как возникает ускорение Кориолиса

ω_пер = const ε_пер = 0

v_отн = const a_отн = 0

2. Как можно догадаться по аббревиатурам – относительное движение в нашем примере – это прямолинейное движение ползуна — точки C — по кулисе, а переносное движение – это вращение ползуна вместе кулисой вокруг центра – точки О. Ось x₀ – ось неподвижной системы координат.

3. То, что ускорения ε _пер = 0 и a _отн = 0 выбрано в примере не случайно. Это облегчит и упростит восприятие и понимание сути и природы возникновения кориолисова ускорения и рождаемой этим ускорением – силы Кориолиса.

4. При переносном движении (вращении кулисы) вектор относительной линейной скорости v_отн1 — повернется за малый промежуток времени dt на весьма незначительный угол dφ и получит при этом приращение (изменение) в виде вектора dv_отн — _.

dφ = ω_пер * dt

dv_отн — = v_отн2 — — v_отн1 —

dv _отн = v _отн * dφ = v _отн * ω _пер * dt

8. При относительном движении (прямолинейном перемещении точки C ползуна по кулисе) вектор переносной линейной скорости v_пер — за незначительный промежуток времени dt переместится на расстояние dS и получит приращение (изменение) — вектор dv_пер — _.

dS = v _отн * dt

dv_пер — = v_пер2 — — v_пер1 — — dv ц _пер —

dv _пер = ω _пер * dS = ω _пер * v _отн * dt

9. Вектор переносной скорости точки C v_пер2 — в положении №2 увеличил свой размер и сохранил направление относительно подвижной системы координат – оси x. В неподвижной системе координат (ось x₀) этот вектор повернулся за счет переносного движения на угол dφ и переместился на расстояние dS благодаря переносному движению!

11. Появление вектора изменения переносной скорости dv ц _пер — в ызвано переносным движением (вращением)! На точку C действует переносное ускорение a_пер – в нашем случае центростремительное, вектор которого направлен к центру вращения точке O.

В нашем примере это ускорение действует и в начальный момент времени (в положении №1), его значение равно:

a_кор — = a₁ — + a₂ —

13. Основные зависимости скорости и ускорения точки C в неподвижной системе координат в векторной и абсолютной формах для нашего примера выглядят так:

v — = v_отн — + v_пер —

v = ( v_отн 2 + ω_пер 2 * S 2 ) 0,5

a — = a_пер — + a_кор —

a = ( ω_пер 4 * S 2 + a_кор 2 ) 0,5 = ( ω_пер 4 * S 2 + 4 * ω_пер 2 * v_отн 2 ) 0,5

Итоги и выводы

Ускорение Кориолиса возникает при сложном движении точки только при одновременном выполнении трех независимых условий:

1. Переносное движение должно быть вращательным. То есть угловая скорость переносного движения должна быть не равна нулю.

2. Направление относительного движения не должно быть параллельно оси переносного вращения.

3. Относительное движение должно быть поступательным. То есть линейная скорость относительного движения не должна быть равна нулю.

Для определения направления вектора ускорения Кориолиса необходимо повернуть вектор линейной относительной скорости на 90° в сторону переносного вращения.

Если точка обладает массой, то согласно второму закону Ньютона кориолисово ускорение совместно с массой создадут силу инерции, направленную в сторону противоположную вектору ускорения. Это и есть сила Кориолиса!

Именно сила Кориолиса, действуя на некотором плече, создает момент, который называется гироскопическим моментом!

О гироскопических явлениях можно прочитать в целом ряде других статей этого блога.

Подписывайтесь на анонсы статей в окнах, расположенных в конце каждой статьи или вверху каждой страницы, и не забывайте подтверждать подписку.

В этой статье мне, как всегда, хотелось кратко и доходчиво рассказать о весьма непростых понятиях – об ускорении и силе Кориолиса. Удалось это или нет с интересом прочту в Ваших комментариях, уважаемые читатели!

Статьи с близкой тематикой

Отзывы

2 комментария на «Ускорение и сила Кориолиса – что это?»

Работа силы Кориолиса.

Одно из проявлений силы Кориолиса в природе, является формирование водоворотов циклонов и антициклонов. И чтобы в полной мере проявилась сила Кориолиса, должна произойти разбалансировка линейной и угловой скорости, как относительно оси Земли, так и относительно оси Солнца. Сила Кориолиса, также зависит от наклона оси Земли, к плоскости орбиты Земли. И без учета орбитального вращения Земли и наклона оси Земли, сила Кориолиса, останется в науке, как декорация, бесполезная для научно-практического применения, и задача для развития мышления у школьников. При кажущейся простоте сила Кориолиса для восприятия крайне трудна. И объективно изучать и анализировать её без макета Солнечной системы невозможно.

Воды озер, морей и океанов, северного полушария, вращаются против часовой стрелки, а воды южного полушария, вращаются по часовой стрелке, образуя гигантские водовороты. А все что вращается, в том числе и водовороты, обладают свойством гироскопа(юлы), сохранять вертикальное положение оси в пространстве независимо от вращения Земли. Если смотреть на Землю со стороны Солнцa, водовороты вращаясь вместе с Землей опрокидываются, два раза в сутки, благодаря чему, водовороты прецессируют, (1-2 градусов) и отражают от себя приливную волну. Воды Белого моря, вращаются против часовой стрелки, образуя огромный водоворот-гироскоп, прецессируя отражающий приливную волну по всему периметру Белого моря. Аналогичная схема приливов и отливов, наблюдается во всех озерах, морях и океанах. Приливную волну реке Амазонка, создает огромный планетарный водоворот диаметром несколько тысяч км, вращающийся между Южной Америкой и Северной Африкой, охватывая и устье реки Амазонка. Ширина приливной волны, зависит от диаметра водоворота. А высота приливной волны, зависит от скорости опрокидывания водоворота (за 12часов), и скорости вращения водоворота. А скорость вращения водоворота, зависит от силы Кориолиса, от осевой и орбитальной скорости Земли, и от наклона оси Земли. А роль Луны косвенная, создание неравномерной орбитальной скорости Земли. Воды Средиземного моря, вращаются против часовой стрелки, образуя приливы высотой 10-15 см. Но в заливе Габес, что у побережья Туниса, высота приливов достигает трех метров, а порой и больше. И это считается одной из загадок природы. Но в тоже время, в заливе Габес, вращается водоворот, прецессируя отражающий дополнительную приливную волну. Внутри постоянных океанических и морских водоворотов, вращаются небольшие постоянные и непостоянные вихри и водовороты, создаваемые впадающими в бухты реками, очертанием берегов и местными ветрами. И в зависимости от скорости, и направления вращения небольших прибрежных водоворотов, зависит календарь, амплитуда, и количество приливов и отливов в сутки. Водоворотную гипотезу приливов легко проверить по связи высоты приливной волны со скоростью вращения водоворотов. По высоте приливной волны, можно определять местонахождение водоворотов. Как правило положительные отзывы к гипотезе, пишут мыслители знающие о противоречиях в Лунной теории приливов и отливов, обладающие углубленными знаниями небесной механики, и свойств гироскопа.

Водоворотную теорию о приливах можно легко проверить, по связи высоты приливной волны со скоростью вращения водоворотов.

Список морей, со средней скоростью вращения водоворотов более 0,5 км/час, и средней высотой приливной волны более 5 см:

Ирландское море. Северное море. Баренцево море. Море Баффина. Белое море. Берингово море. Охотское море. Аравийское море. Саргасово море. Гудзонов залив. Залив Мэн. Залив Аляска. и т.д.

Список морей, со средней скоростью вращения водоворотов менее 0,5 км/час, и средней высотой приливной волны менее 5 см:

Балтийское море. Гренландское море. Черное море. Азовское море. Каспийское море. Чукотское море. Карское море. Море Лаптевых. Красное море. Мраморное море. Карибское море. Японское море. Мексиканский залив. и т.д.

Примечание: Высота приливной волны (солитона), и амплитуда приливов и отливов, это не одно и тоже.

Источник

Что такое кориолисово ускорение

Сила Кориолиса

При движении тела относительно вращающейся системы отсчета, кроме центростремительной и центробежной сил, появляется еще одна сила, называемая силой Кориолиса или кориолисовой силой инерции (Г. Кориолис (1792 – 1843) – французский физик). Появление кориолисовой силы можно обнаружить на следующем примере. Возьмем горизонтально расположенный диск, который может вращаться вокруг вертикальной оси. Прочертим на диске радиальную прямую ОА (рис. 4.10). Сила Кориолиса не является «настоящей» в смысле механики Ньютона. При рассмотрении движений относительно инерциальной системы отсчета такая сила вообще не существует. Она вводится искусственно при рассмотрении движений в системах отсчета, вращающихся относительно инерциальных, чтобы придать уравнениям движения в таких системах формально такой же вид, что и в инерциальных системах отсчета. Чтобы заставить шарик катиться вдоль ОА, нужно сделать направляющую, выполненную в виде ребра. При качении шарика направляющее ребро действует на него с некоторой силой. Относительно вращающейся системы (диска), шарик движется с постоянной по направлению скоростью. 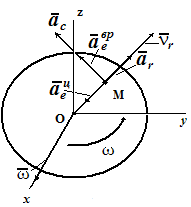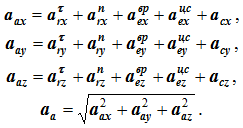Это можно объяснить тем, что эта сила уравновешивается приложенной к шарику силой инерции: (4.5.5) Здесь – сила Кориолиса, также являющаяся силой инерции, – угловая скорость вращения диска. Сила Кориолиса вызывает кориолисово ускорение. Выражение для этого ускорения имеет вид (4.5.6) Ускорение направлено перпендикулярно векторам и и максимально, если относительная скорость точки ортогональна угловой скорости вращения подвижной системы отсчета. Кориолисово ускорение равно нулю, если угол между векторами и равен нулю или π, либо если хотя бы один из этих векторов равен нулю. Следовательно, в общем случае, при использовании уравнений Ньютона во вращающейся системе отсчета, возникает необходимость учитывать центробежную, центростремительную силы инерции, а также кориолисову силу. Таким образом, всегда лежит в плоскости, перпендикулярной к оси вращения. Сила Кориолиса возникает только в случае, когда тело изменяет свое положение по отношению к вращающейся системе отсчета. Сила Кориолиса действует на тело, движущееся вдоль меридиана в северном полушарии вправо и в южном – влево (рис. 4.11). Это приводит к тому, что у рек подмывается всегда правый берег в северном полушарии и левый – в южном. Эти же причины объясняют неодинаковый износ рельсов железнодорожных путей. Силы Кориолиса проявляются и при качаниях маятника (маятник Фуко). Для простоты предположим, что маятник расположен на полюсе (рис. 4.12). На северном полюсе сила Кориолиса будет направлена вправо по ходу маятника. В итоге траектория движения маятника будет иметь вид розетки. Таким образом, вращение плоскости качаний маятника Фуко дает непосредственное доказательство вращения Земли вокруг своей оси. Если тело удаляется от оси вращения, то сила направлена противоположно вращению и замедляет его. Если тело приближается к оси вращения, то направлена в сторону вращения. С учетом всех сил инерции, уравнение Ньютона для неинерциальной системы отсчета (4.5.6) примет вид: (4.5.7) – сила инерции, обусловленная поступательным движением неинерциальной системы отсчета; – две силы инерции, обусловленные вращательным движением системы отсчета; – ускорение тела относительно неинерциальной системы отсчета: Источник ← что такое двухканальный роутер что такое квантовый человек → Вам также понравится что такое попуган игрушка 01.12.202326.04.2022 admin 0 что такое еда маки 05.12.202319.04.2022 admin 0 что такое опорный пункт в пожарной охране 07.12.202323.04.2022 admin 0 Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сохранить моё имя, email и адрес сайта в этом браузере для последующих моих комментариев.