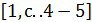что такое корень многочлена

Корень многочлена

Корень многочлена (не равного тождественно нулю)

над полем k — элемент , такой что выполняются два следующих равносильных условия:

Равносильность двух формулировок следует из теоремы Безу. В различных источниках любая одна из двух формулировок выбирается в качестве определения, а другая выводится в качестве теоремы.

Содержание

Свойства

Нахождение корней

Способ нахождения корней линейных и квадратичных многочленов, то есть способ решения линейных и квадратных уравнений, был известен ещё в древнем мире. Поиски формулы для точного решения общего уравнения третьей степени продолжались долгое время (следует упомянуть метод, предложенный Омаром Хайямом), пока не увенчались успехом в первой половине XVI века в трудах Сципиона дель Ферро, Никколо Тарталья и Джероламо Кардано. Формулы для корней квадратных и кубических уравнений позволили сравнительно легко получить формулы для корней уравнения четвертой степени.

То, что корни общего уравнения пятой степени и выше не выражаются при помощи рациональных функций и радикалов от коэффициентов было доказано норвежским математиком Нильсом Абелем в 1826 году. [1] Это совсем не означает, что корни такого уравнения не могут быть найдены. Во-первых, в частных случаях, при некоторых комбинациях коэффициентов корни уравнения при некоторой изобретательности могут быть определены. Во-вторых, существуют формулы для корней уравнений 5-й степени и выше, использующие, однако, специальные функции — эллиптические или гипергеометрические (см., к примеру, корень Бринга).

В случае, если все коэффициенты многочлена рациональны, то нахождение его корней приводится к нахождению корней многочлена с целыми коэффициентами. Для рациональных корней таких многочленов существуют алгоритмы нахождения перебором кандидатов с использованием схемы Горнера, причем при нахождении целых корней перебор может быть существенно уменьшен приемом чистки корней. Также в этом случае можно использовать полиномиальный LLL-алгоритм.

Для приблизительного нахождения (с любой требуемой точностью) вещественных корней многочлена с вещественными коэффициентами используются итерационные методы, например, метод секущих, метод бисекции, метод Ньютона. Количество вещественных корней многочлена на интервале может быть оценено при помощи теоремы Штурма.

Источник

Алгебра и начала математического анализа. 10 класс

Конспект урока

Алгебра и начала математического анализа, 10 класс

Урок №11. Многочлен P(x) и его корень. Алгебраическое уравнение.

Перечень вопросов, рассматриваемых в теме

1) обобщенное понятие многочлена;

2) основные действия над многочленами;

3) определение алгебраического уравнения;

Стоит отметить, что каждый многочлен степени больше 2 можно разложить на множители.

Корнем многочлена Р(х) называют такое значение х, при котором многочлен обращается в нуль.

Теорема Безу. Остаток от деления многочлена Р(х) на двучлен х-а равен Р(а).

Следствие. Если число а является корнем многочлена Р(х), то многочлен

где P — многочлен от переменных x₁, x₂, …, x_n, которые называются неизвестными.

Коэффициенты многочлена P обычно берутся из некоторого множества F, и тогда уравнение P(x₁, x₂, …, x_n)=0 называется алгебраическим уравнением над множеством F.

Степенью алгебраического уравнения называют степень многочлена P.

Значения переменных x₁, x₂, …, x_n, которые при подстановке в алгебраическое уравнение обращают его в тождество, называются корнями этого алгебраического уравнения.

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Общая теория многочленов многих переменных далеко выходит за рамки школьного курса.

Мы рассмотрим многочлены одной действительной переменной, да и то в простейших случаях. Рассмотрим многочлены одной переменной, приведённые к стандартному виду.

Стоит отметить, что каждый многочлен степени больше 2 можно разложить на множители.

Корнем многочлена Р(х) называют такое значение х, при котором многочлен обращается в нуль.

Алгебраическое уравнение (полиномиальное уравнение) — уравнение вида

где P — многочлен от переменных x₁, x₂, …, x_n, которые называются неизвестными.

Коэффициенты многочлена P обычно берутся из некоторого множества F, и тогда уравнение P(x₁, x₂, …, x_n)=0 называется алгебраическим уравнением над множеством F.

Степенью алгебраического уравнения называют степень многочлена P.

является алгебраическим уравнением четвертой степени от трёх переменных (с тремя неизвестными) над множеством вещественных чисел.

Значения переменных x₁, x₂, …, x_n, которые при подстановке в алгебраическое уравнение обращают его в тождество, называются корнями этого алгебраического уравнения.

Теорема Безу, невзирая на кажущуюся простоту и очевидность, является одной из базовых теорем теории многочленов. В данной теореме алгебраические характеристики многочленов (они позволяют работать с многочленами как с целыми числами) связываются с их функциональными характеристиками (которые позволяют рассматривать многочлены как функции).

Теорема Безу. Остаток от деления многочлена Р(х) на двучлен х-а равен Р(а).

Эту закономерность отметил и математик Безу.

Следствие. Если число а является корнем многочлена Р(х), то многочлен

Основные работы Этьенна Безу относятся к высшей алгебре, они посвящены созданию теории решения алгебраических уравнений.

В теории решения систем линейных уравнений он содействовал возникновению теории определителей, развивал теорию исключения неизвестных из систем уравнений высших степеней, доказал теорему (впервые сформулированную Маклореном) о том, что две кривые порядка m и n пересекаются не более чем в mn точках.

Во Франции и за её границей вплоть до 1848 года был очень популярен его шеститомный «Курс математики», написанный им в 1764-69 годах.

Безу развил метод неопределённых множителей. В элементарной алгебре его именем назван способ решения систем уравнений, основанный на этом методе.

Часть трудов Безу посвящена внешней баллистике.

Именем ученого названа одна из основных теорем алгебры.

Примеры алгебраических уравнений

Примеры и разбор решения заданий тренировочного модуля

Разложим на множители многочлен:

Решение: )

Ответ: ))

Источник

Определение корня многочлена

РЕФЕРАТ

Корни многочлена. Теорема Безу

Студенты 1 курса группы ИМ-11

Очного отделения

Шабунин Дмитрий Олегович

Зорин Александр Сергеевич

Бобылева Оксана Владимировна

1.2.Определение корня многочлена……………………………………………….4

1.4.Нахождение корней по схеме Горнера. Виды корней……………………….7

2. Этьен Безу. Биография. Теорема Безу. Следствия из теоремы……………….13

2.3 Следствия из теоремы Безу…………………………………………………..14

2.4. Примеры использования теоремы…………………………………………..14

Список используемых источников………………………………………………..17

ВВЕДЕНИЕ

Тема данного реферата: «Корни многочлена. Теорема Безу».

В нем мы хотим рассмотреть, что такое многочлен, что является корнем многочлена, а также рассказать про схему Горнера и теорему Безу.

В первой части мы разберем понятие многочлена, его корней и их виды и про схему Горнера. Во второй про теорему Безу.

Данная тема довольно актуальна, поскольку теорема Безу является одной из базовых теорем алгебры.

Многочлены

Понятие многочлена

Многочлен (полином) от одной переменной x – это выражение вида

,

2 члена называются подобными, если их степени равны. При этом подобные между собой члены можно преобразовать в один, т.е. привести подобные члены.

Степенью многочлена называют наибольшую среди степеней многочлена, при этом многочлен f(x)- не тождественный нуль. Обозначается эта степень deg(f).

-многочлен четвертой степени (старшая степень равна четырем);

— многочлен второй степени или квадратный (старшая степень равна двум).

При этом тождественный нуль степени не имеет.

Предполагается, что коэффициенты многочлена принадлежат определенному полю (полю действительных, рациональных, комплексных чисел). Так, если выполнять над многочленом операции сложения, умножения или вычитания при помощи сочетательного, переместительного и распределительных законов, мы получаем снова многочлен.

Из вышесказанного следует, что совокупность всех многочленов с коэффициентами из данного поля Р образует кольцо Р — кольцо многочленов над данным полем, это кольцо не имеет делителей нуля, т.е. произведение многочленов, не равных нулю, не может дать нуль.

Определение корня многочлена

Элемент кольца Р называется корнем многочлена f(x) ∈ Р , если f( )=0. Другими словами, число является корнем многочлена f(x), если в выражение

+ =0

мы подставим , тогда получим

+ =0.

Таким образом, при подстановке вместо число получается верное выражение. Это означает, что число является корнем равенства f(x)=0.

Поэтому корень многочлена f(x) и корень соответствующего уравнения f(x)=0 по сути одно и то же.

К примеру, найдём корень многочлена f(x)=3 -10+3

Данное выражение является квадратным поэтому для нахождения корня многочлена нам необходимо решить следующее уравнение

3 -10х+3=0.

Для этого необходимо рассмотреть алгоритм решения квадратных уравнений.

Источник

Схема Горнера. Корни многочлена

Разделы: Математика

Цели урока:

Оборудование: карточки для работы в группах, плакат со схемой Горнера.

Метод обучения: лекция, рассказ, объяснение, выполнение тренировочных упражнений.

Форма контроля: проверка задач самостоятельного решения, самостоятельная работа.

Ход урока

1. Организационный момент

2. Актуализация знаний учащихся

— Какая теорема позволяет определить, является ли число корнем данного уравнения (сформулировать теорему)?

Теорема Безу. Остаток от деления многочлена Р(х) на двучлен х-с равен Р(с), число с называют корнем многочлена Р(х), если Р(с)=0. Теорема позволяет, не выполняя операцию деления, определить, является ли данное число корнем многочлена.

— Какие утверждения облегчают поиск корней?

а) Если старший коэффициент многочлена равен единице, то корни многочлена следует искать среди делителей свободного члена.

б) Если сумма коэффициентов многочлена равна 0, то один из корней равен 1.

г) Если все коэффициенты положительны, то корнями многочлена являются отрицательные числа.

д) Многочлен нечетной степени имеет хотя бы один действительный корень.

3. Изучение нового материала

При решении целых алгебраических уравнений приходиться находить значения корней многочленов. Эту операцию можно существенно упростить, если проводить вычисления по специальному алгоритму, называемому схемой Горнера. Эта схема названа в честь английского ученого Уильяма Джорджа Горнера. Схема Горнера это алгоритм для вычисления частного и остатка от деления многочлена Р(х) на х-с. Кратко, как он устроен.

Источник

Корни многочлена. Теорема Безу

Федеральное агентство по образованию

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

Хакасский Государственный Университет

Имени Н. Ф. Катанова

Кафедра математики и методики преподавания математики

Корни многочлена. Теорема Безу

Студенты 1 курса группы ИМ-11

Шабунин Дмитрий Олегович

Зорин Александр Сергеевич

Бобылева Оксана Владимировна

1.2.Определение корня многочлена……………………………………………….4

1.4.Нахождение корней по схеме Горнера. Виды корней……………………….7

2. Этьен Безу. Биография. Теорема Безу. Следствия из теоремы……………….13

2.3 Следствия из теоремы Безу…………………………………………………..14

2.4. Примеры использования теоремы…………………………………………..14

Список используемых источников………………………………………………..17

Тема данного реферата: «Корни многочлена. Теорема Безу».

В нем мы хотим рассмотреть, что такое многочлен, что является корнем многочлена, а также рассказать про схему Горнера и теорему Безу.

В первой части мы разберем понятие многочлена, его корней и их виды и про схему Горнера. Во второй про теорему Безу.

Данная тема довольно актуальна, поскольку теорема Безу является одной из базовых теорем алгебры.

1.1. Понятие многочлена

Многочлен (полином) от одной переменной x – это выражение вида

,

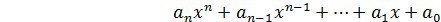
2 члена называются подобными, если их степени равны. При этом подобные между собой члены можно преобразовать в один, т.е. привести подобные члены.

Степенью многочлена называют наибольшую среди степеней многочлена, при этом многочлен f(x)- не тождественный нуль. Обозначается эта степень deg(f).

-многочлен четвертой степени (старшая степень равна четырем);

— многочлен второй степени или квадратный (старшая степень равна двум).

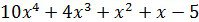
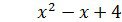
При этом тождественный нуль степени не имеет.

Предполагается, что коэффициенты многочлена принадлежат определенному полю (полю действительных, рациональных, комплексных чисел). Так, если выполнять над многочленом операции сложения, умножения или вычитания при помощи сочетательного, переместительного и распределительных законов, мы получаем снова многочлен.

Из вышесказанного следует, что совокупность всех многочленов с коэффициентами из данного поля Р образует кольцо Р 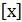— кольцо многочленов над данным полем, это кольцо не имеет делителей нуля, т.е. произведение многочленов, не равных нулю, не может дать нуль.

1.2. Определение корня многочлена

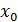
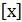
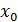
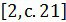
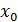
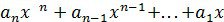
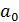
Элемент кольца Р называется корнем многочлена f(x) ∈ Р, если f()=0. Другими словами, число является корнем многочлена f(x), если в выражение

+ =0

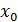
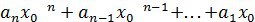
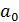
мы подставим , тогда получим

+ =0.

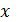
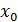
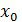
Таким образом, при подстановке вместо число получается верное выражение. Это означает, что число является корнем равенства f(x)=0.

Поэтому корень многочлена f(x) и корень соответствующего уравнения f(x)=0 по сути одно и то же.

К примеру, найдём корень многочлена f(x)=3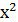-10+3

Данное выражение является квадратным поэтому для нахождения корня многочлена нам необходимо решить следующее уравнение

3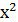-10х+3=0.

Для этого необходимо рассмотреть алгоритм решения квадратных уравнений.

Алгоритм решения квадратных уравнений

+bx+c=0

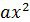
1.Найти дискриминант D по формуле D=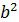-4ac.

2.Если D 0, то уравнение имеет два корня:

, .

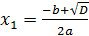
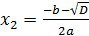
Теперь приступим к решению нашего уравнения 3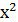-10х+3=0,

где 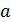=3, b=-10 а с=3.

D=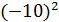-4*3*3=64

Поскольку D>0, то у данного уравнения два корня. Находим их:

; .

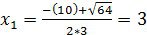
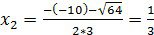
Таким образом, корнями многочлена f(x)=3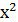-10+3 будут являться числа 3 и .

Схема Горнера (или правило Горнера, метод Горнера) — алгоритм вычисления значения многочлена, записанного в виде суммы полиномов (одночленов), при заданном значении переменной. Она, в свою очередь, и помогает нам выяснить, является ли число 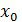корнем данного многочлена или нет.

Для начала рассмотрим как делится многочлен f(x )на двучлен g(x).

Это можно записать следующим образом: f(x):g(x)=n(x), где f(x)- делимое, g(x)- делитель а n(x)- частное.

Но в случае, когда f(x) не делится нацело на g(x) имеет место общая запись выражения

.

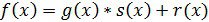
При это степень r(x) 2 // «Городская открытая научно-практическая конференция школьников и студентов». 2007.

7. С. Каплунова Теория многочленов и уравнения высших степеней // Математика: учебно-методическая газета. —2007. — №14. — С.16-17

Источник

В этой статье рассматриваемый многочлен всегда обозначается

СОДЕРЖАНИЕ

Непрерывная зависимость от коэффициентов

Конъюгация

Отсюда следует, что корни многочлена с действительными коэффициентами зеркально симметричны относительно действительной оси.

Это может быть расширено до алгебраического сопряжения : корни многочлена с рациональными коэффициентами сопряжены (то есть инвариантны) относительно действия группы Галуа многочлена. Однако эту симметрию редко можно интерпретировать геометрически.

Границы всех корней

Верхние границы абсолютных значений полиномиальных корней широко используются для алгоритмов поиска корней либо для ограничения областей, в которых следует искать корни, либо для вычисления вычислительной сложности этих алгоритмов.

Было дано много таких оценок, и более точная, как правило, зависит от конкретной последовательности рассматриваемых коэффициентов. Большинство оценок больше или равны единице и, таким образом, не являются точными для многочлена, у которого только корни абсолютных значений меньше единицы. Однако такие многочлены очень редки, как показано ниже.

Оценки Лагранжа и Коши

Лагранж и Коши были первыми, кто оценил сверху все комплексные корни. Граница Лагранжа

Оценка Лагранжа точнее (меньше), чем оценка Коши, только когда 1 больше суммы всех, кроме наибольшего. На практике это относительно редко и объясняет, почему оценка Коши более широко используется, чем оценка Лагранжа. | а я а п | <\ displaystyle \ left | <\ frac > >> \ right |>

что является границей Лагранжа, когда есть хотя бы один корень с абсолютной величиной больше 1. В противном случае 1 является границей корней и не больше границы Лагранжа.

Решение в | z | граница Коши получается, если корень с абсолютным значением больше 1. В противном случае граница также верна, поскольку граница Коши больше 1.

для оценок Лагранжа и Коши соответственно.

Эта оценка инвариантна при масштабировании.

Лагранж улучшил эту последнюю оценку до суммы двух наибольших значений (возможно, равных) в последовательности

Лагранж предоставил также оценку

где обозначает i- й ненулевой коэффициент, когда члены многочленов отсортированы по возрастанию степеней. а я <\ displaystyle a_ >

Используя неравенство Гёльдера

для любого действительного числа h ≥ 1 и

При k = 1 и k = ∞ получаются оценки Коши и Лагранжа соответственно.

При h = k = 1/2 справедлива оценка

Это не только граница абсолютных значений корней, но также граница произведения их абсолютных значений больше 1; см. § неравенство Ландау ниже.

мы должны доказать, что каждый корень z из p удовлетворяет

Записывая уравнение как

В случае 1 формула суммирования геометрической прогрессии дает

Таким образом, во всех случаях

что завершает доказательство.

Другие границы

Было дано много других верхних оценок величин всех корней.

немного улучшает приведенную выше оценку, разделив на два последний аргумент максимума.

где обозначает i- й ненулевой коэффициент, когда члены многочленов отсортированы по возрастанию степеней. Если все коэффициенты отличны от нуля, оценка Фудзивары более точна, поскольку каждый элемент в оценке Фудзивары является средним геометрическим для первых элементов в оценке Кодзимы. а я <\ displaystyle a_ >

Неравенство Ландау

Эта оценка также полезна для ограничения коэффициентов делителя многочлена с целыми коэффициентами: если

Диски, содержащие корни

Из теоремы Руше

Теорема Руше позволяет определять диски с центром в нуле, содержащие заданное количество корней. Точнее, если существует положительное действительное число R и целое число 0 ≤ k ≤ n такие, что

Приведенный выше результат может быть применен, если многочлен

Из теоремы Гершгорина о круге

Если точки интерполяции близки к корням корней многочлена, радиусы дисков малы, и это ключевой компонент метода Дюрана – Кернера для вычисления корней многочлена.

Границы настоящих корней

Ясно, что каждая оценка всех корней применима также и к действительным корням. Но в некоторых случаях полезны более жесткие границы реальных корней. Например, эффективность метода непрерывных дробей для выделения действительных корней сильно зависит от точности оценки положительных корней. Это привело к установлению новых границ, более жестких, чем общие границы всех корней. Эти границы обычно выражаются не только через абсолютные значения коэффициентов, но и через их знаки.

Другие ограничения применимы только к многочленам, все корни которых являются действительными (см. Ниже).

Границы положительных реальных корней

Чтобы дать оценку положительных корней, можно предположить без ограничения общности, поскольку изменение знаков всех коэффициентов не меняет корни. 0>»> а п > 0 <\ displaystyle a_ > 0> 0>»>

Каждая верхняя граница положительных корней

также является оценкой действительных нулей

Применительно к оценке Коши это дает верхнюю оценку

Аналогично, другая верхняя граница положительных корней равна

Если все ненулевые коэффициенты имеют один и тот же знак, положительного корня нет, и максимум должен быть определен как равный нулю.

Многочлены, все корни которых действительны

Отделение корней

Корень разделения многочлена является минимальным расстоянием между двумя корнями, то есть минимальное значение абсолютных значений разности двух корней:

Разделение корня является фундаментальным параметром вычислительной сложности из алгоритмов корневых ознакомительные для полиномов. Фактически, разделение корней определяет точность представления чисел, которая необходима для уверенности в различении разных корней. Кроме того, для изоляции реального корня он позволяет ограничить количество делений интервала, необходимых для изоляции всех корней.

Граница разделения Миньотта составляет

Для многочлена без квадратов с целыми коэффициентами отсюда следует

Теорема Гаусса – Лукаса

Теорема Гаусса – Лукаса утверждает, что выпуклая оболочка корней многочлена содержит корни производной многочлена.

Иногда полезное следствие состоит в том, что если все корни многочлена имеют положительную действительную часть, то также и корни всех производных многочлена.

Статистическое распределение корней

Если коэффициенты гауссово распределение со средним значением нуль и дисперсией из сг затем средней плотности действительных корней дается формулой Каца

Настоящие корни

При больших n средняя плотность вещественных корней около x асимптотически равна

Отсюда следует, что ожидаемое количество действительных корней составляет, используя нотацию большого O

Источник