что такое координатные углы как они нумеруются
Прямоугольная система координат
Содержание
Иногда в жизни, чтобы найти на плоскости какой-то объект, его описывают двумя значениями. Так каждое место в зале кинотеатра имеет два параметра: ряд и место. Каждая клетка на шахматной доске или при игре в «морской бой» описывается номером строки и буквой, обозначающей столбец.
В математике определение местоположения объекта на плоскости придумали быстро находить с помощью системы координат, образованной двумя прямыми, называемых координатными осями (или осями координат).

Абсцисса, ордината, начало координат и единичный отрезок
Оси пересекаются под прямым углом перпендикулярно друг к другу, поэтому такая система координат и называется прямоугольной.
На каждой оси выбирается единичный отрезок, с помощью которого вычисляются координаты объекта. Длиной единичного отрезка может выступать любая единица измерения, но она должна быть одинаковой на каждой из осей. То есть, если единичный отрезок на оси абсцисс задан, например, равным 1 см, то и на оси ординат единичный отрезок тоже должен быть равен одному сантиметру.

Положительное и отрицательное направление
У осей стрелкой задается положительное направление:
Таким образом, все вместе:
образуют в математике прямоугольную систему координат, плоскость называют координатной.
Или другими словами:
Четверти
Осями координат плоскость делится на 4 части, их обозначают римскими цифрами. Каждая часть называется «квадрант». Другие названия: «координатный угол» или «четверть». Нумерация четвертей принята против часовой стрелки в том порядке, в котором указано на рисунке ниже.

Немного из истории
В латинском языке слово «координаты» получилось из двух других: co – «совместно» и ordinatus – «определенный», «упорядоченный».
Впервые необходимость нахождения координат объектов возникла в географии и астрономии. Для этого использовали широту и долготу, определяющие расположение точки на небесной сфере или на поверхности земного шара. Таким образом начали вычислять координаты точек еще в 14 веке. Но упорядочил и систематизировал все знания в 17 веке французский математик по имени Рене Декарт. Поэтому прямоугольную систему координат также называют еще и «декартовой».
Координатный угол
Описание разработки
1) развивать у детей пространственные представления и умение ориентироваться на плоскости.
2) расширять математический кругозор учащегося.
Оборудование: Доска с клетчатым фоном, линейка, тетрадь на печатной основе (№1), учебник.
Повторение пройденного во 2 классе.
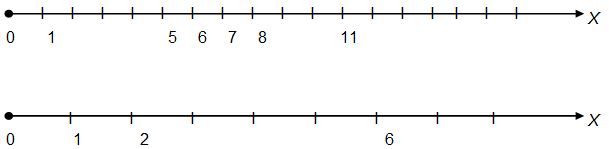
На доске заранее начерчены числовые лучи:
Учитель (У) Что начерчено на доске?
Дети (Д) Числовые лучи. Координатные лучи.
У. Прочитай название луча?
У. Какой буквой обозначено начало луча?
Чем отличаются числовые лучи (1,2) друг от друга?
Д. Единичными отрезками. У луча 1 единичный отрезок равен одной клетке, у луча 2 единичный отрезок равен двум клеткам.
У. Найдите на луче 1 точку А с координатой 3, на луче 2 точку В с координатой 5 и обозначьте их. (Ученики выходят к доске и выполняют задания).
У. Мы с вами вспомнили, как «выглядит» координатный луч. Подумайте, как может на чертеже «выглядеть» координатный угол?
Д. Это два числовых луча, исходящих из одной точки в виде угла.
III. Сообщение темы.
У. Тема урока: « Координатный угол»
IV. Подготовительный этап к восприятию нового материала.
У. Откройте учебник на с.16. Рассмотрите рисунок и ответьте на следующие вопросы:
— Между кем из зрителей сидит Заяц?
— Кто сидит правее места Зайца?
— Кто левее места Волка?
(Дети дают ответы на вопросы)
У. Какие билеты у Удава, Мартышки, Жирафа, Ежа, Льва?
Давайте договоримся, ребята, что при ответе на эти вопросы, вы сначала будете называть место зрителя, а затем ряд, в котором он сидит.
(Дети отвечают на поставленные вопросы)
У. Для того, чтобы точно описать расположение какого-нибудь предмета указывают его координаты на координатной сетке (координатном угле).
Сетку (угол) строят так (Учитель выполняет все построение на клетчатом фоне доски):
Выбирают точку О – (начало координат). Из нее проводят два взаимно перпендикулярных числовых луча – Ох и Оу. Эти лучи называют осями координат, и они образуют координатный угол. Единичный отрезок на каждой из осей должен быть одной и той же длины. Пусть наш единичный отрезок будет равен 1 клетке.
(Далее на координатной сетке учитель указывает точки В и С, а дети пробуют определить их координаты – В (4;0), С (0;4). Учитель обращает внимание детей на то, что переставлять координаты точки нельзя).
VI. Закрепление первичных знаний.
(Работа по учебнику (с. 17) и по тетради «Математика» № 1 («35, 36».))
VII. Повторение пройденного (самостоятельная работа)
Работа в тетради №1, с 13
№38 – решение уравнения с переменной на первом месте
№37 – заполнение таблицы. Задание на нахождение периметра и площади прямоугольника по известным сторонам, нахождение сторон прямоугольника по известным периметру и площади.
У. Что нового вы сегодня узнали на уроке?
Д. Познакомились с координатной сеткой, узнали из чего состоит координатный угол. Учились давать точкам координаты.
VIII. Домашнее задание.
( по учебнику и по тетради «Математика» № 1)
Конспект урока (по ФГОС ) по математике на тему: «Координатный угол»
Ищем педагогов в команду «Инфоурок»
Начальная школа ХХ I века 4 класс.
Тема урока: Координатный угол
Научить детей строить точки с указанными координатами, читать и записывать обозначения вида: А(2; З).
научить детей строить координатную сетку;
вести термины: «начало координат», «оси координат», «координатный угол»,
подготовить учащихся к изучению в старших классах более сложного понятия «координатная
закрепить умения выполнять вычисления в случаях вида: 123+123, 16+12
Развивать внимание, глазомер;
развивать у детей пространственные представления и умения ориентироваться на плоскости;
развивать математическую речь
воспитывать аккуратность, самостоятельность
В.Н. Рудницкая, Т.В.Юдачёва Учебник для учащихся 4 класса Первая часть
М.: «Вентана-Граф», 2010;
В.Н. Рудницкая, Т.В.Юдачёва Математика: 4 класс: рабочая тетрадь № 1
М.: «Вентана-Граф», 2010;
В.Н. Рудницкая, Т.В.Юдачёва Математика: 4 класс: методика обучения
М.: «Вентана-Граф», 2010;
Зеленихина О.В. Математика. 4 класс. Волгоград:Учитель-АСТ, 2005.-112с.
Оборудование урока для учителя:
Интерактивная доска, цветной маркер, мел, учебник, рабочая тетрадь №1, методичка,
Оборудование урока для учащихся:
учебник, рабочая тетрадь № 1, тетрадь в клеточку, простой карандаш, линейку, резинку, ручку.
План урока с указанием времени по этапам:
Проверка выполнения домашнего задания
Подготовка к активной познавательной деятельности
Сообщение темы и цели урока
Усвоение новых знаний
Первичная проверка понимания новых знаний нового материала и закрепление знаний
Систематизация и обобщение знаний
Итог урока, информация о домашнем задании
Организационное завершение урока
Этапы, учебные задачи и содержание урока
Речь и деятельность учителя
Речь и деятельность учащихся (в том числе возможные варианты ответов).
1. Организационный: подготовка учащихся к работе.
Встали, приготовились к математике.
Прозвенел у нас звонок, начинается урок!
Сегодня на уроке нам понадобится:
Тетрадь № 1, тетрадь маленькая в клеточку, ручка, линейка, карандаш.
Встали ровненько! Молодцы! Тихонечко сели.
2. Проверка выполнения домашнего задания:
Дима, пройди, пожалуйста, посмотри, все ли дети сделали домашнее задание.
Хорошо! У всех я проверю сегодня на продлёнке, а Лейле объясню задачу. Не забудь ко мне подойти, а сейчас посмотрите на доску.
Хорошо! Дима просматривает наличие у детей выполненного д.з. в тетради. Дети показывают выполненные задания.
— Все сделали! Только Лейла не сделала задачу, так как не знает как её решить.
3. Подготовка к активной учебно-познавательной деятельности: подготовка учащихся к деятельности на основном этапе урока (актуализация знаний).
Устный счёт: закрепление выполнять вычисления в случаях вида 123+123, 16+12
Вам нужно решить примеры. В клеточки под ответами подставить соответствующие буквы и прочитать имя одного из героев мультфильма
« Каникулы в Простоквашино».
Дети решают. Подставляют в клеточки свои ответы.
Многие не доделали до конца, а догадались когда решили пример с «П».
4.Сообщение темы и цели урока.
Сегодня на уроке мы узнаем, что такое координатный угол и как его построить.
Откройте маленькую тетрадь и запишите: число, классная работа, зелёной пастой тему урока. Спишите с доски без ошибок.
Дети оформляют тетрадь. Записывают:
21.10. Классная работа.
5. Усвоение новых знаний: формирование у учащихся конкретных представлений об изучаемых фактах, понятиях, явлениях, их сущности и взаимосвязях
Для того, чтоб лучше понять, что такое координатный угол, давайте построим числовой луч и отметим на нём точку по координате.
Давайте построим луч Ох.
Учитель показывает заранее построенный луч на интерактивной доске и комментирует.
Одному сантиметру будет равен единичный отрезок, отмечу на числовом луче 6 единичных отрезков.
А(4) – ТОЧКА С КООРДИНАТОЙ 4.
Откройте учебник на стр. 61. Прочитайте задание № 266.
Где находится удав?
Где находится мартышка?
Правильно, можно назвать, конечно, сначала ряд, в котором сидит зритель, а затем его место, так обычно и говорят. Но мы с Вами будем сначала называть место зрителя, а затем ряд, в котором он сидит. Так, например, у Лисы место 4, ряд 2.
Какое место и какой ряд указаны на билете зайца?
Какое место и какой ряд указаны на билете волка?
Прочитайте вопрос над рисунком и ответьте.
Дети строят луч под руководством учителя.
Алина читает задание.
— У льва место 6, ряд 2.
-У зайца место 6, ряд 4.
— У волка 5 место, 2 ряд.
Дети читают вопрос и отвечают.
-Заяц между белкой и ежом.
— Волк между лисой и львом.
Учитель включает физкультминутку «Ёлочка», дети повторяют движения под музыку.
Дети встают и выполняют под музыку физкультминутку, повторяют движения ёлочки, подпевают.
7. Первичная проверка понимания учащимися нового материала и закрепление знаний.
Установление осознанности освоения нового материала и организация деятельности учащихся по применению новых знаний.
Сейчас нам в тетради нужно будет построить координатный угол. Давайте сначала прочитаем, что же это такое. Учебник, страница 62.
Дима, прочитай громко, чётко, не торопясь.
Теперь мы построим координатный угол в тетради.
Учитель на доске показывает.
Пропустите вниз 7-8 см.
Отмечаю точку О ( начало отсчёта) и провожу две оси Ох и Оу, образующие прямой угол.
Посмотрите, у Вас тоже в учебнике взята за единичный отрезок одна клеточка. Сделайте как в учебнике, сверьте, всё ли Вы правильно сделали.
Учитель проходит по классу и проверяет, чтоб дети правильно выбрали единичный отрезок.
Дети читают текст на страничке.
Дети начинают чертить в тетради.
Пропустили вниз место.
Отмечают точку О, проводят две оси Ох и Оу, подписывают х, у.
Сверяют свои записи с учебником, исправляют.
8. Систематизация и обобщение знаний: обеспечение усвоения системы знаний
Поработаем с рисунком нижней части учебника.
Найдите, пожалуйста, точку А.
Начертим координатный угол в тетради, пропустив вниз 6 см.
Запишу на доске А(2;4), такая запись читается так:
Точка Ас координатами два, четыре.
Так как первая координата-число 2, то на оси ОХ
находим число 2; вторая координата- число 4;
В этом же координатном углу отметьте сами точку с координатами 4;2. Назовите, например, её точкой В.
Валя, подойди к доске и отметь эту точку.
Дети, послушайте, какой вывод можно сделать:
Координаты точки представляют пару чисел, переставлять которые нельзя: точки А (2;4) и В (4;2) не совпадают, они расположены в разных местах координатной сетки.
По очереди называем сейчас точки и их координаты, глядя на рисунок нижней части с.62 учебника.
№ 267 выполним устно. Называем точки и их координаты, т.е. пары чисел.
Дети смотрят в учебник.
Дети пропускают 6 см вниз и чертям координатный угол в тетради, слушая объяснение учителя.
Записывают: А (2;4).Вместе с учителем находят точку.
Дети находят эту точку у себя в тетради и сверяют с доской.
Валя находит эту точку на доске в координатном углу.
Дети слушают вывод.
Дети называют координаты точек:
К(3;0), Е(9;0), С (6;1), Х(5;5), М(0;6), Y (8;8), D (0;3)
1). Дети называют точки:
А: два,семь ; В: шесть, семь; С: шесть, три; D : два, три.
2) М: один, ноль; К: четыре, семь; Е: семь, четыре.
9. Итог урока, информация о домашнем задании и рекомендации по его выполнению.
Что нового сегодня узнали на уроке?
Что научились строить?
— Какие задания для Вас оказались сложными?
-Сегодня на уроке активно работали и правильно отвечали: Алина, Валя, Федя, старался Сергей.
Анар успевал за классом, всё записывал в тетрадь. Молодцы!
Посмотрите на № 268, этот номер Вам предстоит выполнить дома. Если Вы прочитаете буквы в том порядке, в котором указаны координаты, то получится красивое слово. Запишите № 268 в дневнике- это 1 номер вы сделаете устно, 2 номера будет по большой тетради-№ 109, 110.
Откройте большую тетрадь и посмотрите на задание № 109, справа записаны точки, рядом Вам надо будет записать их координаты, а в № 110 отметить точки в координатном углу, не забудьте их назвать.
Кому не понятно домашнее задание?
— Мы узнали, что такое координатный угол, как его построить, как нужно находить точку и записывать её координаты.
Дети слушают кого похвалит учитель.
Смотрят на № 268, некоторые дети пытаются прочитать сразу.
Записывают в дневник: № 268 (у), б.т. № 109, 110
Открывают большую тетрадь и слушают рекомендации учителя.
10. Организационное завершение урока
Урок окончен. Приготовьтесь к следующему уроку.
Дети убирают учебные принадлежности, готовятся к следующему уроку, выходят из класса на перемену.
Оформление записей в тетради учащегося.
Задачи урока определены правильно;
Все задачи реализованы;
Содержание урока соответствовало требованиям ФГОС, программе, теме, поставленным задачам, а также уровню развития и особенностям детей.
На уроке использовалась интерактивная доска, что позволило учителю заблаговременно подготовиться к уроку (подготовить материал для устного счёта, начертить ровно координатный угол по клеточкам), что способствовало лучшему восприятию учебного материала. Обучающие видели образец координатного угла, понимали, как найти точку с координатами. Всё это позволило наиболее полно решить образовательные задачи урока.
На уроке удалось выдержать запланированную структуру, всё было выполнено.
Деятельность на 1 и 2 этапе урока у детей сформирована до автоматизма, учитель данный метод использует постоянно;
3 этап был полностью выполнен детьми самостоятельно. Так как данный вид работы используется часто, у детей задание не вызвало затруднений.
На 4 этапе урока дети сами смогли без вопросов записать число, классная работа, тему урока и были готовы слушать учителя дальше;
на 5 этапе урока дети сами смогли построить луч, обозначить точку, активно работали по учебнику, было много хоровых ответов.
Физкультминутку дети с удовольствием самостоятельно и активно провели под музыку.
На 7 этапе прочитали сами, что такое координатный угол и некоторые сильные ученики начертили координатный угол сами, другие внимательно слушали учителя.
8 этап урока оказался для учащихся более сложным, так как впервые им приходилось находить точки на координатных осях и искать их пересечение. Этот этап урока оказался самым длительным по времени.
Учителю пришлось пройти по классу и проконтролировать правильность нахождения точки в координатном углу.
Дети, которые играли когда-то уже в игру «Морской бой» очень обрадовались такой теме урока, оживились и с лёгкостью выполняли последующие задания.
В последнем задании ( назвать точки и их координаты) многие дети допустили ошибки.
На подведении итогов дети ждали, что учитель назовёт именно его и внимательно слушали, но при объяснении домашнего задания дети стали отвлекаться, пришлось потратить много времени для сбора детей, чтоб продолжить объяснение. Возможно, дети утомились и хотели уйти на перемену.
Последний этап прошёл быстро. Дети сами стали всё убирать. Готовиться к следующему уроку, выходить из класса.
На уроке применялись приёмы активизации познавательной деятельности
учеников. Давались разнообразные задания, что способствовало преодолению природной пассивности и активному включению в учебный процесс. А так же использовалось задание на сравнение, что помогло лучше освоить и запомнить учебный материал.
На этапе усвоения новых знаний продолжалось формирование ведущих идей и понятий курса. Ученики в процессе объяснения учились по рисунку в учебнике определять места животных, что способствовало плавному переходу к изучению темы, начертили луч.
Такой подход позволил существенно повысить уровень математического
образования школьников, развить их мышление и воспитать устойчивый
интерес к занятиям математикой.
Закрепление было организовано на поисковом уровне.
Объём и характер домашнего задания соответствовал возрастным особенностям младших школьников.