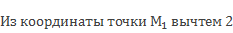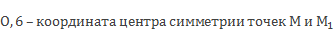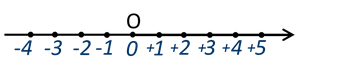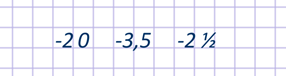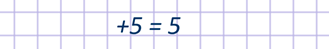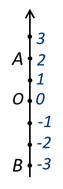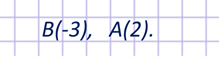что такое координатная прямая 6 класс
Что такое координатная прямая 6 класс
Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту
В этом уроке Вы узнаете, что такое координатная прямая, научитесь на ней обозначать положительные и отрицательные числа, определять координаты симметричных точек.
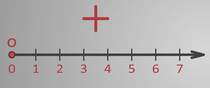
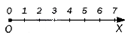
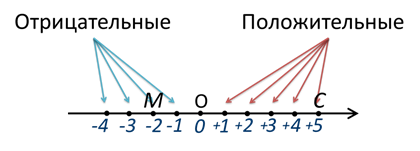
Давайте возьмем координатный луч.
На нем отмечено начало – точка О, единичный отрезок и справа от начала координат у нас находятся положительные числа в порядке возрастания.
А где расположить отрицательные?
Чтобы отметить отрицательные числа нужно луч дополнить противоположным ему лучом и нанести на него такие же деления.
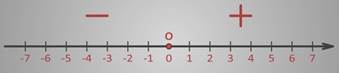
Таким образом, получилась координатная прямая.
Справа от точки О – начала координат – находятся положительные числа, а слева – отрицательные.
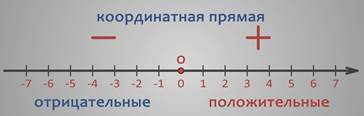
Следовательно, координатная прямая – это прямая с указанным на ней началом отсчета, направлением отсчета и единичным отрезком.
Координата – число, показывающее положение точки на координатной прямой.
Числа, расположенные справа от точки О на координатной прямой – положительные, соответственно направление, в котором они расположены называют положительным.
Числа, которые расположены слева – отрицательные, поэтому направление, в котором они расположены называется отрицательным.
На координатной прямой стрелкой указывается только положительное направление. Число 0 разделяет положительные и отрицательные числа.
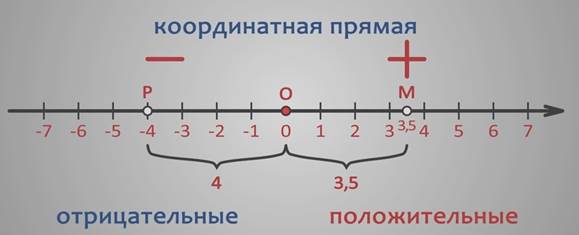
Каждому числу соответствует единственная точка прямой.
Например, числу 3,5 соответствует точка М, которая удалена от начала отсчета, т. е. от точки О, на расстояние, равное 3,5 (в заданном масштабе), и отложена от точки О в заданном (положительном) направлении.
Верно и обратное: каждая точка координатной прямой соответствует единственному числу.
В таких случаях соответственно говорят «ось x», «ось y» или «ось t».
Координатные прямые могут располагаться на плоскости по-разному, не только горизонтально.
Например, шкалу на термометре можно назвать координатной прямой.
Она будет вертикальной.
В этом случае положительные числа будут находиться выше 0, а отрицательные ниже 0.
Выполним практическое задание:
Изобразим координатную прямую.
Для этого начертим прямую, отметим на ней начало координат – точку О, выберем единичный отрезок, нанесем деления справа и слева от 0, покажем стрелкой направление отсчета, назовем координатную прямую «осью х».
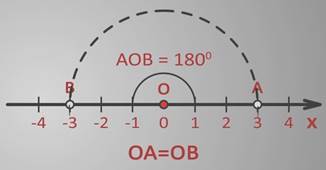
Отметим на координатной прямой точки А (3), В (-3).
Обратите внимание: расстояние от точки А до начала координат точки О будет равно расстоянию OB.
точки А и В будут центрально-симметричны относительно начала отсчета координатной прямой точки О (0).
Следует отметить, что центром симметрии точек на координатной прямой может быть любая точка данной прямой.
Поучимся находить симметричные точки на координатной прямой.
Пусть точка О (0) – центр симметрии.
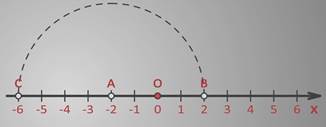
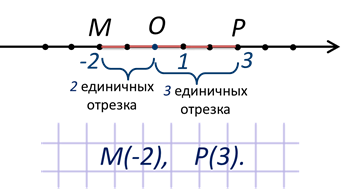
Найдем точку, симметричную точке С (-6).
Такой точкой будет точка расположенная по другую сторону от центра симметрии.
Центром симметрии теперь будет точка А (-2).
Между точками С (-6) и А (-2) – четыре единичных отрезка.
Отсчитаем от точки А (-2) четыре единичных отрезка вправо отметим точку В.
Определим ее координату – (2).
Таким образом, точки С (-6) и В (2) будут центрально-симметричны относительно точки А (-2).
А как определить координату центра симметрии двух точек на координатной прямой?
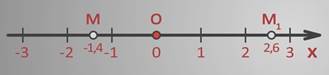
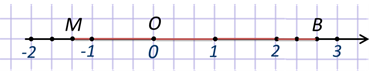
Пусть даны симметричные точки М(-1,4) и М1(2,6).
Расстояние от точки М до О(0) 1,4, от М1 до начала координат – 2,6.
Центр симметрии должен быть посередине.
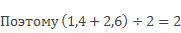
Таким образом, в этом уроке Вы узнали, что такое координатная прямая, научились определять координаты точек и находить симметричные точки.
Урок «Координатная прямая» (6 класс)
Ищем педагогов в команду «Инфоурок»
Описание презентации по отдельным слайдам:
Описание слайда:
Описание слайда:
Работаем устно
1. Убытки компании составили 1000 000 руб., а через несколько лет компания получила прибыль 500 000 руб.
2. Летом средняя температура воздуха 25 ºС тепла, а зимой – 20 ºС мороза.
3. Жёлоб Пуэрто-Рикко (Атлантический океан) имеет глубину 8742 м.
4. Долина смерти находится на 86 м ниже уровня моря и здесь было зафиксировано 57 ºС тепла.
5. По мере восхождения на гору Эльбрус, высота которой 5 642 м над уровнем моря, температура может опуститься до 30 ºС ниже нуля.
6. Долгое время одни числа называли «долг», «недостача», а другие «имущество».
7. Нулевая отметка на шкале градусника.
Распределить информацию в три колонки
Описание слайда:
Описание слайда:
Описание слайда:
Выполним построения
Начертите координатный луч.
Отложите точку А с координатой 3.
Можно ли влево отложить точку удаленную на такое же расстояние?
Какую она будет иметь координату?
Описание слайда:
Координатная прямая
Математика, 6 класс
Обыденнова Н.С.
Описание слайда:
Положительные и отрицательные числа. Координатная прямая
Проведём прямую. Отметим на ней точку 0 (ноль) и примем эту точку за начало отсчёта.
Описание слайда:
Положительные и отрицательные числа. Координатная прямая
Число 0 не является ни положительным, ни отрицательным.
Прямая, на которой отмечено:
• начало отсчёта (точка 0);
• единичный отрезок;
• стрелкой указано положительное направление;
называется координатной прямой или числовой осью.
Каждая точка на координатной прямой имеет свою координату. Координата пишется в круглой скобке.
А(-1), С(2,5), Д(-4,7)
Описание слайда:
Описание слайда:
Домашнее задание
П.30 правила
№ 847, 849
Описание слайда:
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Общая информация
Международная дистанционная олимпиада Осень 2021
Похожие материалы
Урок «Вычитание рациональных чисел» (6 класс)
Технологическая карта урока по математике в 6 классе по теме » Уравнения»
» Рабочая программа 10кл.мат.-2021-2022″
Программа элективного курса по математике 9 класс «Математика: подготовка к ОГЭ».
Конспект урока по математике на тему «Умножение»(6 класс)
Презентация по математике на тему: «Геометрические фигуры» 5 класс
Самостоятельная работа по математике на тему «Решение задач. 3-я четверть» ( 4 класс)
Технологическая карта урока по математике на тему «Смешанные числа. Преобразование неправильной дроби в смешанное число» ( 4 класс)
Не нашли то что искали?
Воспользуйтесь поиском по нашей базе из
5298992 материала.
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
Заболеваемость ковидом среди студентов и преподавателей снизилась на 33%
Время чтения: 4 минуты
Минобрнауки разработало концепцию преподавания истории российского казачества
Время чтения: 1 минута
СК предложил обучать педагогов выявлять деструктивное поведение учащихся
Время чтения: 1 минута
Минпросвещения будет стремиться к унификации школьных учебников в России
Время чтения: 1 минута
Путин попросил привлекать родителей к капремонту школ на всех этапах
Время чтения: 1 минута
В российских школах оборудуют кабинеты для сообщества «Большой перемены»
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Координатная прямая (числовая прямая), координатный луч
Координатный луч изображается по той же схеме, но существенно отличается. Мы ставим точку отсчета и отмеряем единичный отрезок.
Данная статья посвящена разбору таких понятий, как координатный луч и координатная прямая. Мы остановимся на каждом понятии и подробно рассмотрим примеры. Благодаря этой статье вы сможете освежить свои знания или ознакомиться с темой без помощи преподавателя.
Координатный луч
Для того, чтобы определить понятие координатного луча, следует иметь представление о том, что такое луч.
На примере мы видим, что O является началом луча.
Координатный луч изображается по той же схеме, но существенно отличается. Мы ставим точку отсчета и отмеряем единичный отрезок.
От конца единичного отрезка нужно отложить несколько штрихов и сделать разметку.
Координатный луч – это шкала, которая может длиться до бесконечности.
Мы в любом случае сможем продолжить шкалу до того числа, которое нам необходимо. Вы можете записывать числа как удобно – под лучом или над ним.
Для отображений координат луча могут использоваться как заглавные, как и строчные буквы.
Координатная прямая
Проведите луч в противоположную сторону, дополнив его до прямой
Отложите единичные отрезки по примеру, указанному выше
Вы можете отметить только начало отсчета и единичные отрезки. Смотрите на примере, как это будет выглядеть.
Соответствие между точками координатной прямой и действительными числами
Координатная прямая может содержать множество точек. Они напрямую связаны с действительными числами. Это можно определить, как взаимно однозначное соответствие.
Каждой точке на координатной прямой соответствует единственное действительное число, а каждому действительному числу соответствует единственная точка на координатной прямой.
Для того, чтобы лучше понять правило, следует отметить точку на координатной прямой и посмотреть, какое натуральное число соответствует отметке. Если эта точка совпадает с началом отсчета, она будет отмечена нулем. Если точка не совпадает с началом отсчета, мы откладываем нужное количество единичных отрезков до тех пор, пока не достигнем указанной отметки. Число, записанное под ней, и будет соответствовать данной точке. На примере, указанном внизу, мы покажем вам это правило наглядно.
Если мы не можем найти точку, откладывая единичные отрезки, следует отмечать также точки, составляющие одну десятую, сотую или тысячную долю единичного отрезка. На примере можно подробно рассмотреть данное правило.
Отложив несколько подобных отрезков, мы сможем получить не только целое, но и дробное число – как положительное, так и отрицательное.
Множество действительных чисел включается в себя все числа, которые можно записать в виде дроби. Это позволяет выявить правило.
Каждой точке координатной прямой соответствует конкретное действительное число. Разные точки определяют разные действительные числа.
Это соответствие однозначно –каждой точке соответствует определенное действительное число. Но это работает также и в обратном направлении. Мы также можем указать определенную точку на координатной прямой, которая будет относиться конкретному действительному числу. Если число не является целым, то нам необходимо отметить несколько единичных отрезков, а также десятых, сотых долей в заданном направлении. Например, числу 400350 отвечает точка на координатной прямой, в которую из начала отсчета можно попасть, отложив в положительном направлении 400 единичных отрезков, 3 отрезка, составляющих десятую долю единичного, и 5 отрезков – тысячную долю.
Каждой точке на координатной прямой отвечает действительное число, и каждое действительное число отмечается в виде точки на координатной прямой.
Благодаря этому утверждению координатную прямую зачастую определяют как числовую.
Координаты точек на координатной прямой
Число, соответствующее точке на координатной прямой, называется координатой этой точки.
Ранее было отмечено, что к каждому числу относится единственная точка на прямой. Можно сказать, что координата точки определяет ее положение на прямой. Именно координата задает эту точку.
Урок 27 Бесплатно Координаты на прямой
В этом уроке мы познакомимся с положительными и отрицательными числами, поймем, к чему относится нуль.
Не забудем рассказать также про неположительные и неотрицательные числа, а после этого узнаем, что такое координатная прямая и из чего она состоит.
Положительные и отрицательные числа
Начнем с сухих, но емких определений.
Обычно + не пишется, а просто подразумевается.
Мы могли бы их записать и со знаком «+»:
В таком случае нужно читать запись буквально: «плюс два», «плюс одна вторая» и так далее.
Такая запись добавляет громоздкости записи, и обычно все- таки «+» опускают.
Приведем примеры отрицательных чисел:
-3, \(\mathbf<-\frac<1><6>>\), \(\mathbf<-32\frac<4><5>>\), -784285332
Читать в данном случае также нужно дословно: «минус три», «минус одна шестая» и так далее.
Минус уже опустить нельзя, так как тогда получится, что число положительное.
Важные факты:
Если нам надо сравнить два числа, одно из которых положительное, а другое отрицательное, то можно смело утверждать, что число, которое положительно, больше числа, которое отрицательно.
Если надо сравнить число с нулем, то достаточно понять, положительное оно или отрицательное. Если положительное, значит, больше нуля, если же отрицательное, то меньше нуля.
Более подробно про сравнение чисел мы поговорим в следующих уроках, а пока потренируемся отличать положительные и отрицательные числа.
Пройти тест и получить оценку можно после входа или регистрации
Неположительные и неотрицательные числа
Иногда необходимо обозначить множество чисел, больших или равных нулю, или же наоборот, меньших или равных нулю.
Удобно, что для этого есть специальные определения.
Соответственно, если мы хотим привести примеры неотрицательных чисел, то можем привести положительные числа или 0.
Примеры: 0, 1, 956, \(\mathbf<\frac<4><9>>\), \(\mathbf<342\frac<1><9>>\).
В данном случае примерами будут соответственно отрицательные числа или 0.
Если необходимо определить, является ли число неотрицательным или неположительным, то ответить надо следующим образом:
Также отметим важные факты про сравнение неположительных и неотрицательных чисел с нулем:
Пройти тест и получить оценку можно после входа или регистрации
Координатная прямая
Начнем с определения, а потом посмотрим на вариации и примеры координатных прямых в жизни.
Если хотя бы одной из этих трех составляющих нет, то прямая уже не может быть координатной.
Выше мы показали самую простую вариацию координатной прямой.
Но обычно для удобства наносят штрихи по всей длине, чтобы не отмерять единичные отрезки.
Также мы можем подписывать числа не только под точкой начала отсчета и точкой, дающей понимание о длине единичного отрезка, но и под остальными точками тоже.
Если мы не хотим загромождать картинку, то можно отмечать точки с какой-то периодичностью.
Неизменным на всех этих картинках остается наличие трех пунктов из определения:
В жизни координатные прямые, полностью удовлетворяющие нашему определению, могут встречаться довольно редко.
Например, на ртутном термометре подразумевается, что направление совпадает с направлением увеличения чисел на шкале.
На нем же мы видим, что числа стоят не у каждого штриха, а у каждого 5-го или каждого 10-го, так картинка становится более читаемой.
Еще один пример: обычная линейка или рулетка. Тут тоже направление подразумевается, поэтому нельзя однозначно сказать, что это координатная прямая.
На линейке, в отличие от градусника, не часто увидишь отрицательные числа. Действительно, -5 градусов интересуют нас больше, чем -5 сантиметров.
На этом рисунке видно, что у точки начала координат (точка O) координата равна нулю, а у точки (А), дающей информацию о единичном отрезке,
координата- 1.
Чтобы найти координату точки мы должны отсчитать количество единичных отрезков между точкой и точкой начало отсчета. А дальше, если эта точка стоит после точки начала отсчета, то взять количество единичных отрезков. В противном случае, если точка находится перед точкой начала отсчета, то взять количество единичных отрезков со знаком «минус».
Например, чтобы найти координату точки C мы отсчитываем количество отрезков от начала координат; получаем, что их 2, запоминаем это.
Точка С находится справа от точки начала отсчета, или дальше по направлению, чем точка начала отсчета. Значит, берем непосредственно число 2 в качестве координаты.
Между точкой B и точкой начала отсчета 3 единичных отрезка, но если смотреть относительно точки начала отсчета, то она находится левее или раньше по направлению, значит, мы берем количество единичных отрезков со знаком «минус» и координатой точки B будет \(\mathbf<-3>\).
Естественно, единичных отрезков между точкой и точкой начала отрезков может получиться нецелое число.
Точка D идет перед точкой начала отсчета, если смотреть по направлению, а значит, координата должна быть отрицательный.
Таким образом, координата точки D будет равна \(\mathbf<-1.5>\).
Мы не случайно отходим от простых понятий «справа»/«слева», когда говорим о взаимном расположении точек.
Представьте, что направление идет в другую сторону.
Ну и конечно же, прямая может быть вообще расположена вертикально, тогда говорить о направлениях «право»/«лево» вообще не приходится.
Пройти тест и получить оценку можно после входа или регистрации
Координаты на прямой
Урок 27. Математика 6 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Координаты на прямой»
Вам уже известно понятие «координатный луч».
Это луч. Но на нём в отличие от обычного луча есть начало отсчёта, единичный отрезок и стрелка, указывающая положительное направление.
Дополним этот луч до прямой. На новом луче мы тоже можем отложить отрезки, равные единичному.
Чтобы различать друг от друга координаты на этих лучах, договорились перед координатами на одном луче ставить знак «+», а перед координатами на другом луче знак «-».
Числа со знаком «+» называются положительными числами.
Числа со знаком «-» называются отрицательными числами.
Нельзя сказать, что для вас отрицательные числа совсем новые.
Записывают такие числа вот так:
Читают: минус 20; минус 3,5; минус 2 ½.
При записи положительных чисел знак «+» писать не обязательно.
Поэтому вместо плюс 5 пишут 5. То есть +5 и 5 это одно и то же число, только обозначенное по-разному.
Как же быть с числом 0?
На прямой, которую мы изобразили, оно отделяет положительные числа от отрицательных. Отрицательное оно или положительное?
Запомните! Само число 0 не является не отрицательным, ни положительным числом.
Теперь посмотрим на рисунок, который у нас получился:
· на ней выбрано начало отсчёта;
· стрелкой обозначено положительное направление (то есть луч с положительными координатами).
Такая прямая называется координатной прямой.
Точка С имеет координату 5.
Кстати, располагаться координатная прямая может не только горизонтально, но и вертикально.
Теперь давайте вспомним, где нам уже встречалась такая шкала. Где применяются положительные и отрицательные числа?
Термометр за окном может показывать положительную и отрицательную температуру.
Линия времени на уроках истории похожа на координатную прямую.
На ней можно отметить время до нашей эры и время нашей эры.
Найдём координаты точек. Координата характеризует расстояние от данной точки до начала координат, выраженное в единичных отрезках.
Посмотрите, какую запись можно сделать в тетради.
Отметить на координатной прямой точку В с координатой 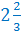
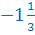
Координатная прямая – это прямая, на которой выбрано начало отсчёта; единичный отрезок. Стрелкой обозначено положительное направление.
Числа, которые мы откладываем левее начала отсчёта, называют отрицательными.
Числа, которые мы откладываем правее начала отсчёта, называют положительными.
Число 0 не является не отрицательным, ни положительным числом.