что такое конкурирующие точки
Что такое конкурирующие точки
Рассмотрим три основных варианта взаимного расположения точек, в зависимости от соотношения координат определяющих их положение в пространстве:
1. Рассмотрим точки А и В (рис.13), все три координаты которых отличаются, их взаимное расположение можно оценить по удаленности к плоскостям проекций:
— YА>YВ. Тогда точка А расположена дальше от плоскости П2 и ближе к наблюдателю, чем точка В;
— ZА>ZВ. Тогда точка А расположена дальше от плоскости П1 и ближе к наблюдателю, чем точка В;
Рисунок 13. Взаимное расположение точек
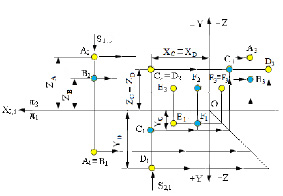
2. На рисунке 14 представлены точки А, В, С, D , у которых одна из координат совпадает, а две другие отличаются, их взаимное расположение можно оценить по удаленности к плоскостям проекций следующим образом:
– ZА=ZВ=ZС, то точки А, В и С равноудалены от плоскости П1 и их фронтальные и профильные проекции расположены, соответственно, на прямых А2 В2//x12 и А 3С 3 // y. Геометрическим местом таких точек служит плоскость, параллельная П1 ;
3. Если у точек равны две одноименные координаты, то они называются конкурирующими . Конкурирующие точки расположены на одной проецирующей прямой. На рис. 14. даны три пары таких точек, у которых:
Рисунок 14. Конкурирующие точки
Соответствующие проекции конкурирующих точек совпадают.
При проецировании на соответствующую плоскость проекций одна точка «закроет» другую точку, конкурирующую с ней, соответствующая проекция которой окажется невидимой.
Определение видимости в начертательной геометрии с примерами
Определение видимости:
Точки, расположенные на одной проецирующей прямой, называются конкурирующими.
Точки, расположенные на одной горизонтально-проецирующей прямой, называются конкурирующими относительно горизонтальной плоскости проекций. Из двух точек A и B (рис. 7.1,а), конкурирующих на горизонтальной проекций, видима та, высота которой больше (B-видима, A-плоскости невидима).
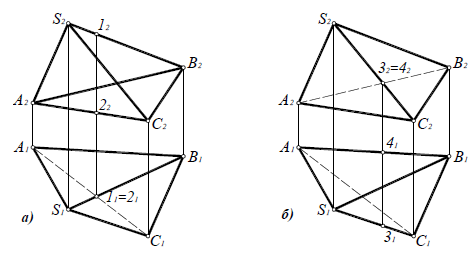
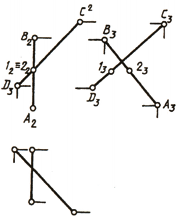
Рассмотрим определение видимости на комплексном чертеже на примере тетраэдра (рис. 7.2).
Для определения видимости на горизонтальной плоскости проекций нужно найти точки, конкурирующие относительно П1 (рис. 7.2,а). Ребра SA, SC, AB и BC являются очерковыми, следовательно, видимыми. Остается выяснить видимость ребер AC и SB. Точки 1 ∈ SB и 2 ∈ACявляются конкурирующими на П1, поскольку находятся на горизонтально-проецирующем луче. Фронтальная проекция точки 1 лежит выше (высота точки 1 больше), поэтому она видима на П1, следовательно, видимо и реброSB, а ребро AC невидимо. Если хотя бы одно ребро грани невидимо, вся грань ABCневидима на П1.
Видимость на фронтальной проекции (рис. 7.2,б) определяется с помощью конкурирующих точек 3 ∈ SCи 4 ∈AB. Горизонтальная проекция точки 3 лежит ниже (глубина точки 3 больше), следовательно, точка 3 и ребро SCна фронтальной плоскости проекции видимы, а точка 4, ребро AB и грань ASB невидимы на П2.
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Научная электронная библиотека
Пиралова О. Ф., Ведякин Ф Ф.,
3.2. Метод конкурирующих точек
Метод конкурирующих точек используется в начертательной геометрии для определения взаимной видимости двух геометрических фигур, с помощью точек, принадлежащих этим фигурам. Рассмотрим пример (рис. 3.1)
Рис. 3.1. Пример изображения конкурирующих точек
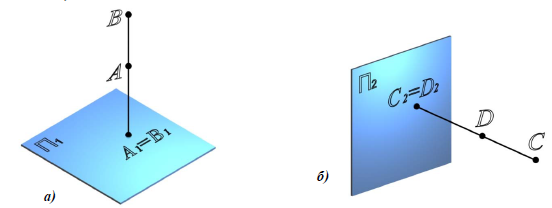
Конкурирующими точками называются такие точки пространства, у которых совпадают какие-либо две одноименные проекции. Конкурирующие точки расположены на одной проецирующей прямой.
На рис. 3.1 показаны две пары конкурирующих точек А и В (совпадают горизонтальные проекции А1 ≡ В1) и C и D (совпадают фронтальные проекции С2 ≡ D2).
Точки А и В находятся на одинаковом расстоянии от фронтальнойπ2 и профильной π3 плоскостей проекций, имеют одинаковые координаты х и у, а координаты z – разные. Значит точки А и В находятся на разных расстояниях от горизонтальной π1 плоскости проекций.
Метод конкурирующих точек заключается в определении взаимной видимости точек (фигур) по их несовпадающим проекциям. При проецировании точек А и В на фронтальную плоскость проекций π2, точка А находится выше точки В относительно плоскости и закроет точку В (считается, что наблюдатель смотрит на плоскости проекций из бесконечности и направление луча зрения параллельно проецирующему лучу S). Значит видна будет точка А, у которой координата z больше, чем у точки В (ZB > ZA).
На плоскости π2 видна точка D, так как она находится ближе к наблюдателю (дальше от плоскости π2, YD>YC) и закрывает невидимую точку С.
На плоскости π3 видна точка Е, так как она находится ближе к наблюдателю (дальше от плоскости π3, XE>XF) и закрывает невидимую точку F.
Методом конкурирующих точек пользуются при определении видимости пересекающихся геометрических фигур.
2.3. Видимость. Конкурирующие точки.
Точки, у которых совпадает одна пара одноименных проекций (а другие проекции не совпадают),
называются конкурирующими точками.
Следствие: две точки, принадлежащие проецирующей прямой, являются конкурирующими точками.
Понятием конкурирующих точек следует пользоваться при решении вопроса о том, какая из двух скрещивающихся прямых проходит выше другой или впереди другой в месте кажущегося пересечения.
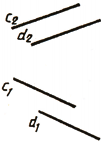
Рассматривая скрещивающиеся прямые c и d (рис. 2.7), устанавливаем, что на фронтальной и горизонтальной проекции видна прямая d.
2.3. Определение натуральной величины отрезка прямой общего положения и углов его наклона к плоскостям проекций.
Настоящая задача является первой из группы метрических задач. Выделяя на рис. 2.9 треугольники ABA 1 и АВВ 1 видим, что в обоих случаях отрезок AВ является гипотенузой этих прямоугольных треугольников.
Любой из этих треугольников мы можем построить на комплексном чертеже, т.к. имеются отрезки, конгруентные катетам этих треугольников (рис. 2.10).
Напомним, что две фигуры называются конгруентными, если одна из них может быть переведена в другую при помощи движения.
Для треугольника АВВ 1 :
Для треугольника ABA 1 :
Приняв проекции отрезка за один из катетов и разность координат концов другой проекции отрезка за второй (рис. 2.10) строим конгруэнтные треугольники.
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
Глава 7. Изображение линий на чертежах
§ 41. Взаимное расположение двух прямых
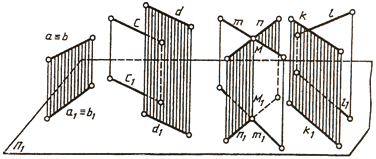
Две прямые пространства могут иметь различное расположение (рис. 74). Они могут совпадать а ≡ b, быть параллельными с ׀׀ d, пересекаться m ∩ n и скрещиваться (k°/l).
Если две прямые параллельны, то на комплексном чертеже (рис. 75, а) их одноименные проекции параллельны.
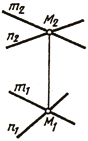
Если две прямые пересекаются в некоторой точке М, то проекции этой точки должны принадлежать одноименным проекциям прямых, т. е. точки пересечения одноименных проекций пересекающихся прямых должны лежать на одной линии связи (рис. 75, б):
Если две прямые скрещиваются, то их одноименные проекции могут пересекаться в точках, не лежащих на одной линии связи (рис. 75, в):
В другом случае одна пара проекций будет пересекаться, а вторая может быть параллельными прямыми (рис. 75, г):
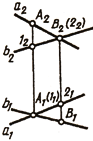
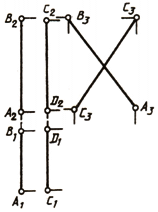
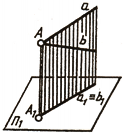
Следует обратить внимание на особые случаи определения взаимного расположения двух прямых в пространстве. Если одна из них (рис. 76, а) или обе (рис. 76, 6) окажутся профильными прямыми, то для определения взаимного расположения их необходимо построить третью, профильную проекцию этих прямых.
Если рассматривать рис. 76, а, можно ошибочно сделать предположение, что прямые АВ и CD пересекаются. Однако если построить профильные проекции этих прямых, станет видно, что они скрещиваются, так как точки 1 и 2 не совпадают, а являются фронтально конкурирующими точками.
Рассматривая рис. 76, б,можно ошибочно предположить, что прямые АВ и CD параллельны. Но после построения их профильных проекций увидим, что они скрещиваются, так как на этой плоскости проекции их пересекаются.
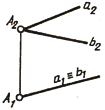
Прямые а и b горизонтально конкурирующие, имеют общую горизонтально проецирующую плоскость (рис. 77, б).


© Красноярский государственный аграрный университет
© Управление информационных технологий
© Кафедра Технологии машиностроения