что такое комплексная плоскость

Комплексная плоскость

Комплексная плоскость — это плоскость с прямоугольной декартовой системой координат xOy.

Комплексные числа на этой плоскости изображаются в виде точек либо в виде векторов.

I. Геометрическая интерпретация комплексных чисел в виде точек на комплексной плоскости

Каждому комплексному числу z=a+bi на комплексной плоскости соответствует точка z(a;b).

И наоборот, каждую точку z(a;b) плоскости можно считать изображением комплексного числа z=a+bi.

Таким образом, геометрическое изображение комплексных чисел в виде точек координатной плоскости устанавливает взаимно однозначное соответствие между комплексными числами и точками плоскости.

Действительные числа z=a+0i на комплексной плоскости изображаются точками с координатами (a;0) (лежащими на оси Ox), чисто мнимые числа z=0+bi — точками с координатами (0;b) (на оси Oy).

Поэтому ось абсцисс Ox называют действительной осью, а ось ординат Oy — мнимой осью.

Комплексно-сопряженные числа на плоскости изображаются точками, симметричными относительно оси Ox; противоположные комплексные числа — точками, симметричными относительно точки O (начала координат).

Комплексную плоскость называют также плоскостью Гаусса.

Геометрическая интерпретация комплексных чисел в виде радиус-векторов

Комплексные числа изображаются также векторами с началом в точке O и концом в точке z(a:b) (радиус-векторами).

Соответствие между комплексными числами и радиус-векторами также является взаимно однозначным.

Геометрически сумма комплексных чисел в виде радиус-векторов строятся по правилу параллелограмма сложения векторов.

Геометрически комплексные числа также можно вычитать, как векторы.

На комплексной плоскости удобно изображать различные множества комплексных чисел, удовлетворяющие заданным условиям.

Источник

В математика, то комплексная плоскость или же z-самолет является геометрическим представлением сложные числа установленный реальная ось и перпендикуляр мнимая ось. Его можно рассматривать как модифицированный Декартова плоскость, с реальная часть комплексного числа, представленного смещением по оси x, и мнимая часть перемещением по оси ординат. [примечание 1]

Комплексную плоскость иногда называют Самолет Арганд или же Самолет Гаусса.

Содержание

Условные обозначения

В комплексный анализ, комплексные числа обычно обозначаются символом z, который можно разделить на его реальные (Икс) и мнимой (у) части:

Например: z = 4 + 5я, куда Икс и у настоящие числа, и я это мнимая единица. В этой привычной записи комплексное число z соответствует точке (Икс, у) в Декартова плоскость.

На декартовой плоскости точка (Икс, у) также могут быть представлены в полярные координаты в качестве

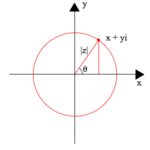
z = Икс + я у = | z | ( потому что ⁡ θ + я грех ⁡ θ ) = | z | е я θ < displaystyle z = x + iy = | z | left ( cos theta + i sin theta right) = | z | e ^ >

и часто думаю о функции ж как преобразование из z-плоскость (с координатами (Икс, у)) в ш-плоскость (с координатами (ты, v)).

Диаграмма Аргана

Диаграмма Аргана относится к геометрическому участок комплексных чисел как точки z = x + iy, используя ось x как действительную ось и ось y как мнимую ось. [3] Такие участки названы в честь Жан-Робер Арган (1768–1822), хотя впервые они были описаны норвежско-датским землемером и математиком. Каспар Вессель (1745–1818). [примечание 4] Диаграммы Аргана часто используются для определения положения нули и полюсы функции на комплексной плоскости.

Стереографические проекции

Может быть полезно думать о комплексной плоскости, как если бы она занимала поверхность сферы. Учитывая сфера единичного радиуса, поместите его центр в начало комплексной плоскости, ориентируя так, чтобы экватор на сфере совпадал с единичным кругом в плоскости, а северный полюс находился «над» плоскостью.

Это не единственная возможная, но правдоподобная стереографическая ситуация проекции сферы на плоскость, состоящую из двух или более значений. Например, северный полюс сферы может быть помещен поверх начала координат. z = −1 в плоскости, касательной к окружности. Детали особого значения не имеют. Любая стереографическая проекция сферы на плоскость создаст одну «точку в бесконечности», и она отобразит линии широты и долготы на сфере в окружности и прямые линии, соответственно, на плоскости.

Режем самолет

При обсуждении функций комплексной переменной часто удобно думать о резать в комплексной плоскости. Эта идея естественно возникает в нескольких различных контекстах.

Многозначные отношения и точки ветвления

Рассмотрим простое двузначное отношение

Прежде чем мы сможем рассматривать эти отношения как однозначные функция, диапазон результирующего значения нужно как-то ограничить. Когда имеешь дело с квадратными корнями из неотрицательных действительных чисел, это легко сделать. Например, мы можем просто определить

у = грамм ( Икс ) = Икс = Икс 1 / 2 < Displaystyle у = г (х) = < sqrt > = х ^ <1>>

быть неотрицательным действительным числом у такой, что у 2 = Икс. Эта идея не так хорошо работает в двумерной комплексной плоскости. Чтобы понять почему, давайте подумаем о том, как ценность ж(z) меняется в зависимости от точки z перемещается по единичному кругу. Мы можем написать

Очевидно, как z движется по кругу, ш очерчивает только половину круга. Таким образом, одно непрерывное движение в комплексной плоскости преобразовало положительный квадратный корень е 0 = 1 в отрицательный квадратный корень е я = −1.

Отрезок ветви в этом примере не обязательно должен лежать вдоль действительной оси. Это даже не обязательно должна быть прямая линия. Любая непрерывная кривая, соединяющая начало координат z = 0 с точкой на бесконечности будет работать. В некоторых случаях отрезок ветви даже не должен проходить через бесконечно удаленную точку. Например, рассмотрим отношения

Эту ситуацию легче всего визуализировать с помощью стереографическая проекция, описанная выше. На сфере один из этих разрезов проходит в продольном направлении через южное полушарие, соединяя точку на экваторе (z = −1) с другой точкой на экваторе (z = 1), и проходя через южный полюс (начало координат, z = 0) в пути. Второй вариант разреза проходит в продольном направлении через северное полушарие и соединяет те же две экваториальные точки, проходя через северный полюс (то есть точку на бесконечности).

Ограничение области определения мероморфных функций

А мероморфная функция сложная функция, которая голоморфный и поэтому аналитический везде в своей области, кроме конечного, или счетно бесконечный, количество баллов. [примечание 5] Точки, в которых такая функция не может быть определена, называются полюса мероморфной функции. Иногда все эти полюса лежат на одной прямой. В этом случае математики могут сказать, что функция «голоморфна на плоскости сечения». Вот простой пример.

Γ ( z ) = е − γ z z ∏ п = 1 ∞ [ ( 1 + z п ) − 1 е z / п ] < Displaystyle Gamma (z) = < frac > > prod _ ^ < infty>left [ left (1 + < frac > right) ^ <- 1>e ^ right]>

Многие сложные функции определяются бесконечная серия, или непрерывные дроби. Фундаментальным соображением при анализе этих бесконечно длинных выражений является определение части комплексной плоскости, в которой они сходятся к конечному значению. Как показывают следующие примеры, разрез в плоскости может облегчить этот процесс.

Рассмотрим функцию, определяемую бесконечным рядом

С z 2 = (−z) 2 для каждого комплексного числа z, ясно что ж(z) является даже функция из z, поэтому анализ можно ограничить половиной комплексной плоскости. А поскольку серия не определена, когда

имеет смысл разрезать плоскость по всей мнимой оси и установить сходимость этого ряда там, где действительная часть z не равняется нулю, прежде чем приступить к более трудной задаче исследования ж(z) когда z это чисто мнимое число. [примечание 7]

Это можно показать который ж(z) сходится к конечному значению тогда и только тогда, когда z не является отрицательным действительным числом такое, что z [8]

Склеивание отрезанной плоскости обратно вместе

У нас есть уже видел как отношения

ш = ж ( z ) = ± z = z 1 / 2 < displaystyle w = f (z) = pm < sqrt > = z ^ <1>>

можно преобразовать в однозначную функцию, разделив область определения ж на два несвязанных листа. Также можно «склеить» эти два листа вместе, чтобы сформировать единый Риманова поверхность на котором ж(z) = z 1/2 можно определить как голоморфную функцию, образ которой есть весь ш-плоскость (кроме точки ш = 0 ). Вот как это работает.

Формальная дифференциация показывает, что

откуда можно заключить, что производная от ж существует и конечна всюду на римановой поверхности, кроме тех случаев, когда z = 0 (то есть, ж голоморфно, кроме случаев, когда z = 0 ).

Каким образом риманова поверхность функции

Использование комплексной плоскости в теории управления

Еще одно связанное использование комплексной плоскости с Критерий устойчивости Найквиста. Это геометрический принцип, который позволяет определить стабильность замкнутой системы обратной связи путем проверки Сюжет Найквиста амплитуды разомкнутого контура и фазовой характеристики как функции частоты (или контура функция передачи) в комплексной плоскости.

Квадратичные пространства

Другие значения слова «комплексная плоскость»

В предыдущих разделах этой статьи комплексная плоскость рассматривается с точки зрения геометрического представления комплексных чисел.Хотя такое использование термина «комплексная плоскость» имеет долгую и богатую математически историю, это ни в коем случае не единственное математическое понятие, которое можно охарактеризовать как «комплексная плоскость». Есть как минимум три дополнительных возможности.

Терминология

Хотя терминология «сложная плоскость» является исторически принятой, объект можно было бы более уместно назвать «сложная линия», поскольку он является одномерным. комплексное векторное пространство.

Источник

Комплексная плоскость

Содержание

Условные обозначения [ править ]

z = x + i y = | z | ( cos ⁡ θ + i sin ⁡ θ ) = | z | e i θ <\displaystyle z=x+iy=|z|\left(\cos \theta +i\sin \theta \right)=|z|e^>

Диаграмма Аргана [ править ]

Диаграмма Аргана относится к геометрическому графику комплексных чисел в виде точек z = x + iy с использованием оси x в качестве действительной оси и оси Y в качестве мнимой оси. [3] Такие участки названы в честь Жана-Робера Аргана (1768–1822), хотя впервые они были описаны норвежско-датским землеустроителем и математиком Каспаром Весселем (1745–1818). [примечание 4] Диаграммы Аргана часто используются для построения положений нулей и полюсов функции на комплексной плоскости.

Стереографические проекции [ править ]

Может быть полезно думать о комплексной плоскости, как если бы она занимала поверхность сферы. Для сферы единичного радиуса поместите ее центр в начало комплексной плоскости, сориентировав ее так, чтобы экватор на сфере совпадал с единичным кругом на плоскости, а северный полюс находился «над» плоскостью.

Это не единственная возможная, но правдоподобная стереографическая ситуация проекции сферы на плоскость, состоящую из двух или более значений. Например, северный полюс сферы может быть помещен поверх начала координат z = −1 в плоскости, касательной к окружности. Детали особого значения не имеют. Любая стереографическая проекция сферы на плоскость создаст одну «точку в бесконечности», и она отобразит линии широты и долготы на сфере в круги и прямые линии, соответственно, на плоскости.

Разрезание самолета [ править ]

При обсуждении функций комплексной переменной часто бывает удобно думать о разрезе в комплексной плоскости. Эта идея естественно возникает в нескольких различных контекстах.

Многозначные отношения и точки ветвления [ править ]

Рассмотрим простое двузначное отношение

y = g ( x ) = x = x 1 / 2 <\displaystyle y=g(x)=<\sqrt >\ =x^<1>>

Очевидно, что когда z движется полностью по кругу, w очерчивает только половину круга. Таким образом, одно непрерывное движение в комплексной плоскости преобразовало положительный квадратный корень e 0 = 1 в отрицательный квадратный корень e iπ = −1.

Отрезок ветви в этом примере не обязательно должен лежать вдоль действительной оси. Это даже не обязательно должна быть прямая линия. Подойдет любая непрерывная кривая, соединяющая начало координат z = 0 с бесконечно удаленной точкой. В некоторых случаях отрезок ветви даже не должен проходить через бесконечно удаленную точку. Например, рассмотрим отношения

Ограничение области мероморфных функций [ править ]

Γ ( z ) = e − γ z z ∏ n = 1 ∞ [ ( 1 + z n ) − 1 e z / n ] <\displaystyle \Gamma (z)=<\frac >>\prod _^<\infty >\left[\left(1+<\frac >\right)^<-1>e^\right]>

Рассмотрим функцию, определяемую бесконечным рядом

Склеивание отрезанных плоскостей обратно вместе [ править ]

w = f ( z ) = ± z = z 1 / 2 <\displaystyle w=f(z)=\pm <\sqrt >=z^<1>>

может быть преобразована в однозначную функцию, разделив область определения f на два несвязанных листа. Также возможно «склеить» эти два листа вместе, чтобы сформировать единую риманову поверхность, на которой f ( z ) = z 1/2 может быть определена как голоморфная функция, образ которой представляет собой всю w- плоскость (за исключением точки w = 0 ). Вот как это работает.

Формальная дифференциация показывает, что

f ( z ) = z 1 / 2 ⇒ f ′ ( z ) = 1 2 z − 1 / 2 <\displaystyle f(z)=z^<1>\quad \Rightarrow \quad f^<\prime >(z)=<\textstyle <\frac <1><2>>>z^<-1/2>>

из чего мы можем заключить, что производная f существует и конечна всюду на римановой поверхности, за исключением случая, когда z = 0 (то есть f голоморфна, кроме случая z = 0 ).

Каким образом риманова поверхность функции

Использование комплексной плоскости в теории управления [ править ]

Квадратичные пространства [ править ]

Другие значения «комплексной плоскости» [ править ]

В предыдущих разделах этой статьи комплексная плоскость рассматривается с точки зрения геометрического представления комплексных чисел. Хотя такое использование термина «комплексная плоскость» имеет долгую и богатую математически историю, это ни в коем случае не единственное математическое понятие, которое можно охарактеризовать как «комплексная плоскость». Есть как минимум три дополнительных возможности.

Терминология [ править ]

Источник

Комплексные числа

Алгебраическая форма записи комплексных чисел

Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме

Комплексно сопряженные числа

Модуль комплексного числа

Деление комплексных чисел, записанных в алгебраической форме

Изображение комплексных чисел радиус-векторами на координатной плоскости

Аргумент комплексного числа

Тригонометрическая форма записи комплексного числа

Формула Эйлера. Экспоненциальная форма записи комплексного числа

Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме

Извлечение корня натуральной степени из комплексного числа

Алгебраическая форма записи комплексных чисел

Множеством комплексных чисел называют множество всевозможных пар (x, y) вещественных чисел, на котором определены операции сложения, вычитания и умножения по правилам, описанным чуть ниже.

Тригонометрическая и экспоненциальная формы записи комплексных чисел будут изложены чуть позже.

Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме

Комплексно сопряженные числа

Модуль комплексного числа

Модулем комплексного числа z = x + i y называют вещественное число, обозначаемое | z | и определенное по формуле

Для произвольного комплексного числа z справедливо равенство:

а для произвольных комплексных чисел z₁ и z₂ справедливы неравенства:

Деление комплексных чисел, записанных в алгебраической форме

Деление комплексного числа z₁ = x₁ + i y₁ на отличное от нуля комплексное число z₂ = x₂ + i y₂ осуществляется по формуле

Используя обозначения модуля комплексного числа и комплексного сопряжения, частное от деления комплексных чисел можно представить в следующем виде:

Деление на нуль запрещено.

Изображение комплексных чисел радиус-векторами координатной плоскости

Рассмотрим плоскость с заданной на ней прямоугольной декартовой системой координат Oxy и напомним, что радиус-вектором на плоскости называют вектор, начало которого совпадает с началом системы координат.

При таком представлении комплексных чисел сумме комплексных чисел соответствует сумма радиус-векторов, а произведению комплексного числа на вещественное число соответствует произведение радиус–вектора на это число.

Аргумент комплексного числа

Считается, что комплексное число нуль аргумента не имеет.

Тогда оказывается справедливым равенство:

(3)

(4)

а аргумент определяется в соответствии со следующей Таблицей 1.

Для того, чтобы не загромождать запись, условимся, не оговаривая этого особо, символом k обозначать в Таблице 1 произвольное целое число.

Таблица 1. – Формулы для определения аргумента числа z = x + i y

y z

Расположение числа z	Знаки x и y	Главное значение аргумента	Аргумент	Примеры
Положительная вещественная полуось
Положительная мнимая полуось
Второй квадрант
Отрицательная вещественная полуось	Положительная вещественная полуось
Знаки x и y
Главное значение аргумента	0
Аргумент	φ = 2kπ
Примеры

Главное
значение
аргументаАргументПримерыГлавное
значение
аргументаАргументПримерыГлавное
значение
аргументаАргументПримеры

x zТретий
квадрантЗнаки x и y

x zОтрицательная
мнимая
полуосьЗнаки x и y

y zЧетвёртый
квадрантЗнаки x и y

Положительная вещественная полуось

Главное значение аргумента:

Расположение числа z :

Главное значение аргумента:

Расположение числа z :

Положительная мнимая полуось

Главное значение аргумента:

Расположение числа z :

Главное значение аргумента:

Расположение числа z :

Отрицательная вещественная полуось

Отрицательная мнимая полуось

x z = x + i y может быть записано в виде

Формула Эйлера. Экспоненциальная форма записи комплексного числа

В курсе «Теория функций комплексного переменного», который студенты изучают в высших учебных заведениях, доказывается важная формула, называемая формулой Эйлера :

Из формулы Эйлера (6) и тригонометрической формы записи комплексного числа (5) вытекает, что любое отличное от нуля комплексное число z = x + i y может быть записано в виде

Из формулы (7) вытекают, в частности, следующие равенства:

а из формул (4) и (6) следует, что модуль комплексного числа

Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме

Экспоненциальная запись комплексного числа очень удобна для выполнения операций умножения, деления и возведения в натуральную степень комплексных чисел.

Действительно, умножение и деление двух произвольных комплексных чисел и записанных в экспоненциальной форме, осуществляется по формулам

Таким образом, при перемножении комплексных чисел их модули перемножаются, а аргументы складываются.

При делении двух комплексных чисел модуль их частного равен частному их модулей, а аргумент частного равен разности аргументов делимого и делителя.

Возведение комплексного числа z = r e iφ в натуральную степень осуществляется по формуле

Другими словами, при возведении комплексного числа в степень, являющуюся натуральным числом, модуль числа возводится в эту степень, а аргумент умножается на показатель степени.

Извлечение корня натуральной степени из комплексного числа

Пусть — произвольное комплексное число, отличное от нуля.

Для того, чтобы решить уравнение (8), перепишем его в виде

следствием которых являются равенства

(9)

Из формул (9) вытекает, что уравнение (8) имеет n различных корней

(10)

то по формуле (10) получаем:

Источник