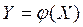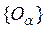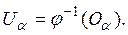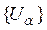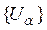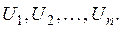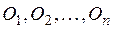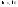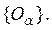что такое компакт матанализ

Научный форум dxdy

Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки

Правила форума

В этом разделе нельзя создавать новые темы.

Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».

Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.

Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.

Компакт в матанализе

Объясните плз что такое компакт? (можно на пальцах)

В Кудрявцеве (учебник матана, 2-й том) дано такое определение:

Ничего не пойму: на уровне выражений и логических связок вроде бы все прозрачно ясно, но все вместе.

Заслуженный участник

Заслуженный участник

Заслуженный участник

Понятие компактности важно для доказательства теорем существования в случае, когда не гарантирована единственность. При доказательстве обычно строится некоторая последовательность, которая, как можно надеяться, даст в пределе то, что нужно. Если она сходится. Но обычно если можно доказать сходимость, то удаётся аналогичными средствами доказать и единственность решения. А если единственности заведомо нет? Тогда и пригождаются соображения компактности: выделяем из построенной последовательности хоть что-то сходящееся, а там авось и что-то получится.

Заслуженный участник

Заслуженный участник

Заслуженный участник

1. Какая, нафиг, предкомпактность: ТС, наверняка, интересуется конечно-мерным случаем, в котором понятие предкомпактности малосодержательно.

2. Не понимаю, почему никто до сих пор не дал стандартного определения компактности: множество компактно, если из любого открытого покрытия можно выделить конечное подпокрытие.

Именно это и работает, когда хотят перейти от локальных к глобальным свойствам, например, от непрерывности в точке к равномерной непрерывности.

Именно так и определяю, надеюсь тут ни с кем разногласий не возникнет.
Только беда в том, что для конечномерного евклидова пространства предкомпактность множества эквивалентна его ограниченности:)

И что вам было интересно?

Заслуженный участник

Именно так и определяю, надеюсь тут ни с кем разногласий не возникнет.

Мне было интересно, как вы так лихо, хотя ещё не понятно как определили, предкомпактное пространство, свои соображения по поводу предкомпактного множества я высказал и они подкреплены определениями почти в любом учебнике по топологии, но насчёт пространства впервые слышу.

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей

Источник

(5)Компакт.Критерии компакта.

Множество E называется компактом, если из любой последовательности точек этого множества можно выделить подпоследовательность, сходящуюся в точке из этого же множества

Теорема (критерий компактов):

Для того чтобы множество E было компактом необходимо и достаточно чтобы оно было замкнутым и ограниченным.

Пусть Е – неограниченно сверху, тогда , значит из нее нельзя выделить подпоследовательность сходящуюся в точке из Е, отсюда следует что Е – не компакт, получим противоречие, значит Е – ограниченно

т.к. Е – не компакт, то можно выделить из последовательности подпоследовательность, которая будет сходится в какой нибудь точке из множества Е,с другой стороныт.к.— предел всей последовательности, получается взяв любую предельную точку для Е, получается что Е – замкнутое

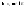
Е – замкнуто и ограниченно , т.к. Е ограниченноограниченнопо лемме Б.Б. из нее можно выделить сходящуюся подпоследовательность, но учитывая, что Е – замкнутое по критерию замкнутости

(6)Теоремы Вейерштрасса о непрерывных функциях.

1) Теоремы Вейерштрасса о непрерывных функциях

Если непрерывна на компакте Е, то— тоже компакт

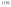
Рассмотрим и, для каждого изизможно выделить сходящуюся подпоследовательность, а т.к. функция непрерывна на У, тоПолучаемт.е. множество— компакт

Если G – компакт, то — ограниченно,, возьмем последовательность чиселпо критериюsup, , ноG – замкнуто по критерию замкнутости

Первая, вторая теоремы Вейерштрасса:

Всякая непрерывная на компакте функция: 1) неограниченна на нем

2) достигает на нем свои набольшее и наименьшее значения

1) Т.к. Е – компакт, то по лемме 1 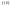тоже компакт, т.е. ограниченна

2) По лемме 2 , т.е. есть точка являющаясяsup и есть точка inf

(7)Равномерная непрерывность ф ункции. Теорема Кантора о равномерной непрерывности

Рассмотрим непрерывную на Е, т.е.

Ясно, что для различных точек — различно, если можно подобратьподходящее сразу для всех точек, то функция называется равномерной, непрерывной.

Функция называется равномерной, непрерывной на Е, если для любого,

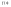
Ясно, что для любая равномерная непрерывная функция будет и просто непрерывной, такое что 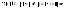,обратное – не верно.

Есть частный случай, когда из непрерывности следует равномерная непрерывность.

Теорема (Кантора о равномерной непрерывности):

Всякая непрерывная на компакте функция равномерно непрерывна на нем.

Фиксируем Пусть не существуетдля которого бы выполнялись условия равномерной непрерывности

Возьмем последовательность не отрицательных чисел По предположению (1)По лемме Б. Б. из ограниченной последовательностиможно выделить подпоследовательность сходящуюся в некоторой точкеБудем считать что уже сама последовательностьсходится кТ.к., тоВ виду того, что— непрерывнаа это противоречит тому, чтонепрерывная на компакте функция равномерно непрерывна

Источник

Расширенная комплексная плоскость, как и замкнутая числовая сфера, являются компактами.

задан 28 Фев ’17 2:06

Романенко
183 ● 1 ● 2 ● 11
60&#037 принятых

@Романенко: я бы в первую очередь обратил внимание на неэффективность такого способа изучения математики. Берутся какие-то фразы из источников типа Википедии, потом они как-то трактуются.

Прежде всего, тут смешаны как важные понятия (компактность), так и совершенно «левые», порождающие лишние вопросы. О том, что такое компактное топологическое пространство, лучше прочитать в учебниках. Включая примеры и свойства. Что касается двумерной сферы, то это обычное школьное геометрическое понятие. Конечно, она замкнута в топологическом смысле слова (определение также лучше прочитать в книге).

@Романенко: в учебниках часто могут быть использованы ссылки на факты, считающиеся известными. Иногда могут использоваться иллюстрации, и там язык может быть менее строгим. Но у этих вещей разное назначение, и смешивать одно с другим не следует.

Для понимания этих вещей нужно хорошо понимать, что такое стереографическая проекция. Но это стандартная вещь, она много где изложена. Топологические понятия типа открытого, замкнутого, компактного множества надо знать хотя бы для частного случая, то есть для R^n. Но вообще-то, более сложные вещи лучше изучать после элементарных.

@falcao,простите, но еще хотел бы попросить: скиньте пожалуйста ссылку, где рассказывается про вот эти компакты, если такие знаете(просто предыдущие ссылки очень мне понравились(более менее понятны и просты в моем понимании))

@falcao, А вы можете посоветовать, какие-ниб вот эти элементарные вещи, которые стоит сначала изучить,т.к. очень нужно хорошо понять материал!

@Романенко: годится любой учебник, где говорится об основах общей топологии. Всё это есть даже в учебниках обычного матанализа, написанных на современной основе. Вот почти первая попавшаяся ссылка. Но надо иметь в виду, что нужную для Вас информацию придётся самостоятельно вычленять. Там есть много посторонних сведений, а я говорю о самых основных.

@falcao, о компактности говорится только в последнем параграфе, т.е. здесь все так и надо все понять до этого параграфа и получается начать с метрического пространства? если да,то первый здесь вопрос: как это ( http://prnt.sc/ee7bmt ) понять?

@falcao,абстрактным, т.е. не обязательно расстояние именно м/д точками: могут быть предметы и т.д. или Вы другое имели ввиду?

@falcao, почему одинакового объема?это как однородные величины(пример: целые числа)?

@falcao, вот эти три свойства? если да, то почему именно они важны:это же какие то очевидные свойства!

@Романенко: пример с пластилиновыми фигурками дополнительно комментировать не буду. Если он сходу не понят, значит, он неудачный. Это тот случай, когда действует принцип: «если надо объяснять, то не надо объяснять» (с)

Три свойства очевидны для обычного расстояния на прямой или плоскости. Но они не обязаны выполняться в общем случае, для произвольного правила. Я уже говорил, что правило задания «расстояния» между точками может быть каким угодно.

Источник

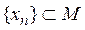
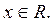
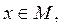
Достаточность. Так как М компактно, то из всякой последовательности можно выбрать подпоследовательность, сходящуюся к некоторому Если М замкнуто, то т. е. М компактно в себе.

Отсюда и из теоремы 1 § 16 вытекает

Следствие. Всякое замкнутое ограниченное подмножество евклидова пространства является компактом.

Теорема 2. Для того чтобы метрическое пространства было компактом, необходимо и достаточно, чтобы оно было: 1) полно, 2) вполне ограничено.

Доказательство этой теоремы представляет собой дословное повторение доказательства теоремы 1 § 16.

Теорема 3. Всякий компакт К содержит конечное или счетное всюду плотное множество.

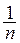
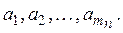
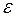
Доказательство. Так как компакт является вполне ограниченным пространством, то для каждого п в К найдется конечная -сеть: Объединение всех этих -сетей представляет собой конечное или счетное множество. Отсюда и из теоремы 4 § 10 вытекает

Следствие. Всякий компакт имеет счетный базис.

Теорема 4. Для того чтобы метрическое пространство R было компактом, необходимо и достаточно каждое из двух условий:

1) Любое открытое покрытие 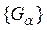пространства R содержит конечное подпокрытие.

2) Любая центрированная[9] система 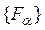замкнутых множеств в R имеет непустое пересечение.

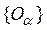
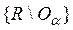
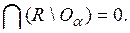
Доказательство. Заметим, прежде всего, что эквивалентность сформулированных двух условий непосредственно вытекает из принципа двойственности (§ 1). Действительно, если — открытое покрытие пространства R, то — система замкнутых множеств, удовлетворяющая условию

(1)

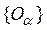
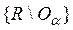
Условие, что из можно выбрать конечное подпокрытие, равносильно тому, что система замкнутых множеств не может быть центрированной, если она имеет пустое пересечение.

Докажем теперь, что условие 1 необходимо и достаточно для того, чтобы R было компактом.

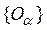
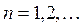
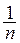
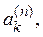
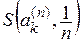
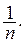
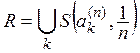
Необходимость. Пусть R — компакт и — его открытое покрытие. Выберем в R для каждого конечную -сеть, состоящую из точек и окружим каждую из этих точек сферой радиуса Ясно, что при любом п

(2)

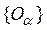
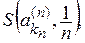
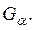
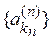
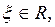
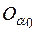
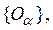
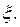
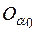
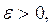
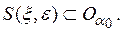
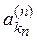
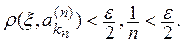
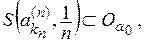
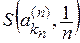
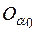
Предположим, что из нельзя выбрать конечной системы множеств, покрывающих R. Тогда при каждом п найдется по крайней мере одна сфера которая не может быть покрыта конечным числом множеств Выберем для каждого п такую сферу и рассмотрим последовательность их центров Так как R — компакт, то существует точка предельная для этой последовательности. Пусть — множество из содержащее Так как открыто, то найдется такое что Выберем теперь номер п и точку так, чтобы Тогда, очевидно, т.е. сфера покрывается даже одним множеством Полученное противоречие доказывает наше утверждение.

Достаточность. Допустим, что пространство R таково, что из всякого его открытого покрытия можно выбрать конечное подпокрытие. Докажем, что R — компакт. Для этого достаточно доказать что R полно и вполне ограничено. Пусть Взяв вокруг каждой точки окрестность получим открытое покрытие R. Выберем из этого покрытия конечное подпокрытие Ясно, что центры этих окрестностей образуют в R конечную -сеть. Так как произвольно, то R вполне ограничено. 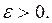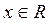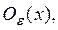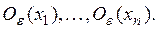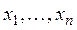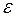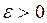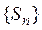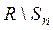Пусть теперь — последовательность вложенных друг в друга замкнутых сфер, радиусы которых стремятся к нулю. Если их пересечение пусто, то множества образуют открытое покрытие R, из которого нельзя выбрать конечного подпокрытия. Таким образом, из условия 1 следует полнота и полная ограниченность, т. е. компактность R.

Теорема 5. Непрерывный образ компакта есть компакт.

Доказательство. Пусть X — компакт и — его непрерывный образ. Пусть, далее, — открытое покрытие пространства Y. Положим Так как при непрерывном отображении прообраз открытого множества открыт, то — открытое покрытие пространства X. Так как X — компакт, то из покрытия можно выбрать конечное подпокрытие Тогда соответствующие множества образуют конечное подпокрытие покрытия

Источник