что такое коэффициент искажения в аксонометрии

Черчение. 10 класс

§ 17. Основные положения аксонометрического проецирования

Основные положения аксонометрического проецирования

Проецирование предмета на плоскости проекций дает нам представление о форме самого предмета только с одной стороны. Чтобы получить представление о форме предмета в целом, нужно проанализировать и сравнить между собой отдельные его проекции. Предмет можно спроецировать на плоскость проекций таким образом, чтобы на созданном изображении было видно сразу несколько его сторон. Полученное таким образом изображение называется наглядным. Его используют для реализации технического замысла автора при выполнении проектирования и конструирования разных объектов (рис. 53).
Для получения наглядного изображения предмета используют аксонометрическую проекцию (рис. 54).

Аксонометрическая проекция — это изображение, полученное при параллельном проецировании предмета вместе с осями прямоугольных координат на произвольную плоскость.

Слово аксонометрия — греческое. В переводе оно означает «измерение по осям» (аксон — ось, метрео — измеряю).

Проецируемый предмет располагают относительно координатных осей х, у, z и вместе с ними проецируют его на произвольную плоскость. Эта плоскость называется плоскостью аксонометрических проекций. Проекции координатных осей называются аксонометрическими осями (см. рис. 54).

Виды аксонометрических проекций.

Аксонометрическое изображение предмета получается прямоугольным (а) и косоугольным (б) проецированием.
Проецирующие лучи в прямоугольной аксонометрической проекции перпендикулярны плоскости проекции. К прямоугольным аксонометрическим проекциям относятся изометрическая и диметрическая проекции.
Проецирующие лучи в косоугольной аксонометрической проекции направлены под углом к плоскости проекций. К косоугольным аксонометрическим проекциям относятся фронтальная изометрическая, горизонтальная изометрическая и фронтальная диметрическая проекции.

Какой вид аксонометрической проекции (прямоугольную или косоугольную) вы будете использовать для наглядного изображения объекта? Свой выбор объясните.

Коэффициент искажения. Все виды аксонометрических проекций характеризуются двумя параметрами: направлением аксонометрических осей и коэффициентами искажения по этим осям.

Коэффициент искажения (k) — отношение аксонометрической единицы измерения к натуральной.

В зависимости от расположения координатных аксонометрических осей относительно аксонометрических проекций получаются различные аксонометрические проекции: прямоугольная изометрическая проекция (сокращенно — изометрия), прямоугольная диметрическая проекция (или диметрия), косоугольные фронтальная и горизонтальная изометрия и фронтальная диметрия.
Например, в прямоугольной изометрической проекции оксонометрические оси располагаются по отношению друг к другу под углом 120°.
Коэффициенты искажения различны в изометрических и диметрических аксонометрических проекциях. В изометрической проекции коэффициент (k) равен единице, т. е. по осям х, y, z выполняют проекцию без искажения. Диметрическая проекция выполняется с коэффициентом искажения (k) по оси y, равным 0,5, а по осям z и х — равным единице.

Объясните, в чем отличие изометрической проекции от диметрической.

Наиболее распространенными являются прямоугольная изометрическая (прямоугольная изометрия) и косоугольная фронтальная диметрическая (фронтальная диметрия) проекции, в которых объект изображается в трех проекциях так, чтобы можно было хорошо увидеть его форму с трех сторон.
Способы построения аксонометрических осей. При построении аксонометрических осей прямоугольной изометрии используют один из трех способов.

Правила построения аксонометрических проекций
1. Длина откладывается по оси х, высота — по оси z, ширина — по оси у.
2. Все измерения выполняются только по аксонометрическим осям или прямым, параллельным им.
3. Все прямые линии, параллельные друг другу или осям x, y, z, на комплексном чертеже в аксонометрических проекциях остаются параллельными между собой и соответствующим аксонометрическим осям

В начале 80-х гг. XX в. в компьютерных играх стала активно применяться изометрическая проекция. Это быстрая и эффективная симуляция трехмерного пространства, которая дает иллюзию глубины без большого количества дорогостоящих вычислений. Раньше большинство игр имели вид сверху или вид сбоку. Первыми играми, которые использовали изометрию, были Zaxxon и Qbert. Сейчас, несмотря на развитие 3D-технологий, игры с изометрическим видом все еще очень популярны, особенно ролевые и стратегии.

Источник

Аксонометрия

Сообщение об ошибке

СОДЕРЖАНИЕ

Аксонометрия

Аксонометрия (от греч. axcon – ось и metreo – измеряю) дает наглядное изображение предмета на одной плоскости.

Изображение предмета в аксонометрии получается путем параллельного проецирования его на одну плоскость проекций вместе с осями прямоугольных координат, к которым этот предмет отнесен.

Коэффициенты искажения по осям в аксонометрии определяют отношением аксонометрических координатных отрезков к их натуральной величине при одинаковых единицах измерения.

Натуральные коэффициенты искажения обозначают:

В зависимости от сравнительной величины коэффициентов искажения по осям различают три вида аксонометрии:

Изометрия – все три коэффициента искажения равны между собой: u=v=w.

Диметрия – два коэффициента искажения равны между собой и отличаются от третьего u=v≠w; v=w≠u; u=w≠v.

Триметрия – все три коэффициента искажения не равны между собой: u≠v≠w.

В зависимости от направления проецирования аксонометрические проекции разделяют на прямоугольные (направление проецирования перпендикулярно плоскости аксонометрических проекций) и косоугольные (направление проецирования не перпендикулярно плоскости аксонометрических проекций).

Прямоугольные проекции

Изометрия

Положение аксонометрических осей приведено на рис.1.

Рис.1. Оси изометрии

Коэффициент искажения по осям x, y, z равен 0,82.

Изометрию для упрощения, как правило, выполняют без искажения по осям x, y, z, т. е. приняв коэффициент искажения равным 1.

Построенное таким образом изображение будет больше самого предмета в 1,22 раза, т.е. масштаб изображения будет М 1,22:1.

Окружности, лежащие в плоскостях, параллельных плоскостям проекций проецируются на аксонометрическую плоскость проекций в эллипсы (рис.2). Если изометрическую проекцию выполняют без искажения по осям x, y, z, то большая ось эллипсов 1, 2, 3 равна 1,22, а малая ось – 0,71 диаметра окружности. Если изометрическую проекцию выполняют с искажением по осям x, y, z, то большая ось эллипсов 1, 2, 3 равна диаметру окружности, а малая ось – 0,58 диаметра окружности.

Пример изометрической проекции детали приведен на рис.3.

Рис.3. Деталь в изометрии

Диметрия

Положение аксонометрических осей приведено на рис.4.

Рис.4. Оси диметрии

Коэффициент искажения по оси y равен 0,47, а по осям x и z – 0,94.

Диметрическую проекцию, как правило, выполняют без искажения по осям x и z и с коэффициентом искажения 0,5 по оси y.

Аксонометрический масштаб будет М 1,06:1.

Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются на аксонометрическую плоскость проекций в эллипсы (рис.5). Если диметрическую проекцию выполняют без искажения по осям x и z, то большая ось эллипсов 1, 2, 3 равна 1,06 диаметра окружности, а малая ось эллипса 1 – 0,95, эллипсов 2 и 3 – 0,35 диаметра окружности. Если диметрическую проекцию выполняют с искажением по осям x и z, то большая ось эллипсов 1, 2, 3 равна диаметру окружности, а малая ось эллипса 1 – 0,9, эллипсов 2 и 3 – 0,33 диаметра окружности.

Пример диметрической проекции детали приведен на рис.6.

Рис.6. Деталь в диметрии

Косоугольные проекции

Изометрия фронтальная

Положение аксонометрических осей приведено на рис.7.

Рис.7. Оси фронтальной изометрии

Допускается применять фронтальные изометрические проекции с углом наклона оси у 30 и 60°.

Фронтальную изометрическую проекцию выполняют без искажения по осям x, y, z.

Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на аксонометрическую плоскость в окружности, а окружности, лежащие в плоскостях, параллельных горизонтальной и профильной плоскостям проекций, – в эллипсы (рис.8). Большая ось эллипсов 2 и 3 равна 1,3, а малая ось – 0,54 диаметра окружности.

Пример фронтальной изометрической проекции детали приведен на рис.9.

Рис.9. Деталь в фронтальной изометрии

Изометрия горизонтальная

Положение аксонометрических осей приведено на рис.10.

Рис.10. Оси горизонтальной изометрии

Допускается применять горизонтальные изометрические проекции с углом наклона оси y 45 и 60°, сохраняя угол между осями x и y 90°.

Горизонтальную изометрическую проекцию выполняют без искажения по осям x, y и z.

Окружности, лежащие в плоскостях, параллельных горизонтальной плоскости проекций, проецируются на аксонометрическую плоскость проекций в окружности, а окружности, лежащие в плоскостях, параллельных фронтальной и профильной плоскостям проекций – в эллипсы (рис.11). Большая ось эллипса 1 равна 1,37, а малая ось – 0,37 диаметра окружности. Большая ось эллипса 3 равна 1,22, а малая ось – 0,71 диаметра окружности.

Пример горизонтальной изометрической проекции приведен на рис.12.

Рис.12. Деталь в горизонтальной изометрии

Диметрия фронтальная

Положение аксонометрических осей приведено на рис.13.

Рис.13. Оси фронтальной диметрии

Допускается применять фронтальные диметрические проекции с углом наклона оси у 30 и 60°.

Коэффициент искажения по оси y равен 0,5, а по осям x и z – 1.

Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на аксонометрическую плоскость проекций в окружности, а окружности, лежащие в плоскостях, параллельных горизонтальной и профильной плоскостям проекций, – в эллипсы (рис.14). Большая ось эллипсов 2 и 3 равна 1,07, а малая ось – 0,33 диаметра окружности.

Пример фронтальной диметрической проекции детали приведен на рис.15.

Источник

Что такое коэффициент искажения в аксонометрии

Контрольные задания по теме: эпюр № 6

Для наглядного изображения предметов (изделий или их составных частей) рекомендуется применять аксонометрические проекции, выбирая в каждом отдельном случае наиболее подходящую из них.

Сущность метода аксонометрического проецирования заключается в том, что заданный предмет вместе с координатной системой, к которой он отнесен в пространстве, параллельным пучком лучей проецируется на некоторую плоскость. Направление проецирования на аксонометрическую плоскость не совпадает ни с одной из координатных осей и не параллельно ни одной из координатных плоскостей.

Все виды аксонометрических проекций характеризуются двумя параметрами: направлением аксонометрических осей и коэффициентами искажения по этим осям. Под коэффициентом искажения понимается отношение величины изображения в аксонометрической проекции к величине изображения в ортогональной проекции.

В зависимости от соотношения коэффициентов искажения аксонометрические проекции подразделяются на:

— изометрические, когда все три коэффициента искажения одинаковы (k_x=k_y=k_z);

— диметрические, когда коэффициенты искажения одинаковы по двум осям, а третий не равен им (k_x= k_z ≠k_y);

— триметрические, когда все три коэффициенты искажения не равны между собой (k_x≠k_y≠k_z).

В зависимости от направления проецирующих лучей аксонометрические проекции подразделяются на прямоугольные и косоугольные. Если проецирующие лучи перпендикулярны аксонометрической плоскости проекций, то такая проекция называется прямоугольной. К прямоугольным аксонометрическим проекциям относятся изометрическая и диметрическая. Если проецирующие лучи направлены под углом к аксонометрической плоскости проекций, то такая проекция называется косоугольной. К косоугольным аксонометрическим проекциям относятся фронтальная изометрическая, горизонтальная изометрическая и фронтальная диметрическая проекции.

В прямоугольной изометрии углы между осями равны 120°. Действительный коэффициент искажения по аксонометрическим осям равен 0,82, но на практике для удобства построения показатель принимают равным 1. Вследствие этого аксонометрическое изображение получается увеличенным в 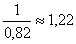раза.

Изометрические оси изображены на рисунке 57.

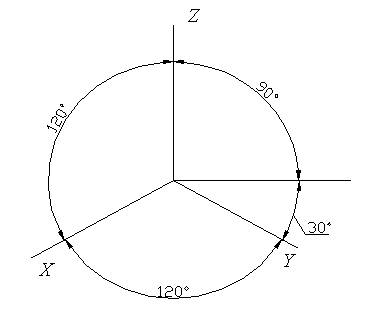
Рисунок 57

Рисунок 58

Построение изометрической проекции шестиугольника представлено на рисунке 59. Для этого необходимо отложить по оси X радиус описанной окружности шестиугольника в обе стороны относительно начала координат. Затем, по оси Y отложить величину размера под ключ, из полученных точек провести линии параллельно оси X и отложить по ним величину стороны шестиугольника.

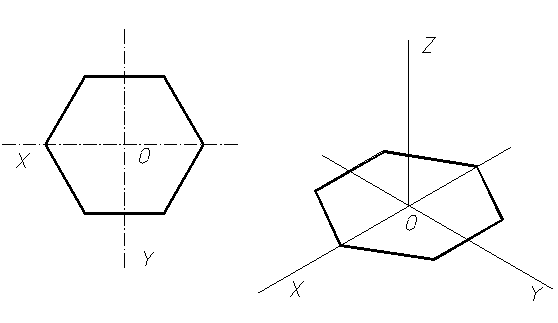
Рисунок 59

Построение окружности в прямоугольной изометрической проекции

Наиболее сложной плоской фигурой для вычерчивания в аксонометрии является окружность. Как известно, окружность в изометрии проецируется в эллипс, но построение эллипса довольно сложно, поэтому ГОСТ 2.317-69 рекомендует вместо эллипсов применять овалы. Существует несколько способов построения изометрических овалов. Рассмотрим один из наиболее распространенных.

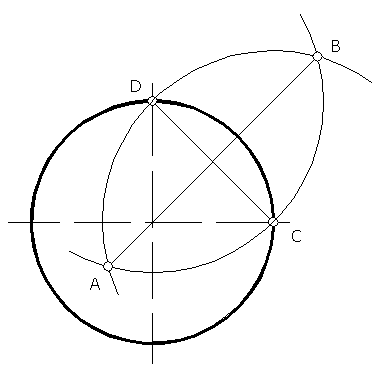
Рисунок 60

Установив направление большой и малой осей овала в зависимости от того, какой координатной плоскости принадлежит окружность, по размерам большой и малой оси проводят две концентрические окружности, в пересечении которых с осями намечают точки О₁, О₂, О₃, О₄, являющиеся центрами дуг овала (рисунок 61).

Для определения точек сопряжения проводят линии центров, соединяя О₁, О₂, О₃, О₄. из полученных центров О₁, О₂, О₃, О₄ проводят дуги радиусами R и R₁. размеры радиусов видны на чертеже.

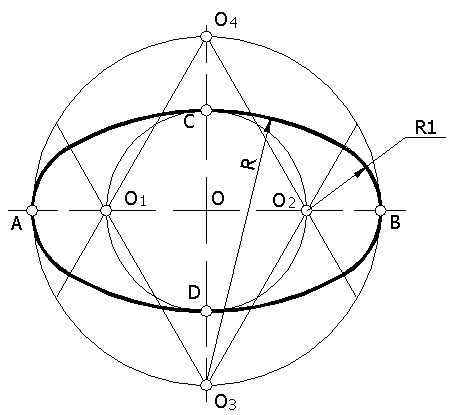
Рисунок 61

Направление осей эллипса или овала зависит от положения проецируемой окружности. Существует следующее правило: большая ось эллипса всегда перпендикулярна к той аксонометрической оси, которая на данную плоскость проецируется в точку, а малая ось совпадает с направлением этой оси (рисунок 62).

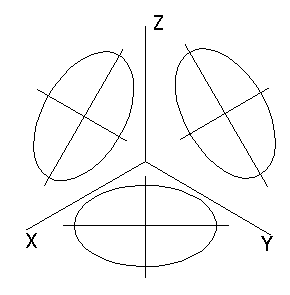
Рисунок 62

Штриховка и изометрической проекции

Линии штриховки сечений в изометрической проекции, согласно ГОСТ 2.317-69, должны иметь направление, параллельное или только большим диагоналям квадрата, или только малым.

Прямоугольной диметрией называется аксонометрическая проекция с равными показателями искажения по двум осям X и Z, а по оси Y показатель искажения в два раза меньше.

По ГОСТ 2.317-69 применяют в прямоугольной диметрии ось Z, расположенную вертикально, ось Х наклонную под углом 7°, а ось Y-под углом 41° к линии горизонта. Показатели искажения по осям X и Z равны 0,94, а по оси Y-0,47. Обычно применяют приведенные коэффициенты k_x=k_z=1, k_y=0,5, т.е. по осям X и Z или по направлениям им параллельным, откладывают действительные размеры, а по оси Y размеры уменьшают в два раза.

Для построения осей диметрии пользуются способом, указанным на рисунке 63, который заключается в следующем:

На горизонтальной прямой, проходящей через точку О, откладывают в обе стороны восемь равных произвольных отрезков. Из конечных точек этих отрезков вниз по вертикали откладывают слева один такой же отрезок, а справа – семь. Полученные точки соединяют с точкой О и получают направление аксонометрических осей X и Y в прямоугольной диметрии.

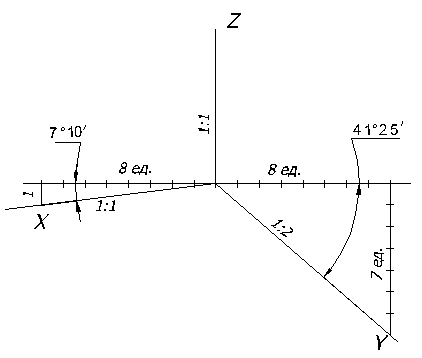
Рисунок 63

Построение диметрической проекции шестиугольника

Рассмотрим построение в диметрии правильного шестиугольника, расположенного в плоскости П₁ (рисунок 64).

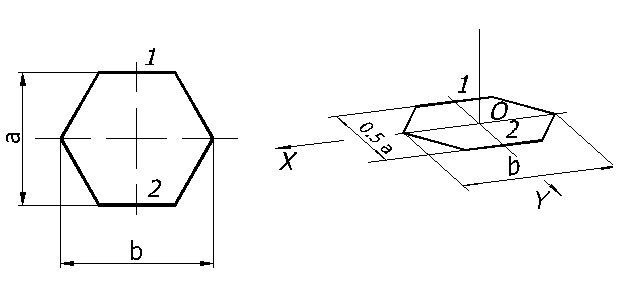
Рисунок 64

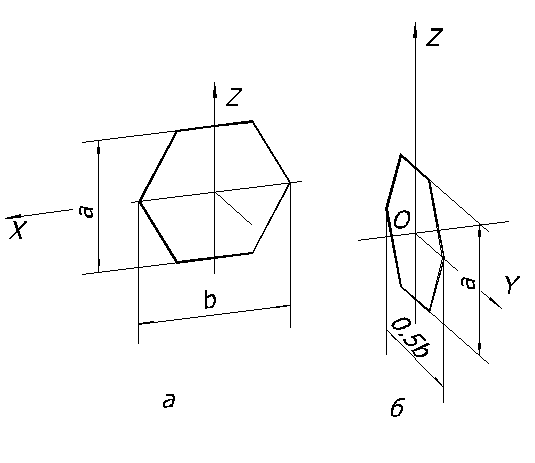
Рисунок 65

Построение окружности в диметрии

В прямоугольной диметрии все окружности изображаются эллипсами,

На практике эллипс заменяется четырехцентровым овалом. Рассмотрим построение овала, заменяющего проекцию окружности, лежащей в горизонтальной и профильной плоскостях (рисунок 66).

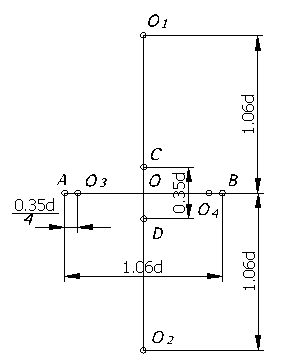
Рисунок 66

Затем, из точек О1 и О2 проводим дуги, радиус которых равен расстоянию до точек С и D, а из точек О3 и О4 – радиусом до точек А и В (рисунок 67).

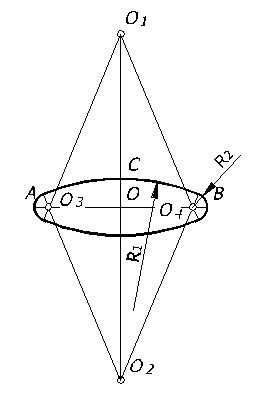
Рисунок 67

Построение овала, заменяющего эллипс, от окружности, расположенной в плоскости П₂, рассмотрим на рисунке 68. Проводим оси диметрии: Х, Y, Z. Малая ось эллипса совпадает с направлением оси Y, а большая перпендикулярна к ней. На осях Х и Z от начала откладываем величину радиуса окружности и получаем точки M, N, K, L, являющиеся точками сопряжения дуг овала. Из точек M и N проводим горизонтальные прямые, которые в пересечении с осью Y и перпендикуляром к ней дают точки О₁, О_2, О_3, О₄ – центры дуг овала (рисунок 68).

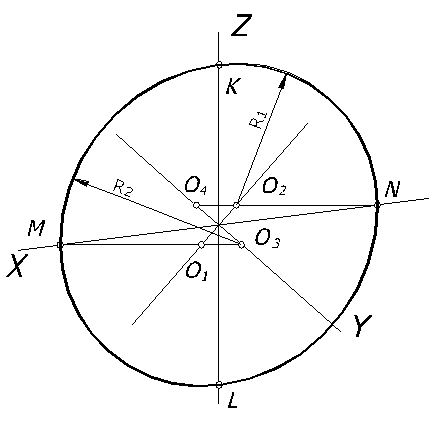
Рисунок 68

Штриховка а прямоугольной диметрии

Линии штриховки разрезов и сечений в аксонометрических проекциях выполняются параллельно одной из диагоналей квадрата, стороны которого расположены в соответствующих плоскостях параллельно аксонометрическим осям (рисунок 69).

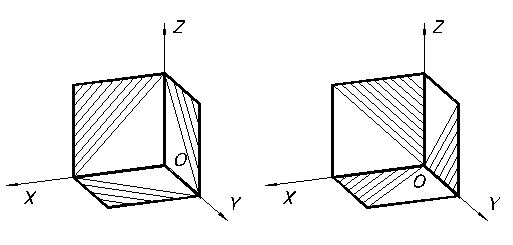
Рисунок 69

© ФГБОУ ВПО Красноярский государственный аграрный университет

Источник

Понятие об аксонометрических проекциях

Наглядные изображения применяют для пояснения чертежей деталей и машин. По ним легче представить форму предмета, чем по чертежу в трёх видах.

Одним из видов наглядных изображений являются аксонометрические изображения.

Аксонометрия в переводе с греческого означает «измерение по осям».

Аксонометрические проекции получают путём проецирования параллельными лучами

предмета, который связан с осями прямоугольных координат, на некоторую плоскость Р (рис. 103).

Таким образом, аксонометрическая проекция – это проекция только на одну плоскость.

Чтобы изображение получилось наглядным, проецирующие лучи не должны быть параллельны ни одной оси координат. Тогда на плоскости Р будут, хоть и с искажениями, изображены все три измерения предмета.

Аксонометрические проекции в зависимости от направления проецирования делятся на два вида: прямоугольные, когда направление проецирования перпендикулярно плоскости Р (угол φ=90°), и косоугольные, когда угол φ≠90°.

Если плоскость Р не параллельна ни одной из координатных плоскостей x,y,z, то на аксонометрической проекции у предмета искажаются все три его измерения. Если же плоскость Р параллельна одной или двум осям координат, то у предмета искажаются размеры соответственно по двум его измерениям или по одному.

Величина искажения определяется коэффициентом искажения, который равен отношению длины аксонометрической проекции отрезка, параллельного соответствующей оси координат, к его действительной длине. Любая аксонометрическая проекция имеет три коэффициента искажения по числу осей координат.

В зависимости от того, разные они или одинаковые, аксонометрические проекции делят на изометрические (коэффициенты искажения равны по всем трём осям) и триметрические (коэффициенты искажения по всем осям разные).

Стандартные виды аксонометрии. Изометрия. Диметрия

Наиболее распространёнными видами аксонометрических проекций являются прямоугольная изометрическая проекция (изометрия) и прямоугольная диметрическая проекция (диметрия), основные правила построения которых определены стандартом.

Прямоугольная изометрия представляет собой аксонометрическую проекцию с направлением проецирования, перпендикулярным к плоскости аксонометрических проекций одинаковыми по всем трём осям коэффициентами искажения, равными 0,82.

Оси изометрии (рис. 104а) составляют между собой углы 120°. Ось Z расположена вертикально. Для упрощения построения коэффициент искажения принимают равным 1.

Изображение при этом получается увеличенным, но вид его не меняется, т.к. сохраняется пропорциональность всех его размеров.

На рис. 104б и в приведены два способа построения осей в изометрии.

Прямоугольная диметрия представляет собой аксонометрическую проекцию с направлением проецирования, перпендикулярным аксонометрической плоскости проекций Р и одинаковыми коэффициентами искажения по осям х и z.

Ось х (рис. 105а) составляет с горизонтальной прямой угол 7°10′, а ось у – угол 41°25′.

Ось z занимает вертикальное положение. На рис. 105б показан графический способ построения осей диметрии.

В диметрии коэффициенты искажения по осям х и z равны 0,94, а по оси у – 0,47. При построениях первый коэффициент округляют до 1, а второй – до 0,5. Таким образом, отрезки, параллельные осям координат х и z, откладывают в натуральную величину, а длину отрезков, параллельных оси у, уменьшают в два раза.

Построение окружности в аксонометрии

Изометрия. Изометрические проекции окружностей, расположенных в плоскостях проекций или в плоскостях, им параллельных, есть эллипсы (рис. 106).

Большие оси этих эллипсов равны l,22Dокр, а малые 0,71Dокр, где Dокр – диаметр изображаемой окружности. Большая ось эллипсов всегда перпендикулярна к той аксонометрической оси, которая отсутствует в плоскости окружности, а малая совпадает с этой осью или параллельна ей.

Практически при построении изометрии окружности эллипс обычно заменяют близким к нему по форме овалом, т.к. построение овала значительно проще.

Наиболее простой способ построения овала показан на рис. 107.

На рис. 108а,б построены изометрии окружностей, расположенных во фронтальной и профильной плоскостях.

Окружности, расположенные во фронтальной плоскости, проецируются в виде эллипсов с большой осью, равной 1,06Dокр, а малой – 0,94Dокр. Большие оси эллипсов, как и в изометрии, перпендикулярны к той аксонометрической оси, которая отсутствует в данной плоскости, а малые оси совпадают с направлением этой оси.

Диметрии окружностей (эллипсы) обычно заменяют овалами, размеры осей которых равны размерам соответствующих осей эллипсов. Построение этих овалов показано на рис. 110. На рис. 110а построения понятны по чертежу.

На рис. 110б строим оси диметрии х_р, у_р, z_р. Затем строим прямую, перпендикулярную оси у_р. Отложив на осях х_р и z_р радиус заданной окружности, получим точки М, К, N, L, которые являются точками сопряжения дуг овала. Через точки М и N проводим горизонтальные прямые. В пересечении этих прямых с осью у_р и перпендикуляром к ней получим точки О₁, О₂, О₃, О₄. Из центров O₁ и О₃ опишем дуги радиусом R₁=О₃ K, а из центров О₂ и О₄ – дуги радиусом R₂=О₂M.

Аксонометрические изображения предметов

Приступая к построению аксонометрической проекции предмета, следует выбрать вид аксонометрии, обеспечивающий наибольшую наглядность изображения. Затем предмет связывают с системой прямоугольных координат, оси которой обычно совмещают с осями симметрии предмета. Только после этого можно приступить к построению аксонометрии.

Построение аксонометрии предмета обычно начинают с построения аксонометрии одной из его проекций (вторичной проекции). Затем полученное изображение дополняют построением третьего измерения всех его точек.

На рис. 111 показан пример построения прямоугольной изометрии предмета через построение его горизонтальной проекции.

На рис. 112 приведен пример построения прямоугольной изометрии детали путём построения её вторичной фронтальной проекции.

Для выявления внутренней формы предмета, изображённого в аксонометрии, в некоторых случаях применяют разрезы, которые условно называют вырезами. При этом используют две секущие плоскости, обычно совпадающие с плоскостями симметрии предмета (рис. 113).

рис. 111 рис. 112 рис. 113

Линии штриховки сечений в аксонометрических проекциях наносят параллельно одной из диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях. Стороны квадратов параллельны аксонометрическим осям (рис. 114).

Источник