что такое коэффициент диффузии
Коэффициент диффузии
Коэффицие́нт диффу́зии — количественная характеристика скорости диффузии, равная количеству вещества (в массовых единицах), проходящего в единицу времени через участок единичной площади (например, 1 м²) при градиенте концентрации, равном единице (соответствующем изменению 1 моль/л → 0 моль/л на единицу длины). Коэффициент диффузии определяется свойствами среды и типом диффундирующих частиц.
Зависимость коэффициента диффузии от температуры в простейшем случае выражается законом Аррениуса:

где 



См. также
Полезное
Смотреть что такое «Коэффициент диффузии» в других словарях:
коэффициент диффузии — носителей заряда; коэффициент диффузии Абсолютная величина отношения плотности потока подвижных носителей заряда одного типа (т. е. электронов проводимости или дырок) к градиенту их концентрации в отсутствие электрического и магнитного полей.… … Политехнический терминологический толковый словарь
коэффициент диффузии — Коэффициент пропорциональности, представляющий количество вещества, диффундирующего сквозь единицу площади при единичном градиенте концентрации за единицу времени. [http://www.manual steel.ru/eng a.html] Тематики металлургия в целом EN diffusion… … Справочник технического переводчика
коэффициент диффузии — [diffusion constant] коэффициент пропорциональности в законах диффузии Фика (D, м2/с). По 1 му закону Фика dm/dс = DS(dC/dX), где m количество диффундируемого вещества, т время, S площадь, С концентрация, X направление диффузноного потока … Энциклопедический словарь по металлургии
коэффициент диффузии — difuzijos koeficientas statusas T sritis fizika atitikmenys: angl. diffusion coefficient; diffusion constant; diffusivity vok. Diffusionskoeffizient, m; Diffusionskonstante, f rus. коэффициент диффузии, m; постоянная диффузии, f pranc.… … Fizikos terminų žodynas
Коэффициент диффузии — Diffusion coefficient Коэффициент диффузии. Коэффициент пропорциональности, представляющий количество вещества, диффундирующего сквозь единицу площади при единичном градиенте концентрации за единицу времени. (Источник: «Металлы и сплавы.… … Словарь металлургических терминов
коэффициент диффузии — difuzijos koeficientas statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, skaitine verte lygus difunduojančių dalelių srauto tankiui, kai jų tankio gradientas lygus 1. atitikmenys: angl. diffusion coefficient vok.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
коэффициент диффузии — difuzijos koeficientas statusas T sritis Standartizacija ir metrologija priedas( ai) Grafinis formatas atitikmenys: angl. diffusion coefficient vok. Diffusionskoeffizient, m; Diffusionskonstante, f rus. коэффициент диффузии, m pranc. coefficient… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
коэффициент диффузии — difuzijos koeficientas statusas T sritis chemija apibrėžtis Dydis, skaitine verte lygus medžiagos kiekiui, difunduojančiam per vienetinį laiką pro vienetinį plotą, kai koncentracijos gradientas lygus 1. atitikmenys: angl. diffusion coefficient… … Chemijos terminų aiškinamasis žodynas
коэффициент диффузии — rus коэффициент (м) диффузии (газов) eng gas transfer factor (lung) fra facteur (m) de transfert gazeux deu Gastransferfaktor (m) spa factor (m) de intercambio de gases, factor (m) de transferencia de gases … Безопасность и гигиена труда. Перевод на английский, французский, немецкий, испанский языки
коэффициент диффузии носителей заряда — коэффициент диффузии носителей заряда; коэффициент диффузии Абсолютная величина отношения плотности потока подвижных носителей заряда одного типа (т. е. электронов проводимости или дырок) к градиенту их концентрации в отсутствие электрического и… … Политехнический терминологический толковый словарь
Коэффициент диффузии
Содержание
В газах
с физическими величинами
Для самодиффузии (то есть в случае, если присутствует только один тип частиц) вышесказанное упрощается. Относится к:
В жидкостях
| материал | Коэффициент диффузии в м² / с |
|---|---|
| кислород | 2,1 × 10 −9 |
| серная кислота | 1,73 × 10 −9 |
| Этанол | 0,84 × 10 −9 |
Коэффициенты диффузии в жидкостях обычно составляют примерно одну десятитысячную от коэффициентов диффузии в газах. Они описываются уравнением Стокса-Эйнштейна :
Д. знак равно k Б. Т Шестой π η Р. 0 <\ Displaystyle D = <\ гидроразрыва <к _ <\ mathrm > \, T> <6 \, \ pi eta R_ <0>>>>
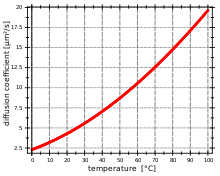
Поскольку вязкость растворителя является функцией температуры, зависимость коэффициента диффузии от температуры нелинейна.
В твердых телах
| система | Температура в ° C | Коэффициент диффузии в м² / с |
|---|---|---|
| Водород в железе | 10 | 1,66 × 10 −13 |
| 50 | 11,4 × 10 −13 | |
| 100 | 124 × 10 −13 | |
| Углерод в железе | 800 | 15 × 10 −13 |
| 1100 | 450 × 10 −13 | |
| Золото в свинце | 285 | 0,46 × 10 −13 |
Коэффициенты диффузии в твердых телах обычно в несколько тысяч раз меньше, чем коэффициенты диффузии в жидкостях.
D 0 можно приблизительно рассчитать как:
Однако рекомендуется определять коэффициенты диффузии в твердых телах, в частности, экспериментальным путем.
Эффективный коэффициент диффузии
Кажущийся коэффициент диффузии
Для линейной сорбции он рассчитывается следующим образом:
Коэффициент диффузии
Смотреть что такое «Коэффициент диффузии» в других словарях:
коэффициент диффузии — носителей заряда; коэффициент диффузии Абсолютная величина отношения плотности потока подвижных носителей заряда одного типа (т. е. электронов проводимости или дырок) к градиенту их концентрации в отсутствие электрического и магнитного полей.… … Политехнический терминологический толковый словарь
коэффициент диффузии — Коэффициент пропорциональности, представляющий количество вещества, диффундирующего сквозь единицу площади при единичном градиенте концентрации за единицу времени. [http://www.manual steel.ru/eng a.html] Тематики металлургия в целом EN diffusion… … Справочник технического переводчика
коэффициент диффузии — [diffusion constant] коэффициент пропорциональности в законах диффузии Фика (D, м2/с). По 1 му закону Фика dm/dс = DS(dC/dX), где m количество диффундируемого вещества, т время, S площадь, С концентрация, X направление диффузноного потока … Энциклопедический словарь по металлургии
Коэффициент диффузии — Коэффициент диффузии количественная характеристика скорости диффузии, равная количеству вещества (в массовых единицах), проходящего в единицу времени через участок единичной площади (например, 1 м²) при градиенте концентрации, равном… … Википедия
коэффициент диффузии — difuzijos koeficientas statusas T sritis fizika atitikmenys: angl. diffusion coefficient; diffusion constant; diffusivity vok. Diffusionskoeffizient, m; Diffusionskonstante, f rus. коэффициент диффузии, m; постоянная диффузии, f pranc.… … Fizikos terminų žodynas
коэффициент диффузии — difuzijos koeficientas statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, skaitine verte lygus difunduojančių dalelių srauto tankiui, kai jų tankio gradientas lygus 1. atitikmenys: angl. diffusion coefficient vok.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
коэффициент диффузии — difuzijos koeficientas statusas T sritis Standartizacija ir metrologija priedas( ai) Grafinis formatas atitikmenys: angl. diffusion coefficient vok. Diffusionskoeffizient, m; Diffusionskonstante, f rus. коэффициент диффузии, m pranc. coefficient… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
коэффициент диффузии — difuzijos koeficientas statusas T sritis chemija apibrėžtis Dydis, skaitine verte lygus medžiagos kiekiui, difunduojančiam per vienetinį laiką pro vienetinį plotą, kai koncentracijos gradientas lygus 1. atitikmenys: angl. diffusion coefficient… … Chemijos terminų aiškinamasis žodynas
коэффициент диффузии — rus коэффициент (м) диффузии (газов) eng gas transfer factor (lung) fra facteur (m) de transfert gazeux deu Gastransferfaktor (m) spa factor (m) de intercambio de gases, factor (m) de transferencia de gases … Безопасность и гигиена труда. Перевод на английский, французский, немецкий, испанский языки
коэффициент диффузии носителей заряда — коэффициент диффузии носителей заряда; коэффициент диффузии Абсолютная величина отношения плотности потока подвижных носителей заряда одного типа (т. е. электронов проводимости или дырок) к градиенту их концентрации в отсутствие электрического и… … Политехнический терминологический толковый словарь
Диффузия
Примером диффузии может служить перемешивание газов (например, распространение запахов) или жидкостей (если в воду капнуть чернил, то жидкость через некоторое время станет равномерно окрашенной). Другой пример связан с твёрдым телом: атомы соприкасающихся металлов перемешиваются на границе соприкосновения. Важную роль диффузия частиц играет в физике плазмы.
Обычно под диффузией понимают процессы, сопровождающиеся переносом материи, однако иногда диффузионными называют также другие процессы переноса: теплопроводность, вязкое трение и т. п.
Скорость протекания диффузии зависит от многих факторов. Так, в случае металлического стержня тепловая диффузия проходит очень быстро. Если же стержень изготовлен из синтетического материала, тепловая диффузия протекает медленно. Диффузия молекул в общем случае протекает ещё медленнее. Например, если кусочек сахара опустить на дно стакана с водой и воду не перемешивать, то пройдёт несколько недель, прежде чем раствор станет однородным. Ещё медленнее происходит диффузия одного твёрдого вещества в другое. Например, если медь покрыть золотом, то будет происходить диффузия золота в медь, но при нормальных условиях (комнатная температура и атмосферное давление) золотосодержащий слой достигнет толщины в несколько микронов только через несколько тысяч лет.
Количественно описание процессов диффузии было дано немецким физиологом А. Фиком (англ.) в 1855 г.
Содержание
Общее описание
Все виды диффузии подчиняются одинаковым законам. Скорость диффузии пропорциональна площади поперечного сечения образца, а также разности концентраций, температур или зарядов (в случае относительно небольших величин этих параметров). Так, тепло будет в четыре раза быстрее распространяться через стержень диаметром в два сантиметра, чем через стержень диаметром в один сантиметр. Это тепло будет распространяться быстрее, если перепад температур на одном сантиметре будет 10 °C вместо 5 °C. Скорость диффузии пропорциональна также параметру, характеризующему конкретный материал. В случае тепловой диффузии этот параметр называется теплопроводность, в случае потока электрических зарядов — электропроводность. Количество вещества, которое диффундирует в течение определённого времени, и расстояние, проходимое диффундирующим веществом, пропорциональны квадратному корню времени диффузии.
Диффузия представляет собой процесс на молекулярном уровне и определяется случайным характером движения отдельных молекул. Скорость диффузии в связи с этим пропорциональна средней скорости молекул. В случае газов средняя скорость малых молекул больше, а именно она обратно пропорциональна квадратному корню из массы молекулы и растёт с повышением температуры. Диффузионные процессы в твёрдых телах при высоких температурах часто находят практическое применение. Например, в определённых типах электронно-лучевых трубок (ЭЛТ) применяется металлический торий, продиффундировавший через металлический вольфрам при 2000 °C.
Если в смеси газов масса одной молекулы в четыре раза больше другой, то такая молекула передвигается в два раза медленнее по сравнению с её движением в чистом газе. Соответственно, скорость диффузии её также ниже. Эта разница в скорости диффузии лёгких и тяжёлых молекул применяется, чтобы разделять субстанции с различными молекулярными весами. В качестве примера можно привести разделение изотопов. Если газ, содержащий два изотопа, пропускать через пористую мембрану, более лёгкие изотопы проникают через мембрану быстрее, чем тяжёлые. Для лучшего разделения процесс производится в несколько этапов. Этот процесс широко применялся для разделения изотопов урана (отделение 235 U от основной массы 238 U). Поскольку такой способ разделения требует больших энергетических затрат, были развиты другие, более экономичные способы разделения. Например, широко развито применение термодиффузии в газовой среде. Газ, содержащий смесь изотопов, помещается в камеру, в которой поддерживается пространственный перепад (градиент) температур. При этом тяжёлые изотопы со временем концентрируются в холодной области.
Уравнения Фика
С точки зрения термодинамики движущим потенциалом любого выравнивающего процесса является рост энтропии. При постоянных давлении и температуре в роли такого потенциала выступает химический потенциал µ, обуславливающий поддержание потоков вещества. Поток частиц вещества пропорционален при этом градиенту потенциала
В большинстве практических случаев вместо химического потенциала применяется концентрация C. Прямая замена µ на C становится некорректной в случае больших концентраций, так как химический потенциал перестаёт быть связан с концентрацией по логарифмическому закону. Если не рассматривать такие случаи, то вышеприведённую формулу можно заменить на следующую:
которая показывает, что плотность потока вещества J [

Коэффициент диффузии D зависит от температуры. В ряде случаев в широком интервале температур эта зависимость представляет собой уравнение Аррениуса.
Дополнительное поле, наложенное параллельно градиенту химического потенциала, нарушает стационарное состояние. В этом случае диффузионные процессы описываются нелинейным уравнением Фоккера—Планка. Процессы диффузии имеют большое значение в природе:
Геометрическое описание уравнения Фика
Во втором уравнении Фика в левой части стоит скорость изменения концентрации во времени, а в правой части уравнения — вторая частная производная, которая выражает пространственное распределение концентрации, в частности, выпуклость функции распределения температур, проецируемую на ось х.
Диффузия
Вы будете перенаправлены на Автор24
Что такое диффузия и коэффициент диффузии
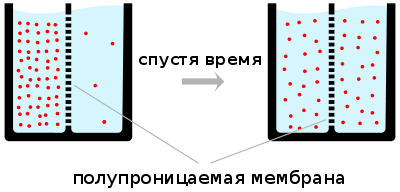
Диффузией называется обусловленное тепловым движением выравнивание концентраций в смеси нескольких веществ.
Этот процесс наблюдается в газообразных, жидких и твердых средах. Пpи диффузии газов речь идет о проникновении одного газа в другой за счет теплового движения. Пpи диффузии переносится масса некоторого компонента в смеси газов. Опыт показывает, что плотность потока диффузии (число диффундирующих молекул в секунду через единичную площадку, ориентированную перпендикулярно потоку диффузии) пропорциональна градиенту молекулярной плотности данного компонента смеси. То есть:
Вследствие теплового движения возникает поток молекул каждой компоненты в направлении убывания ее концентрации. Экспериментально установлено, что поток молекул i- ой компоненты через перпендикулярную к оси Ox поверхность S определяется уравнением:
Получим коэффициент диффузии, исходя из представлений МКТ о явлениях переноса в газах. Рассмотрим двухкомпонентную смесь. Будем предполагать, что молекулы газа движутся только в трех взаимно перпендикулярных направлениях. Отступая от единичной площадки М на длину свободного пробега вправо и влево, построим куб единичного объема. В среднем одна шестая часть молекул этих кубиков летит по направлению к площадке. В соответствии с этим количество молекул, пролетающих через единичную воображаемую площадку в единицу времени:
\[\nu =\frac<1><6>n\left\langle v\right\rangle \ \left(4\right),\]
При небольших нарушениях процессов равновесия считаем, что:
\[\lambda =\frac<1><\sqrt<2>\sigma n>,\ n=n_1+n_2\left(5\right).\]
Чем реже сталкиваются молекулы, и чем выше их скорость, тем диффузия проходит интенсивнее, поэтому запишем:
\[D\sim \left\langle v\right\rangle \lambda \left(6\right).\]
\[N’_1=\frac<1><6>n’_1\left\langle v\right\rangle S,N’_2=\frac<1><6>n’_2\left\langle v\right\rangle S\ \left(7\right),\]
\[n’_1=n_1\left(x-л\right),\ n’_2=n_2\left(x+\lambda \right)\left(8\right).\]
Используем формулу (7):
\[N_1=-\left(\frac<1><3>\left\langle v\right\rangle \lambda \right)\frac
Так, мы получили уравнение диффузии для первой компоненты, кроме того, сравнив (11) с (2), получим:
\[D=\frac<1><3>\left\langle v\right\rangle \lambda \ \left(12\right).\]
Так как мы предположили, что массы молекул обеих компонент по массе и эффективному сечению равны, то, вообще говоря, мы имеем дело с самодиффузией (диффузией молекул газа между молекулами того же газа).
Запишем уравнение плотности потока концентрации:
\[D=\frac<1><6>\left\langle \lambda \right\rangle \left\langle v\right\rangle \to j_d=-\frac<1><6>\left\langle \lambda \right\rangle \left\langle v\right\rangle \frac
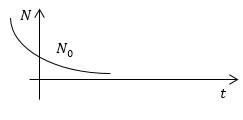
Изобразим график закона изменения числа молекул в сосуде.
Ответ: Закон изменения числа молекул в сосуде N(t)=$\ Ce^<-\frac<1><6>\frac<\left\langle v\right\rangle >
Готовые работы на аналогичную тему
Задание: Найдите коэффициент диффузии D воздуха при давлении p и температуре T. Диаметр молекулы воздуха d.
Запишем выражение для коэффициента диффузии:
\[D=\frac<1><3>\left\langle v\right\rangle \lambda \left(2.1\right),\]
Из основного уравнения МКТ (p=nkT), имеем:
Используем (2.2) и (2.5), подставим в (2.1), получим:
Ответ: Коэффициент диффузии воздуха D$=\frac<1><3>\sqrt<\frac<8RT><\pi \mu>>\frac