что такое код фибоначчи

5 способов вычисления чисел Фибоначчи: реализация и сравнение

Введение

Программистам числа Фибоначчи должны уже поднадоесть. Примеры их вычисления используются везде. Всё от того, что эти числа предоставляют простейший пример рекурсии. А ещё они являются хорошим примером динамического программирования. Но надо ли вычислять их так в реальном проекте? Не надо. Ни рекурсия, ни динамическое программирование не являются идеальными вариантами. И не замкнутая формула, использующая числа с плавающей запятой. Сейчас я расскажу, как правильно. Но сначала пройдёмся по всем известным вариантам решения.

Код предназначен для Python 3, хотя должен идти и на Python 2.

Для начала – напомню определение:

Замкнутая формула

Решаем квадратное уравнение:

Откуда и растёт «золотое сечение» ϕ=(1+√5)/2. Подставив исходные значения и проделав ещё вычисления, мы получаем:

что и используем для вычисления F_n.

Хорошее:
Быстро и просто для малых n
Плохое:
Требуются операции с плавающей запятой. Для больших n потребуется большая точность.
Злое:
Использование комплексных чисел для вычисления F_n красиво с математической точки зрения, но уродливо — с компьютерной.

Рекурсия

Самое очевидное решение, которое вы уже много раз видели – скорее всего, в качестве примера того, что такое рекурсия. Повторю его ещё раз, для полноты. В Python её можно записать в одну строку:

Хорошее:
Очень простая реализация, повторяющая математическое определение
Плохое:
Экспоненциальное время выполнения. Для больших n очень медленно
Злое:
Переполнение стека

Запоминание

У решения с рекурсией есть большая проблема: пересекающиеся вычисления. Когда вызывается fib(n), то подсчитываются fib(n-1) и fib(n-2). Но когда считается fib(n-1), она снова независимо подсчитает fib(n-2) – то есть, fib(n-2) подсчитается дважды. Если продолжить рассуждения, будет видно, что fib(n-3) будет подсчитана трижды, и т.д. Слишком много пересечений.

Поэтому надо просто запоминать результаты, чтобы не подсчитывать их снова. Время и память у этого решения расходуются линейным образом. В решении я использую словарь, но можно было бы использовать и простой массив.

(В Python это можно также сделать при помощи декоратора, functools.lru_cache.)

Хорошее:
Просто превратить рекурсию в решение с запоминанием. Превращает экспоненциальное время выполнение в линейное, для чего тратит больше памяти.
Плохое:
Тратит много памяти
Злое:
Возможно переполнение стека, как и у рекурсии

Динамическое программирование

После решения с запоминанием становится понятно, что нам нужны не все предыдущие результаты, а только два последних. Кроме этого, вместо того, чтобы начинать с fib(n) и идти назад, можно начать с fib(0) и идти вперёд. У следующего кода линейное время выполнение, а использование памяти – фиксированное. На практике скорость решения будет ещё выше, поскольку тут отсутствуют рекурсивные вызовы функций и связанная с этим работа. И код выглядит проще.

Это решение часто приводится в качестве примера динамического программирования.

Хорошее:
Быстро работает для малых n, простой код
Плохое:
Всё ещё линейное время выполнения
Злое:
Да особо ничего.

Матричная алгебра

И, наконец, наименее освещаемое, но наиболее правильное решение, грамотно использующее как время, так и память. Его также можно расширить на любую гомогенную линейную последовательность. Идея в использовании матриц. Достаточно просто видеть, что

А обобщение этого говорит о том, что

Два значения для x, полученных нами ранее, из которых одно представляло собою золотое сечение, являются собственными значениями матрицы. Поэтому, ещё одним способом вывода замкнутой формулы является использование матричного уравнения и линейной алгебры.

Так чем же полезна такая формулировка? Тем, что возведение в степень можно произвести за логарифмическое время. Это делается через возведения в квадрат. Суть в том, что

где первое выражение используется для чётных A, второе для нечётных. Осталось только организовать перемножения матриц, и всё готово. Получается следующий код. Я организовал рекурсивную реализацию pow, поскольку её проще понять. Итеративную версию смотрите тут.

Хорошее:
Фиксированный объём памяти, логарифмическое время
Плохое:
Код посложнее
Злое:
Приходится работать с матрицами, хотя они не так уж и плохи

Сравнение быстродействия

Сравнивать стоит только вариант динамического программирования и матрицы. Если сравнивать их по количеству знаков в числе n, то получится, что матричное решение линейно, а решение с динамическим программированием – экспоненциально. Практический пример – вычисление fib(10 ** 6), числа, у которого будет больше двухсот тысяч знаков.

n = 10 ** 6
Вычисляем fib_matrix: у fib(n) всего 208988 цифр, расчёт занял 0.24993 секунд.
Вычисляем fib_dynamic: у fib(n) всего 208988 цифр, расчёт занял 11.83377 секунд.

Теоретические замечания

Не напрямую касаясь приведённого выше кода, данное замечание всё-таки имеет определённый интерес. Рассмотрим следующий граф:

Подсчитаем количество путей длины n от A до B. Например, для n = 1 у нас есть один путь, 1. Для n = 2 у нас опять есть один путь, 01. Для n = 3 у нас есть два пути, 001 и 101. Довольно просто можно показать, что количество путей длины n от А до В равно в точности F_n. Записав матрицу смежности для графа, мы получим такую же матрицу, которая была описана выше. Это известный результат из теории графов, что при заданной матрице смежности А, вхождения в А n — это количество путей длины n в графе (одна из задач, упоминавшихся в фильме «Умница Уилл Хантинг»).

Почему на рёбрах стоят такие обозначения? Оказывается, что при рассмотрении бесконечной последовательности символов на бесконечной в обе стороны последовательности путей на графе, вы получите нечто под названием «подсдвиги конечного типа», представляющее собой тип системы символической динамики. Конкретно этот подсдвиг конечного типа известен, как «сдвиг золотого сечения», и задаётся набором «запрещённых слов» <11>. Иными словами, мы получим бесконечные в обе стороны двоичные последовательности и никакие пары из них не будут смежными. Топологическая энтропия этой динамической системы равна золотому сечению ϕ. Интересно, как это число периодически появляется в разных областях математики.

Источник

Что такое числа Фибоначчи и почему их выделили в отдельную группу чисел?

Числа Фибоначчи в Европе популяризовал Леонардо Пизанский (по прозвищу Фибоначчи – сын Боначчи), в задаче о кроликах:

Пусть в огороженном месте имеется пара кроликов (самка и самец) в первый день января. Эта пара кроликов производит новую пару кроликов (самку и самца) в первый день февраля и затем в первый день каждого следующего месяца. Каждая новорожденная пара кроликов становится зрелой уже через месяц и затем через месяц дает жизнь новой паре кроликов. Возникает вопрос: сколько пар кроликов будет в огороженном месте через год, то есть через 12 месяцев с начала размножения.

Оказывается, число кроликов по месяцам описывается последовательностью

В ней каждое число равно сумме двух предыдущих. Условия задачи все равно нереалистичны, так что можно не стесняться: предположить, что кролики бессмертны, и продолжить последовательность до бесконечности:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269, 2178309, 3524578, 5702887, 9227465, 14930352, 24157817, 39088169, 63245986, 102334155, ….

Есть свидетельства, что последовательность задолго до Леонардо была известна в Индии, и что в честь Фибоначчи ее назвал Эдуард Люка.

Про экспоненциальный рост

Как мы видим, последовательность очень быстро растет (экспоненциально, как последовательность степеней). Примерно как 1, 2, 4, 8, 16, 32, … или 1, 10, 100, 1000, … (тоже экспоненциальный рост.) Экспоненциальный рост вообще встречается в природе и в приложениях: так растут популяции, капиталы в банке, число радиоактивных атомов и число зерен на шахматной доске (Вы же помните легенду про жадного султана и бедного изобретателя шахмат ;))

В природе экспоненциальный рост имеет место лишь приблизительно и только в некоторых пределах.

Красивые фотографии

Последовательности в природе, напоминающие Фибоначчи, тоже похожи на Фибоначчи только приблизительно и в некоторых пределах. Широко известны примеры из мира растений: семена подсолнуха, сосновые шишки, лепестки цветков, ячейки ананаса. Видимо, здесь задействован один механизм (я скопировала первую попавшуюся картинку из интернета):

Отчасти популярность чисел Фибоначчи связана с такими красивыми картинками. В интернете их полным-полно.

А вот скажем, закон радиоактивного распада не менее поразителен, история его открытия драматична, человечество поставило его себе на службу… но он не так популярен в СМИ. Нет для него таких красивых картинок, да и описывается он дифференциальным уравнением, а любителей дифференциальных уравнений меньше, чем любителей красивых картинок.

В математике

В математике бывают объекты, которые задаются очень просто, но показывают удивительно сложные и многогранные связи между своими компонентами. Например: треугольник в планиметрии, конические сечения, треугольник Паскаля, простые числа, … Они завораживают нас как картинки в калейдоскопе. Чуть повернешь – и открываются новые узоры, новые свойства. Числа Фибоначчи –один из таких объектов. Каждый математик на пути в науку их обязательно встречал.

Чтобы перечислить все их удивительные свойства, нужна отдельная книга (и кстати, выходит журнал с таким названием, посвященный одним только числам Фибоначчи). Скажу только, что отношение каждого числа Фибоначчи к предыдущему приближает золотое сечение, и чем числа больше, тем приближение лучше.

Почему же математики выделили числа Фибоначчи в отдельную группу чисел

Специалист по теории чисел Леопольд Кронекер считал, что только одна из них создана Богом (и это вовсе не последовательность Фибоначчи, а другая, на сайте ее номер 27), а остальные – дело рук человеческих.

В целом журналисты несколько преувеличивают значимость чисел Фибоначчи: они, безусловно, прекрасны, но стоят в одном ряду с многими другими не менее прекрасными и полезными математическими объектами.

Источник

Число Фибоначчи. Почему оно так популярно в природе?

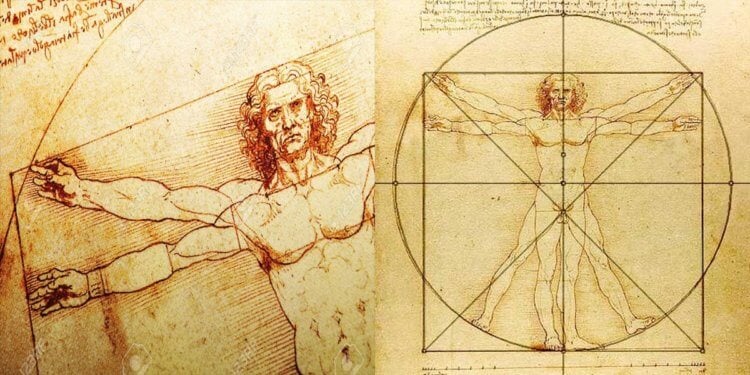
Таинственное число Фибоначчи, равное 1,618, будоражит умы ученых уже на протяжении нескольких тысячелетий. Кто-то считает это число строителем мироздания, кто-то называет его числом Бога, а кто-то, не мудрствуя лукаво, просто применяет его на практике и получает невероятные архитектурные, художественные и математические творения. Число Фибоначчи было обнаружено даже в пропорциях знаменитого «Витрувианского человека» Леонардо Да Винчи, который утверждал, что знаменитое число, пришедшее из математики, руководит всей Вселенной.

«Витрувианский человек» Леонардо да Винчи обладает идеальными пропорциями, основанными на знании свойств числа Фибоначчи

Кто такой Фибоначчи?

Леонардо Пизанский считается самым первым крупным математиком в истории средневековой Европы. Несмотря на это, свое знаменитое прозвище «Фибоначчи» ученый получил далеко не из-за своих экстраординарных математических способностей, но из-за своего везения, так как «боначчи» по-итальянски означает «удачливый». Перед тем как стать одним из самых известных математиков раннего Средневековья, Леонардо Пизанский изучал точные науки у самых продвинутых учителей своего времени, которыми считались арабы. Именно благодаря этой деятельности Фибоначчи, в Европе появились десятичная система счисления и арабские цифры, которыми мы пользуемся до сих пор.

В одном из своих самых известных трудов под названием «Liber abaci», Леонардо Пизанский приводит уникальную закономерность чисел, которые при постановке в ряд образуют линию цифр, каждая из которых является суммой двух предыдущих чисел.

Последовательность Фибоначчи

Иными словами, последовательность Фибоначчи выглядит так:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 и так далее.

Каждое число из ряда Фибоначчи, разделенное на последующее, имеет значение, стремящееся к уникальному показателю, которое составляет 1,618. Первые числа ряда Фибоначчи не дают настолько точное значение, однако по мере нарастания, соотношение постепенно выравнивается и становится все более точным.

Леонардо Пизанский — тот самый создатель числа Фибоначчи

Где используется число Фибоначчи

Из-за своего повсеместного применения в природе, золотое сечение (именно так число Фибоначчи иногда называют в искусстве и математике) считается одним из самых гармонизирующих законов мироздания, который упорядочивает структуру окружающего нас мира и направляет жизнь на развитие. Так, правило золотого сечения применяется природой для образования траекторий движения вихревых потоков в ураганах, при образовании эллиптических галактик, к которым относится и наш Млечный Путь, при «строительстве» раковины улитки или ушной раковины человека, направляет движение косяка рыб и показывает траекторию движения испуганной стаи оленей, врассыпную убегающую от хищника.

Проявление золотого сечения в природе

Эстетичность такой гармонизации мироздания воспринимается человеком, который всегда стремился улучшить окружающую его действительность, в качестве стабилизирующего природу закона. Находя золотое сечение в лице того или иного человека, мы инстинктивно воспринимаем собеседника в качестве гармоничной личности, чье развитие происходит без сбоев и нарушений. Этим можно объяснить то, почему иногда нам по непонятным причинам больше нравится одно лицо, чем другое. Оказывается, о наших возможных симпатиях позаботилась природа!

Как вы считаете, является ли повсеместное применение числа Фибоначчи в природе совпадением или свидетельством наличия некоего вселенского разума? Давайте попробуем обсудить этот вопрос в нашем Telegram-чате.

Наиболее распространенное определение золотого сечения гласит, что меньшая часть так относится к большей, как большая часть относится ко всему целому. Уникальное правило встречается во всех областях природы, науки и искусства, позволив некоторым именитым исследователям Средних Веков сделать предположение, что три основные части золотого сечения олицетворяют собой христианских Отца, Сына и Святого Духа.

Правилу золотого сечения следуют даже галактики. Наш Млечный Путь в этом плане не является исключением

Что такое золотое сечение

С точки зрения математики, золотое сечение представляет собой некую идеальную пропорцию, к которой каким-то образом стремится все живое и неживое в природе.

Так выглядит «золотое сечение»

Используя основные принципы ряда Фибоначчи, растут семечки в центре подсолнуха, движется спираль ДНК, был построен Парфенон и написана самая знаменитая картина в мире — «Джоконда» Леонардо Да Винчи.

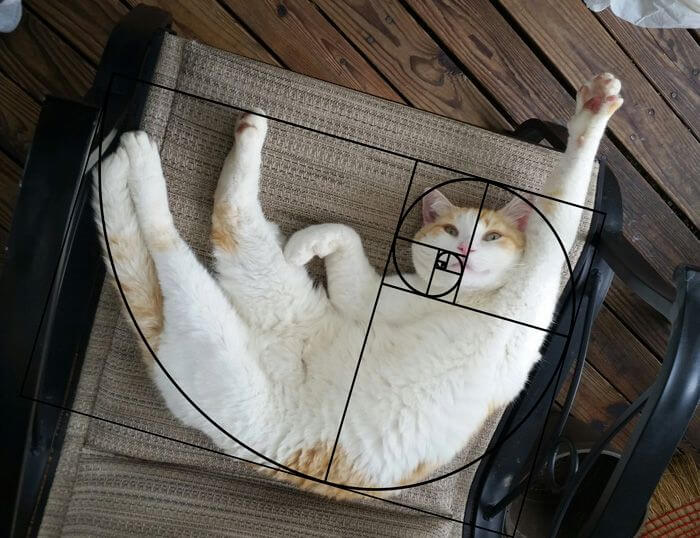
Даже коты неосознанно (хотя, кто знает?) следуют принципу золотого сечения, становясь любимцами большей части населения планеты

Есть ли в природе гармония? Несомненно, есть. А ее доказательством служит число Фибоначчи, происхождение которого нам еще только предстоит отыскать.

Новости, статьи и анонсы публикаций

Свободное общение и обсуждение материалов

Когда мы смотрим на Вселенную, довольно трудно представить, что это вот все — планеты, звезды, галактики, сложные жизни, которыми мы наслаждаемся, — все возн…

Муравьи считаются одними из самых успешных созданий на нашей планете. Ведь какой еще вид живых существ может похвастаться тем, что они есть практически в каж…

Ученые нашли способ управлять хищными растениями при помощи смартфона и нескольких электродов. 🥀 Они подключили к питающейся насекомыми мухоловке два провода и сделали так, чтобы растение закрывало свою «пасть» строго по их приказу. На видео показано, для чего это нужно.

Источник

masterok

Мастерок.жж.рф

Хочу все знать

Итак, мы выяснили с вами Кто такой Фибоначчи, а теперь давайте рассмотрим вот такой феномен.

Оказывается Фибоначчи повсюду!

На самом деле эти числа были известны задолго до Фибоначчи ещё в древней Индии, где они использовались в метрическом стихосложении.

Леонардо Фибоначчи первым ввёл эту числовую последовательность в западноевропейской математической науке в своей важной книге «Liber Abaci» («Книга абака») в 1202 году. Он использовал эту последовательность чисел, когда пытался объяснить рост популяции кроликов.

Фибоначчи рассматривает гипотетическую ситуацию, когда в поле появляется пара кроликов. Они спариваются в конце месяца и в конце второго месяца самка производит еще одну пару. Кролики никогда не умирают, спариваются ровно через месяц, и самки всегда производят пару (один самец, одна самка). Вопрос, который поставил Фибоначчи был следующим: сколько пар будет через один год? Если посчитать, то окажется, что количество пар в конце N-го месяца равно Fn или N-му числу Фибоначчи. Таким образом, количество пар кроликов через 12 месяцев будет F12 или 144.

Числа Фибоначчи и золотое сечение

Как известно, последовательность Фибоначчи начинается с 1 и 1, после чего каждое новое число является результатом сложения двух предыдущих чисел:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …

Если разделить два последовательных числа в этом ряду, например 144/89, в конечном итоге получится число 1,618, которое называется «Золотое число» или «Золотое сечение».

Последовательное приближение соотношения двух соседних чисел ряда Фибоначчи к Золотому сечению.

Пропорция золотого сечения считается эстетически приятной и из-за этого многие художники и архитекторы, в том числе Сальвадор Дали и Ле Корбюзье использовали её в своих работах.
Последовательность Фибоначчи и Золотое сечение тесно взаимосвязаны. Отношение последовательных чисел Фибоначчи сходится и приближается к золотому сечению, а выражение замкнутой формулы для последовательности Фибоначчи включает Золотое сечение.

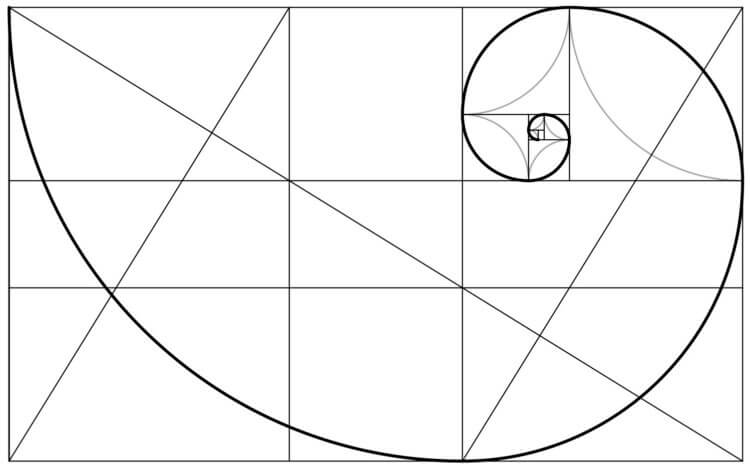
Золотой прямоугольник (розовый) с длинной стороной a и короткой стороной b, и находящийся рядом с ним квадрат со стороной длиной a, создадут подобный золотой прямоугольник с длинной стороной а + b и короткой стороной a. Это изобажение иллюстрирует взаимосвязь отношений (a+b)/a = a/b.

Спираль Фибоначчи или золотая спираль — это последовательность соединенных четвертей окружностей, вписанных внутри массивов квадратов со сторонами равными числам Фибоначчи. Квадраты идеально подходят друг к другу из-за природы последовательности Фибоначчи, в которой следующее число равно сумме двух перед ним (см.предыдущий рисунок). Любые два последовательных числа Фибоначчи имеют отношение, очень близкое к золотому сечению, которое составляет примерно 1.618034. Чем больше пара чисел Фибоначчи, тем ближе это приближение. Спираль и результирующий прямоугольник называются золотым прямоугольником.

Почему эта последовательность настолько уникальна
Числа Фибоначчи описывают различные явления в искусстве, музыке и природе. Числа спиралей на большинстве шишек и ананасах равны числам Фибоначчи. Расположение листьев и ветвей на стеблях многих растений соответствуют числам Фибоначчи. На пианино количество белых (8) клавиш и черных (5) клавиш в каждой октаве (13) являются числами Фибоначчи. Длины и ширины много прямоугольных предметов, таких как учетные карточки, окна, игральные карты и пр. соответствуют последовательным числам ряда Фибоначчи.

Числа Фибоначчи в природе

Подсолнухи являются отличными примерами последовательности Фибоначчи, потому что семена в центре цветка организованы в два набора спиралей — короткие, идущие по часовой стрелке от центра, и более длинные — против часовой стрелки. Если считать спирали последовательно, то, видимо, всегда найдутся числа Фибоначчи.

Вот еще несколько примеров, где вы можете найти спираль Фибоначчи в природе.

Неудивительно, что спиральные галактики также следуют знакомой схеме Фибоначчи. Млечный Путь имеет несколько спиральных рукавов, каждый из которых представляет логарифмическую спираль около 12 градусов.

Числа Фибоначчи в теле человека

Есть много примеров соотношений частей тела человека на основе последовательности Фибоначчи, например рука и, в частности, кости пальца.

Каждая кость указательного пальца, от кончика до основания запястья, больше предыдущей примерно на коэффициент Фибоначчи 1,618, что соответствует числам Фибоначчи 2, 3, 5 и 8.

Числа Фибоначчи в биржевой торговле

Последовательность Фибоначчи является инструментом технического анализа, используемым профессиональными трейдерами в сочетании с другими инструментами для расчета прогноза потенциального конца коррекции, принимая процент от предыдущего движения.

Считается, что во время мощного рыночного движения, цены могут откатываться на 23,6% (это соответствует отношению числа ряда Фибоначчи на позиции N к числу на позиции N+3), 38,2% (соответствует отношению числа ряда Фибоначчи на позиции N к числу на позиции N+2) или 50% (половина). Эти уровни коррекции Фибоначчи считаются «нормальными». Если же цена падает на 61,2% (отношение двух соседних чисел ряда Фибоначчи — позиции N и N+1) и более, то это серьезный сигнал вероятного разворота тренда.

Числа Фибоначчи в фотографии и искусстве

В фотографии сетка фи (phi) является интерполяцией спирали Фибоначчи и в наши дни считается фундаментальным методом для создания приятной композиции в кадре. Цель состоит в том, чтобы выровнять объект по линиям, созданным спиралью, или использовать её в качестве разделителя для создания правильного ощущения кадра.

Сетка фи (красные линии) и спираль Фиббоначи в кадре.

Имеется много примеров, когда последовательность Фибоначчи появляется вокруг нас, и мы не обращаем внимания на это математическое чудо, которое кажется таинственным фактором, приносящим универсальную форму гармонии элементам математического музыкального искусства природы.

Может именно из-за этого Дональд Трамп был избран президентом? (шутка):

И еще немного фундаментального числа!

Источник

Как я посчитал миллионное число Фибоначчи

Все мы понимаем, что рекурсивное вычисление чисел Фибоначчи крайне неэффективно. Многим людям наверняка хотелось проверить, где пределы (не)эффективности, но не доходили руки, не хватало времени. Специально к старту нового потока курса Fullstack-разработчик на Python мы решили поделиться переводом статьи, автор которой шаг за шагом показывает возможности современного Python на примере разных подходов к вычислению чисел Фибоначчи. В статье вы найдёте проблемные значения n и сравнение производительности оптимального и неоптимального решений на графике.

Нет, заголовок вообще не кликбейтный. Несколько дней назад я действительно хотел найти оптимальное решение для расчёта чисел Фибоначчи, хотелось попробовать вычислить стотысячное число последовательности, но я задумался; если я могу вычислить стотысячное число, то что остановит меня в поисках миллионного числа Фибоначчи? Сегодня я покажу, как шёл к вычислению и с какими проблемами столкнулся.

Последовательность Фибоначчи — одна из наиболее известных математических последовательностей и самый простой пример рекуррентных отношений. Каждое число последовательности — это сумма двух предыдущих чисел, начиная с 0 и 1. Получается такая последовательность:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и так далее.

В следующие несколько минут я исследую несколько разных подходов, а затем покажу оптимальное решение:

Расчёт 1000000-го числа Фибоначчи.

Но, прежде чем мы начнём, я должен сказать, что все упомянутые тайминги касаются оборудования, на котором я работаю сейчас, а версия Python — 3.9.1.

Простая рекурсия

Это очень простой способ получить N-ное число Фибоначчи на Python:

В коде используется рекурсия, он вызывает сам себя несколько раз, вычисляя предыдущее число и используя это число для вычисления следующего. Но это также недостаток, поскольку функция чрезвычайно неэффективна и ресурсоёмка: на каждом этапе она вычисляет предыдущие 2 числа, а также предыдущие 2 числа этих чисел и т. д.

Вскоре вы достигаете точки, когда вычисление следующего числа занимает слишком много времени, например, на моём компьютере мне потребовалось 1,43 секунды, чтобы вычислить 35-е число. Очевидно, что вычисление более высоких значений будет чрезвычайно медленным и практически невозможным.

Кеш с рекурсией

Поскольку мы постоянно вычисляем предыдущие 2 числа, для хранения числа можно воспользоваться возможностями кеширования, не нужно будет вычислять числа несколько раз. Встроенный модуль functools позволяет нам работать с LRU кешем; этот тип кеша организует элементы в порядке их использования. Такой подход может значительно ускорить процесс.

Во-первых, нам нужно импортировать декоратор lru_cache из модуля functools и поместить его перед нашей функцией. Мы можем указать значение maxsize, чтобы сообщить кешу, сколько элементов нужно хранить, но по умолчанию оно равно 128, это значение прекрасно работает. Используя кеш, мы можем вычислить 200-е число Фибоначчи всего за 0,0002252 секунды!

Одна проблема с использованием рекурсии заключается в том, что если вы попытаетесь вычислить 501-е число, то получите ошибку RecursionError: maximum recursion depth exceeded in comparison. Но, к счастью, проблему можно решить, установив большее значение глубины рекурсии:

Теперь мы можем вычислить 1000-е число Фибоначчи, на вычисление которого мне потребовалось всего 0,001198 секунды. Однако это создало для меня ещё одну проблему: по какой-то странной причине я не мог вычислить 1553-е число в последовательности, и даже после увеличения предела рекурсии ничего не произойдёт, ничего не будет распечатано на терминале, и программа просто закончит выполнение. Очевидно, что это проблема и недостаток на моём пути к вычислению миллионного числа Фибоначчи.

Итеративный метод

Вы можете увидеть, что применение рекурсивного решения проблемы в компьютерной науке часто рассматривается как халатность, а итеративные методы считаются намного лучше. Для генерации чисел Фибоначчи мы можем создать итеративное решение:

Мы можем воспользоваться им, чтобы вычислить любое число Фибоначчи (я не тестировал подход с особенно большими числами), и часто этот подход работает также очень быстро, 1000-е число вычислилось всего за 0,0028195 секунды.

Вы можете задаться вопросом, почему нельзя воспользоваться этим подходом для вычисления 1000000-го числа, и да, это возможно, но займёт немного времени. Продолжайте читать, и я расскажу, почему.

Формула Бине

Формула Бине — это формула, которая может использоваться для вычисления n-го члена последовательности Фибоначчи, а это именно то, что мы хотим сделать; эта формула названа в честь открывшего её французского математика Жака Филиппа Мари Бине. Вот она:

Формула Бине для вычисления n-ного числа Fibonacci

Вы можете заметить греческую букву PHI (ϕ), она означает золотое сечение:

Уравнение золотого сечения, phi

Можно написать формулу на Python и сразу же начать работать с ней:

Примечание: для реализации на Python нам нужно вернуть округление вычисляемого числа, потому что при вычислении большого числа Python вернёт результат, в котором может быть более двадцати девяток после запятой.

Всё это хорошо, так как теперь у нас нет никаких циклов и мы можем мгновенно вычислить ответ, верно? Что ж, в этом методе есть небольшая загвоздка. Если мы попытаемся вычислить что-либо выше 1475-го числа, то столкнёмся с ошибкой: OverflowError: (34, result too large). Это связано с тем, как в python реализованы числа с плавающей точкой, они могут иметь конкретное максимальное значение, которое мы превышаем, когда используем этот метод.

Однако исправить ситуацию очень легко. Мы можем использовать встроенный модуль под названием decimal, чтобы создать десятичный объект с гораздо более высокой точностью и подходящим для работы с уравнением размером:

В этой новой функции мы устанавливаем значение точности длиной 10000 цифр, преобразуем наше значение квадратного корня из 5 в десятичное значение объекта и используем его в нашем уравнении. Это позволяет нам легко вычислить 10000-е число в последовательности за поразительные 0,0692986 секунды, а это по сравнению со всеми нашими предыдущими методами огромное улучшение.

Расчёт 1000000-го числа Фибоначчи

Теперь вы, возможно, заметили, что формула работает медленнее итерационного решения, когда n=10000. Это связано с тем, что в формуле нам нужно создать десятичный объект и использовать его в уравнении, этот процесс занимает больше времени, чем повторение одной простой инструкции 10000 раз. Но история ещё не окончена.

Увеличение количества циклов может радикально увеличить длительность всего процесса. В какой-то момент, когда n составляет приблизительно 89200, время, необходимое итеративному решению для вычисления ответа, равно времени, которое необходимо при вычислении по формуле; когда же n увеличивается, время выполнения итеративного алгоритма возрастает с большей скоростью, чем время на решение по формуле.

График, показывающий время работы формулы Бине и итерационного решения

На графике видно точку пересечения времени выполнения формулы и итерационных графиков. Исходя из этого мы можем сказать, что с увеличением n время вычисления числа Фибоначчи по формуле возрастает линейно. Но при итеративном решении время увеличивается с увеличением n. Это даёт нам понять, что для вычисления миллионного числа Фибоначчи нам нужно использовать формулу. Дополнительное изменение, которое я должен был сделать, чтобы правильно вычислить число, — увеличить точность моего десятичного объекта строкой кода decimal.getcontext().prec = 300000.

Ваше время выполнения алгоритма может отличаться. На моём компьютере, чтобы вычислить 1000000-е число Фибоначчи, потребовалось:

8,832661 секунды при решении с итерацией;

1,151380 секунды с формулой Бине, это в 7,7 раза быстрее!

Если вам хочется узнать число, оно состоит из 208988 цифр и в текстовом файле занимает 209 КБ:

Заключение

Вот так я вычислил миллионное число Фибоначчи, конечно, я мог бы вычислить число больше, но на самом деле для этого нет никакой реальной причины, и это заняло бы много времени, даже с использованием формулы Бине. Из приведённого выше графика я могу оценить затраты времени: чтобы вычислить миллиардное число Фибоначчи, мне потребуется примерно 310,8467 секунды, я оставлю это читателям. А чтобы получить специальность Fullstack-разработчик на Python — потребуется немногим более года. Но можно и быстрее — на нашем курсе студенты не привязаны к программе и скорость их прогресса зависит от них самих.

Узнайте, как прокачаться и в других специальностях или освоить их с нуля:

Источник