что такое клика в графе

Клика (теория графов)

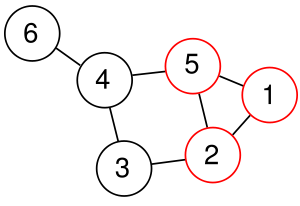
Клика — полный подграф неориентированного графа. Другими словами, клика графа есть подмножество его вершин, такое, что между каждой парой вершин этого подмножества существует ребро и, кроме того, это подмножество не принадлежит никакому большему подмножеству с тем же свойством.

См. также

Смотреть что такое «Клика (теория графов)» в других словарях:

Дуга (теория графов) — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия

Цикл (теория графов) — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия

Клика — (группа людей) шайка, банда, компания или сообщество людей. Клика (теория графов) полный подграф неориентированного графа. Клика (объединение художников) группа английских художников викторианской эпохи, основанная Ричардом Даддом … Википедия

Глоссарий теории графов — Эта страница глоссарий. См. также основную статью: Теория графов Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице) … Википедия

Словарь терминов теории графов — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И К Л М Н О П Р С … Википедия

Социальный граф — На данной анимации показаны в каких отношениях состоят разные социальные объекты. Пользователь Ева находится в дружеских отношениях с пользователями Адам и Кейт, при этом Адам и Кейт не являются друзьями друг другу, но у них есть общий друг Ева.… … Википедия

Задача о клике — относится к классу NP полных задач в области теории графов. Впервые она была сформулирована в 1972 году Ричардом Карпом.[1] … Википедия

Вершина (граф) — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия

Длина пути в орграфе — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия

Инцидентность — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия

Источник

На этот раз я представлю проект, реализацию на языке C# и методы тестирования для структуры данных графа, которые можно использовать для решения задачи о максимальной клике (maximum clique problem), или полном подграфе. Код графа также применим для многих других задач, как я поясню далее в этой статье.

Так что же такое задача о максимальной клике и почему она может пригодиться вам? Клика — это подмножество графа, где каждый узел соединен с каждым другим узлом. Взгляните на представление графа на рис. 1. Узлы 2, 4 и 5 образуют клику размером в три узла. Задача о максимальной клике заключается в нахождении клики с наибольшим размером в графе. Максимальная клика для графа на рис. 1 — это набор узлов < 0, 1, 3, 4 >, размер которого равен четырем.

Рис. 1. Граф для задачи о максимальной клике

Задача о максимальной клике встречается довольно часто, в том числе при анализе коммуникаций в социальных сетях, анализе компьютерных сетей, машинном распознавании образов и многих других. Даже в графах умеренного размера задача о максимальной клике оказывается одной из наиболее трудных и интересных в компьютерной науке. Методы, применяемые для решения задачи о максимальной клике, включают алгоритмы запрещенного поиска (tabu search), жадного поиска (greedy search), поиска плато (plateau search), параметрической адаптации в реальном времени (real-time parameter adaptation) и хронологии динамических решений (dynamic solution history). Эти методы можно использовать во многих других задачах. Короче говоря, код, решающий задачу о максимальной клике, может оказаться полезным непосредственно вам, а продвинутые методы, применяемые в алгоритме, — полезным для решения других сложных задач программирования.

Полное решение задачи о максимальной клике слишком длинное, чтобы его можно было представить и объяснить в одной статье, поэтому решение мы будем рассматривать в нескольких статьях. Первый шаг в решении задачи о максимальной клике — спроектировать, реализовать и проверить структуру данных, которая может эффективно хранить анализируемый граф в памяти. Консольное приложение на рис. 2 иллюстрирует, куда я клоню в этой статье.

Рис. 2. Загрузка и проверка графа

Если убрать ряд выражений WriteLine, код, выдающий то, что показано на рис. 2, выглядит так:

Данные для графа на рис. 1 хранятся во внешнем текстовом файле DimacsClique.clq, который использует стандартный формат DIMACS. Я кратко поясню этот формат файлов позже. Моя демонстрационная программа начинает с проверки исходного файла, затем создает экземпляр структуры данных графа, используя файл данных. После создания экземпляра графа я проверяю внутреннее представление и отображаю его в удобном для восприятия виде. Как вы увидите, эффективное внутреннее представление графа критически важно для задачи о максимальной клике. Демонстрационная программа заканчивает вызовом метода, который определяет, являются ли два узла смежными (узлы 5 и 8 в данном случае), и вызовом метода, который возвращает количество соседей для узла 4 в моем примере.

Я построчно проведу вас по коду, который сгенерировал вывод на рис. 2. Полный исходный код демонстрационной программы вы найдете в пакете, сопутствующем этой статье. Код написан на C#, но вы сможете следовать за мной на любом современном высокоуровневом языке, если владеете навыками программирования на среднем уровне. Представленный здесь код графа закладывает основу для решения задачи о максимальной клике в последующих статьях и должен стать полезным пополнением в вашем инструментарии.

Битовая матрица

Существует несколько распространенных способов представления невзвешенного (unweighted) (ребрам графа не назначены какие-либо приоритеты), ненаправленного (ребра не направлены от одного узла к другому) графа в памяти. Для задачи максимальной клики представление графа с использованием битовой матрицы обеспечивает великолепную комбинацию экономии пространства и эффективности работы с графом. На рис. 3 показана битовая матрица, соответствующая графу в примере. Хотя мы имеем дело с ненаправленным графом, принято называть индексы по вертикали выходящими узлами (from-nodes), а индексы по горизонтали — входящими узлами (to-nodes). Значение 1 обозначает наличие ребра между соответствующими узлами, а значение 0 — его отсутствие. Заметьте, что матрица симметрична и что мы предполагаем, что узлы не являются смежными самим себе.

Рис. 3. Представление графа в виде битовой матрицы

Основное преимущество битовой матрицы над альтернативными структурами заключается в том, что она обеспечивает быстрые операции поиска смежных узлов, а такие операции часто преобладают при выполнении многих алгоритмов, относящихся к графам, в том числе к задаче о максимальной клике. При грубой реализации главный недостаток битовой матрицы — большое использование памяти. Например, если бы матрица 9×9 на рис. 3 была реализована как двухмерный массив четырехбайтовых целых или булевых значений, то матрица потребовала бы 9 * 9 * 4 = 324 байта. Но, поскольку каждое значение в битовой матрице может быть только 0 или 1, мы можем использовать биты значения целого типа для хранения до 32 значений на каждого такое целое. В этом примере, если мы представим, что младший бит находится справа, первую строку можно сохранить как одно 32-битное целое 00000000-00000000-00000000-10110000, которое в десятичном виде будет иметь значение 128 + 32 + 16 = 176. Поэтому, если бы каждая строка матрицы хранилась как одно целое значение, где биты этого целого используются для представления наличия или отсутствия ребра между узлами, то матрица 9×9 потребовала бы всего 36 байтов.

Рис. 4. Класс BitMatrix

Использование BitMatrix могло бы выглядеть так:

Первая строка кода создает объект BitMatrix размером 9×9, изначально заполненный нулями (false), для представления невзвешенного, ненаправленного графа с девятью узлами. Вторая строка кода устанавливает строку 5, столбец 8 в true (1), указывая на наличие ребра между узлами 5 и 8. Третья строка кода устанавливает строку 8, столбец 5 в true (1), чтобы представление ребра графа было согласованным. Четвертая строка кода извлекает значение в строке 2, столбце 6, указывающее, имеется ли ребро между узлами 2 и 6, которое будет равно false (0). Заметьте, что определение того, являются ли два узла смежными, — это просто операция быстрого поиска в массиве.

Класс графа

Располагая классом BitMatrix, нетрудно определить эффективный класс графа, подходящий для задачи о максимальной клике и многих других задач, связанных с графами. Структура этого класса приведена на рис. 5. Класс графа имеет зависимости от пространств имен System, System.IO и System.Collections. В программе-примере я поместил класс графа непосредственно в консольное приложение, но, возможно, вы предпочтете выделить этот код в библиотеку классов.

Рис. 5. Определение класса графа

Определение класса графа начинается с:

Я присвоил классу графа имя MyGraph. Есть некоторый соблазн попытаться определить универсальный класс графа, но вариаций графов так много, что гораздо лучше определять разные классы графов для разных типов задач. Определенный здесь класс графа нацелен на решение задачи о максимальной клике и схожих задач, поэтому я мог бы назвать класс как-то наподобие MaxCliqueGraph. В классе четыре поля данных. Первое — объект BitMatrix, описанный ранее. Поля numberNodes и numberEdges хранят количество узлов (девять в этом примере) и число ненаправленных ребер в графе (13 в данном случае).

Когда решаешь многие задачи, связанные с графами, нужно знать, сколько соседей имеет некий узел, т. е. сколько узлов соединено с данным узлом. В примере графа на рис. 1 узел 5 имеет трех соседей. Количество соседей, имеющихся у какого-либо узла, также называется степенью узла (degree of the node), или степенью вершины (в терминологии графов понятия узла и вершины идентичны). Да данного узла это значение можно было бы при необходимости вычислять «на лету», подсчитывая количество значений true (1) в строке данных узла. Гораздо более быстрый способ — однократный подсчет и сохранение количества соседей для каждого узла в конструкторе графа с последующим поиском в массиве, если возникнет такая необходимость. Поэтому в примере графа после создания его экземпляра в массиве numberNeighbors было бы девять ячеек со значениями [3,3,2,3,6,3,1,3,2], указывающими, что узел 0 имеет три соседа, узел 1 — три соседа, узел 2 — два соседа и т. д.

Конструктор класса графа выглядит так:

Конструктор принимает текстовый файл, где хранятся данные графа, и строку, указывающую конкретный формат этого файла данных. Здесь я сразу же передаю управление вспомогательному методу LoadDimacsFormatGraph. Такая схема позволяет легко расширять класс графа для подстройки под множество форматов файлов данных. Если вы любитель перечислимых типов, параметр формата файла можно реализовать, используя перечисление.

В сердцевине класса MyGraph лежит метод LoadDimacsFormatGraph, который считывает файл исходных данных и сохраняет представление графа. Существует довольно много более-менее стандартных форматов файла графа. Я использую здесь формат DIMACS. Аббревиатура DIMACS расшифровывается так: Discrete Mathematics and Theoretical Computer Science. DIMACS является результатом коллективной разработки во главе с Университетом имени Ратгерса (Rutgers University).

Программа-пример, приведенная на рис. 2, использует файл DimacsGraph.clq, который перечислен на рис. 6. Строки, начинающиеся с буквы «c», являются комментариями. Одна строка начинается с буквы «p», за которой указана строка «edge» с количеством узлов и числом ребер. Строки, начинающиеся с буквы «e», определяют ребра. Заметьте, что файл формата DIMACS использует в качестве разделителей пробельные символы и числа с отсчетом от 1; кроме того, каждое ребро сохраняется только раз.

Рис. 6. Файл данных в формате DIMACS

Метод загрузки начинается с:

Я выполняю предварительное чтение, а затем продвигаюсь к строке «p» в файле данных. Поскольку со временем в текстовые файлы могут легко попасть случайные пробельные символы, я использую метод Trim, помогающий избавиться от таких проблем. Продолжаем:

Строку «p» я разбираю с помощью метода String.Split. К этому моменту tokens[0] хранит строковый литерал «p», tokens[1] — «edge», tokens[2] — «9», а tokens[3] — «13». Вызовом метода int.Parse (я мог применить Convert.ToInt32) количества узлов и ребер преобразуются в int-значения, сохраняемые в локальных переменных numNodes и numEdges. Эти значения в данный момент можно было бы записать в поля this.numberNodes и this.numberEdges класса графа. Теперь, определив количества узлов и ребер, я закрываю файл данных и создаю поле данных BitMatrix.

С этого момента я готов считывать остальные данные из файла:

Я снова открываю файл и читаю его от начала. Технически — из-за наличия строки «p» до любой строки «e» — нет никакой нужды дважды читать файл формата DIMACS. Однако для других форматов файлов, которые не хранят в явном виде количество ребер, вам может понадобиться двойной проход по аналогии с примененным здесь. Когда код встречает строку «e», такую как «e 3 6», я разбираю эту строку «e», преобразую два узла в тип int и вычитаю 1, чтобы изменить представление с отсчета от 1 на отсчет от 0. Я использую метод SetValue для создания симметричных записей в BitMatrix. Заметьте: поскольку BitMatrix симметричен, я мог бы сохранять лишь верхнюю или нижнюю часть треугольника (triangular portion) для уменьшения занимаемой памяти.

Потом я обрабатываю массив numberNeighbors:

Для каждого узла я прохожу соответствующую ему строку и подсчитываю количество значений true (1), которые дают число ребер, а значит, и количество соседей данного узла. Метод LoadDimacsFormatGraph заканчивается так:

После переноса количеств узлов и ребер из локальных переменных в поля класса я использую явный возврат, чтобы было понятнее, как происходит выход из этого метода.

Остальная часть класса MyGraph проста. Я предоставляю доступ к закрытым полям numberNodes и numberEdges класса как к значениям только для чтения, используя механизм C#-класса Property:

Работая с графами, трудно понять, когда следует выполнять стандартную проверку ошибок, а когда ее пропускать. Здесь я не проверяю, укладывается ли значение параметра node в диапазон от 0 до this.numberNodes–1, что оставляет меня уязвимым перед исключением в ситуации выхода индекса за границы диапазона. Обычно я добавляю проверки на ошибки в процессе разработки, а по ее окончании удаляю те проверки, которые можно безопасно убрать для большей производительности. Благодаря структуре данных, используемой классом BitMatrix, написать метод, который определяет, являются ли два узла смежными, весьма легко:

Вспомните, что BitMatrix симметричен, поэтому я могу проверять либо GetValue(nodeA, nodeB), либо GetValue(nodeB, nodeA). Как уже упоминалось, во многих алгоритмах, относящихся к графам, доминирует проверка смежности узлов. При использовании битовой матрицы такая проверка выполняется быстро, так как она складывается из простого поиска по массиву и некоторых манипуляций над битами, обрабатываемых классом BitArray.

Для своего класса MyGraph я написал простой метод ToString:

В задаче о максимальной клике производительность не является крупной проблемой, поэтому для метода ToString я использую простую конкатенацию строк вместо более эффективного класса StringBuilder. Здесь i служит индексом в строках BitMatrix, а j — индексом в столбцах. Строка завершается с помощью Environment.NewLine вместо «\n», что позволяет сделать мой класс MyGraph более портируемым.

Проверка графа

Если вы вернетесь к рис. 2, то заметите, что я выполняю два важных типа проверки графа: файла данных графа до создания экземпляра объекта графа и внутреннего представления графа после создания его экземпляра. Полное обсуждение проверки графа потребовало бы написания отдельной статьи, поэтому здесь я дам лишь краткий обзор.

Я выполняю проверку файла данных с помощью статического метода ValidateGraphFile, как показано на рис. 5. Как и в случае конструктора MyGraph, ValidateGraphFile сразу же вызывает вспомогательный метод ValidateDimacsGraphFile, который и делает реальную работу. Код проверки перебирает содержимое файла в цикле, чтобы увидеть, все ли строки имеют допустимую в DIMACS форму:

Этот метод также проверяет формат строк, отличных от комментариев, предпринимая попытку их разбора. Например, для одной строки «p»:

Для проверки строк «e» используется аналогичная логика. Этот шаблон, в целом, сохраняется при проверке любых файлов данных графа: проверка допустимости строк и попытка разбора строк данных.

После создания экземпляра я проверяю внутреннее представление графа с помощью метода ValidateGraph. Оказывается, полная проверка структуры данных графа на удивление сложна, поэтому на практике часто ограничиваются проверкой только на наиболее вероятные ошибки. Распространенная ошибка в файлах данных графов — отсутствующая строка данных, которая создает асимметричное хранилище данных BitMatrix. Это можно проверить таким кодом:

Другие ошибки, на которые стоит выполнять проверки, включают наличие true (1) в главной диагонали битовой матрицы, битовые матрицы, состоящие сплошь из false (0) или true (1), и неравенство суммы значений в поле-массиве numberNeighbors общему количеству значений true (1) в битовой матрице.

Больше деталей в следующих статьях

Джеймс Маккафри (Dr. James McCaffrey) работает на Microsoft Research в Редмонде (штат Вашингтон). Принимал участие в создании нескольких продуктов Microsoft, в том числе Internet Explorer и Bing. С ним можно связаться по адресу mjammc@microsoft.com.

Выражаю благодарность за рецензирование статьи экспертам Полу Коху (Paul Koch), Дэну Либлингу (Dan Liebling), Энн Лумис Томпсон (Ann Loomis Thompson) и Шейну Уильямсу (Shane Williams).

Источник

Клика (теория графов)

Хотя изучение полных подграфов началось ещё с формулировки теоремы Рамсея в терминах теории графов Эрдёшем и Секерешем. Термин «клика» пришёл из работы Люка и Пери, использовавших полные подграфы при изучении социальных сетей для моделировании клик людей, то есть групп людей, знакомых друг с другом. Клики имеют много других приложений в науке, и, в частности, в биоинформатике.

Связанные понятия

Упоминания в литературе

Связанные понятия (продолжение)

В теории графов совершенным графом называется граф, в котором хроматическое число любого порождённого подграфа равно размеру максимальной клики этого подграфа. Благодаря строгой теореме о совершенных графах, с 2002 года известно, что совершенные графы — это то же самое, что и графы Бержа. Граф G является графом Бержа если ни G, ни его дополнение не имеет порождённых циклов нечётной длины (5 и более рёбер).

В теории графов графом без клешней называется граф, который не содержит порождённых подграфов, изоморфных K1,3 (клешней).

В теории графов неориентированный граф H называется минором графа G, если H может быть образован из G удалением рёбер и вершин и стягиванием рёбер.

В теории графов вершиной называется фундаментальная единица, образующая графы — неориентированный граф состоит из множества вершин и множества рёбер (неупорядоченных пар вершин), в то время как ориентированный граф состоит из множества вершин и множества дуг (упорядоченных пар вершин). На рисунках, представляющих граф, вершина обычно обозначается кружком с меткой, ребро — линией, дуга — стрелкой, соединяющей вершины.

В теории графов графом-циклом называется граф, состоящий из единственного цикла, или, другими словами, некоторого числа вершин, соединённых замкнутой цепью. Граф-цикл с n вершинами обозначают как Cn. Число вершин в Cn равно числу рёбер и каждая вершина имеет степень 2, то есть любая вершина инцидентна ровно двум рёбрам.

В теории графов графом гиперкуба Qn называется регулярный граф с 2n вершинами, 2n−1n рёбрами и n рёбрами, сходящимися в одной вершине. Его можно получить как одномерный скелет геометрического гиперкуба. Например, Q3 — это граф, образованный 8 вершинами и 12 рёбрами трёхмерного куба. Граф можно получить другим образом, отталкиваясь от семейства подмножеств множества с n элементами путём использования в качестве вершин все подмножества и соединением двух вершин ребром, если соответствующие множества.

В теории графов рёберным графом L(G) неориентированного графа G называется граф L(G), представляющий соседство рёбер графа G.

Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице).

В теории графов outerplanar graph — это граф, допускающий планарную диаграмму, в которой все вершины принадлежат внешней грани.

В теории графов графом Халина называется некоторый вид планарного графа, который строится из дерева, имеющего по меньшей мере 4 вершины, ни одна из которых не имеет в точности двух соседей. Дерево рисуется на плоскости так, что никакие рёбра не пересекаются, затем добавляются рёбра, соединяющие все его листья в цикл. Графы Халина названы по имени немецкого математика Рудольфа Халина, изучавшего их в 1971 году, но кубические графы Халина изучались за столетие до этого английским математиком Томасом.

В теории графов короной с 2n вершинами называется неориентированный граф с двумя наборами вершин ui и vi и рёбрами между ui и vj, если i ≠ j. Можно рассматривать корону как полный двудольный граф, из которого удалено совершенное паросочетание, как двойное покрытие двудольным графом полного графа, или как двудольный граф Кнезера Hn,1, представляющий подмножества из 1 элемента и (n − 1) элементов множества из n элементов с рёбрами между двумя подмножествами, если одно подмножество содержится в другом.

В теории графов графом пересечений называется граф, представляющий схему пересечений семейства множеств. Любой граф можно представить как граф пересечений, но некоторые важные специальные классы можно определить посредством типов множеств, используемых для представления в виде пересечений множеств.

Источник

Задача о клике

Задача о клике относится к классу NP-полных задач в области теории графов. Впервые она была сформулирована в 1972 году Ричардом Карпом. [1]

Кликой в неориентированном графе называется подмножество вершин, каждые две из которых соединены ребром графа. Иными словами, это полный подграф первоначального графа. Размер клики определяется как число вершин в ней. Задача о клике существует в двух вариантах: в задаче распознавания (англ.) требуется определить, существует ли в заданном графе G клика размера k, в то время как в вычислительном варианте требуется найти в заданном графе G клику максимального размера.

Содержание

NP-полнота

NP-полнота задачи о клике следует из NP-полноты задачи о независимом множестве (вершин). Легко показать, что необходимым и достаточным условием для существования клики размера k является наличие независимого множества размера не менее k в дополнении графа. Это очевидно, поскольку полнота подграфа означает, что его дополнение не содержит ни одного ребра.

Другое доказательство NP-полноты можно найти в книге «Алгоритмы: построение и анализ». [2]

Алгоритмы

Как и для других NP-полных задач, эффективного алгоритма для поиска клики заданного размера на данный момент не найдено. Полный перебор всех возможных подграфов размера k с проверкой того, является ли хотя бы один из них полным, — неэффективен, поскольку полное число таких подграфов в графе с v вершинами равно биномиальному коэффициенту

Другой алгоритм работает так: две клики размера n и m «склеиваются» в большую клику размера n+m, причём кликой размера 1 полагается отдельная вершина графа. Алгоритм завершается, как только ни одного слияния больше произвести нельзя. Время работы данного алгоритма линейно, однако он является эвристическим, поскольку не всегда приводит к нахождению клики максимального размера. В качестве примера неудачного завершения можно привести случай, когда вершины, принадлежащие максимальной клике, оказываются разделены и находятся в кликах меньшего размера, причём последние уже не могут быть «склеены» между собой.

См. также

Примечания

Литература

Ссылки

Полезное

Смотреть что такое «Задача о клике» в других словарях:

Задача о независимом множестве — относится к классу NP полных задач в области теории графов. Эквивалентна задаче о клике. Содержание 1 Определения 2 Максимальное независимое множество в дереве … Википедия

Задача о независимом наборе — Задача о независимом множестве относится к классу NP полных задач в области теории графов. По сути, она полностью эквивалентна задаче о клике. Независимый набор из 9 голубых вершин Множество вершин графа называется независимым, если никакие две… … Википедия

Задача о покрытии множества — является классическим вопросом информатики и теории сложности. Данная задача обобщает NP полную задачу о вершинном покрытии (и потому является NP сложной). Несмотря на то, что задача о вершинном покрытии сходна с данной, подход, использованный в… … Википедия

Задача SAT — Задача выполнимости булевых формул (SAT или ВЫП) задача распознавания, важная для теории вычислительной сложности. Экземпляром задачи SAT является булева формула, состоящая только из имен переменных, скобок и операций (И), (ИЛИ) и (HE). Задача… … Википедия

Задача ВЫП — Задача выполнимости булевых формул (SAT или ВЫП) задача распознавания, важная для теории вычислительной сложности. Экземпляром задачи SAT является булева формула, состоящая только из имен переменных, скобок и операций (И), (ИЛИ) и (HE). Задача… … Википедия

Задача о вершинном покрытии — NP полная задача информатики в области теории графов. Часто используется в теории сложности для доказательства NP полноты более сложных задач. Содержание 1 Определение 2 NP полнота 3 Ссылки … Википедия

Задача о коммивояжере — Задача коммивояжёра (коммивояжёр бродячий торговец) является одной из самых известных задач комбинаторной оптимизации. Задача заключается в отыскании самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу с… … Википедия

Задача о коммивояжёре — Задача коммивояжёра (коммивояжёр бродячий торговец) является одной из самых известных задач комбинаторной оптимизации. Задача заключается в отыскании самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу с… … Википедия

Задача коммивояжера — Задача коммивояжёра (коммивояжёр бродячий торговец) является одной из самых известных задач комбинаторной оптимизации. Задача заключается в отыскании самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу с… … Википедия

Задача о рюкзаке — Задача о ранце (рюкзаке) одна из задач комбинаторной оптимизации. Название это получила от максимизационной задачи укладки как можно большего числа нужных вещей в рюкзак при условии, что общий объём (или вес) всех предметов ограничен. Подобные… … Википедия

Источник