что такое кинетическая энергия материальной точки
Формула кинетической энергии
Определение и формула кинетической энергии
Кинетическую энергию тела определяют при помощи работы, которая совершается телом при его торможении от начальной скорости, до скорости, равной нулю.
Кинетическая энергия тела – мера механического движения тела. Она зависит от относительной скорости тел.
Встречаются следующие обозначения кинетической энергии: Ek,Wk,T.
Работу, которую производят над телом (A’) можно связать с изменением его кинетической энергии:
Кинетическая энергия материальной точки и тела
Кинетическая энергия материальной точки равна:
где m – масса материальной точки, p – импульс материальной точки, v – скорость ее движения. Кинетическая энергия является скалярной физической величиной.
Если тело нельзя принять за материальную точку, то его кинетическая энергия рассчитывается как сумма кинетических энергий всех материальных точек, которые составляют исследуемое тело:
В том случае, если тело (отличное от материальной точки) движется поступательно, то его кинетическую энергию можно рассчитать, применяя формулу (2), в которой все параметры отнесены к телу в целом.
При вращении тело вокруг неподвижной оси его кинетическую энергию можно вычислить, применяя формулу:
Если твердое тело совершает вращение относительно неподвижной точки (например, точки O), то его кинетическую энергию находят как:
Единицы измерения кинетической энергии
Основной единицей измерения кинетической энергии (как и любого другого вида энергии) в системе СИ служит:
в системе СГС –[Ek]= эрг.
При этом: 1 дж= 10 7 эрг.
Теорема Кенига
Для самого общего случая при расчете кинетической энергии применяют теорему Кенига. В соответствии с которой, кинетическая энергия совокупности материальных точек есть сумма кинетической энергии поступательного перемещения системы со скоростью центра масс (vc) и кинетической энергии (E’k) системы при ее относительном движении к поступательному перемещению системы отсчета. При этом начало системы отсчета связывают с центром масс системы. Математически данную теорему можно записать как:
Так, если рассматривать твердое тело, то его кинетическую энергию можно представить как:
Примеры решения задач
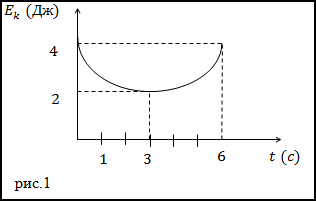
Задание. Какова работа, которая производится над телом за t=3 c (с начала отсчета времени), при силовом взаимодействии, если изменение кинетической энергии исследуемого тела задано графиком (рис.1)?
Решение. По определению изменение кинетической энергии равно работе (A’), которая производится над телом при силовом взаимодействии, то есть можно записать, что:
Исследуя график, приведенный на рис.1 мы видим, что за время t=3 c кинетическая энергия тела изменяется от 4 Дж до 2 Дж, следовательно:
Ответ. A’=-2 Дж.
Формула кинетической энергии не по зубам? Тебе ответит эксперт через 10 минут!
Решение. В качестве основы для решения задачи используем формулу, определяющую кинетическую энергию материальной точки:
Но по условию задачи:
Следовательно, можно приравнять правые части выражений (2.1) и (2.2), и получить:
Из второго закона Ньютона нам известно, что сила, действующая на частицу, будет равна:
При этом нормальное ускорение частицы (an), перемещающейся по окружности найдем как:
Тангенциальную составляющую ускорения (aт)используя определение тангенциального ускорения, определение скорости ($v=\frac
Используем выражения: (2.5), (2.6), (2.7), окончательно получаем для модуля силы:
Физика. 10 класс
Конспект урока
Урок 13. Работа. Мощность. Энергия. Закон сохранения механической энергии
Перечень вопросов, рассматриваемых на уроке:
3. Механическая энергия
4. Закон сохранения механической энергии.
Работа постоянной силы равна произведению модулей силы и перемещения точки приложения силы и косинуса угла между ними.
Мощность – отношение работы к интервалу времени, за который эта работа совершена.
Кинетическая энергия– энергия, которой обладает движущееся тело.
Кинетическая энергия материальной точки – величина равная половине произведения массы материальной точки на квадрат её скорости.
Теорема об изменении кинетической энергии: изменение кинетической энергии материальной точки при её перемещении равно работе, совершённой силой, действующей на точку при этом перемещении.
Если на точку действуют несколько сил, то изменение её кинетической энергии равно алгебраической сумме работ всех сил, действующих на неё.
Работа силы тяжести зависит только от положений начальной и конечной точек траектории и не зависит от формы траектории. При движении тела по замкнутой траектории работа силы тяжести равна нулю.
Консервативными силами называют силы, работа которых не зависит от формы траектории точки приложения силы и по замкнутой траектории равна нулю.
Работа силы упругости при растяжении пружины, т.е. когда направление силы противоположно перемещению тела, меньше нуля. Если начальное и конечное состояния пружины совпадают, то суммарная работа силы упругости при деформации пружины равна нулю.
Потенциальной энергией тела в поле силы тяжести называют величину, равную произведению массы тела на ускорение свободного падения и на высоту тела над поверхностью Земли.
Потенциальной энергией упругодеформированного тела называют величину, равную половине произведения коэффициента упругости тела на квадрат удлинения или сжатия.
Потенциальная энергия – энергия взаимодействия тел, обусловленная их взаимным расположением или взаимным расположением частей тела.
Полная механическая энергия равна сумме кинетической и потенциальной энергий тел, входящих в систему.
Закон сохранения энергии – энергия не создаётся и не уничтожается, а только превращается из одной формы в другую.
Основная и дополнительная литература по теме урока
Мякишев Г.Я., Буховцев Б.Б, Сотский Н.Н. Физика. 10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. С. 131-147.
Рымкевич А.П. Сборник задач по физике. 10-11 класс.-М.:Дрофа,2009. С.49-56.
ЕГЭ 2017. Физика. 1000 задач с ответами и решениями. Демидова М.Ю., Грибов В.А., Гиголо А.И. М.: Экзамен, 2017.
Теоретический материал для самостоятельного изучения
Влияние на тело сил, приводящее к изменению модуля их скорости, характеризуется величиной, которая зависит как от сил, так и от перемещения тел. Эта величина в механике называется работой силы, определяется по формуле:
Эта формула справедлива в случае, когда проекция силы на смещение постоянна.
Если есть угол между силой и смещением, то проекция силы равна произведению силы на косинус этого угла.
В этом случае работа постоянной силы равна произведению модулей силы и смещения точки приложения силы и косинуса угла между ними.
Если сила F перпендикулярна перемещению тела, то работа, этой силой равна нулю. Это тот случай, когда действует сила, но тело не двигается.
Если на тело действует несколько сил, проекция результирующей силы на перемещение равна сумме проекций отдельных сил.
Поэтому суммарная работа, (алгебраическая сумма работ всех сил), равна работе результирующей силы.
В жизни важно те только совершение работы, но и время, за которое выполняется работа. Работу мы можем делать быстро и медленно. Отношение работы к временному интервалу, за который выполняется эта работа называется мощностью.
Как вы думаете, что необходимо для движения тела? Да, энергия необходима. Энергия характеризует способность тела (или системы тел) совершать работу. Кинетическая энергия – энергия, которой обладает движущееся тело
И энергия может быть кинетической и потенциальной.
Кинетическая энергия материальной точки равна половине массы материальной точки на квадрат её скорости:
Теорема об изменении кинетической энергии: изменение кинетической энергии материальной точки при её перемещении равно работе силы, действующей на точку во время этого перемещении.
Работа силы тяжести не зависит от формы траектории, а зависит только от положений начальной и конечной точек траектории
При движении тела по замкнутой траектории работа силы тяжести равна нулю.
Силы, работа которых не зависит от формы траектории точки приложения силы и на замкнутой траектории равна нулю, называют консервативными силами.
Работа при растяжении пружины силы упругости, когда направление силы совпадает с направлением движения тела, принимает положительные значения и определяется по формуле:
В случае при увеличении деформации пружины, когда сила упругости, действующая на тело со стороны пружины, направлена противоположно деформации, работа силы упругости отрицательна:
Согласно теореме, об изменении кинетической энергии ΔЕк = Ек2 – Ек1 работа силы, действующей на тело, равна изменению его кинетической энергии:
Если силы взаимодействия между телами консервативны, то работу сил можно представить, как разность двух значений некоторой величины, зависящей от взаимного расположения тел или частей одного тела: А = mgh1 – mgh2, работы силы тяжести
и работы силы упругости.
Величина, равная произведению массы m тела на ускорение свободного падения g и высоту h тела над поверхностью Земли, называется потенциальной энергией тела в поле силы тяжести.
Закон сохранения механической энергии:
В изолированной системе, в которой действуют консервативные силы, механическая энергия сохраняется.
Закон сохранения механической энергии является частным случаем общего закона сохранения энергии: энергия не создаётся и не разрушается, а преобразуется из одной формы в другую.
Примеры и разбор решения заданий
Тело движется вдоль оси ОХ под действием силы F = 2 Н, направленной вдоль этой оси. На рисунке приведён график зависимости проекции скорости vх тела на эту ось от времени t. Какую мощность развивает эта сила в момент времени t = 3 с?
Решение: по графику проекция скорости в момент времени 3с, равна 5 м/с. Мощность, развиваемая силой F для тела, движущегося со скоростью можно найти по формуле
m = 15т = 15 ·10 3 кг
Запишем уравнение второго закона Ньютона:
в проекции на ось ОХ:
Fтр = µmg → Fт = ma + µmg = m(a+ µg);
По определению работы:
Aт = 15 ·10 3 кг (1,4 м/с 2 +0,05 ·10 м/с 2 ) ·10 м = 285 кДж
Кинетическая энергия определяется по формуле:
Ек = mv 2 /2. Скорость определим по формуле:
Ек = 15·10 3 кг·14 м/с 2 = 210 кДж
Физика Б1.Б8.
Электронное учебное пособие по разделу курса физики Механика
Механика – это раздел физики, который изучает наиболее простой вид движения материи – механическое движение и причины, вызывающие или изменяющие это движение.
Механика состоит из трех разделов: кинематики, динамики и статики. Кинематика дает математическое описание движения, не касаясь причин, которыми вызвано движение. Динамика – основной раздел механики, она изучает законы движения тел и причины, которыми вывзывается движение и его изменение. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных разделов – кинематики и динамики.
Введение
Механика – это раздел физики, который изучает наиболее простой вид движения материи – механическое движение и причины, вызывающие или изменяющие это движение.
Механическое движение – это изменение во времени взаимного расположения тел или частей одного и того же тела. Причиной, вызывающей механическое движение тела или его изменение, является воздействие со стороны других тел.
Развитие механики началось еще в древние времена, однако, как наука она формировалась в средние века. Основные законы механики установлены итальянским физиком и астрономом Г. Галилеем (1564-1642) и английским ученым И. Ньютоном (1643-1727).
Механику Галилея-Ньютона принято называть классической механикой. В ней изучается движение макроскопических тел, скорости которых значительно меньше скорости света с в вакууме. Законы движения тел со скоростями, близкими к скорости света сформулированы А. Эйнштейном (1879-1955), они отличаются от законов классической механики. Теория Эйнштейна называется специальной теорией относительности и лежит в основе релятивистской механики. Законы классической механики неприемлемы к описанию движения микроскопических тел (элементарных частиц – электронов, протонов, нейтронов, атомных ядер, самих атомов и т.д.) их движение описывается законами квантовой механики.
Механика состоит из трех разделов: кинематики, динамики и статики. Кинематика дает математическое описание движения, не касаясь причин, которыми вызвано движение. Динамика – основной раздел механики, она изучает законы движения тел и причины, которыми вывзывается движение и его изменение. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных разделов – кинематики и динамики.
В механике для описания движения в зависимости от условий решаемой задачи пользуются различными упрощающими моделями: материальная точка, абсолютно твердое тело, абсолютно упругое тело, абсолютно неупругое тело, и т.д. Выбор той или иной модели диктуется необходимостью учесть в задаче все существенные особенности реального движения и отброс ить несущественные, усложняющие решение.
Материальная точка – это тело обладающее массой, размеры и форма которого несущественны в данной задаче. Любое твердое тело или систему тел можно рассматривать как систему материальных точек. Для этого любое тело или тела системы нужно мысленно разбить на большое число частей так, чтобы размеры каждой части были пренебрежимо малы по сравнению с размерами самих тел.
Абсолютно твердое тело – это тело, расстояние между любыми точками которого остается неизменным в процессе движения или взаимодействия. Эта модель пригодна, когда можно пренебречь деформацией тел в процессе движения.
Абсолютно упругое и абсолютно неупругое тело – это два предельных случая реальных тел, деформациями которых можно и нельзя пренебречь в изучаемых процессах.
Любое движение рассматривается в пространстве и времени. В пространстве определяется местоположение тела, во времени происходит смена местоположений или состояний тела в пространстве, время выражает длительность состояния движения или процесса. Пространство и время –это два фундаментальных понятия, без которых теряется смысл понятия движения: движения не может быть вне времени и пространства.
Кинетическая и потенциальная энергии
Кинетическая энергия
Работа всех сил, действующих на тело, равна работе равнодействующей силы.
Как видим, работа, совершенная силой, пропорционально изменению квадрата скорости тела.
Определение. Кинетическая энергия
Кинетическая энергия тела равна половине произведения массы тела на квадрат его скорости.
Теорема о кинетической энергии
Вновь обратимся к рассмотренному примеру и сформулируем теорему о кинетической энергии тела.
Теорема о кинетической энергии
Работа приложенной к телу силы равна изменению кинетической энергии тела. Данное утверждение справедливо и тогда, когда тело движется под действием изменяющейся по модулю и направлению силы.
Чтобы остановить тело, нужно совершить работу
Потенциальная энергия
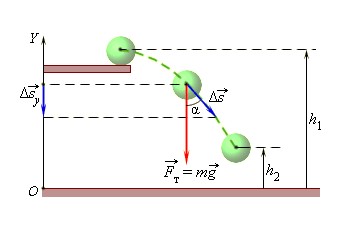
Например, тело поднято над поверхностью земли. Чем выше оно поднято, тем больше будет потенциальная энергия. Когда тело падает вниз под действием силы тяжести, эта сила совершает работу. Причем работа силы тяжести определяется только вертикальным перемещением тела и не зависит от траектории.
Вообще о потенциальной энергии можно говорить только в контексте тех сил, работа которых не зависит от формы траектории тела. Такие силы называются консервативными.
Примеры консервативных сил: сила тяжести, сила упругости.
Когда тело движется вертикально вверх, сила тяжести совершает отрицательную работу.
При этом сила тяжести совершила работу, равную
Определение. Потенциальная энергия
Можно говорить о потенциальной энергии в поле силы тяжести, потенциальной энергии сжатой пружины и т.д.
Работа силы тяжести равна изменению потенциальной энергии, взятому с противоположным знаком.
Ясно, что потенциальная энергия зависит от выбора нулевого уровня (начала координат оси OY). Подчеркнем, что физический смысл имеет изменение потенциальной энергии при перемещении тел друг относительно друга. При любом выборе нулевого уровня изменение потенциальной энергии будет одинаковым.
При расчете движения тел в поле гравитации Земли, но на значительных расстояниях от нее, во внимание нужно принимать закон всемирного тяготения (зависимость силы тяготения от расстояния до цента Земли). Приведем формулу, выражающую зависимость потенциальной энергии тела.
Потенциальная энергия пружины
При этом работа силы упругости при изменении длины пружины на x в обоих случаях была одинакова и равна
Величина E у п р = k x 2 2 называется потенциальной энергией сжатой пружины. Она равна работе силы упругости при переходе из данного состояния тела в состояние с нулевой деформацией.
Кинетическая энергия материальной точки









Кинетическая энергия
Кинетическая энергия как точки, так и системы не зависит от направления скорости точки. Только когда все точки системы неподвижны, кинетическая энергия системы равна нулю. Расчет кинетической энергии системы (теорема Кенига). Движение механической системы разлагается на поступательный перевод с центром тяжести системы, а система координат, которая переводится с центром тяжести, используется в качестве эталона. Для каждой точки в системе Mk (см. Рис. 57), а также того, как это было сделано при выводе формулы момента движения с таким расширением абсолютного движения, P * = Pc + ‘!
Известно, что по инерции без действия сил материальные точки могут двигаться с постоянной скоростью по прямой, а твердые тела-вращаться вокруг неподвижной оси с постоянной угловой скоростью. Людмила Фирмаль
В соответствии с этим Где v ^ —dr / dt — относительная скорость точки. Это происходит потому, что движущаяся система координат движется постепенно (ω = 0), поэтому полная производная по времени от rk соответствует локальной производной, равной относительной скорости точки. Подставляя значение скорости vk в кинетическую энергию абсолютного движения системы, то есть кинетическую энергию относительного движения относительно системы координат Ox1u121, получается очевидное преобразование. но с того времени = const = 0.
Учитывая, что mk = M — масса системы, второе слагаемое в (62) (63) где Сумма Г? 1 — кинетическая энергия относительного движения системы относительно системы координат, которая постепенно движется вместе с центром тяжести, или кинетическая энергия системы относительно центра тяжести. Уравнение (63) представляет собой так называемую теорему Кенига: кинетическая энергия системы абсолютного движения — это кинетическая энергия центра масс, когда вся масса системы сконцентрирована в нем, и Общая кинетическая энергия. Твердая кинетическая энергия. Поступательное движение твердой кинетической энергии (S), Во время перемещения твердого тела v — общая скорость всех точек тела, поскольку скорость всех точек тела одинакова, то есть vk = v.
Таким образом, кинетическая энергия перемещаемого твердого тела рассчитывается так же, как и одна точка, масса которой равна массе всего тела. Когда тело вращается вокруг фиксированной оси, кинетическая энергия может быть рассчитана с учетом того, что скорость точки на теле Mk может быть выражена следующим образом (см. Рисунок 50). vk = cahk. Где hk — кратчайшее расстояние от точки Mk до оси вращения. И — угловая скорость тела. тогда м == у ^ = ^ у ж 2 2 ’* 2 или (65) где Jz — момент инерции тела относительно оси вращения Oz. Таким образом, кинетическая энергия объекта при вращательном движении вокруг неподвижной оси равна половине произведения момента инерции объекта относительно оси вращения, обусловленного квадратом угловой скорости объекта.
Из сравнения (64) и (65) видно, что эгида формулы аналогична. Только для вращательного движения, аналог массы — это момент инерции тела относительно оси вращения, а скорость — угловая скорость тела. Это сходство между поступательным и вращательным движением твердого тела можно наблюдать во многих формулах, связанных с этими двумя движениями. Для твердого плоского движения кинетическая энергия может быть рассчитана по теореме Кенига. В этом случае относительное движение к центру тяжести (точнее, относительное движение к движущейся системе координат (С поступательным центром тяжести) вращается вокруг центра тяжести с угловой скоростью ω.
Где JCz — момент инерции объекта вокруг оси Cz, который проходит через центр масс объекта, перпендикулярный плоскости движения. Поэтому, исходя из (63), о плоском движении тела + (66) Таким образом, в плоском движении тела кинетическая энергия представляет собой сумму кинетической энергии и центра масс поступательного движения тела и кинетической энергии от вращения вокруг оси, проходящей через центр масс и перпендикулярной плоскости движения. Учитывая vc = wCP (P — центр мгновенной скорости), мы используем теорему Штейнера из (66), чтобы получить другое уравнение для кинетической энергии твердого тела в плоском движении. r = m2 + L-.4- «’ p di; = Fdf, Где v = dr / dt — скорость точки. di5 = d ^. с того времени mv • d6 = d (mv 2/2) = d (mv2 / 2) и, наконец, d (mv2l2) = дА. (67) Уравнение (67) выражает теорему об изменении кинетической энергии точки в дифференциальной форме.
В настоящей работе выведено правило сохранения момента движения системы и рассмотрена материальная точка как механическая система, в которой число точек равно единице. Людмила Фирмаль
Изменение кинетической энергии системы при перемещении из одного положения в другое равно сумме работы всех внешних и внутренних сил, действующих на систему при соответствующем смещении системной точки в том же положении. Особый случай. Для абсолютно твердых тел суммарная работа всех внутренних сил в системе равна нулю: Meaux Таким образом, теорема об изменении кинетической энергии может быть выражена, например, в окончательном виде: T-T0 = 2A [´ ‘. (71) Изменение кинетической энергии твердого тела при любом смещении равно сумме работы всех внешних сил, действующих на объект при соответствующем смещении точки объекта при одинаковом смещении твердого тела.
Таким образом, в отличие от других общих теорем системной динамики, внутренние силы могут ввести теорему об изменении кинетической энергии. Абсолютно твердые тела не включены в эту теорему. Пример I. В маятнике Максвелла однородный цилиндр радиуса R падает без начальной скорости и наматывается вокруг центра цилиндра. В зависимости от высоты спуска определяется скорость оси цилиндра (рис. 69). Решения. Согласно теореме об изменении кинетической энергии системы, состоящей из нагрузки, резьбы, блока и катка Здесь T0 = 0.
Потому что сначала была система. Укажите Г. Нагрузка T2 и T3 кинетическая энергия, блок за падением соответственно При загрузке до высоты L, так но — (2e + sp + P) = — (e + 2 />). Поскольку внутренняя работа натяжения нити равна нулю, вся сплошная система, соединенная нитью, обычно составляет £ 1 ° = 0. Поскольку эти силы приложены к неподвижной точке O, сила тяжести устройства и реакция osn P работают равными нулю.
Поскольку сила тяжести ролика P перпендикулярна смещению, а силы N, F и p приложены к мгновенному центру скорости, работа равна нулю. Работа выполняется парой сил с силой Q и моментом Mk, препятствующих вращению ролика вдоль плоскости. У нас есть £ L1 ‘’- (> L-L4
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института