что такое калибровка камеры видеонаблюдения
Калибровка камеры с использованием с OpenCV
Камера является неотъемлемой частью многих автоматизированных систем, например, в робототехнике, в наблюдениях и исследовании космоса, в социальных сетях, промышленной автоматизации и даже в индустрии развлечений.
Для эффективного использования камер во многих приложениях особенно важно знать их характеристики.
Здесь вы узнаете шаги калибровки камеры и поймете их значение. Кроме того, на примере шахматной доски мы поделимся кодом Python для калибровки.
Что такое калибровка камеры?
Калибровка એ — это процесс оценки параметров камеры.
Это значит, что у нас есть полная информация (технические характеристики или расчетные коэффициенты) о камере, необходимые для определения точной взаимосвязи между 3D‑точкой в реальном мире и соответствующим 2D‑изображением, проекцией (каждым пикселем) на изображении, снятом откалиброванной камерой.
Обычно для этого необходимо получить два вида параметров:
На рисунке ниже для искажения изображения были использованы параметры объектива, оцененные при геометрической калибровке.

Калибровка камеры с использованием OpenCV
Для понимания процесса калибровки, нам сначала необходимо понять геометрию формирования изображения. Как показано в предыдущей публикации (желательно её прочитать, нажав на ссылку), чтобы найти проекцию 3D‑точки на плоскость изображения, сначала надо перевести точку (X_w, Y_w, Z_w) из мировой системы координат в систему координат камеры с учётом внешних параметров (Вращение R и Смещение t ).
\mathbf
= \mathbf
Как упоминалось в предыдущем посте, внутренняя матрица \mathbf
где, f_x, f_y — фокусные расстояния x и y (да, они обычно одинаковы).
c_x, c_y — координаты x и y оптического центра в плоскости изображения. Использование центра изображения обычно является достаточно хорошим приближением.
\gamma — это перекос между осями. Обычно это 1.
Цель калибровки камеры
Таким образом, алгоритм калибровки камеры имеет следующие входы и выходы:
Примечание. В OpenCV встроенная матрица камеры не имеет параметра перекоса. Таким образом, матрица имеет вид
Методы калибровки камеры
Ниже перечислены основные методы калибровки камеры:
Калибровка камеры — шаг за шагом
Процесс калибровки объясняется блок-схемой, приведенной ниже.
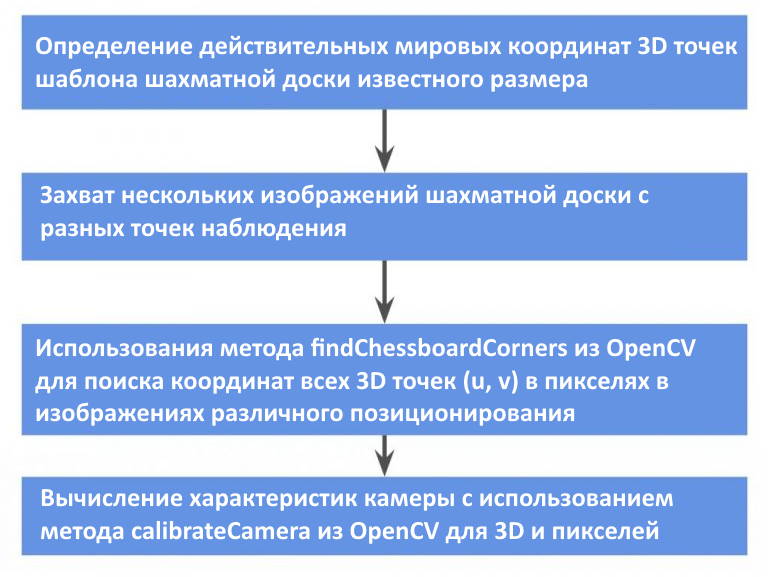
Шаг 1: Определение действительных мировых координат 3D точек шаблона шахматной доски известного размера
Наши 3D точки — это углы клеток шахматной доски. Любой угол доски может быть выбран в качестве начала мировой системы координат. Оси X_w и Y_w расположены вдоль стены, а ось Z_w перпендикулярна стене. Поэтому все точки на шахматной доске находятся на плоскости XY (т.е. Z_w = 0 ).
Почему шахматная доска так широко используется в калибровке?
Клетки шахматной доски легко различимы на изображении и их легко обнаружить. Более того, углы клеток шахматной доски идеально подходят для их локализации, поскольку имеют резкие градиенты в двух направлениях. Кроме того, углы находятся на пересечении линий шахматной доски. Все эти факторы определяют надежность поиска углов клеток, расположенных в шахматном порядке.

Шаг 2: Захват нескольких изображений шахматной доски с разных точек наблюдения
Затем, не изменяя местоположение нашей шахматной доски, мы делаем несколько снимков, смещая камеру.
Можно зафиксировать камеру, а смещать шахматную доску. С точки зрения математики это одно и то-же.
Шаг 3: Вычисление 2D координат клеток шахматной доски в пикселях
Теперь у нас есть несколько изображений шахматной доски. Мы знаем 3D координаты точек шахматной доске. Последнее, что нам нужно, это координаты углов клеток шахматной доски на изображениях в пикселях.
3.1 Поиск углов шахматной доски
Возвращаемое значение функции true или false в зависимости от того, был обнаружен шаблон или нет.
3.2 Уточнение координат клеток шахматной доски
Хорошая калибровка — это точность. Чтобы получить хорошие результаты, важно получить координаты клеток с субпиксельной точностью.
Функция OpenCV cornerSubPix берет клетки исходного изображения и ищет лучшее местоположение углов клеток, расположенных по соседству. По своей сути алгоритм является итерационным и поэтому нам необходимо указать критерии завершения (например, количество итераций и/или точность).
Python
Step 4: Калибровка камеры
Последний шаг калибровки состоит в том, чтобы передать 3D-точки в мировых координатах и их 2D-положения на всех изображениях в метод calibrateCamera OpenCV. Реализация основана на статье «A Flexible New Technique for Camera
Calibration» Чжэнъю Чжан. Математика немного сложна и требует знания линейной алгебры.
Давайте посмотрим на синтаксис calibrateCamera :
Код для калибровки камеры
Код для калибровки камеры приведен ниже. Однако загрузить все изображения и код намного проще, посетив Github.
Скрипт Python для калибровки камер
Пожалуйста, внимательно прочитайте комментарии, объясняющие каждыйшаг
Калибровка Kinect v2 с помощью OpenCV на Python
Не так давно мы начали пару проектов, в которых необходима оптическая система с каналом дальности, и решили для этого использовать Kinect v2. Поскольку проекты реализуются на Python, то для начала нужно было заставить работать Kinect из Python, а затем откалибровать его, так как Kinect из коробки вносит некоторые геометрические искажения в кадры и дает сантиметровые ошибки в определении глубины.
До этого я никогда не имел дела ни с компьютерным зрением, ни с OpenCV, ни с Kinect. Исчерпывающую инструкцию, как со всем этим хозяйством работать, мне найти тоже не удалось, так что в итоге пришлось порядком повозиться. И я решил, что будет не лишним систематизировать полученный опыт в этой статье. Быть может, она окажется небесполезной для какого-нибудь страждущего, а еще нам нужна популярная статья для галочки в отчетности.
Минимальные системные требования: Windows 8 и выше, Kinect SDK 2.0, USB 3.0.
Таблица I. Характеристики Kinect v2:
| Разрешение RGB камеры, пикс. | 1920 x 1080 |
| Разрешение инфракрасной (ИК) камеры, пикс. | 512 x 424 |
| Углы обзора RGB камеры, º | 84.1 x 53.8 |
| Углы обзора ИК камеры, º | 70.6 x 60.0 |
| Диапазон измерений дальности, м. | 0.6 — 8.0 1 |
| Частота съемки RGB камеры, Гц | 30 |
| Частота съемки ИК камеры, Гц | 30 |
Таким образом, передо мной стояли следующие задачи:
1. Kinect v2 и Python
Как я уже говорил, до этого я с компьютерным зрением дел не имел, но до меня доходили слухи, что без библиотеки OpenCV тут никуда. А поскольку в ней есть целый модуль для калибровки камер, то первым делом я собрал OpenCV с поддержкой Python 3 под Windows 8.1. Тут не обошлось без некоторой мороки, обычно сопровождающей сборку open-sourсe проектов на Windows, но все прошло без особых сюрпризов и в целом в рамках инструкции от разработчиков.
С Kinect-ом же пришлось повозиться несколько подольше. Официальный SDK поддерживает интерфейсы только для C#, С++ и JavaScript. Если зайти с другой стороны, то можно увидеть, что OpenCV поддерживает ввод с 3D камер, но камера должна быть совместима с библиотекой OpenNI. OpenNI поддерживает Kinect, а вот сравнительно недавний Kinect v2 — нет. Впрочем, добрые люди написали драйвер для Kinect v2 под OpenNI. Он даже работает и позволяет полюбоваться на видео с каналов устройства в NiViewer, но при использовании с OpenCV вылетает с ошибкой. Впрочем, другие добрые люди написали Python-обертку над официальным SDK. На ней я и остановился.
2. Калибровка камер
Камеры не идеальны, искажают картинку и нуждаются в калибровке. Чтобы использовать Kinect для измерений, было бы неплохо устранить эти геометрические искажения как на RGB камере, так и на датчике глубины. Поскольку ИК камера является одновременно и приемником датчика глубины, то мы можем использовать ИК кадры для калибровки, а затем результаты калибровки использовать для устранения искажений с кадров глубины.
Калибровка камеры осуществляется с целью узнать внутренние параметры камеры, а именно — матрицу камеры и коэффициенты дисторсии.
Матрицей камеры называется матрица вида:

(сu, cv) — координаты принципиальной точки (точки пересечения оптической оси с плоскостью изображения, в идеальной камере находиться точно в центре изображения, в реальных немного смещена от центра);
fu, fv — фокусное расстояние f, измеренное в ширине и высоте пикселя.
Существуют два основных вида дисторсии: радиальная дисторсия и тангенциальная дисторсия.
Радиальная дисторсия — искажение изображения в результате неидеальности параболической формы линзы. Искажения, вызванные радиальной дисторсией, равны 0 в оптическом центре сенсора и возрастают к краям. Как правило, радиальная дисторсия вносит наибольший вклад в искажение изображения.
Тангенциальная дисторсия — искажения изображения, вызванные погрешностями в установки линзы параллельно плоскости изображения.
Для устранение дисторсии координаты пикселей можно пересчитать с помощью следующего уравнения:
Точность измерения параметров камеры (коэффициенты дисторсии, матрица камеры) определяется средней величиной ошибки перепроэцирования (ReEr, Reprojection Error). ReEr — расстояние (в пикселях) между проекцией P’ на плоскость изображения точки P на поверхности объекта, и проекцией P» этой же точки P, построенной после устранения дисторсии с использованием параметров камеры.
Стандартная процедура калибровки камеры состоит из следующих шагов:
1) cделать 20-30 фотографий с разными положениями объекта с известной геометрией шахматной доски;
2) определить ключевые точки объекта на изображении;
3) найти такие коэффициенты дисторсии которые минимизирует ReEr.
В нашем случае, для RGB камеры среднее значение ReEr составило 0.3 пикселя, а для ИК камеры — 0.15. Результаты устранения дисторсии:
3. Совмещение кадров с двух камер
Для того чтобы получить для пикселя как глубину (Z координату), так и цвет, для начала необходимо перейти из пиксельных координат на кадре глубины в трехмерные координаты ИК камеры [2]:
где (x1,y1,z1) — координаты точки в системе координат ИК камеры,
z1 — результат возвращаемый датчиком глубины,
(u1,v1) — координаты пикселя на кадре глубины,
c1,u, c1,v — координаты оптического центра ИК камеры,
f1,u, f1,v — проекции фокусного расстояния ИК камеры.
Затем нужно перейти из системы координат ИК камеры к системе координат RGB камеры. Для этого требуется переместить начало координат с помощью вектора переноса T и повернуть систему координат с помощью матрицы вращения R:
После чего нужно перейти из трехмерной системы координат RGB камеры к пиксельным координатам RGB кадра:
Таким образом, после всех этих преобразований, мы можем получить для пикселя (u1, v1) кадра глубины значение цвета соответствующего пикселя RGB кадра (u2, v2).
Как видно на результирующей картинке, изображение местами двоится. Такой же эффект можно наблюдать и при использовании класса CoordinateMapper из официального SDK. Впрочем, если на изображении нас интересует только человек, то можно воспользоваться bodyIndexFrame (поток Kinect, позволяющий узнать, какие пиксели относятся к человеку, а какие к фону) для выделения области интереса и устранения двоения.
Для определения матрицы вращения R и вектора переноса T необходимо провести совместную калибровку двух камер. Для этого нужно сделать 20-30 фотографий объекта с известной геометрий в различных положениях как RGB, так и ИК камерой, лучше при этом не держать объект в руках, чтобы исключить возможность его смещения между снятием кадров разными камерами. Затем нужно воспользоваться функцией stereoCalibrate из библиотеки OpenCV. Данная функция определяет позицию каждой из камер относительно калибровочного объекта, а затем находит такое преобразование из системы координат первой камеры в систему координат второй камеры, которое обеспечивает минимизацию ReEr.
И в итоге мы получили ReEr = 0.23.
4. Калибровка канала глубины
Датчик глубины Kinect возвращает глубину (именно глубину, т.е. Z-координату, а не расстояние) в мм. Но насколько точны эти значения? Судя по публикации [2], ошибка может cоставлять 0.5-3 см в зависимости от дистанции, так что есть смысл провести калибровку канала глубины.
Эта процедура заключается в том, чтобы найти систематическую ошибку Kinect (разницу между эталонной глубиной и глубиной, выдаваемой сенсором) в зависимости от расстояния до объекта. А для этого необходимо знать эталонную глубину. Наиболее очевидный путь — расположить плоский объект параллельно плоскости камеры и измерить расстояние до него линейкой. Постепенно сдвигая объект и делая серию измерений на каждом расстоянии, можно найти среднюю ошибку для каждой из дистанций. Но, во-первых, это не очень удобно, во-вторых, найти идеально плоский объект относительно больших размеров и обеспечить параллельность его расположения относительно плоскости камеры сложнее, чем может показаться на первый взгляд. Поэтому в качестве эталона, относительно которого будет рассчитываться ошибка, мы решили взять глубину, определяемую по известной геометрии объекта.
Зная геометрию объекта (например размеры клеток шахматной доски) и расположив его строго параллельно плоскости камеры можно определить глубину до него следующим образом:
где f — фокусное расстояние,
d — расстояние между проекциями ключевых точек на матрице камеры,
D — расстояние между ключевыми точками объекта,
Z — расстояние от центра проекции камеры до объекта.
В случае если объект расположен не строго параллельно, а под некоторым углом к плоскости камеры, глубину можно определить на основе решения задачи Perspective-n-Point (PnP) [3]. Решению этой проблемы посвящен ряд алгоритмов, реализованных в библиотеке OpenCV, которые позволяют найти преобразование |R, T| между системой координат калибровочного объекта и системой координат камеры, а значит, и определить глубину с точностью до параметров камеры.
Для калибровки канала глубины мы произвели серию съемок калибровочного объекта на расстояниях
7 cм. Калибровочный объект располагался в центре кадра параллельно плоскости камеры, на сколько это возможно сделать «на глазок». На каждом расстоянии делался один снимок RGB камерой и 100 снимков датчиком глубины. Данные с датчика усреднялись, а расстояние, определенное по геометрии объекта на основе RGB кадра, принималось за эталон. Средняя ошибка в определении глубины датчиком Kinect на данной дистанции определилась следующем образом:
где z i RGB — расстояние до i-й ключевой точки по геометрии,
z i depth — усредненное по 100 кадрам расстояние до i-й ключевой точки по данным датчика глубины,
N — количество ключевых точек на объекте (в нашем случае 48).
Затем мы получили функцию ошибки от расстояния путем интерполяции полученных результатов.
На рисунке ниже показано распределение ошибок до и после коррекции на калибровочных кадрах. Всего было сделано 120000 измерений (25 дистанций, 100 кадров глубины на каждой, 48 ключевых точек на объекте). Ошибка до коррекции составила 17±9.95 мм (среднее ± стандартное отклонение), после — 0.45±8.16 мм.
Затем было сделано 25 тестовых кадров (RGB и глубина) калибровочного объекта в различных положениях. Всего 1200 измерений (25 кадров, 48 ключевых точек на каждом). Ошибка до коррекции составила 7.41±6.32 мм (среднее ± стандартное отклонение), после — 3.12±5.50 мм. На рисунке ниже представлено распределение ошибок до и после коррекции на тестовых кадрах.
Заключение
Таким образом, мы устранили геометрические искажения RGB камеры и датчика глубины, научились совмещать кадры и улучшили точность определения глубины. Код этого проекта можно найти тут. Надеюсь, он окажется небесполезным.
Исследование выполнено за счет гранта Российского научного фонда (проект №15-19-30012)
Калибровка камеры (Camera Calibration)
Tags: Калибровка камера матрица внешние внутренние параметры вращение перенос OpenCV искажения объектива шахматная доска Python
Введение
Калибровка — это процедура установления зависимости между входом (эталонные данные) и выходом (измеренные данные)
Калибровка камеры – это задача получения точных математических отношений между точками в 3D пространстве и их 2D проекциями на экране камеры. Цель процесса калибровки — найти матрицы внешних и внутренних параметров, а также коэффициенты радиальных и тангенциальных искажений объектива.
Одна из стандартных процедур калибровки камеры — это использование шаблона шахматной доски. Система координат камеры связывается с системой координат шахматной доски через распознавание углов клеток шахматной доски. По угловым точкам через решение системы уравнений определяются параметры калибровки.
Алгоритм калибровки одной камеры, а также алгоритм стереокалибровки реализован в библиотеке OpenCV.
Матрица внешних параметров
При калибровке внешние параметры определяют взаимное положение камеры и шахматной доски. Перед выводом зависимостей необходимо знать, как привязаны системы координат к этим элементам и какой из них подвижен.
На основе анализа результатов использования функций OpenCV определяем по элементам матрицы смещений, что СК камеры неподвижна, а шахматная доска перемещается относительно нее.
Оси X и Y направлены соответственно влево и вниз. Начало СК шахматной доски привязано к левой верхней вершине. Начало СК камеры находится в точке оптического центра (подробнее см. внутренние параметры камеры).
Для определения положения объекта в 3D пространстве достаточно 6 независимых параметров — 3 угла и 3 перемещения. Выбираем 6 удобных параметров и указываем с ними последовательность из 6 элементарных преобразований:
Для каждого из 6 преобразований запишем матрицы в однородных координатах :
Затем получаем композицию матриц, последовательно перемножая их.
Функция cv2.calibrateCamera выполняет основную задачу по калибровке. Она возвращает векторы поворота (3 * 1) и векторы переноса (3 × 1) калибровочного шаблона относительно камеры. Функция cv2.Rodrigues (rvec) преобразует вектор поворота в матрицу вращения. Функция np.concatenate((R_matrix, tvec), axis=1) объединяет матрицу вращения и вектор переноса в матрицу движения:
Сопоставляя элементы обоих матриц получаем 6 параметров:
Тестирую полученные выражения (программный код приводится ниже):
По модулю и по знаку углы beta, alpha и gamma соответствуют.
Сравниваю результаты для перемещений n, p и h с элементами матрицы смещений для того же фрейма (см. рисунок в начале подраздела).
Эти результаты также соответствуют.
Матрица внутренних параметров
Внутренние параметры определяют проективное преобразование от координат 3-D камеры в 2D координаты изображений в пиксельном представлении.
В матричном виде это преобразование записывается:
Положение точек снимка определяется в пиксельной системе координат uv, начало которой совмещено с верхним левым пикселем изображения.
Координаты центрального пикселя Cx и Cy (оптический центр) находятся на пересечении главной оптической оси объектива с матрицей камеры. Они также как и координаты любой другой точки на изображении определяются в пикселях — округляются с точностью до пикселя.
Посмотрим, как получена матрица внутренних параметров. Представим СК xyz, начало которой совпадает с фокусом камеры. Определим зависимости для проективного преобразования 3D координат xyz в 2D координаты изображения (uv) — в пиксельных единицах измерения:
пиксели в датчике изображения могут быть не квадратными, поэтому у нас два разных фокусных расстояния fx и fy.
Более простое для восприятия представление зависимостей:
Первые слагаемые в зависимостях для u и v округляются до целого.
В матричном виде зависимости запишутся:
Знак при координате y’ зависит от разновидности системы координат цифрового изображения. Различают две прямоугольных системы координат:
В фотограмметрии традиционно применяется левая СК (на рис. слева). В оконных WinAPI приложениях также используют эту систему координат. Правая СК (на рис. справа) принята при записи изображений в файл во всех форматах (включая и формат BMP файла). Для перехода из одной СК в другую достаточно выполнить преобразование v=H-u, где H — размер изображения в пикселях по вертикали.
Коэффициенты радиальных и тангенциальных искажений объектива
Существуют два основных вида дисторсии: радиальная дисторсия и тангенциальная дисторсия.
Радиальная дисторсия — искажение изображения в результате неидеальности параболической формы линзы. Искажения, вызванные радиальной дисторсией, равны 0 в оптическом центре сенсора и возрастают к краям. Как правило, радиальная дисторсия вносит наибольший вклад в искажение изображения.
Тангенциальная дисторсия — искажения изображения, вызванные погрешностями в установке линзы параллельно плоскости изображения.
Для устранения дисторсии координаты пикселей пересчитываются с помощью следующих уравнений:
Особенности калибровки камеры с помощью шахматной доски
Одна из стандартных процедур для вычисления всех неизвестных, указанных выше, или простой калибровки камеры — это использование шаблона шахматной доски. Система координат камеры связывается с системой координат шахматной доски через распознавание углов клеток шахматной доски (места, где два темных квадрата касаются друг друга).
Такие точки легко распознаются. OpenCV предоставляет ряд функций для калибровки камер использованием шаблона шахматной доски (см. Выполнение калибровки).
Можно скачать изображение шахматной доски, распечатать его на принтере и приклеить на жесткую плоскую поверхность — стекло, картон или фанеру. К подготовке шаблона необходимо подходить с особой тщательностью. Подробнее см. статью Калибровка монокулярной камеры и комментарии к статье Как проверить правильность калибровки вебкамеры?.
Если шахматная доска квадратная, то первая вершина однозначно не определена — может изменяться при повороте доски или камеры.
Подготовка изображений для калибровки
Итак, нам нужно выполнить калибровку Web-камеры, встроенной в notebook, по автоматически распознаваемым координатам вершин шахматной доски.
Мы должны заснять шахматную доску при разных ориентациях относительно Web-камеры. Можно зафиксировать камеру, а смещать шахматную доску. С точки зрения математики это одно и тоже.
Для подготовки изображений с Web-камеры ноутбука используем следующее Python приложение:
Запускаете приложение, ожидаете, пока включится камера. Выбираете ориентацию шахматной доски и нажимаете клавишу SPACE. В результате этого сохраняется png-файл изображения в директории проекта, где находится файл кода. Создайте несколько изображений (> 10) и нажмите клавишу ESC для выхода из программы.
Выбирайте ориентацию шахматной доски под наклоном и на расстоянии около 1м.
Выполнение калибровки
Создаем новый Python проект и помещаем изображения для калибровки камеры в папке frames — внутри проекта, там же, где и код приложения. Изображение для тестирования помещаем внутри проекта в папке frames_test.
Следующий Python код калибрует камеру по подготовленным изображениям и демонстрирует тестируемое изображение до и после калибровки:
Перед запуском программы обратите внимание, чтобы значение переменных boardWidth и boardHeight соответствовало количеству вершин шахматной доски. Если соответствия не будет, такие изображения программой игнорируются.
Функция cv2.calibrateCamera выполняет основную задачу по калибровке. Она оценивает внутренние и внешние параметры камеры для каждого из видов калибровочного шаблона. Алгоритм основан на A Flexible New Technique for Camera Calibration и Camera Calibration Toolbox for Matlab.
Для калибровки необходимо знать координаты точек 3D-объекта и определить соответствующие им 2D-проекции. Этого несложно добиться, используя объект с известной геометрией и легко обнаруживаемыми характерными точками. Такой объект называется калибровочным шаблоном, и OpenCV имеет встроенную поддержку шахматной доски в качестве такого шаблона (см. FindChessboardCorners).
rms, mtx, dist, rvecs, tvecs = cv2.calibrateCamera (objpoints, imgpoints, img_size,None,None)
Функция построена на итеративном алгоритме оптимизации. Алгоритм выполняет следующие шаги:
Функция возвращает окончательную ошибку повторного проецирования rms
found, rvec, tvec = cv2.solvePnP (objp, corners, mtx, dist)
где found — (True или False). Смысл других параметров функции solvePnP аналогичен функции calibrateCamera.
Логика использования этих функций следующая. При изменении положения камеры ее внутренние параметры сохраняются. Поэтому, можно сначала откалибровать внутренние параметры камеры с помощью calibrateCamera, а затем использовать функцию solvePnP для определения внешних параметров камеры по заданным внутренним параметрам и точкам всего лишь одного изображения.
Обратите внимание: если внутренние параметры известны, нет необходимости использовать эту функцию calibrateCamera только для оценки внешних параметров. Вместо этого используйте solvePnP.
Подобранные при калибровке коэффициенты дисторсии устраняют искажения только вокруг шахматной доски. За ее пределами искажения усиливаются — очевидно, это компенсация за выравнивание изображения вокруг шахматной доски. Изображение после калибровки может быть представлено обрезанным — удаляется часть рисунка с искажениями. Для этого значение 3-го параметра указанной ниже функции заменяется (с 1 на 0):
R_matrix, _ = cv2.Rodrigues (rvec)
Эта функция преобразует вектор поворота rvec (3 * 1), возвращаемый функциями calibrateCamera и solvePnP, в матрицу поворота (3 * 3). Кроме этого, вы можете объединить их в матрицу движения [R t]:
Точность калибровки
Точность калибровки камеры оценивается по среднеквадратичной ошибке (Root Mean Square Error, RMS Error, RMSE) перепроецирования точки.
Что такое ошибка перепроецирования точки? По положению точки, как минимум на двух изображениях камеры, вычисляются ее трехмерные координаты с использованием внутренних и внешних параметров камеры.
Как только трехмерные координаты точки вычислены, трехмерная точка повторно проецируется на все изображения, которые она появляется. Расстояние между отмеченной и перепроецированной точкой на одном изображении является ошибкой перепроецирования точки.
Функция cv2.calibrateCamera возвращает среднеквадратичную ошибку повторного проецирования (rms), обычно она должна находиться в пределах от 0.1 до 1.0 пикселя при хорошей калибровке.
Среднеквадратичная ошибка 1.0 означает, что в среднем каждая из перепроецируемых точек (Reprojected point) находится на расстоянии 1.0 пикселя от своего фактического положения (3D point, marked on the image).
Rms находится через решение задачи оптимизации — определяется набор параметров (cameraMatrix, distCoeffs, rvecs и tvecs), который минимизирует rms итеративно.




































