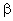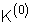что такое изохронные кривые

Большая Энциклопедия Нефти и Газа

Изохронная кривая

Изохронные кривые для данного полуцикла деформирования зависят от предыстории циклического нагружения, которая проявляется прежде всего через функцию общего времени деформирования, учитывающую частоту активного нагружения, а также наличие или отсутствие выдержек. [1]

Схема изохронных кривых статической ползучести показана на рис. 4.7, а. Изохронные кривые циклического деформирования ( повторное нагру-жение в сочетании с ползучестью при выдержке под нагрузкой) показаны на рис. 4.7, в. Изохронные кривые для данного полуцикла деформирования зависят от режима предыдущего циклического нагружения, что проявляется прежде всего через функцию общего времени деформирования, учитывающую частоту активного нагружения, а также выдержку. [4]

Схема изохронных кривых статической ползучести показана на рис. 2.3.12, а, причем т 0 соответствует мгновенной статической кривой, все другие кривые представляют собой изохронные кривые ползучести. Приведено семейство мгновенных кривых циклического деформирования ( т 0), что соответствует случаю отсутствия ползучести. [5]

Преобразование подобия для изоциклических и изохронных кривых осуществляется с помощью функций подобия по числу циклов и по времени. Эти функции и их параметры определяются из системы базовых экспериментов, выполняемых при мягком нагру-жении с выдержками и без выдержек при различных уровнях амплитуд напряжений с варьируемыми скоростями деформирования и временами выдержек в цикле. [8]

Расчет ведется по изохронным кривым ползучести в разное время нагружения. [10]

Наблюдаемые расхождения между изохронными кривыми ползучести для простого и плоских напряженных состояний вызваны, по-видимому, некоторой начальной анизотропией образцов, изготовленных из экструзионных труб. [12]

Данные расчета с использованием изохронных кривых ( рис. 5.22) показывают, что изменение напряжений с течением времени существенно замедляется. [14]

Ранее было отмечено, что изохронные кривые могут быть описаны различными функциями нелинейности. [15]

Источник

Временные уравнения состояния и критерии длительной прочности

Вязкие (или реологические) свойства твердых тел устанавливаются главным образом по данным опытов на ползучесть. Ползучестьюназывается накапливание деформации во времени при постоянном напряжении.

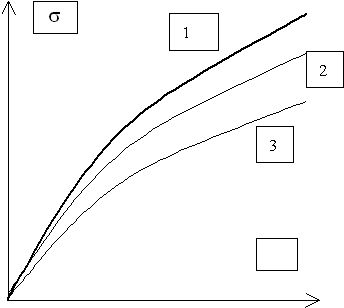
Рис. 22. Общий вид кривой ползучести

На рис. 22 показана типичная кривая ползучести при фиксированном эффективном напряжении сжатия (или растяжения) и определенных внешних условиях (температура, давление, влажность). На этой кривой выделяют условно три стадии ползучести:

АВ – неустановившаяся, она характеризуется уменьшением скорости деформации;

ВС – установившаяся, скорость постоянная;

СД – прогрессирующая, скорость деформации растет вплоть до момента разрушения.

Деформация образца на первом участке сопровождается структурными изменениями, которые затрудняют ползучесть, происходит упрочнение. Выход на участок ВС означает, что материал исчерпал способность упрочняться, и вследствие этого уменьшилась скорость деформации. Ускоренная ползучесть на участке СД объясняется зарождением и развитием трещин. Участок вертикальной оси 0А соответствует мгновенной деформации , коротая в зависимости от уровня напряжения может быть либо упругой, либо содержать мгновенную пластическую деформацию. В любой момент времени полную накопленную деформацию можно определить в виде суммы , где — деформация ползучести.

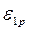
Рис. 23. Серия кривых ползучестиРис. 24. Семейство изохронных

1. Теория старения.Для описания участков кривой ползучести используются различные теории (гипотезы). Так, для описания первых двух участков кривой чаще других используется теория старения, согласно которой полная деформация является функцией напряжения и времени при фиксированных внешний условиях (давление, температура, влажность и т.д.), т.е. . Эта функция задается серией кривых ползучести, которые затем перестраиваются в изохронные кривые в координатах . Техника подобной перестройки очевидна. Проведем вертикальную прямую, соответствующую . Точки пересечения этой прямой с кривыми ползучести определяют пары значений и . Построив их в соответствующей системе координат, получим кривую для момента времени . Подобным образом строятся кривые для других моментов времени. Эту серию кривых называют семейством изохронных кривых. Кривая мгновенного деформирования (t = 0) также является изохронной.

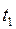
Экспериментально установлено, что совокупность изохронных кривых можно описать с помощью следующей эмпирической формулы

, (2.83)

где — параметры ползучести.

Для вязкопластичного тела функция нелинейная, определяется согласно (2.68). Для вязкоупругого тела , и с учетом (2.83) деформацию вычисляют по формуле

. (2.84)

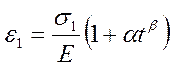
Рис. 25. К определению параметров ползучести

а – деформационная кривая; б – исходная кривая по ползучести; в – преобразованная кривая по текучести

.

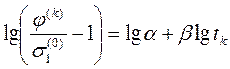
Откуда — величина отрезка, отсекаемого построенной прямой на оси ординат, а — ее угловой коэффициент. Естественно, более точные результаты получатся, если использовать несколько кривых ползучести.

Характерно, что параметр близок к 0,3 для различных горных пород.

По теории старения для описания сложного напряженного состояния

пользуются теми же уравнениями обобщенного закона Гука [см формулу (2.73)], в которых надо модули упругости G и пластичности заменить функциями времени и соответственно.

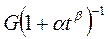
Ниже приведены средние значения параметров и для некоторых горных пород при времени, заданном в с.

коэффициенты
Песчаник	0,0046	0,283
Известняк	0,0067	0,299
Глина кембрийская	0,01	0,2
Аргеллит	0,0158	0,279
Алевролит	0,0368	0,285
Галит	0,085	0,2
Каменная соль	0,15	0,246

Благодаря простоте и удобству, теория старения нашла широкое применение в практике инженерных расчетов. Но в силу того, что эта теория исходит из опытов на ползучесть при постоянных нагрузках, ею можно пользоваться только в условиях постоянства напряженного состояния или медленного монотонного его изменения.

Для общего случая действия нагрузки на твердое тело используют уравнения состояния хорошо разработанной теории наследственной ползучести.

Источник

Что такое изохронные кривые

Наиболее простой теорией ползучести является теория старения. В соответствии с этой теорией должна существовать зависимость

где — суммарная деформация и напряжение при простом растяжении, t и Т — время и температура нагружения. В соответствии с равенством (94) суммарная деформация

Для сложного напряженного состояния зависимость (96) относится к интенсивностям деформаций и напряжений:

или в другой форме

Интенсивность суммарной деформации (упругости, пластичности и ползучести) определяется интенсивностью напряжений, временем и температурой нагружения.

Для стационарного режима нагружения ) зависимость

может быть определена из эксперимента (кривых ползучести). Основная гипотеза теории старения состоит в том, что зависимость (99) справедлива при нестационарном нагружении

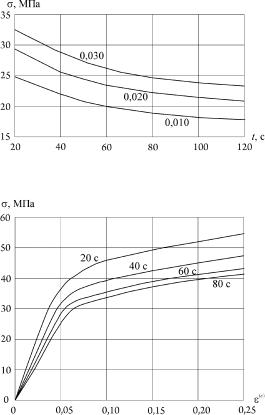
Расчет ползучести основывается на кривых ползучести (см. разд. 15), построенных при постоянных температурах для различного уровня напряжений. На рис. 5.17 показана сетка кривых ползучести при напряжениях

По оси абсцисс откладывается время, по оси ординат — деформация при растяжении стержня (образца) при постоянном напряжении. В момент (начало отсчета) начальная деформация соответствует мгновенной деформации (упругой или упругопластической) в результате действия приложенного напряжения.

Рис. 5.17. Построение изохронных кривых ползучести (б) по сетке кривых ползучести (а)

при построении кривых ползучести так же, как и кривых деформирования, не учитывается.

Если провести сечение , например то прямая пересечет кривые ползучести в точках которым соответствуют деформации ползучести .

В каждой точке известно значение действующего напряжения Эти данные позволяют построить зависимость

На рис. 5.17 кривая (101) проходит через точки Зависимость (101) выражает изохронную кривую ползучести для времени t.

Для начального значения времени t = 0 изохронная кривая совпадает с обычной кривой деформирования при растяжении стержня. Сетку кривых деформирования можно представить в виде поверхности суммарных деформаций при ползучести (рис. 5.18) в координатах

Плоскости (на рис. 5.18 они заштрихованы) при пересечении с поверхностью образуют изохронные кривые ползучести.

Рис. 5.18. Поверхность суммарных деформаций при ползучести

По теории старения, которая излагается в трактовке Ю. Н. Работнова, ползучесть приводит к уменьшению упругопластического сопротивления материалов — с увеличением времени условные кривые деформирования понижаются, материал «состаривается».

Отметим, что деформации ползучести возникают и при напряжениях, меньших предела текучести, и потому «понижение» происходит и на упругом участке условных кривых деформирования.

После нахождения изохронных кривых ползучести задача сводится к расчету упругопластического тела по деформационной теории пластичности (разд. 19). Для начального момента времени расчет полностью совпадает с определением напряжений деформаций по деформационной теории пластичности.

Для момента времени t проводится точно такой же расчет, но в качестве кривой деформирования принимается изохронная кривая ползучести для соответствующего момента времени.

Модели ползучести, основанные на теории старения, пригодны для описания монотонного, или стационарного, нагружения, процессов релаксации (падения) напряжений при неизменной деформации.

Основным недостатком теории старения является отрицание влияния истории нагружения. Из уравнения (98) следует, что в момент времени t данному напряжению соответствует определенная деформация ползучести. Следовательно, если напряжение мгновенно возрастет, то должна мгновенно увеличиться и деформация ползучести, что, конечно, произойти не может.

Более правильно считать, как это делается в других теориях ползучести, что при мгновенном возрастании напряжений подобным образом увеличивается скорость ползучести.

Источник

6. ОСНОВНЫЕ МОДЕЛИ ПОЛЗУЧЕСТИ

рость ( c ) = d » ( c ) = d » деформации ползучести » ( c ) постепенно dt dt

Основные модели ползучести

В этом случае при «, T = const функция 1 ( t ) описывает релаксацию. Для многих конструкционных материалов можно принять

Основные модели ползучести

здесь функцию ( t ) определим соотношением

С другой стороны, из соотношения для » ( c ) можно получить

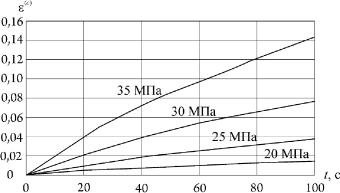
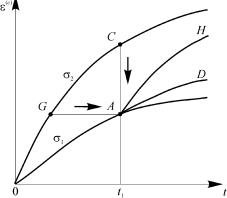
Последнее соотношение можно использовать и для построения семейства изохронных кривых ползучести, если менять значения деформации ползучести, но при этом зафиксировать определенные моменты времени, например, 20 с, 40 с, 60 с, 80 с. Графики изохронных кривых ползучести показаны на рис. 6.4.

Основные модели ползучести

Так как все изохронные кривые выходят из начала системы координат O «, то, согласно теории старения, после накопления некоторой деформации ползучести » ( c ) при разгрузке до = 0 эта деформация должна полностью исчезнуть, что часто противоречит экспериментальным результатам. От такого противоречия свободна ММ, базирующаяся на теории течения и постулирующая существование зависимости

Основные модели ползучести

Эту зависимость часто удается представить в виде

что при постоянных и T после интегрирования по t позволяет получить соотношение

При изменении знака вместо » ( c ) в качестве аргумента следует использовать параметр

Основные модели ползучести

Учет предыстории процесса ползучести может быть также проведен в рамках так называемой наследственной теории ползучести.

За время t 1 деформация ползучести достигает величины » ( A c ) (см. рис. 6.5), здесь точка A является точкой пересечения вертикальной линии, проведенной на расстоянии t 1 от оси ординат

Основные модели ползучести

Обобщение рассмотренных ММ ползучести при одноосном напряженном состоянии на случай сложного напряженного состояния можно провести на основе следующих допущений.

Основные модели ползучести

3. Компоненты » ( ij c ) (в случае теории старения) и ij ( c ) (в остальных случаях) пропорциональны компонентам s ij девиатора напряжений.

Эти допущения позволяют для теорий старения, течения и упрочнения соответственно записать

Источник

УДК 539.4

Прикладная математика и механика

Харьковский государственный технический университет строительства и архитектуры. 61002. Харьков.

Особенности применения принципа подобия кривых ползучести в теории неравновесных деформационных процессов

Построение универсальной относительно различных режимов нагружения связи между макропараметрами модели сплошной среды (напряжений, деформаций, скоростей деформации и температуры) основано на гипотезе о существовании уравнения состояния при равной нулю скорости деформации, или кинетического уравнения в противном случае. Его, обычно, не удается реализовать, так как сплошную среду принято рассматривать как одноуровневую систему, тогда как реальные материалы являются многоуровневыми иерархическими системами. На одних иерархических уровнях равновесное состояние достигается быстро, о чем свидетельствует обращение в ноль скорости деформации, а на других уровнях процесс деформации на протяжении длительного времени продолжается с конечной скоростью деформации [ 1 ], [ 2 ]. Определяющие уравнения, отображающие сигналы на входе (область определения) на сигналы на выходе (область значений), могут быть представлены в виде функции, функционала, или оператора. При постоянной температуре для равной нулю скорости деформации связь между напряжениями и деформациями при одноосном напряженном состоянии может быть описана функцией. Для измерения равновесной деформационной кривой требуется затратить много средств и времени, поэтому она измеряется не в прямых опытах, а косвенными методами. В случае постоянной температуры, но отличной от нуля скорости деформации связь между напряжениями и деформациями, имеющая вид функционала, также не может быть построена, так как задача построения функционала по результатам испытаний конечного числа образцов материала не поставлена математически.

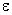
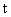
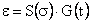
Ю.Н. Работновым предложено использовать зависимость деформации от времени в виде произведения

(1.2)

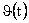
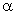
Для наглядности, но не для обоснования Ю.Н. Работнов использовал понятие о мгновенных деформационных кривых, записав функцию с некоторыми постоянными коэффициентами и

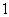
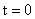
Мгновенной деформационной кривой ( ) на рис.1 при соответствует не зависящее от времени базовое выражение

С известной долей погрешности в рамках приближенного подхода принцип подобия кривых ползучести, описываемых выражением (1.2), и деформационных кривых, описываемых формулой (1.3), нашел экспериментальное подтверждение и даже стал применяться для сравнения между собой различных технических теорий изотермической ползучести в форме старения

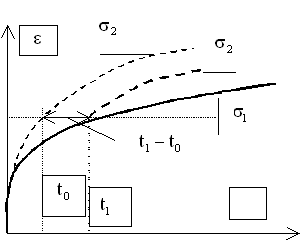
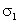
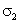
Рис.2. Иллюстрация применения принципа подобия кривых ползучести по Ю.Н. Работнову. Скачок напряжения от до сопровождается скачком скорости деформации до величины, равной угловому коэффициенту касательной к верхней кривой ползучести в «точке, имеющей ту же ординату».

В приведенных рассуждениях Ю.Н. Работнова учитывается только одно из двух возможных правил выбора точки на верхней кривой ползучести, где вычисляется скорость. Вместо слов « в точке, имеющей ту же ординату» можно говорить о « точке, имеющей ту же абсциссу». Очевидно, что Ю.Н. Работнов выбрал не лучший вариант, говоря о той же ординате, так как приравнивание скоростей по ординате соответствует первой ( time hardening ) теории. 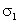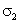Более точной второй ( strain hardening ) теории упрочнения соответствовала бы фраза: «Скачок напряжения от до сопровождается скачком скорости деформации до величины, равной угловому коэффициенту касательной к верхней кривой ползучести в «точке, имеющей ту же абсциссу».

С учетом указанных недостатков в рассуждениях Ю.Н. Работнова в данной работе для описания зависимости деформации ползучести от времени при постоянном напряжении используются две группы уравнений: уравнение состояния на мезоуровне, формулируемое в равновесных напряжениях и деформациях и кинетическое уравнение, устанавливающее связь между параметрами состояния мезо и макроуровня. Из уравнения состояния и кинетического уравнения следуют технические теории изотермической ползучести, а принцип подобия кривых ползучести является следствием уравнения состояния на мезоуровне, описывающего равновесный процесс деформационного упрочнения. Время в уравнении ползучести появляется в результате интегрирования кинетического уравнения при заданном режиме изменения нагрузки, т.е. уравнения теории старения описывают траекторию процесса деформации в конкретных условиях.

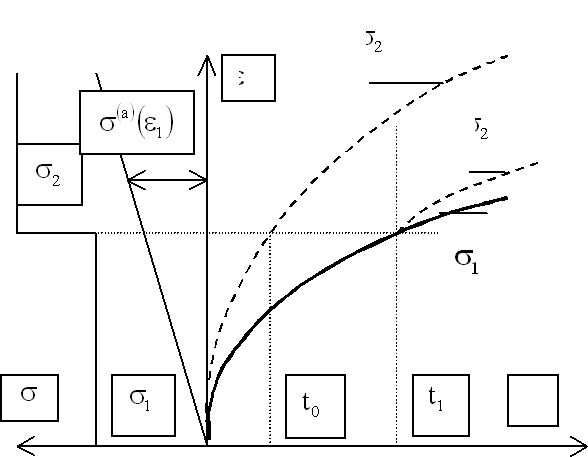
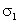
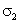
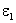
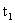
Рис. 3. Иллюстрация применения принципа подобия кривых изотермической ползучести при ступенчатом изменении нагрузки. Скачок напряжения от до при деформации сопровождается скачком скорости деформации до величины, равной угловому коэффициенту касательной к верхней кривой ползучести в «точке, имеющей ту же абсциссу – время ». На величину скорости деформации оказывает влияние эффективное напряжение.

Процесс сопротивления деформации материала как иерархической системы рассматривается в фазовом пространстве равновесных напряжений на мезо и макроуровнях. На рис. 3 график уравнения состояния представлен линейной зависимостью равновесных напряжений от деформации ползучести. Гипотеза о полилинейной формы записи уравнения состояния на мезоуровне предложена новая формулировка принципа подобия кривых ползучести, позволяющая описать зависимость деформации от времени при ступенчатом изменении нагрузки.

2. Параметры состояния иерархической системы

(2.1)

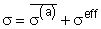
3. Кинетическое уравнение сопротивления деформации ползучести

Связь между параметрами состояния мезо и макроурвней при изотермической ползучести устанавливает кинетическое уравнение [2], записанное в безразмерном и универсальном для различных материалов виде

4. Уравнение состояния на мезоуровне

Уравнение состояния на мезоуровне, описывающее равновесную деформационную кривую, с помощью нелинейных

(4.1)

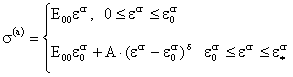
или кусочно-линейных функций

Здесь приняты следующие обозначения

(4.3)

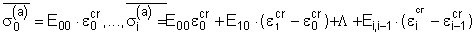
5. Интегрирование кинетического уравнения при ступенчатом изменении нагрузки в случае полилинейного уравнения состояния

В случае полилинейной формы записи уравнения состояния (4.2) при заданном ступенчатом изменении нагрузки

(5.1)

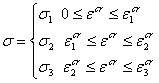
может быть получено решение кинетического уравнения

(5.2)

в неявном относительно виде:

(5.3)

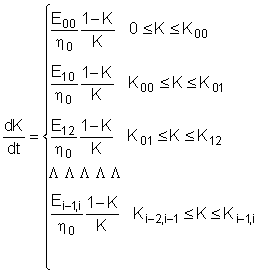
6. Представление решения кинетического уравнения в явном относительно K виде

Пусть на основе неявного относительно 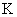задания решения конститутивного уравнения

требуется построить его приближенное выражение в явном виде, используя разложение логарифма в ряд и ограничившись первыми двумя членами

Тогда, с учетом разложения (5.2) соотношение (5.1) упрощается

(6.3)

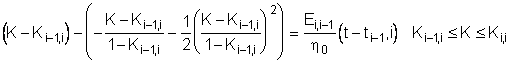
и может быть решено относительно переменной

(6.4)

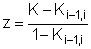
С учетом полученного приближенного решения

(6.6)

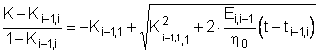
можно записать нулевое

первое

и второе

(6.9)

приближения, подставив в формулу требуемое выражение К

Можно также воспользоваться приближенными явными зависимости К( t ) в нулевом,

(6.11)

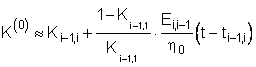
и в первом приближениях

(6.12)

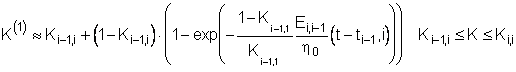
Смысл нулевого приближения очевиден

Для первого приближения допустима следующая интерпретация:

При ступенчатом изменении нагрузки приращение деформации ползучести на каждом отрезке времени, где уровень напряжения фиксирован, определяется произведением скорости деформации ползучести в момент времени 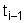на функцию влияния

7. Плотность распределения элементов структуры по равновесным напряжениям

(7.1)

(7.2)

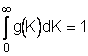
Величины параметров, входящих в формулу (7.1), определяются по результатам макро опытов. Возможность построения распределения элементов дискретной структуры на мезоуровне по результатам макро опытов служит еще одним подтверждением известного принципа макро определимости, имеющим вероятностную форму, из которой следует также определимость вероятности разрушения.

8. Вероятности разрушения элементов структуры на мезоуровне.

Функция 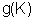плотности распределения элементов структуры по равновесным напряжениям, удовлетворяющая стационарному уравнению Фоккера Планка

определяет вероятность разрушения на мезо уровне

(8.2)

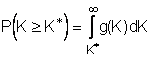
9. Первичные кривые изотермической ползучести титанового сплава при постоянных напряжениях

(9.1)

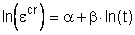
с наклоном b к оси 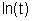и постоянной a при заданной величине напряжения; значения коэффициентов a и b уравнения (9.1) указаны в табл. 1.

Таблица 1

Значения коэффициентов уравнения (9.1) для титанового сплава

Источник