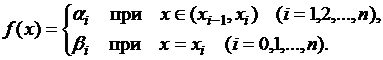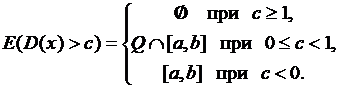что такое измеримая функция

§ 5. Измеримые функции. Примеры

3) Ступенчатая на данном сегменте функция является измеримой на нем.

Тогда ясно, что при множество либо пусто, либо представляет собой объединение конечного числа промежутков, т.е. является элементарным множеством. Все элементарные множества являются измеримыми, поэтому любая ступенчатая функция является измеримой.

Заметим, что ступенчатая функция может иметь точки разрыва. Значит, разрывные функции могут быть измеримыми.

4) Легко проверить, что функция на сегменте измерима.

6) Функция Дирихле 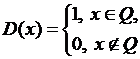измерима на любом сегменте (хотя все точки этого отрезка ( при ) являются точками разрыва этой функции).

Получили всего три вида измеримых множеств, а поэтому функция Дирихле также измерима.

Значит, всюду разрывная на данном промежутке функция может быть измеримой на нем.

Изучая вопросы обратимости утверждения 7), Н. Н. Лузин доказал, что измеримая на сегменте функция становится непрерывной, если изменить ее значения на множестве сколь угодно малой меры.

Источник

Измеримая функция

Измери́мые функции представляют естественный класс функций, связывающих пространства с выделенными алгебрами, в частности измеримыми пространствами.

Содержание

Определение

Пусть и — два множества с выделенными алгебрами подмножеств. Тогда функция называется —измеримой, или просто измеримой, если полный прообраз любого множества из принадлежит , то есть

где означает полный прообраз множества .

Замечания

Вещественнозначные измеримые функции

Пусть дана функция . Тогда данное выше определение измеримости эквивалентно любому из нижеследующих:

где обозначает любой интервал, открытый, полуоткрытый или замкнутый.

Связанные определения

Примеры

История

В 1901 году французский математик Лебег, на основе построенной им теории интеграла Лебега, поставил задачу: найти класс функций, более широкий, чем аналитические, однако при этом допускающий применение к нему многих аналитических методов. К этому времени уже существовала общая теория меры, разработанная Э. Борелем (1898), и первые работы Лебега опирались на борелевскую теорию. Однако в диссертации Лебега (1902) теория меры была существенно обобщена до «меры Лебега». Лебег определил понятия измеримых множеств, ограниченных измеримых функций и интегралов для них, доказал, что все «обычные» ограниченные функции, исследуемые в анализе, измеримы, и что класс измеримых функций замкнут относительно основных аналитических операций, включая операцию предельного перехода. В 1904 году Лебег обобщил свою теорию, сняв условие ограниченности функции.

Исследования Лебега нашли широкий научный отклик, их продолжили и развили многие математики: Э Борель, М. Рисс, Дж. Витали, М. Р. Фреше, Н. Н. Лузин, Д. Ф. Егоров и др. Было введено понятие сходимости по мере (1909), глубоко исследованы топологические свойства класса измеримых функций.

Труды Лебега имели ещё одно важное концептуальное значение: они были полностью основаны на спорной в те годы канторовской теории множеств, и плодотворность лебеговской теории послужила веским аргументом для принятия теории множеств как фундамента математики.

Литература

Полезное

Смотреть что такое «Измеримая функция» в других словарях:

ИЗМЕРИМАЯ ФУНКЦИЯ — 1) В первоначальном понимании И. ф. функция f(x)действительного переменного, обладающая тем свойством, что для любого амножество Е а точек х, для к рых f(x)Математическая энциклопедия

Функция (математ.) — Функция, одно из основных понятий математики, выражающее зависимость одних переменных величин от других. Если величины x и у связаны так, что каждому значению x соответствует определённое значение у, то у называют (однозначной) функцией аргумента … Большая советская энциклопедия

Функция — I Функция (от лат. functio совершение, исполнение) (философская), отношение двух (группы) объектов, в котором изменение одного из них ведёт к изменению другого. Ф. может рассматриваться с точки зрения следствий (благоприятных,… … Большая советская энциклопедия

Суммируемая функция — функция, к которой приложимо введённое А. Лебегом понятие Интеграла, то есть для которой интеграл Лебега, взятый по данному множеству, конечен. Функции эти, называемые также интегрируемыми по Лебегу, необходимо должны быть измеримыми (по… … Большая советская энциклопедия

Статистика (функция выборки) — У этого термина существуют и другие значения, см. Статистика (значения). Статистика (в узком смысле) это измеримая числовая функция от выборки, не зависящая от неизвестных параметров распределения. В широком смысле термин (математическая)… … Википедия

БОРЕЛЕВСКАЯ ФУНКЦИЯ — В функция, функция, для к рой все подмножества вида ) из области ее определения являются борелевскими множествами. Другие назв. Б. ф.: функции, измеримые по Борелю, В измеримые функции. Операции сложения, умножения и предельного перехода, как и в … Математическая энциклопедия

КРИТИЧЕСКАЯ ФУНКЦИЯ — статистика, значения к рой суть условные вероятности отклонения проверяемой гипотезы при заданном значении результата наблюдения. Пусть X случайная величина, принимающая значения в выборочном пространстве распределение вероятностей к рой… … Математическая энциклопедия

ЭКСЦЕССИВНАЯ ФУНКЦИЯ — для марковского процесса аналог неотрицательной супергармонической функции. Пусть в измеримом пространстве задана однородная марковская цепь с вероятностями перехода за один шаг Измеримая относительно функция наз. эксцессивной функцией для этой… … Математическая энциклопедия

Источник

Определение измеримой функции

[math] X = \bigcup\limits_p X_p : \mu X_p \lt + \infty [/math]

[math]E(f\lt a) = \left\ < \beginE &, C \lt a \\ \varnothing &, C \geq a \end \right. [/math]

Так как [math]E[/math] измеримо, то постоянная функция на нём измерима.

Проверим, что оно замкнуто.

Множество содержит в себе пределы всех сходящихся подпоследовательностей, то есть замкнуто. Но, как было установлено ранее, замкнутые множества измеримы по Лебегу.

Вывод: класс непрерывных функций содержится в классе измеримых.

1) [math]|f|[/math] — измерим
1.5) [math]kf[/math] — измерима ( [math]k \in \mathbb[/math] )
2) [math]f^2[/math] — измерим
3) [math]f + g[/math] — измерима

4) [math]f \cdot g[/math] — измеримо

Это пересечение двух измеримых множеств Лебега [math]\Rightarrow[/math] измеримо.

3) Доказывается чуть сложнее

Источник

ИЗМЕРИМАЯ ФУНКЦИЯ

2) И. ф. на пространстве Xопределяется относительно выбранной системы измеримых множеств Ав X. Если A есть s-кольцо, то действительная функция f, заданная на пространстве X, наз. измеримой функцией, если

для любого действительного а, где

Лит.:[1] Xалмош П., Теория меры, пер. с англ.,М. 1953; [2] Данфорд Н., Шварц Д ж. Т., Линейные операторы, пер. с англ., т. 1, М., 1962; [3] Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 4 изд., М., 1976.

Полезное

Смотреть что такое «ИЗМЕРИМАЯ ФУНКЦИЯ» в других словарях:

Измеримая функция — Измеримые функции представляют естественный класс функций, связывающих пространства с выделенными алгебрами, в частности измеримыми пространствами. Содержание 1 Определение 2 Замечания … Википедия

Функция (математ.) — Функция, одно из основных понятий математики, выражающее зависимость одних переменных величин от других. Если величины x и у связаны так, что каждому значению x соответствует определённое значение у, то у называют (однозначной) функцией аргумента … Большая советская энциклопедия

Функция — I Функция (от лат. functio совершение, исполнение) (философская), отношение двух (группы) объектов, в котором изменение одного из них ведёт к изменению другого. Ф. может рассматриваться с точки зрения следствий (благоприятных,… … Большая советская энциклопедия

Суммируемая функция — функция, к которой приложимо введённое А. Лебегом понятие Интеграла, то есть для которой интеграл Лебега, взятый по данному множеству, конечен. Функции эти, называемые также интегрируемыми по Лебегу, необходимо должны быть измеримыми (по… … Большая советская энциклопедия

Статистика (функция выборки) — У этого термина существуют и другие значения, см. Статистика (значения). Статистика (в узком смысле) это измеримая числовая функция от выборки, не зависящая от неизвестных параметров распределения. В широком смысле термин (математическая)… … Википедия

БОРЕЛЕВСКАЯ ФУНКЦИЯ — В функция, функция, для к рой все подмножества вида ) из области ее определения являются борелевскими множествами. Другие назв. Б. ф.: функции, измеримые по Борелю, В измеримые функции. Операции сложения, умножения и предельного перехода, как и в … Математическая энциклопедия

КРИТИЧЕСКАЯ ФУНКЦИЯ — статистика, значения к рой суть условные вероятности отклонения проверяемой гипотезы при заданном значении результата наблюдения. Пусть X случайная величина, принимающая значения в выборочном пространстве распределение вероятностей к рой… … Математическая энциклопедия

ЭКСЦЕССИВНАЯ ФУНКЦИЯ — для марковского процесса аналог неотрицательной супергармонической функции. Пусть в измеримом пространстве задана однородная марковская цепь с вероятностями перехода за один шаг Измеримая относительно функция наз. эксцессивной функцией для этой… … Математическая энциклопедия

Источник