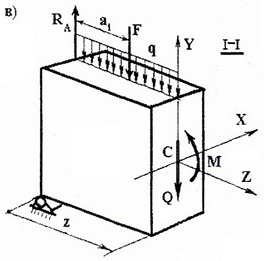
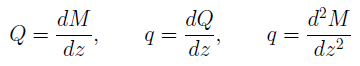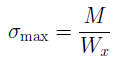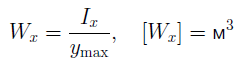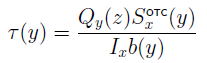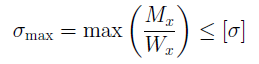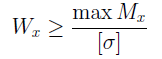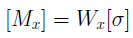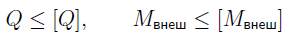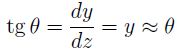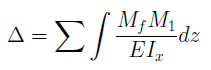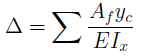что такое изгиб сопромат
Изгиб.
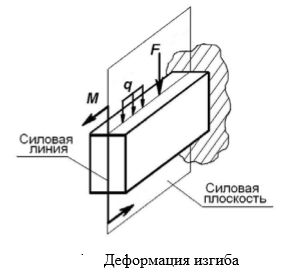
Изгибом называется вид деформации, при котором искривляется продольная ось бруса. Прямые брусья, работающие на изгиб, называются балками. Прямым изгибом называется изгиб, при котором внешние силы, действующие на балку, лежат в одной плоскости (силовой плоскости), проходящей через продольную ось балки и главную центральную ось инерции поперечного сечения.
Внутренние силовые факторы при изгибе балки.
При плоском поперечном изгибе в сечениях балки возникают два внутренних силовых фактора: поперечная сила Q и изгибающий момент М. Для их определения используют метод сечений (см. лекцию 1). Поперечная сила Q в сечении балки равна алгебраической сумме проекций на плоскость сечения всех внешних сил, действующих по одну сторону от рассматриваемого сечения.
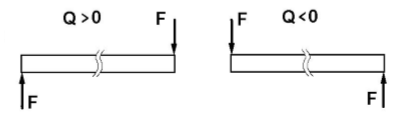
Правило знаков для поперечных сил Q:
Изгибающий момент М в сечении балки равен алгебраической сумме моментов относительно центра тяжести этого сечения всех внешних сил, действующих по одну сторону от рассматриваемого сечения.
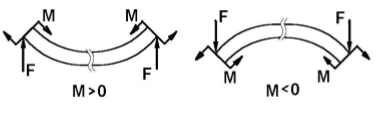
Правило знаков для изгибающих моментов M:
Дифференциальные зависимости Журавского.
Между интенсивностью q распределенной нагрузки, выражениями для поперечной силы Q и изгибающего момента М установлены дифференциальные зависимости:
На основе этих зависимостей можно выделить следующие общие закономерности эпюр поперечных сил Q и изгибающих моментов М:
Особенности эпюр внутренних силовых факторов при изгибе.
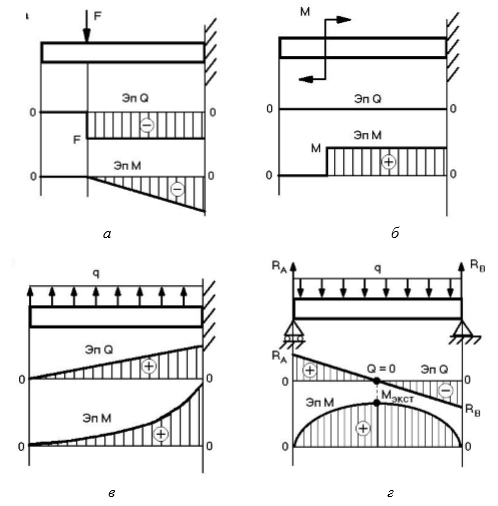
1. На участке балки, где нет распределенной нагрузки, эпюра Q представлена прямой линией, параллельной базе эпюре, а эпюра М — наклонной прямой (рис. а).
3. В сечении, где приложен сосредоточенный момент, значение Q не изменяется, а эпюра М имеет скачок, равный значению этого момента, (рис. 26, б).
4. На участке балки с распределенной нагрузкой интенсивности q эпюра Q изменяется по линейному закону, а эпюра М — по параболическому, причем выпуклость параболы направлена навстречу направлению распределенной нагрузки (рис. в, г).
5. Если в пределах характерного участка эпюра Q пересекает базу эпюры, то в сечении, где Q = 0, изгибающий момент имеет экстремальное значение Mmax или Mmin (рис. г).
Нормальные напряжения при изгибе.
Определяются по формуле:
Моментом сопротивления сечения изгибу называется величина:
Опасным сечением при изгибе называется поперечное сечение бруса, в котором возникает максимальное нормальное напряжение.
Касательные напряжения при прямом изгибе.
Определяются по формуле Журавского для касательных напряжений при прямом изгибе балки:
Расчеты на прочность при изгибе.
1. При проверочном расчете определяется максимальное расчетное напряжение, которое сравнивается с допускаемым напряжением:
2. При проектном расчете подбор сечения бруса производится из условия:
3. При определении допускаемой нагрузки допускаемый изгибающий момент определяется из условия:
Далее по полученному значению [Mx] определяют допускаемые значения внешних поперечных нагрузок [Q] и внешних изгибающих моментов [Mвнеш]. Условие прочности имеет вид:
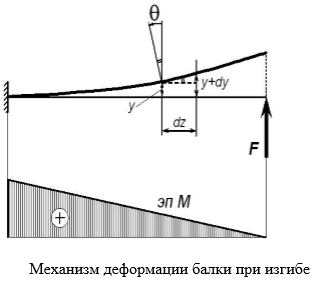
Перемещения при изгибе.
Прогиб считают положительным, если перемещение центра тяжести происходит вверх. Величина прогиба меняется по длине балки, т.е. y = y (z)
Самыми распространёнными способами определения перемещений является метод Мора и правило Верещагина.
Метод Мора.
Порядок определения перемещений по методу Мора:
1. Строится «вспомогательная система» и нагружается единичной нагрузкой в точке, где требуется определить перемещение. Если определяется линейное перемещение, то в его направлении прикладывается единичная сила, при определении угловых перемещений – единичный момент.
3. По всем участкам системы вычисляют и суммируют интегралы Мора, получая в результате искомое перемещение:
4. Если вычисленное перемещение имеет положительный знак, то это значит, что его направление совпадает с направлением единичной силы. Отрицательный знак указывает на то, что действительное перемещение противоположно направлению единичной силы.
Правило Верещагина.
Для случая, когда эпюра изгибающих моментов от заданной нагрузки имеет произвольное, а от единичной нагрузки – прямолинейное очертание, удобно использовать графоаналитический способ, или правило Верещагина.
где Af – площадь эпюры изгибающего момента Мf от заданной нагрузки; yc – ордината эпюры от единичной нагрузки под центром тяжести эпюры Мf ; EIx – жесткость сечения участка балки. Вычисления по этой формуле производятся по участкам, на каждом из которых прямолинейная эпюра должна быть без переломов. Величина (Af*yc) считается положительной, если обе эпюры располагаются по одну сторону от балки, отрицательной, если они располагаются по разные стороны. Положительный результат перемножения эпюр означает, что направление перемещения совпадает с направлением единичной силы (или момента). Сложная эпюра Мf должна быть разбита на простые фигуры(применяется так называемое «расслоение эпюры»), для каждой из которых легко определить ординату центра тяжести. При этом площадь каждой фигуры умножается на ординату под ее центром тяжести.
iSopromat.ru
Изгибом называется вид деформации бруса, при котором в его поперечных сечениях, под действием внешних нагрузок возникают внутренние изгибающие моменты.
Деформация изгиба проявляется в искривлении продольной оси бруса.
Брус с прямой осью, подвергающийся изгибу, обычно называется балкой.
Если в сечениях балки возникает только изгибающий момент (поперечные силы отсутствуют), то изгиб называется чистым.
При изгибе одни слои балки растягиваются, а противоположные им – сжимаются, например:
Из балки нагруженной только изгибающим моментом 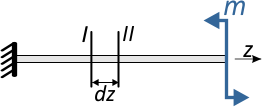
сечениями I и II мысленно вырежем фрагмент длиной dz
Как видно в данном случае верхние слои балки сжаты, а нижние – растянуты. 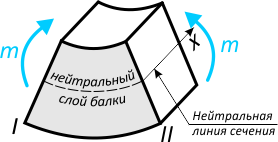
При этом наибольшему растяжению/сжатию подвержены крайние нижний и верхний слои балки.
Между ними расположен нейтральный слой, длина которого вследствие изгиба балки не изменяется.
Нейтральный слой расположен на уровне центров тяжести поперечных сечений балки, нормально к плоскости, в которой действуют изгибающие нагрузки.
Линия, образованная пересечением нейтрального слоя с поперечным сечением балки называется нейтральной линией сечения.
В общем случае плоского прямого изгиба в поперечных сечениях балки возникают два внутренних силовых фактора: изгибающий момент M и поперечная сила Q. Такой изгиб называется поперечным.
Для конкретизации направления внутренних усилий им присваиваются соответствующие индексы:
Плоский прямой (поперечный) изгиб возникает при действии на балку системы внешних сил, перпендикулярных к ее оси и лежащих в плоскости, проходящей через главную центральную ось сечения балки.
Изогнутая ось балки в этом случае – плоская кривая, совпадающая с плоскостью действия внешних сил.
Для определения внутренних силовых факторов Q и M используется метод сечений, суть которого применительно к балке показана на следующем рисунке: 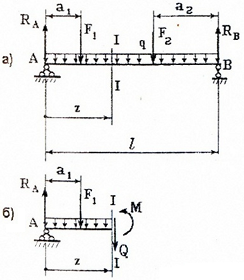
Рассматривая равновесие левой от сечения (I-I) части
с учетом правила знаков для Q и M, запишем следующие уравнения равновесия: 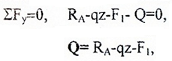
или в общем виде: 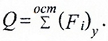
Внутренняя сила Q в поперечном сечении балки численно равна алгебраической сумме проекций на плоскость сечения всех внешних сил (активных и реактивных), действующих по одну сторону от рассматриваемого сечения. 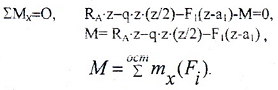
Изгибающий момент в поперечном сечении численно равен алгебраической сумме моментов внешних сил и пар, вычисленных относительно нейтральной оси рассматриваемого сечения и действующих по одну сторону от проведенного сечения.
Между изгибающим моментом M, поперечной силой Q и интенсивностью распределенной нагрузки q существуют следующие дифференциальные зависимости: 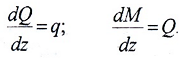
Эти формулы могут быть использованы при построении и проверке эпюр Q и M.
Графические изображения функций Q и M по длине балки называют эпюрами поперечных сил и изгибающих моментов.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Тема 2.5. Изгиб
Изгибом называется вид нагружения бруса, при котором к нему прикладывается поперечная нагрузка, лежащая в плоскости проходящей через продольную ось (рис.1). Брус, работающий при изгибе, называется балкой.
Изгиб называется плоским или прямым, если плоскость действия нагрузки проходит через главную центральную ось инерции сечения (рис.1).
Рис.1. Прямой изгиб
Если изгибающий момент Mx является единственным внутренним силовым фактором, то такой изгиб называется чистым (рис.2). При наличии поперечной силы Qy изгиб называется поперечным. Строго говоря, к простым видам сопротивления относится лишь чистый изгиб; поперечный изгиб относят к простым видам сопротивления условно, так как в большинстве случаев (для достаточно длинных балок) действием поперечной силы при расчетах на прочность можно пренебречь.
Далее будем рассматривать плоский изгиб, то есть все силы будем прилагать в плоскости симметрии балки.
Рис.2. Чистый изгиб
Осваивать расчет балок и рам удобно, рассматривая по очереди следующие вопросы:
— Определение внутренних усилий в балках и построение эпюр внутренних усилий.
— Проверка прочности балок.
— Определение перемещений и проверка жесткости балок.
§2.Построение эпюр поперечной силы и изгибающего момента
Для того, чтобы произвести расчет балки на изгиб, необходимо знать величину наибольшего изгибающего момента М и положение сечения, в котором он возникает. Точно также, надо знать и наибольшую поперечную силу Q. Для этой цели строят эпюры изгибающих моментов и поперечных сил. По эпюрам легко судить о том, где будет максимальное значение момента или поперечной силы.
Эпюра внутренней силы – график, показывающий изменение этой силы по длине балки.
Для построения эпюр балка разбивается на участки, в пределах которых функция внутренней силы не меняет своего аналитического выражения. За границы участков принимаются сечения, в которых приложены внешние нагрузки: сосредоточенные силы, сосредоточенные моменты, начинается или заканчивается распределенная нагрузка одного направления и изменяющаяся по одному закону, а также начало и конец балки.
Последовательно на каждом участке вводится скользящая система координатных осей (начало координат совмещается с началом участка) и для произвольного сечения составляются выражения для определения поперечной силы и изгибающего момента. Затем по этим выражениям в пределах каждого участка строятся графики (эпюры) внутренних сил.
Перед тем, как определять внутренние усилия (поперечные силы и изгибающие моменты) и строить эпюры, как правило, надо найти опорные реакции, возникающие в закреплении стержня. Если опорные реакции и внутренние усилия можно найти из уравнений статики, то конструкция называется статически определимой. Чаще всего мы встречаемся с тремя видами опорных закреплений стержней: жестким защемлением (заделкой), шарнирно-неподвижной опорой и шарнирно-подвижной опорой. На рис. 3 показаны эти закрепления. Для неподвижной (рис 3,б) и подвижной (рис. 3,в) опор приведены два эквивалентных обозначения этих закреплений. Напомним, что при действии нагрузки в одной плоскости в заделке возникают три опорных реакции (вертикальная, горизонтальная реакции и сосредоточенный реактивный момент) (рис. 6.5,а); в шарнирно-неподвижной опоре – две реактивные силы (рис. 3,б); в шарнирно-подвижной опоре – одна реакция – сила, перпендикулярная плоскости опирания (рис.3,в).
Рис.3. Опорные реакции: а – в заделке; б – в шарнирно-неподвижной опоре;
в – в шарнирно-подвижной опоре.
После определения опорных реакций внутренние усилия в статически определимых конструкциях определяем с помощью метода сечений.
Как было сказано выше, при плоском поперечном изгибе в балке возникают два внутренних усилия: поперечная сила Q и изгибающий момент M. В соответствии с методом сечений поперечную силу можно найти как сумму проекций всех внешних сил, взятых с одной стороны от сечения, на ось, перпендикулярную оси стержня (ось z). Изгибающий момент равен сумме моментов всех внешних сил, взятых с одной стороны от сечения, относительно оси, проходящей через центр тяжести рассматриваемого сечения (оси y).
Для того чтобы можно было вести расчет с любого конца балки, необходимо принять правило знаков для внутренних силовых факторов.
Если внешняя сила вращает отрезанную часть балки по часовой стрелке, то сила является положительной, если внешняя сила вращает отрезанную часть балки против хода часовой стрелки, то сила является отрицательной.
Если под действием внешней силы изогнутая ось балки принимает вид вогнутой чаши, такой, что идущий сверху дождь будет наполнять ее водой, то изгибающий момент является положительным. Если под действием внешней силы изогнутая ось балки принимает вид выпуклой чаши, такой, что идущий сверху дождь не будет наполнять ее водой, то изгибающий момент является отрицательным.
Поперечная сила Q в каком-либо поперечном сечении балки численно равная алгебраической сумме на ось у внешних сил действующих на балку по одну сторону от рассматриваемого сечения, а изгибающий момент M равен алгебраической сумме моментов сил, относительно центра тяжести сечения.
Взаимосвязь между нагрузкой и очертаниями эпюр поперечных сил Q и изгибающих моментов M:
Указанные закономерности позволяют упростить построения эпюр поперечных сил и изгибающих моментов (в сложнoзагруженных балках) и обойтись без составления уравнений для каждого участка.
Для определения максимальных значений изгибающих моментов дополнительно подсчитываются моменты в сечениях, где поперечные силы равны нулю. Построение без составления эпюр уравнений дает особенно значительный эффект для балок, нагруженных сложной нагрузкой, имеющих много участков нагружения.
Техническая механика
Сопротивление материалов
Изгиб
Основные понятия об изгибе
Деформация изгиба характеризуется потерей прямолинейности или первоначальной формы линией балки (ее осью) при приложении внешней нагрузки. При этом, в отличие от деформации сдвига, линия балки изменяет свою форму плавно.

На изгиб могут работать многие элементы конструкций – оси, валы, балки, зубья зубчатых колес, рычаги, тяги и т. д.
Чистый и поперечный изгиб балки
Чистым изгибом называется такой вид деформации, при котором в любом поперечном сечении бруса возникает только изгибающий момент (рис. 2).
Деформация чистого изгиба будет, например, иметь место, если к прямому брусу в плоскости, проходящей через ось, приложить две равные по величине и противоположные по знаку пары сил. Тогда в каждом сечении бруса будут действовать только изгибающие моменты.
При изучении деформации изгиба будем мысленно представлять себе, что балка (брус) состоит из бесчисленного количества продольных, параллельных оси волокон.
Чтобы наглядно представить деформацию прямого изгиба, проведем опыт с резиновым брусом, на котором нанесена сетка продольных и поперечных линий.

— поперечные линии останутся при деформации прямыми, но повернутся под углом друг другу;
— сечения бруса расширятся в поперечном направлении на вогнутой стороне и сузятся на выпуклой стороне;
— продольные прямые линии искривятся.
Из этого опыта можно сделать вывод, что:
— при чистом изгибе справедлива гипотеза плоских сечений;
— волокна, лежащие на выпуклой стороне растягиваются, на вогнутой стороне – сжимаются, а на границе между ними лежит нейтральный слой волокон, которые только искривляются, не изменяя своей длины.
Изгибающий момент и поперечная сила
Как известно из теоретической механики, опорные реакции балок определяют, составляя и решая уравнения равновесия статики для всей балки. При решении задач сопротивления материалов, и определении внутренних силовых факторов в брусьях, мы учитывали реакции связей наравне с внешними нагрузками, действующими на брусья.
Для определения внутренних силовых факторов применим метод сечений, причем изображать балку будем только одной линией – осью, к которой приложены активные и реактивные силы (нагрузки и реакции связей).
Рассмотрим два случая:
Изгибающий момент есть результирующий момент относительно нейтральной оси внутренних нормальных сил, действующих в поперечном сечении балки.
Обратим внимание на то, что изгибающий момент имеет разное направление для левой и правой частей балки. Это говорит о непригодности правила знаков статики при определении знака изгибающего момента.
Поперечная сила есть равнодействующая внутренних касательных сил в поперечном сечении балки.
Обратим внимание на то, что поперечная сила имеет противоположное направление для левой и правой частей балки, что говорит о непригодности правила знаков статики при определении знака поперечной силы.
Так как правила знаков статики неприемлемы для установления знаков изгибающего момента и поперечной силы, установим для них другие правила знаков, а именно: Если внешняя нагрузка стремится изогнуть балку выпуклостью вниз, то изгибающий момент в сечении считается положительным, и наоборот, если внешняя нагрузка стремится изогнуть балку выпуклостью вверх, то изгибающий момент в сечении считается отрицательным (рис 4,a).
Если сумма внешних сил, лежащих по левую сторону от сечения, дает равнодействующую, направленную вверх, то поперечная сила в сечении считается положительной, если равнодействующая направлена вниз, то поперечная сила в сечении считается отрицательной; для части балки, расположенной справа от сечения, знаки поперечной силы будут противоположными (рис. 4,b). Пользуясь этими правилами, следует мысленно представлять себе сечение балки жестко защемлённым, а связи отброшенными и замененными реакциями.
Что такое изгиб сопромат
Изгиб — это такой вид деформации, при котором в поперечных сечениях, нагруженных элементов конструкций, обязательно возникает изгибающий момент, а также, чаще всего, вдобавок поперечная сила. На изгиб работает множество деталей инженерных сооружений. Например, элементы металлоконструкций, используемые для возведения зданий, железобетонные плиты перекрытия, детали подъемно-транспортных машин и т.д.
Автор: Константин Вавилов · Published 21.01.2017 · Last modified 07.02.2018
Как подобрать двутавр: формулы и пример
Доброго времени суток друзья, в этой статье буду писать о том, как подобрать двутавровое поперечное сечение при плоском изгибе. Поперечное сечение при плоском изгибе, всегда подбирается по нормальным напряжениям, так как касательные напряжения при.
Автор: Константин Вавилов · Published 23.10.2015 · Last modified 15.05.2018
Расчет прогиба балки методом начальных параметров
В этой статье будут рассмотрены основные нюансы расчета прогибов, методом начальных параметров, на примере консольной балки, работающей на изгиб. А также рассмотрим пример, где с помощью универсального уравнения, определим прогиб балки и угол поворота. Теория по.
Автор: Константин Вавилов · Published 15.08.2015 · Last modified 03.12.2017
Рассмотрим технику построения эпюр изгибающих моментов и поперечных сил от распределенной нагрузки. Возьмем балку на двух опорах загруженную по всей длине распределенной нагрузкой, скажем, интенсивностью равной 3 кН/м. Длина балки один метр. Расчет эпюр.
Автор: Константин Вавилов · Published 15.08.2015 · Last modified 03.12.2017
В одном из уроков я писал про то как построить эпюру моментов используя метод сечений. Теперь предлагаю построить те же самые эпюры изгибающих моментов только быстрее. С помощью этого способа можно проверить себя, иногда сэкономить время.
Автор: Константин Вавилов · Published 15.08.2015 · Last modified 16.05.2018
Построение эпюр изгибающих моментов и поперечных сил для балок
Очень важно уметь строить эпюры для балок, работающих на изгиб! Так как построение эпюр, является неотъемлемой частью любого прочностного расчёта и большинство элементов, из которых состоят современные инженерные сооружения, работают на изгиб. Поэтому в сопромате, очень.
Автор: Константин Вавилов · Published 15.08.2015 · Last modified 03.12.2017
В этой статье я расскажу как рассчитывать детали на прочность, работающие на изгиб. Расчет на прочность при изгибе производится по нормальным и касательным напряжениям. Но в виду того, что зачастую касательные напряжения в несколько.
Автор: Константин Вавилов · Published 12.08.2015 · Last modified 03.12.2017
В этой статье будем говорить как определяется поперечная сила и изгибающий момент. Оба эти внутренних силовых фактора появляются при поперечном изгибе. При чистом изгибе, когда на конструкцию действует только моменты, в поперечных сечениях появляются.
Автор: Константин Вавилов · Published 11.08.2015 · Last modified 03.12.2017
Статически неопределимая рама. Задача №12
Известна рама, закрепленная посредством двух шарнирно подвижных опор и жесткой заделки.На раму действует один момент, одна сила и распределенная нагрузка на расстоянии 1,2 метра.Раскрыть статическую неопределимость, построить окончательные эпюры. Произвести проверки правильности решения: статическую.