что такое истинный размер

21. Основные понятия и определения по допускам и посадкам. Допуски, посадки и технические измерения.

21. Основные понятия и определения по допускам и посадкам. Допуски, посадки и технические измерения. 21. Основные понятия и определения по допускам и посадкам. Допуски, посадки и технические измерения.

Поверхности, размеры, отклонения и допуски. Поверхности деталей бывают сопрягаемыми и несопрягаемыми, или свободными. При этом они могут быть цилиндрическими, плоскими, коническими, эвольвентными, сложными (шлицевые, винтовые) и др. Со-прягаемыми называют поверхности, по которым детали соединяются в сборочные единицы, а сборочные единицы — в механизмы. Несопрягаемыми, или свободными, — конструктивно необходимые поверхности, не предназначенные для соединения с поверхностями других деталей.

Внутренние цилиндрические поверхности, а также внутренние поверхности с парал-лельными плоскостями (отверстия в ступицах, шпоночные пазы и пр.) являются охватывающими (их условно называют отверстиями; диаметры отверстий обозначают буквой D). Наружные отверстия (цилиндрическая поверхность вала, боковые грани шпонок) являются охватываемыми (их условно называют валами и обозначают буквой d).

Размеры — это числовое значение линейной величины (диаметра, длины и т.д.), они делятся на номинальные, действительные и предельные. В машино и приборостроении все размеры в технической документации задают и указывают в миллиметрах.

Номинальный размер (D) — размер, относительно которого определяют предельные размеры и отсчитывают отклонения. Номинальные размеры являются основными размерами деталей или их соединений. Сопрягаемые поверхности имеют общий номинальный размер.

Действительный размер (Dr, dr) — размер, установленный измерением с допустимой погрешностью. Погрешностью измерения называется отклонение результата измерения от истинного значения измеряемой величины. Погрешность измерения, а следовательно, и выбор измерительных средств необходимо согласовывать с точностью, которая требуется для данного размера.

Предельные размеры — два предельно допустимых размера, между которыми должен находиться или которым может быть равен действи¬тельный размер. Больший из двух предельных размеров называют наибольшим предельным размером (Dmax, dmax), а меньший — наименьшим предельным размером (Dmin, dmin) Предельные размеры позво¬ляют оценивать точность обработки деталей.

Отклонение — это алгебраическая разность между действительным и соответствующим номинальными размерами. Отклонения отверстий обозначают буквой E, валов — e.

Действительное отклонение (Er, er) равно алгебраической разности действительного и номинального размеров: Er = Dr — D; er = dr — d.

Предельное отклонение равно алгебраической разности предельного и номинального размеров. Различают верхнее, нижнее и среднее отклонения. Верхнее (ES, es) равно алгебраической разности наибольшего предельного и номинального размеров: ES = Dmax — D; es = dmax — D.

Нижнее отклонение (EI, ei) равно алгебраической разности наименьшего предельного и номинального размеров: EI = Dmin — D; ei = Dmin — D.
Среднее отклонение (Em, em) равно полусумме верхнего и ниж¬него отклонений: Em = 0,5 (ES + EI), em = 0,5 (es + ei).
Пример. Определить предельные и средние отклонения для штифтов, у которых D = 20 мм, dmax = 20,01 мм и dmin = 19,989 мм.

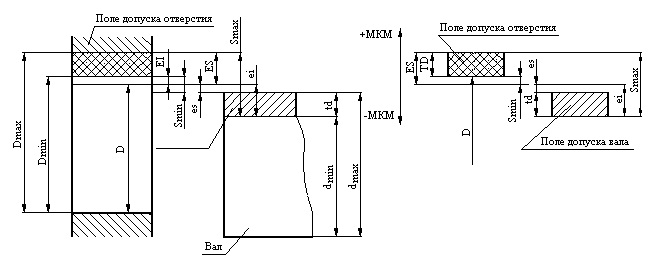
Для графического построения полей допусков и посадок проводят горизонтальную линию 00, называемую нулевой. Нулевая — это линия, положение которой соответствует номинальному размеру и от которой откладываются предельные отклонения размеров. По-ложительные отклонения — вверх от нулевой линии, отрицательные — вниз.

Поле допуска — поле, ограниченное верхним и нижним отклонения¬ми. Оно опре-деляется величиной допуска и его положением относитель¬но номинального размера. При графическом изображении поля допусков показывают зоны, которые ограничены двумя ли-ниями, проведенными на расстояниях, соответствующих верхнему и нижнему отклоне¬нию.
На схемах указывают номинальный D и предельные (Dmax, Dmin, dmax, dmin) размеры, предельные отклонения (ES, EI, es, ei) поля допусков и другие параметры.

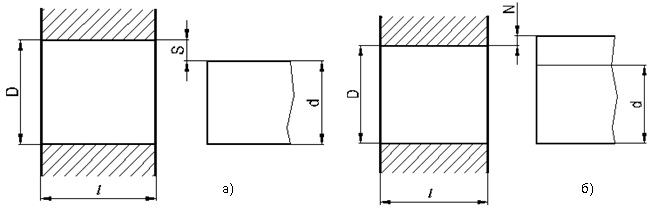
Понятия о посадках и допуске посадки. Если у соединяемых между собой деталей размер отверстия больше размера вала, то в соединении будет зазор (S). Если же размер ва-ла больше размера отверстия, то в соединении будет натяг (N). Зазором называется по-ложительная разность между размерами отверстия и вала S = D — d (рис. 42, а). а натягом — положительная разность между размером вала и отверстия N = d — D (рис. 42, б).

В машинах и приборах требуются посадки с различными зазорами и натягами. В тех случаях, когда одна деталь должна перемещаться относительно другой без качки, следует иметь очень малый зазор: для того чтобы одна деталь могла свободно вращаться в другой (например, вал в отверстии), зазор должен быть больше. Если соединенные вал и втулка представляют собой как бы одно целое, они соединены с натягом и не могут перемещаться относительно друг друга.
Посадки подразделяют на три вида: подвижные, обеспечивающие зазор в соединении: неподвижные (прессовые), обеспечивающие натяг в соединении; переходные, ко-торые наз¬ваны так потому, что до сборки вала и втулки нельзя сказать, что будет в соединении — зазор или натяг, так как заданные отклонения на вал и отверстие перекрывают друг друга.

В зависимости от использованного допуска у той и другой детали при переходной посадке может оказаться, что размер вала больше размера отверстия или размер отверстия больше размера вала.

Для оценки точности соединений (посадок) пользуются понятием допуска посадки, под которым понимается разность между наибольшим и наименьшим зазорами (в посадках с зазором) или наибольшим и наименьшим натягами (в посадках с натягом). В переходных посадках допуск посадки равен разности между наибольшим и наименьшим натягами или сумме наибольшего натяга и наибольшего зазора. Допуск посадки равен также сумме допусков отверстия и вала.

Источник

ОСНОВНЫЕ ПОНЯТИЯ О РАЗМЕРАХ, ОТКЛОНЕНИЯХ И ДОПУСКЕ

Различают действительный, номинальный и предельные размеры.

Действительный размер – размер, установленный измерением с помощью средства измерения с допускаемой погрешностью измерения.

Под погрешностью измерения понимается отклонение резуль­тата измерения от истинного значения измеряемой величины. Истинный размер – размер, полученный в результате изготов­ления и значение которого нам не известно.

Номинальный размер указывается на чертеже и является общий для отверстия и вала, об­разующих соединение и определяется на стадии разработки изделия исходя из функционального назначения деталей путем вы­полнения кинематических, динамических и прочностных расчетов с учетом конструктивных, технологических, эстетических и других условий.

Стандарт на нормальные линейные размеры имеет большое экономическое значение, состоящее в том, что при сокращении числа номинальных размеров сокращается потребная номенклату­ра мерных режущих и измерительных инструментов (сверла, зен­керы, развертки, протяжки, калибры), штампов, приспособле­ний и другой технологической оснастки. При этом создаются усло­вия для организации централизованного изготовления названных инструментов и оснастки на специализированных машинострои­тельных заводах.

Стандарт не распространяется на технологические межопера­ционные размеры и на размеры, связанные расчетными зависи­мостями с другими принятыми размерами или размерами стан­дартных комплектующих изделий.

Предельные размеры — два предельно допустимых размера, меж­ду которыми должен находиться или которым может быть равен действительный размер.

Сравнивая действительный размер с предельными, можно судить о годности элемента детали. Условиями годности являются соотношения: для отверстий D_min

Особенность отклонений заключается в том, что они всегда име­ют знак (+) или (-). В частном случае одно из отклонений может быть равно нулю, т.е. один из предельных размеров может совпадать с номинальным зна­чением.

Допуском размера называется разность между наибольшим и наименьшим предельными размерами или алгебраическая разность между верхним и нижним отклонениями.

Согласно определению: допуск отверстия T_D=D_max-D_min; допуск вала Td=d_max-d_min. Допуск размера всегда положительная величина.

Допуск раз­мера выражает разброс действительных размеров в пределах от наибольшего до наименьшего предельных размеров, физически определяет величину официально разрешенной погрешности дей­ствительного размера элемента детали в процессе его изготовле­ния.

Для графического изображения полей допусков, позволяющего понять соотношения номинального и предельных размеров, пре­дельных отклонений и допуска, введено понятие нулевой линии.

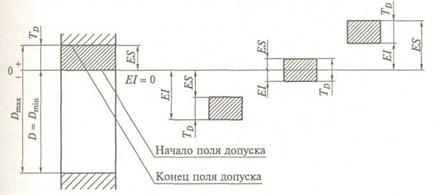Рис. 1.4. Схема расположения полей допусков отверстий

Поля допусков отверстий и валов могут занимать различное расположение относительно нулевой линии, что необходимо для образования различных посадок.

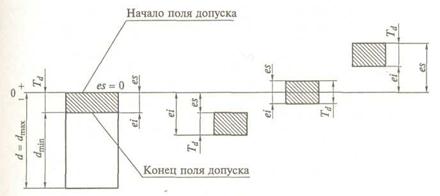Рис. 1.5. Схема расположения полей допусков валов

Чем меньше допуск, тем точнее будет изготовлен элемент детали. Чем больше допуск, тем грубее элемент детали. Но в то же время, чем меньше допуск, тем труднее, сложнее и отсюда дороже изготовление элемента деталей; чем допуски больше, тем проще и дешевле изготовить элемент детали.

Источник

Понятие о размере. Размеры номинальный, действительный, истинный, нормальный. Ряды нормальных линейных размеров

Размер – числовое значение линейной величины (диаметра, длины и т. п.) в выбранных единицах измерения.

Размер номинальный – это размер, относительно которого определяются отклонения.

Номинальный размер определяется конструктором в результате расчётов габаритных размеров или на прочность, или на жёсткость, или с учётом конструктивных и технологических соображений. Но т. к. экономическая эффективность взаимозаменяемости заключается в ограничении номенклатуры различных изделий, а также в ограничении номенклатуры размеров каждого изделия, конструктор не может принять любой расчётный размер за номинальный. Поэтому расчётный размер округляется до ближайшего нормального размера (большего или меньшего чем расчётный в зависимости от требований, определяющих расчётный размер) из ряда предпочтительных чисел.

Размер действительный – размер элементов детали, установленный измерением, с допускаемой погрешностью.

Размер истинный – это размер, полученный в результате изготовления и значение его нам не известно, хотя он и существует.

Этот размер близок к действительному размеру. Поэтому понятие «истинный размер» часто заменяют понятием «действительный размер».

Размер нормальный – это размер выбранный из ряда предпочтительных чисел, представляющих собой геометрическую прогрессию.

Ряды предпочтительных чисел, т.е. значения, до которых должны округляться расчётные значения, имеют ограниченный набор чисел и во всём мире приняты одинаковые, т.к. от этого зависит экономическая эффективность взаимозаменяемости. Это даёт возможность сократить количество типоразмеров деталей и узлов, количество режущего инструмента и другой технологической и измерительной оснастки.

(Геометрическая прогрессия – это ряд чисел, в котором каждое последующее число получается умножением предыдущего на одно и тоже число – знаменатель прогрессии.)

Для определения нормальных чисел приняты следующие знаменатели: 5 √10; 10 √101; 20 √10; 40 √10, которые приблизительно равны 1,6; 1,25; 1,12; 1,06.

Ряды нормальных чисел условно названы R5; R10; R20; R40.

Источник

Правила нанесения размеров

3.1. Основные положения стандарта

Основанием для определения величины изделия и его элементов служат размерные числа, нанесенные на чертеже. Размеры всегда указывают истинные независимо от того, в каком масштабе и с какой точностью выполнено изображение. Размеры должны быть назначены и нанесены так, чтобы по ним можно было изготовить деталь, не прибегая к подсчетам.

Согласно ГОСТ 2.307-2011 — «Нанесение размеров и предельных отклонений» линейные размеры на чертеже приводят в миллиметрах, без обозначения единицы измерения. Угловые размеры указывают в градусах, минутах, секундах с обозначением единицы измерения. Каждый размер наносят на чертеже, в основной надписи только один раз, повторять его недопустимо.

При указании размеров прямолинейных отрезков размерные линии проводят параллельно этим отрезкам на расстоянии не менее 10 мм от линии контура и 7 мм друг от друга, а выносные линии проводят перпендикулярно размерным. Выносные линии должны выходить за концы стрелок размерной линии на 1…5 мм. Стрелка размерной линии должна иметь длину не менее 2,5 мм и угол при вершине около 20° (Рисунок 3.1). Размеры и форма стрелок должна быть одинаковыми на всем чертеже.

3.2. Нанесение размеров

На чертежах деталей размеры проставляют, исходя из технологии изготовления данной детали и из того, какими поверхностями данная деталь соприкасается с другими деталями сборочной единицы.

Это сказывается на выборе конструкторской базы.

Базированием называется придание заготовке требуемого положения относительно выбранной системы координат.

Базой называется поверхность или сочетание поверхностей, ось или точка, принадлежащие изделию или заготовке, и используемые для базирования.

Конструкторская база — база используемая для определения положения детали или сборочной единицы в изделии.

Основное правило нанесения размеров — группирование размеров, относящихся к одному геометрическому элементу на одном изображении, на том, на котором данный элемент наиболее наглядно представлен. Не всегда это удается выполнить, но к этому всегда стремимся.

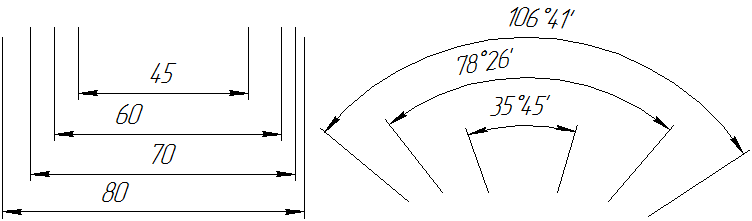
При указании размера угла размерную линию проводят в виде дуги с центром в его вершине, а выносные линии – радиально (Рисунок 3.2).

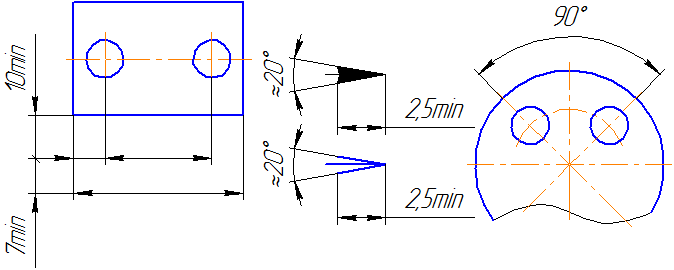Рисунок 3.1	Рисунок 3.2

Размерные линии предпочтительно наносить вне контура изображения. Не допускается использование линии контура, осевые, центровые и выносные линии в качестве размерных. Недопустимо пересечение размерных и выносных линий, показанное на зачеркнутом Рисунке 3.3, а. Правильное нанесение размеров для этого случая приведено на Рисунке 3.3, б.

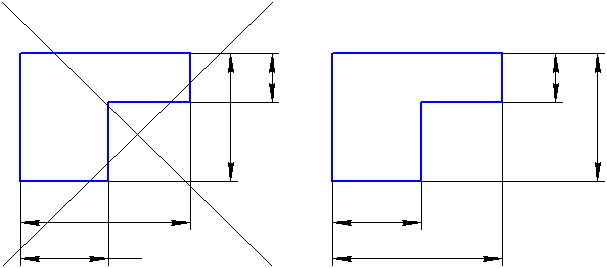а	б

Как видим, меньшие размеры следует размещать ближе к контуру детали, число пересечений размерных и выносных линий при этом сократится, что облегчит чтение чертежа.

Размерную линию проводят с обрывом, если с одной стороны изображения нет возможности провести выносную линию, например, в случае совмещения вида и разреза (Рисунок 3.4, а), а также, если вид или разрез симметричного предмета изображают только до оси или с обрывом (Рисунок 3.4, б). Обрыв размерной линии делают дальше оси или линии обрыва предмета.

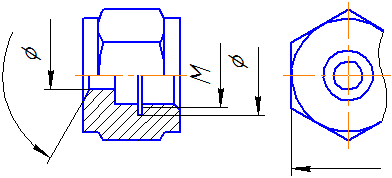а	б

Размерные линии допускается проводить с обрывом в следующих случаях:

Основная линия должна быть прервана, если она пересекается со стрелкой (Рисунок 3.5).

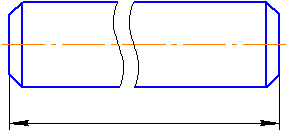
При изображении изделия с разрывом размерную линию не прерывают (Рисунок 3.7). Размерное число, при этом, должно соответствовать полной длине детали.

Рисунок 3.7

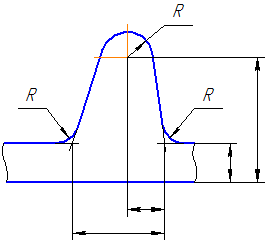
Если нет возможности разместить размерные числа и стрелки между близко расположенными сплошными основными или тонкими линиями, их наносят снаружи (Рисунок 3.8). Аналогично поступают при нанесении размера радиуса, если стрелка не помещается между кривой и центром радиуса (Рисунок 3.9).

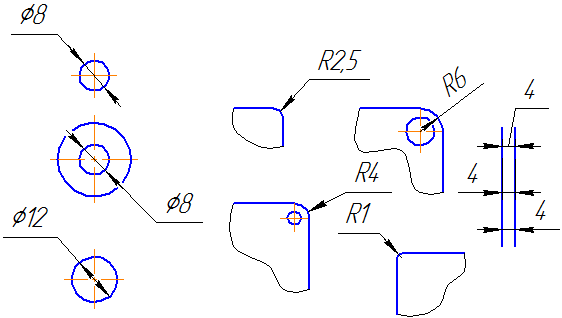Рисунок 3.8	Рисунок 3.9

Допускается заменять стрелки точками или засечками, наносимыми под углом 45° к размерным линиям, если между выносными линиями невозможно разместить стрелку (Рисунок 3.10).

Рисунок 3.10

Размерные числа не допускается разделять или пересекать какими-либо линиями чертежа. В месте нанесения размерного числа осевые, центровые линии или линии штриховки прерывают (Рисунок 3.11).

Рисунок 3.11

Рисунок 3.12

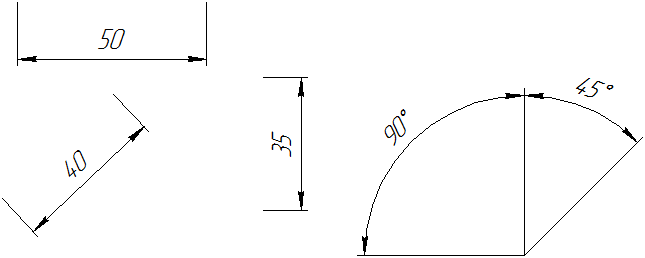
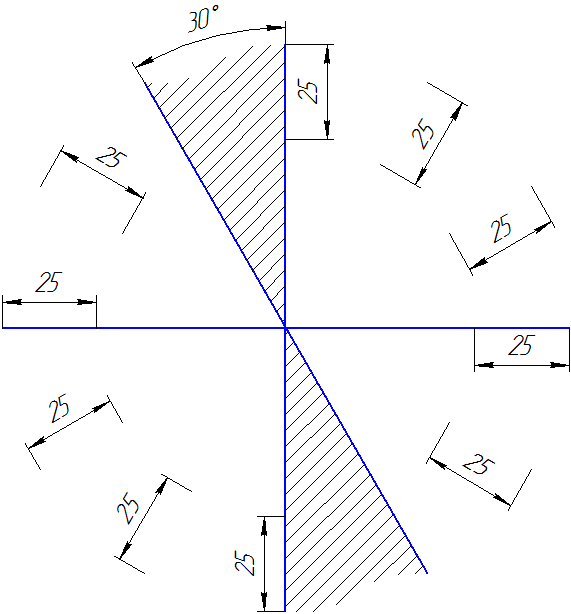
Размерные числа линейных размеров при различных наклонах размерных линий располагают, как показано на Рисунке 3.13.

Если необходимо нанести размеров заштрихованной зоне, соответствующее размерное число наносят на полке линии – выноски.

Рисунок 3.13
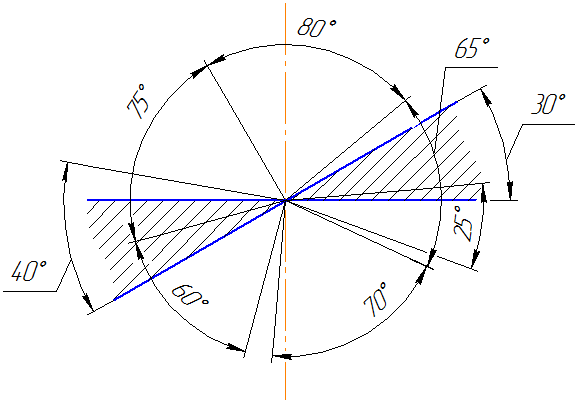
Угловые размеры наносят так, как показано на Рисунке 3.14.

Рисунок 3.14

В зоне расположенной выше горизонтальной осевой линии, размерные числа помещают над размерными линиями со стороны их выпуклости, в зоне расположенной ниже горизонтальной осевой линии – со стороны вогнутости размерной линии.

Размерные числа над параллельными размерными линиями следует располагать в шахматном порядке (Рисунок 3.15).

Рисунок 3.15

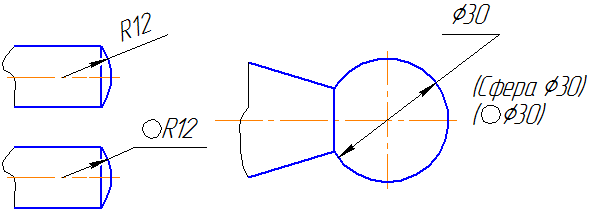
При указании размера диаметра во всех случаях перед размерным числом наносят знак Ø. Перед размерным числом диаметра (радиуса) сферы также наносят знак «Ø» (R) без надписи «Сфера» (Рисунок 3.16).

Рисунок 3.16

Если на чертеже трудно отличить сферу от других поверхностей, допускается наносить слово «Сфера» или знак «О», например, «Сфера Ø18, OR12». Диаметр знака сферы равен высоте размерных чисел на чертеже.
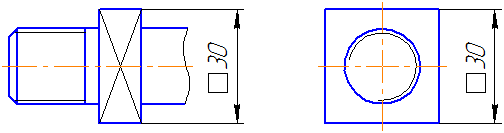
Размеры квадрата наносят, как показано на чертеже (Рисунок 3.17).

Рисунок 3.17

Высота знака должна быть равна высоте размерных чисел на чертеже.

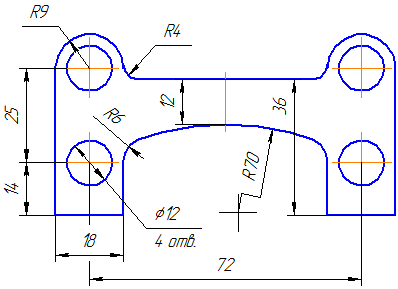
При нанесении размера радиуса перед размерным числом помещают прописную букву R. При большей величине радиуса центр допускается приближать к дуге, в этом случае размерную линию радиуса показывать с изломом под углом 90° (Рисунок 3.18). Если не требуется указывать размеры, определяющие положение центра дуги окружности, то размерную линию радиуса допускается не доводить до центра и смещать ее относительно центра (Рисунок 3.19).

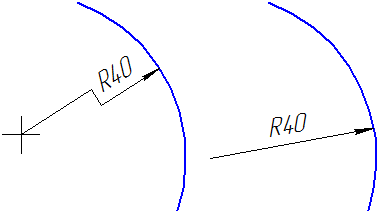Рисунок 3.18	Рисунок 3.19

Радиусы скруглений, размер которых в масштабе чертежа 1 мм и менее, на чертеже не изображают и размеры их наносят, как показано на Рисунке 3.20.
При нанесении размера дуги окружности размерную линию проводят концентрично дуге, а выносные линии – параллельно биссектрисе угла, и над размерным числом наносят знак «⌒» (Рисунок 3.21).

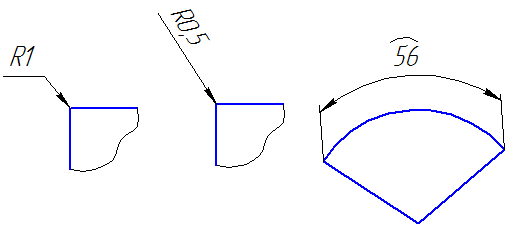Рисунок 3.20	Рисунок 3.21

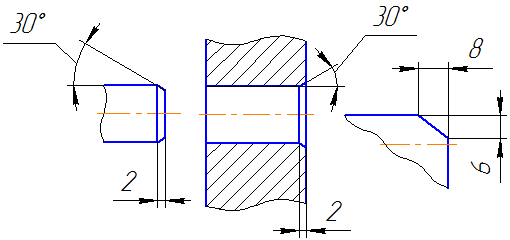
Размеры фасок, имеющих другие углы, наносят по общим правилам – двумя линейными размерами или линейным и угловым размерами (Рисунок 3.23).

Вопрос, какие размеры следует наносить на чертеже, решается с учетом технологии изготовления деталей и контроля изготовления.

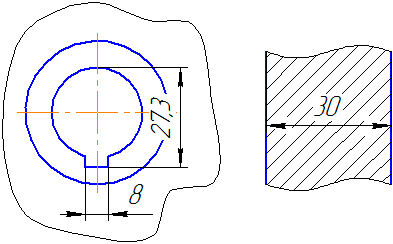
Как правило, размеры полных окружностей ставятся диаметром, неполных окружностей – радиусом.

Когда требуется задать расстояния между окружностями, например, изображающими отверстия, задают, расстояния между центрами окружностей и расстояние от центра любой окружности до одной из поверхностей детали.

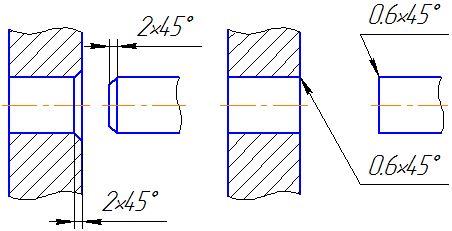а	б

Рисунок 3.22

Рисунок 3.23
Поверхности, от которых задают размеры других элементов детали, называют базовыми поверхностями или базами.
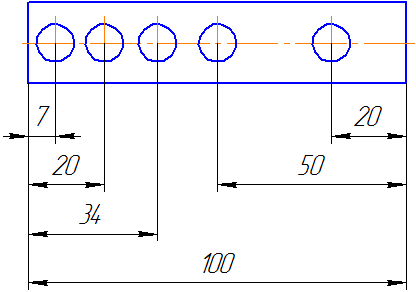
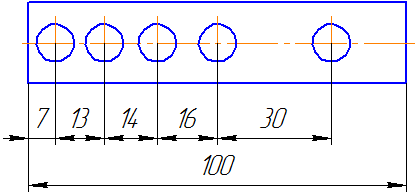
Существует несколько способов нанесения размеров:

Такая система имеет преимущество, но при этом размеры являются независимыми друг от друга, ошибка одного из них не отражается на других.

Рисунок 3.24

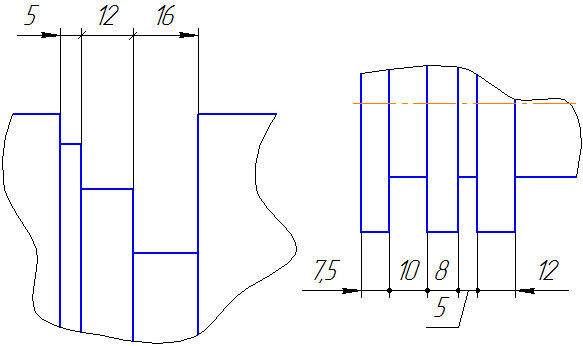
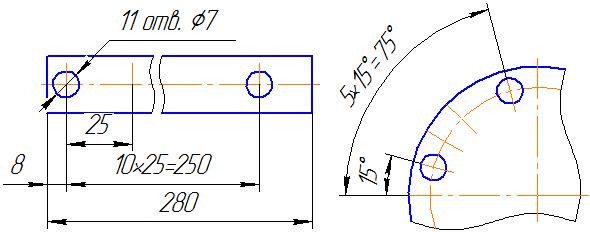
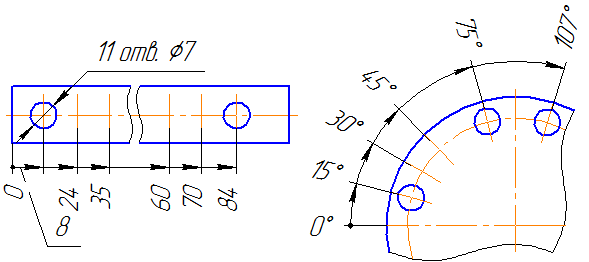
При нанесении размеров, определяющих расстояние между равномерно расположенными одинаковыми элементами изделия (например, отверстиями), рекомендуется вместо размерных цепей наносить размер между соседними элементами и размер между крайними элементами в виде произведения количества промежутков между элементами на размер промежутка (Рисунок 3.27).

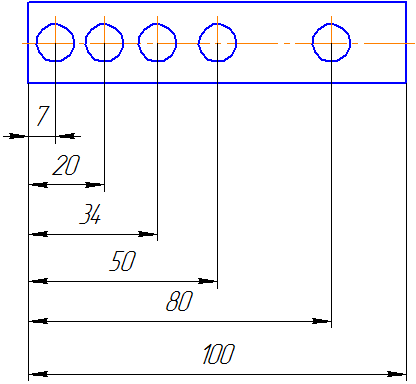
При большом количестве размеров, нанесенных от общей базы, допускается наносить линейные и угловые размеры, как показано на Рисунке 3.28, при этом проводят общую размерную линию от отметки «0» и размерные числа наносят в направлении выносных линий у их концов.

Рисунок 3.27

Рисунок 3.28

Допускается не наносить на чертеже размеры радиуса сопряжения параллельных линий (Рисунок 3.29).

Рисунок 3.29

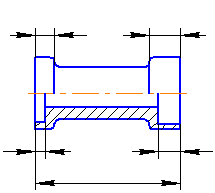
Наружные и внутренние контуры деталей при изготовлении и контроле измеряют отдельно, поэтому на чертеже их размеры следует наносить раздельно (Рисунок 3.30).

Рисунок 3.30

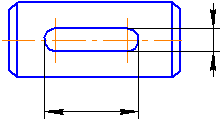
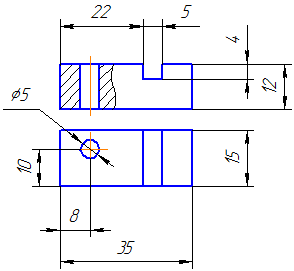
Размеры, относящиеся к одному и тому же конструктивному элементу (пазу, выступу, отверстию и т.п.), рекомендуется группировать в одном месте, располагая их на том изображении, на котором геометрическая форма данного элемента показана наиболее полно (Рисунок 3.31).

Рисунок 3.31
При наличии у детали скруглений размеры частей детали наносят без учета скруглений с указанием радиусов скруглений (Рисунок 3.32).

Рисунок 3.32

Размеры симметрично расположенных элементов изделия (кроме отверстий) наносят один раз без указания их количества, группируя, как правило, в одном месте все размеры (Рисунок 3.33).

Рисунок 3.33

Одинаковые элементы, расположенные в разных частях изделия (например, отверстия) рассматривают как один элемент, если между ними нет промежутка (Рисунок 3.34, а) или, если эти элементы соединены тонкими сплошными линиями (Рисунок 3.34, б). При отсутствии этих условий указывают полное количество элементов (Рисунок 3.34, в).

Размеры нескольких одинаковых элементов изделия, как правило, наносят один раз, с указанием на полке линии – выноски количества этих элементов (Рисунок 3.35).

Рисунок 3.35

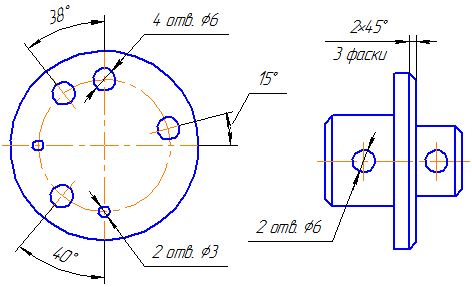
При нанесении размеров элементов, равномерно расположенных по окружности (например, отверстий), вместо угловых размеров, определяющих взаимное расположение элементов, указывают только их количество (Рисунок 3.36 — 3.38).

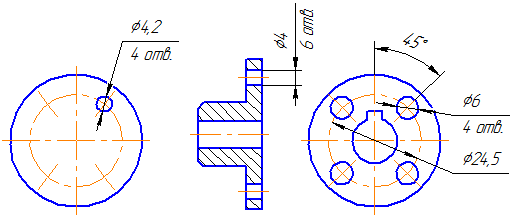Рисунок 3.36	Рисунок 3.37	Рисунок 3.38

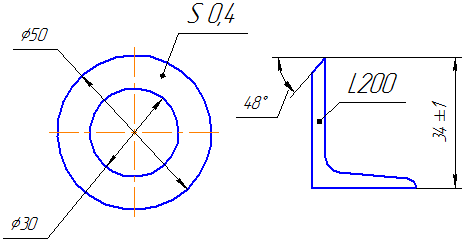
При изображении детали в одной проекции размер ее толщины или длины наносят, как показано на Рисунке 3.39.

Рисунок 3.39
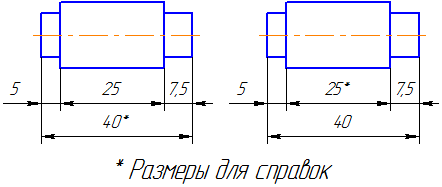
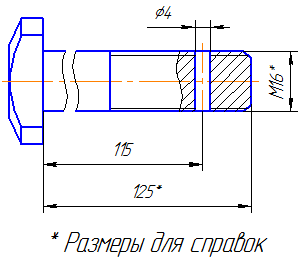
Размеры на чертеже не допускается наносить в виде замкнутой цепи, за исключением случаев, когда один из размеров указан как справочный.
Справочные размеры – размеры, не подлежащие выполнению по данному чертежу и указанные для большего удобства пользования чертежом.

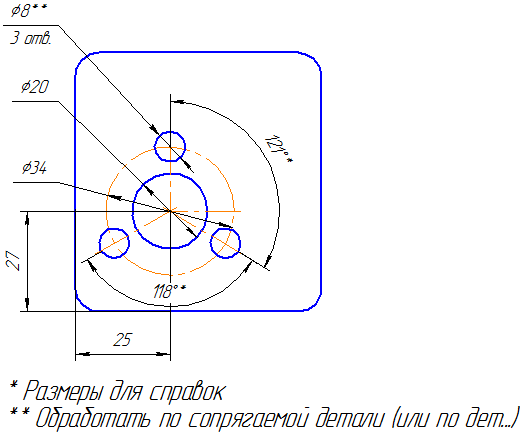
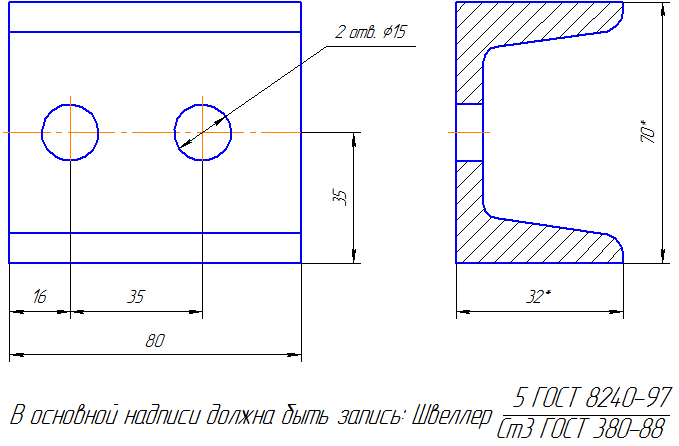
Справочные размеры на чертеже отмечают знаком «*», а в технических требованиях записывают «* Размеры для справок». Если же все размеры на чертеже справочные, их знаком «*» не отмечают, а в технических требованиях записывают «Размеры для справок».

К справочным размерам относятся следующие размеры:

Рисунок 3.40

Рисунок 3.41

Рисунок 3.42

Рисунок 3.43
Примечания:

Источник