что такое испытание в математике

Математика — онлайн помощь

Как любая наука, теория вероятностей имеет свои исходные понятия, через которые определяются другие понятия. К основным понятиям теории вероятностей относятся: испытание, событие, вероятность события.

Изучение явлений происходит путем наблюдений и опытов, проводимых при определенных условиях. Испытанием в теории вероятностей называется осуществление какого-либо комплекса условий, при котором наблюдается данное явление. Предполагается, что данный комплекс условий может быть воспроизведен сколь угодно большое число раз. Итак, в теории вероятностей вместо слов “произведено наблюдение при осуществлении определенного комплекса условий” говорят кратко “произведено испытание”.

Событием называется всякий факт, который может наступить в результате испытания.

События можно классифицировать по степени возможности их появления и по характеру взаимосвязи.

Достоверным называется событие, которое в данном испытании всегда наступает, его обозначают .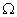

Невозможным называется событие, которое в данном испытании никогда не наступает, его обозначают .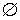

Случайным называется событие, которое в данном испытании может наступить, а может не наступить. Случайные события обозначают заглавными буквами латинского алфавита А, В, С,…

.

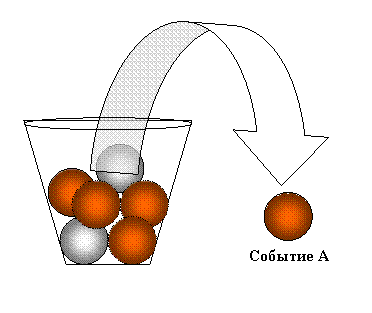
События называются несовместными, если появление одного из них исключает появление других событий в данном испытании. В противном случае события называются совместными. Примеры несовместных событий: появление герба и цифры при одном бросании монеты, попадание и промах при одном выстреле. Те же попадание и промах при двух выстрелах являются уже совместными событиями.

Несколько событий образуют полную группу событий, если в результате испытания обязательно наступит хотя бы одно из них. В частности, если события образуют полную группу и несовместны, то в результате испытания появится одно и только одно из этих событий.

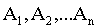
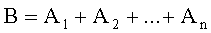
Суммой событий . называется событие, состоящее в наступлении хотя бы одного из этих событий.

.

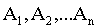
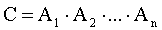
Произведением событий его обозначают . называется событие, состоящее в совместном появлении всех этих событий.

.

Уважаемые студенты
На нашем сайте можно получить помощь по всем разделам математики и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Основные понятия теории вероятностей

Что нужно знать

Это самая первая, вводная статья по теории вероятностей. Сама наука является достаточно самостоятельным разделом математики, и, чтобы понять её основы (а также для того, чтобы научиться решать простейшие задачи вроде задания 4 из ЕГЭ), нужно лишь уметь совершать арифметические действия с числами и дробями. Так что, если вам тяжело даются логарифмы и тригонометрия или совершенно непонятна производная, это никак не помешает вам разобраться в теории вероятностей.

Что вы узнаете

Что такое испытание и исход

Испытанием в теории вероятностей называют какой-нибудь эксперимент (не обязательно научный). Например, подбросили монетку — испытание. Вытянули лотерейный билет — испытание. Провели жеребьёвку спортивного соревнования — тоже испытание. Вообще говоря, эксперимент должен быть повторяемым. То есть, чтобы мы могли говорить о вероятности, у нас должна быть возможность провести эксперимент не один (а если совсем строго, то сколько угодно) раз.

Если есть эксперимент, есть и возможные результаты — то, чем он может закончиться. Список возможных результатов можно составлять по-разному, но стандартный способ — выбрать максимальное дробление результатов. Например, при бросании кубика можно сказать, что есть два результата: <выпало 6 6 6 > и <выпало не 6 6 6 >, — но это не очень удобно, так как второй результат можно раздробить на более мелкие. Составляя список возможных результатов, мы должны также помнить, что два результата никогда не могут случиться одновременно (условие взаимоисключения).

На столе лежит колода карт, а мы вытягиваем оттуда одну карту. Это пример случайного испытания. У этого испытания 5 2 52 5 2 исхода, так как мы можем вытянуть любую из 5 2 52 5 2 карт (в каждой из четырех мастей 1 3 13 1 3 карт от двойки до туза).

Бросок обыкновенного игрального кубика является классическим примером испытания. Сколько исходов возможно у этого испытания?

Важно понимать, что список возможных результатов мы очерчиваем сами (исходя из «здравого смысла»). Так, при броске монеты мы считаем «возможным», что она упадёт вверх аверсом («орлом») или вверх реверсом («решкой»), просто не рассматривая возможности того, что монета встанет на ребро, будет проглочена пролетающей птицей и т.п. В то же время мы считаем несущественным, упадёт монета на стол или на пол, со звоном или бесшумно и пр.; мы ограничили себя двумя интересующими нас исходами.

Рассмотрим чуть более сложный пример: мы одновременно подкинули монету и бросили игральный кубик. Сколько (и каких) исходов у этого испытания?

Для ответа на этот вопрос попробуем составить список результатов. Для монеты: Орёл (О) и Решка (Р). Для кубика: 1, 2, 3, 4, 5, 6. А теперь посмотрим, что может быть с кубиком, если монета выпала на Орла? Но ведь кубику в некотором смысле «всё равно», как выпала монета (в теории вероятностей это называется «независимые события», но об этом позже). То есть для него по-прежнему возможны все 6 вариантов. То же самое и если она выпала на Решку. Значит, можно перечислить все возможные исходы подряд, в виде «результат монеты» — «результат кубика». Сделаем это:

Представим следующее испытание: два игральных кубика бросают одновременно. Сколько исходов будет в этом случае?

Что такое случайное событие

Случайное событие — это подмножество множества исходов испытания.

Из скольки исходов состоит случайное событие «выпал дубль» (то есть одинаковые числа на кубиках) при испытании «бросание двух кубиков одновременно»?

Попробуйте ответить на вопрос посложнее:

Из скольки исходов состоит случайное событие «сумма очков на двух кубиках меньше 4»? Испытание то же — два кубика бросают одновременно.

Как считать вероятность события

Исходы, входящие в событие, называются благоприятными для этого события.

Прежде чем перейти к классическому определению вероятности, заметим, что для его применения требуется выполнение определённого условия — равновозможности всех исходов. Это условие может быть недостаточно строго определено, но интуитивно оно понятно. Например, если в качестве исходов при бросании монеты выбрать «орёл», «решка» и «ребро», то классическое определение вероятности применять нельзя, так как шансы на последний исход меньше, чем на первые два. А если выбрать только «орёл» и «решка», то можно — ведь нет никаких оснований считать один исход более частым, чем другой.

Итак, пусть у нас есть испытание с определённым набором равновозможных исходов. Вероятностью некоторого случайного события называется отношение количества благоприятных исходов к общему количеству исходов испытания.
P < Событие A >= Число исходов, благоприятных для A Общее число исходов P\<\text<Событие >A\>=\frac <\text<Число исходов, благоприятных для >A><\text<Общее число исходов>> P < Событие A >= Общее число исходов Число исходов, благоприятных для A ​

Конечно, «в жизни» в основном встречаются ситуации, когда одни исходы встречаются чаще других, и тогда нужно использовать скорректированное определение вероятности. Но в школьных задачах исходы всегда одинаково ожидаемы, так что для нахождения вероятности нужно только правильно посчитать количество исходов, входящих в событие, и общее количество исходов испытания, после чего поделить одно на другое.

Рассмотрим пример. Из стандартной колоды карт (от двойки до туза) наугад вытащили одну карту. Какова вероятность, что эта карта — с цифрой?

Чему равна вероятность достоверного события?

Попробуйте решить несложную задачу, чтобы убедиться, что всё понятно.

В классе 21 человек, среди них 2 Саши. Классный руководитель назначил дежурной Настю и случайным образом выбирает ей напарника. Какова вероятность, что напарником окажется Саша? (Запишите ответ в виде десятичной дроби.)

Эту статью написал для вас Сергей Вальковский, учитель математики Центра образования «Пятьдесят седьмая школа», Москва.

Источник

Теория вероятностей, формулы и примеры

Тема непростая, но если вы собираетесь поступать на факультет, где нужны базовые знания высшей математики, освоить материал — must have. Тем более, все формулы по теории вероятности пригодятся не только в универе, но и при решении 4 задания на ЕГЭ. Начнем!

Основные понятия

Французские математики Блез Паскаль и Пьер Ферма анализировали азартные игры и исследовали прогнозы выигрыша. Тогда они заметили первые закономерности случайных событий на примере бросания костей и сформулировали теорию вероятностей.

Когда мы кидаем монетку, то не можем точно сказать, что выпадет: орел или решка.

Но если подкидывать монету много раз — окажется, что каждая сторона выпадает примерно равное количество раз. Из чего можно сформулировать вероятность: 50% на 50%, что выпадет «орел» или «решка».

Теория вероятностей — это раздел математики, который изучает закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.

Вероятность — это степень возможности, что какое-то событие произойдет. Если у нас больше оснований полагать, что что-то скорее произойдет, чем нет — такое событие называют вероятным.

Ну, скажем, смотрим на тучи и понимаем, что дождь — вполне себе вероятное событие. А если светит яркое солнце, то дождь — маловероятное или невероятное событие.

Случайная величина — это величина, которая в результате испытания может принять то или иное значение, причем неизвестно заранее, какое именно. Случайные величины можно разделить на две категории:

Вероятностное пространство — это математическая модель случайного эксперимента (опыта). Вероятностное пространство содержит в себе всю информацию о свойствах случайного эксперимента, которая нужна, чтобы проанализировать его через теорию вероятностей.

Формулы по теории вероятности

Теория вероятности изучает события и их вероятности. Если событие сложное, то его можно разбить на простые составные части — так легче и быстрее найти их вероятности. Рассмотрим основные формулы теории вероятности.

Случайные события. Основные формулы комбинаторики

Классическое определение вероятности

Вероятностью события A в некотором испытании называют отношение:

P (A) = m/n, где n — общее число всех равновозможных, элементарных исходов этого испытания, а m — количество элементарных исходов, благоприятствующих событию A

Таким образом, вероятность любого события удовлетворяет двойному неравенству:

Пример 1. В пакете 15 конфет: 5 с молочным шоколадом и 10 — с горьким. Какова вероятность вынуть из пакета конфету с белым шоколадом?

Так как в пакете нет конфет с белым шоколадом, то m = 0, n = 15. Следовательно, искомая вероятность равна нулю:

Неприятная новость для любителей белого шоколада: в этом примере событие «вынуть конфету с белым шоколадом» — невозможное.

Пример 2. Из колоды в 36 карт вынули одну карту. Какова вероятность появления карты червовой масти?

Количество элементарных исходов, то есть количество карт равно 36 (n). Число случаев, благоприятствующих появлению карты червовой масти (А) равно 9 (m).

Геометрическое определение вероятности

Геометрическая вероятность события А определяется отношением:

P(A)= m(A)/m(G), где m(G) и m(A) — геометрические меры (длины, площади или объемы) всего пространства элементарных исходов G и события А соответственно

Чаще всего, в одномерном случае речь идет о длинах отрезков, в двумерном — о площадях фигур, а в трехмерном — об объемах тел.

Пример. Какова вероятность встречи с другом, если вы договорились встретиться в парке в промежутке с 12.00 до 13.00 и ждете друг друга 5 минут?

У нас есть отличное онлайн обучение по математике для учеников с 1 по 11 классы, записывайся на пробное занятие!

Сложение и умножение вероятностей

Теорема о сложении вероятностей звучит так: вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий:

P(A + B) = P(A) + P(B)

Эта теорема справедлива для любого числа несовместных событий:

Если случайные события A₁, A₂. A_n образуют полную группу несовместных событий, то справедливо равенство:

Произведением событий А и В называется событие АВ, которое наступает тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события.

Вторая теорема о сложении вероятностей: вероятность суммы совместных событий вычисляется по формуле:

P(A + B) = P(A) + P(B) − P(AB)

События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Теорема об умножении вероятностей: вероятность произведения независимых событий А и В вычисляется по формуле:

P(AB) = P(A) * P(B)

Пример. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8.

Найдем вероятности того, что формула содержится:

А — формула содержится в первом справочнике;

В — формула содержится во втором справочнике;

С — формула содержится в третьем справочнике.

Воспользуемся теоремами сложения и умножения вероятностей.

Ответ: 1 — 0,188; 2 — 0,452; 3 — 0,336.

Формула полной вероятности и формула Байеса

По теореме умножения вероятностей:

Аналогично, для остальных гипотез:

Эта формула называется формулой Байеса. Вероятности гипотез называются апостериорными вероятностями, тогда как — априорными вероятностями.

Пример. Одного из трех стрелков вызывают на линию огня, он производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго — 0,5; для третьего — 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком.

Формула Бернулли

При решении вероятностных задач часто бывает, что одно и тоже испытание повторяется многократно, и исход каждого испытания независит от исходов других. Такой эксперимент называют схемой повторных независимых испытаний или схемой Бернулли.

Примеры повторных испытаний:

Итак, пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы. А вероятность появления события А в каждом случае постоянна и не изменяется от испытания к испытанию.

Биномиальное распределение — распределение числа успехов (появлений события).

Пример. Среди видео, которые снимает блогер, бывает в среднем 4% некачественных: то свет плохой, то звук пропал, то ракурс не самый удачный. Найдем вероятность того, что среди 30 видео два будут нестандартными.

Опыт заключается в проверке каждого из 30 видео на качество. Событие А — это какая-то неудача (свет, ракурс, звук), его вероятность p = 0,04, тогда q = 0,96. Отсюда по формуле Бернулли можно найти ответ:

Ответ: вероятность плохого видео приблизительно 0,202. Блогер молодец🙂

Наивероятнейшее число успехов

Биномиальное распределение ( по схеме Бернулли) помогает узнать, какое число появлений события А наиболее вероятно. Формула для наиболее вероятного числа успехов k (появлений события) выглядит так:

Пример. В очень большом секретном чатике сидит 730 человек. Вероятность того, что день рождения наугад взятого участника чата приходится на определенный день года — равна 1/365 для каждого из 365 дней. Найдем наиболее вероятное число счастливчиков, которые родились 1 января.

Формула Пуассона

При большом числе испытаний n и малой вероятности р формулой Бернулли пользоваться неудобно. Например, 0.97 999 вычислить весьма затруднительно.

В этом случае для вычисления вероятности того, что в n испытаниях событие произойдет k раз, используют формулу Пуассона:

Здесь λ = np обозначает среднее число появлений события в n испытаниях.

Эта формула дает удовлетворительное приближение для p ≤ 0,1 и np ≤10.

События, для которых применима формула Пуассона, называют редкими, так как вероятность, что они произойдут — очень мала (обычно порядка 0,001-0,0001).

При больших np рекомендуют применять формулы Лапласа, которую рассмотрим чуть позже.

Пример. В айфоне 1000 разных элементов, которые работают независимо друг от друга. Вероятность отказа любого элемента в течении времени Т равна 0,002. Найти вероятность того, что за время Т откажут ровно три элемента.

P₁₀₀₀(3) = λ 3 /3! * e −λ = 2 3 /3! * e −2 ≈ 0,18.

Ответ: ориентировочно 0,18.

Теоремы Муавра-Лапласа

Кроме того, пусть P_n(k₁;k₂) — вероятность того, что число появлений события А находится между k₁ и k₂.

Локальная теорема Лапласа звучит так: если n — велико, а р — отлично от 0 и 1, то

Интегральная теорема Лапласа звучит так: если n — велико, а р — отлично от 0 и 1, то

Функции Гаусса и Лапласа обладают свойствами, которые пригодятся, чтобы правильно пользоваться таблицей значений этих функций:

Теоремы Лапласа дают удовлетворительное приближение при npq ≥ 9. Причем чем ближе значения q, p к 0,5, тем точнее данные формулы. При маленьких или больших значениях вероятности (близких к 0 или 1) формула дает большую погрешность по сравнению с исходной формулой Бернулли.

Источник

ИСПЫТАНИЕ

Смотреть что такое «ИСПЫТАНИЕ» в других словарях:

ИСПЫТАНИЕ — ИСПЫТАНИЕ, испытания, ср. (книжн.). 1. только ед. Действие по гл. испытать, проверка, исследование каких нибудь качеств, пригодности к чему нибудь. Испытание материалов. Испытание двигателя. Отправить в госпиталь на испытание. Быть на испытании.… … Толковый словарь Ушакова

испытание — Определение одной или нескольких характеристик согласно установленной процедуре. [ГОСТ Р ИСО 9000 2008] испытание Экспериментальное определение количественных и (или) качественных характеристик свойств объекта испытаний как результата воздействия … Справочник технического переводчика

ИСПЫТАНИЕ — понятие теории вероятностей. Испытание может иметь один (и только один) из n исходов. Каждый исход испытания рассматривается как случайное событие, имеющее определенную вероятность … Большой Энциклопедический словарь

испытание — ИСПЫТАНИЕ, диагностика, опробование, проба, проверка, тест ИСПЫТЫВАТЬ/ИСПЫТАТЬ, несов. и сов. диагностировать, сов. опробовать, проверять/проверить, несов. и сов. тестировать … Словарь-тезаурус синонимов русской речи

Испытание — – определение одной или нескольких характеристик согласно установленной процедуре. [ГОСТ Р ИСО 9000 2008] Испытание – экспериментальное определение количественных и (или) качественных характеристик свойств объекта испытаний как… … Энциклопедия терминов, определений и пояснений строительных материалов

Испытание — А. Проверка качества или заявленных свойств предмета. Б. Контрольный опрос, экзамен, тест. Словарь бизнес терминов. Академик.ру. 2001 … Словарь бизнес-терминов

ИСПЫТАНИЕ — ИСПЫТАНИЕ, я, ср. 1. см. испытать. 2. Проверочный опрос или экзамен. Приёмные испытания. 3. Тягостное переживание, несчастье. Тяжёлое и. Суровые испытания войны. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

Испытание — Братья, Драупади и Кунти уже не чаяли увидеть Арджуну, считая его погибшим, когда он в диадеме, сверкающей драгоценными камнями, опустился прямо с неба на колеснице в их объятья. И не было им конца. После того как все насытились радостью… … Энциклопедия мифологии

ИСПЫТАНИЕ — на прочность. Публ. Проверка сил, выдержки, выносливости человека в экстремальных ситуациях. Ф 1, 225; Мокиенко 2003, 38 … Большой словарь русских поговорок

Испытание — техническая операция, заключающаяся в установлении характеристик продукции, процесса или услуги … Российская энциклопедия по охране труда

Источник