что такое искомая фигура

Значение слова «искомый»

Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

ИСКО’МЫЙ, ая, ое (книжн.). 1. Подлежащий определению посредством вычислений (мат.). И. коэфициент. Искомая величина. Искомое выражение. 2. в знач. сущ. иско́мое, ого, ср. Величина, к-рую следует определить посредством вычислений (мат.). Найти искомое. 3. Требуемый, подлежащий установлению. Рассуждая так, мы придем к искомому выводу.

Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека

иско́мый

1. подлежащий поиску, разыскиваемый ◆ Здесь внезапно заметили мы, что едем уже не по льду, а по твёрдой земле, и сначала полагали, что открыли искомый остров. 〈…〉 Горы тянулись к юго-западу, а на юге лежала пространная долина, где изгибался предел наших страданий ― давно искомый Анюй. Ф. П. Врангель, «Путешествие по северным берегам Сибири и по Ледовитому морю», 1841 г. (цитата из НКРЯ)

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я стал чуточку лучше понимать мир эмоций.

Вопрос: тромбоциты — это что-то нейтральное, положительное или отрицательное?

Источник

Как найти координаты точки?

3 класс, 4 класс, 9 класс, 11 класс, ЕГЭ/ОГЭ

Понятие системы координат

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.

Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

Определение координат точки

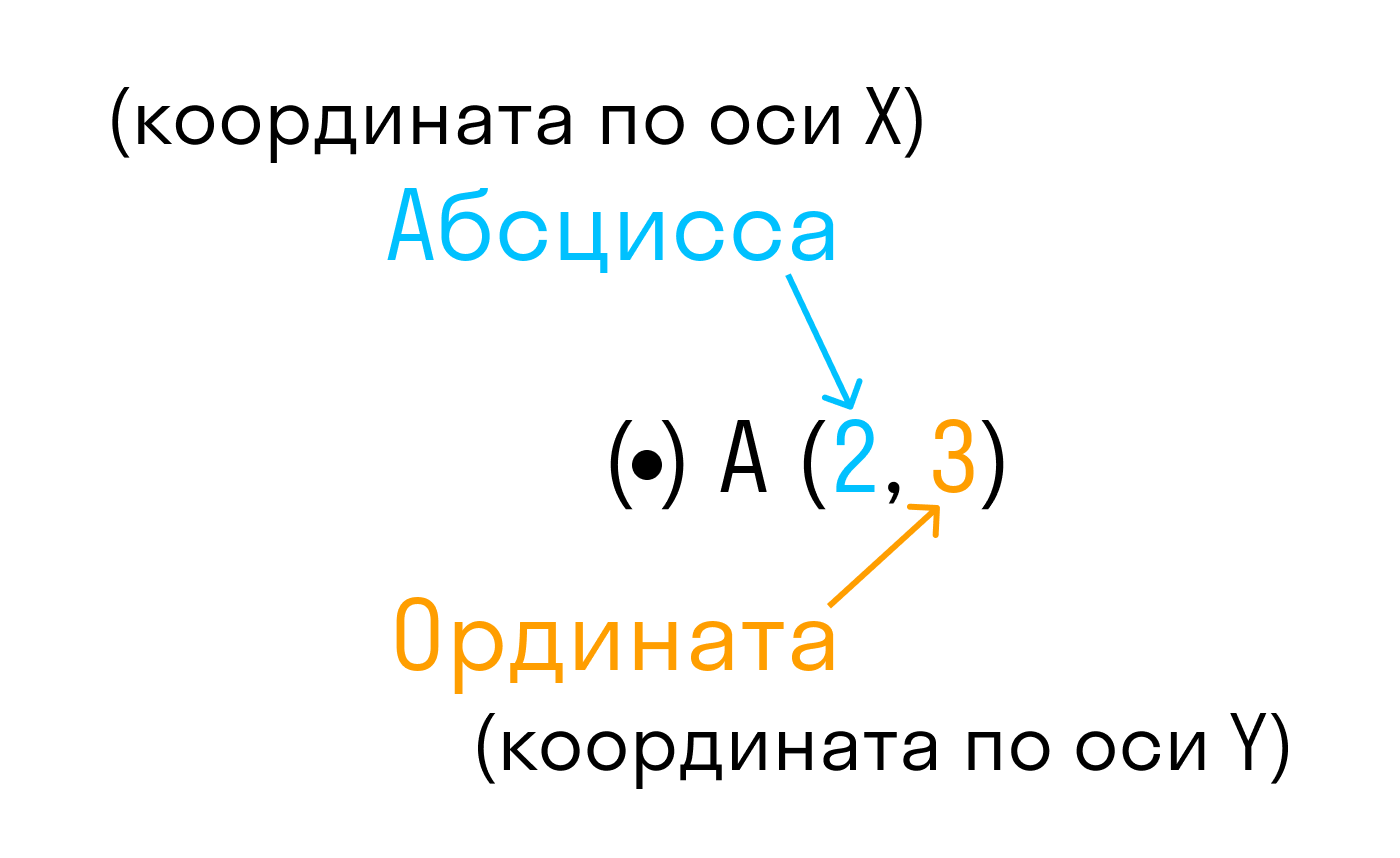
Каждой точке координатной плоскости соответствуют две координаты.

Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.

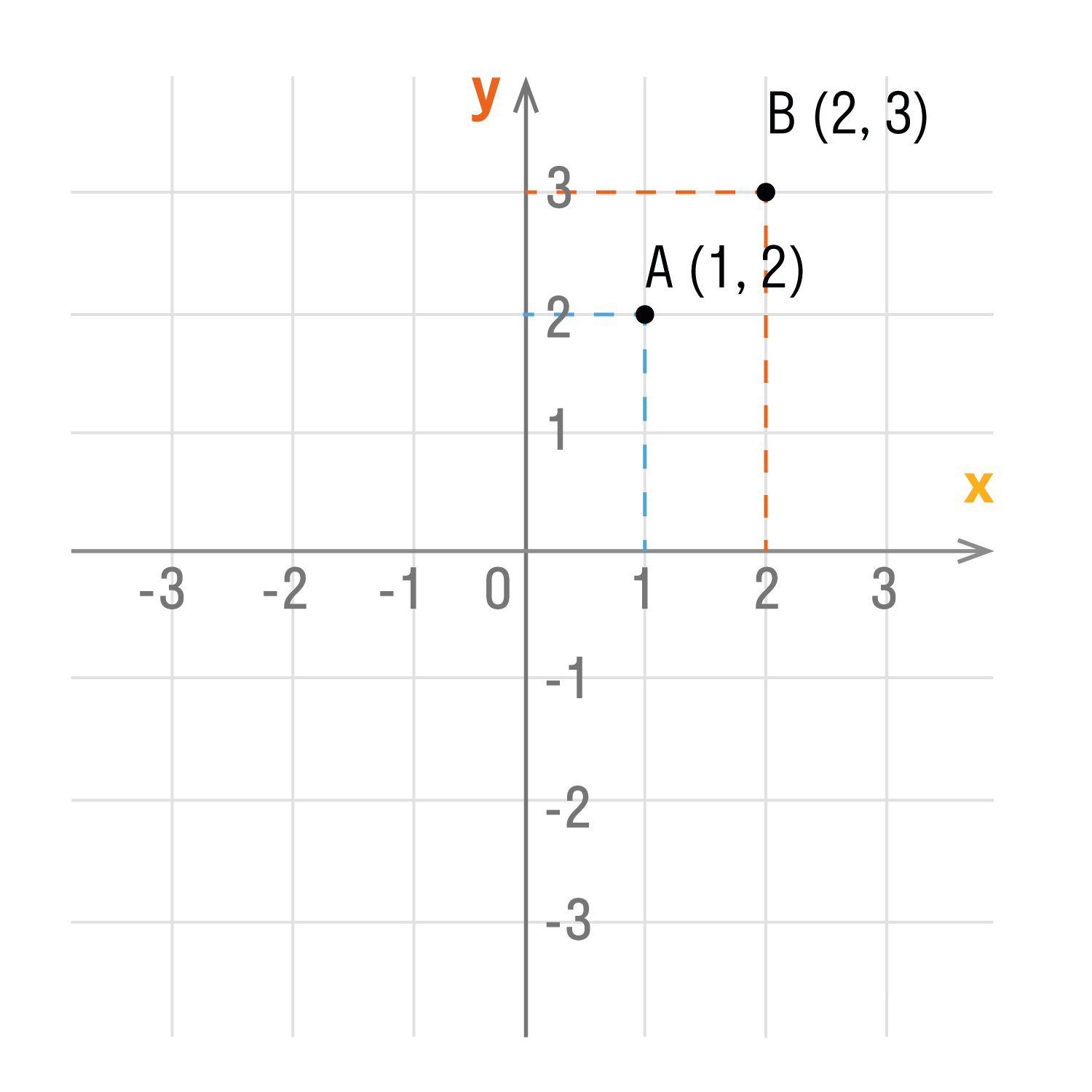
Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.

Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.

Смотрим на график и фиксируем: A (1; 2) и B (2; 3).

Особые случаи расположения точек

В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:

Способы нахождения точки по её координатам

Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.

Способ первый. Как определить положение точки D по её координатам (-4, 2):

Способ второй. Как определить положение точки D (-4, 2):

Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:

Источник

Большая Энциклопедия Нефти и Газа

Искомая фигура

Искомая фигура KLMN равновелика фигуре, заштрихованной на рнс. [1]

Предполагают искомую фигуру уже известной и с помощью методов, к рассмотрению которых мы сейчас приступим, изучают фигуру до тех пор, пока не станет ясным тот путь, по которому задача может быть решена предложенными средствами решения. [2]

Для построения искомой фигуры следует взять в плоскости подобия, совмещенной с плоскостью чертежа. Со, принимаемые за соответствующие точкам А, В и С. Остальные точки двух последних фигур строятся как аффинно-соответствующие точкам фронтальной проекции фигуры. [3]

Заданные элементы искомой фигуры в задачах на построение большей частью фактически не задаются, а лишь указываются. В приведенной задаче сказано, что даны прямая / и точка А вне ее, но фактически ни прямая /, ни точка А не даны. Мы можем их провести где и как угодно. В рассматриваемой задаче это, конечно, совершенно несущественно. [4]

Заданные элементы искомой фигуры в задачах на построение большей частью фактически не задаются, а лишь указываются. В приведенной задаче сказано, что даны прямая / и точка А вне ее, но фактически ни прямая /, ни точка А не даны. Мы можем их провести где и как угодно. В рассматриваемой задаче это, конечно, совершенно несущественно. [5]

Наряду с данными и искомыми фигурами рассматриваем фигуры, инверсные им или их частям. Иногда этого оказывается уже достаточно для нахождения таких связей между искомыми и данными, которые нужны для решения задачи. [6]

Натуральная величина Ф [ искомой фигуры состоит в аффинном соответствии с фигурой Ф2, так как они подобны. Без этого необходимого условия задачи не имеют решения. [7]

В задачах этого рода положение искомой фигуры остается произвольным; но во многих вопросах требуется построить фигуру, положение которой относительно данных точек или линий вполне определено. При этом может случиться, что, отрешившись от какого-нибудь одного из условий положения и оставив все остальные, мы получим бесчисленное множество фигур, подобных искомой. В таком случае метод подобия может быть употреблен с пользой. [8]

Сначала установим данные элементы, искомую фигуру и те свойства, которыми она должна обладать. [9]

После построения вспомогательной фигуры и обратного Ьереноса получаем искомую фигуру с помощью ряда простейших построений или непосредственно. [11]

К и Я2 2 радиусом, равным 4, Искомая фигура TNKiRHzLT обведена жирной линией. [13]

Этот метод оказывается наиболее полезным, когда непосредственное построение искомой фигуры затруднительно в связи с разобщенностью ее элементов. [15]

Источник

Большая Энциклопедия Нефти и Газа

Искомая фигура

Итак, если условие задачи не предусматривает определенного расположения искомой фигуры относительно данных фигур то условимся искать только все неравные между собой фигуры, удовлетворяющие условиям задачи. Это означает, что задача считается решенной, если: 1) построено некоторое число неравных между собой фигур Фр ФЕ удовлетворяющих условиям задачи, и 2) доказано, что всякая фигура, удовлетворяющая условиям задачи, равна одной из этих фигур. При этом считается, что задача имеет п различных решений. [18]

Иногда задача не имеет решений потому, что на искомую фигуру наложено слишком много условий. Например, нельзя, вообще говоря, построить окружность, проходящую через четыре заданные точки, или построить треугольник, зная три его стороны и один из углов. Задачи такого рода называются переопределенными. [19]

Иногда ставится также задача: выяснить, при каких условиях искомая фигура будет удовлетворять тем или иным дополнительным требованиям. Например, может быть поставлен вопрос: при каких условиях искомый треугольник будет прямоугольным или равнобедренным. [21]

В других методах на данных фигурах или каких-нибудь построениях строится искомая фигура или делается какое-либо построение. В методе же обратности на искомой фигуре или на искомых построениях строятся данные фигуры, а затем переносятся на данные фигуры. Иногда на искомом построении приходится строить фигуры не равные, а подобные данным фигурам; построенную фигуру остается перенести на данные фигуры ( Александров И.И. Сборник геометрических задач на построение. [22]

Метод заключается в том, что, повернув какую-либо данную или искомую фигуру вокруг некоторого центра на некоторый угол, анализ рассматриваемой фигуры сводят к анализу более простой фигуры, а потом выполняют обратное вращение и в результате получают искомую фигуру. Центр и угол поворота следует выбирать так, чтобы в результате поворота совместились элементы одинаковой величины. [24]

Предположив, что задача решена, делают от руки приблизительный чертеж: искомой фигуры и затем, внимательно рассматривая начерченную фигуру, стремятся найти такие зависимости между данными задачи и искомыми, которые позволили бы свести задачу к другим, известным ранее. Эта самая важная часть решения задачи, имеющая целью составить план решения, носит название анализа. [26]

Правильность решения задачи на построение по планиметрии ( с параметрами) проверяется путем построения искомой фигуры при различных значениях данных параметров. [27]

Источник

Основные геометрические фигуры

Основные понятия

Основные геометрические фигуры на плоскости — это точка и прямая линия. А простейшие фигуры — это луч, отрезок и ломаная линия.

Минимальный объект в геометрии — точка. Ее особенность в том, что она не имеет размеров: у нее нет высоты, длины, радиуса. У точки можно определить только ее расположение, которое принято обозначать одной заглавной буквой латинского алфавита.

Из множества точек может получится линия, а из нескольких соединенных между собой линий — геометрические фигуры.

Каждая математическая фигура имеет собственную величину, которую можно измерить при помощи формул и внимательности.

Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.

Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской P.

Если параметры переданы в разных единицах измерения длины, нужно перевести все данные к одной единице измерения.

Популярные единицы измерения площади:

Геометрические тела — часть пространства, которая ограничена замкнутой поверхностью своей наружной границы.

Если все точки фигуры принадлежат одной плоскости, значит она является плоской.

Объемная фигура — геометрическая фигура, у которой все точки не находятся на одной плоскости.

Примеры объемных геометрических фигур:

Рассмотрим подробнее некоторые фигуры, разберем их определения и свойства.

Прямоугольник

Прямоугольник — четырехугольник, у которого все стороны пересекаются под прямым углом.

Узнать площадь прямоугольника помогут следующие формулы:

Диагональ — это отрезок, который соединяет противоположные вершины фигуры. Он есть во всех фигурах, число вершин которых больше трех.

Периметр прямоугольника — сумма длины и ширины, умноженная на два.

P = 2 × (a + b), где a — ширина, b — высота.

Квадрат

Квадрат — это тот же прямоугольник, у которого все стороны равны.

Найти площадь квадрата легко:

Периметр квадрата — это длина стороны, умноженная на четыре.

P = 4 × a, где a — длина стороны.

Трапеция

Трапеция — это четырехугольник, у которого две стороны параллельны, а две не параллельны.

Основное свойство: в трапецию можно вписать окружность, если сумма ее оснований равна сумме боковых сторон.

Как найти площадь трапеции:

S = (a + b) : 2 × h, где a, b — два разных основания, h — высота трапеции.

Построить высоту трапеции можно, начертив отрезок так, чтобы он соединил параллельные стороны и был расположен перпендикулярно к этим основаниям.

Формула периметра для равнобедренной трапеции отличается от прямоугольника тем, что у равнобедренной трапеции есть две равные стороны.

P = a + b + 2 × c, где a, b — параллельные стороны, c — две длины одинаковых сторон.

Параллелограмм и ромб

Параллелограмм — четырехугольник, противоположные стороны которого попарно параллельны

Ромб — это параллелограмм с равными сторонами.

Общие формулы расчета площади фигур:

Периметр ромба — это произведение длины стороны на четыре.

P = 4 × a, где a — длина стороны.

Периметр параллелограмма — сумма длины и ширины, умноженная на два.

P = 2 × (a + b), где a — ширина, b — высота.

Треугольник

Треугольник — это такая фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки принято называть вершинами, а отрезки — сторонами.

Рассчитать площадь треугольника можно несколькими способами по исходным данным, давайте их рассмотрим.

S = 0,5 × a × h, где a — длина основания, h — высота, проведенная к основанию.

Основание может быть расположено иначе, например так:

При тупом угле высоту можно отразить на продолжение основания:

При прямом угле основанием и высотой будут его катеты:

S = 0,5 × a × b × sinα, где a и b — две стороны, sinα — синус угла между ними.

S = (a × b × с) : 4 × R, где a, b и с — стороны треугольника, а R — радиус описанной окружности.

S = p × r, где р — полупериметр треугольника, r — радиус вписанной окружности.

Периметр треугольника — это сумма длин трех его сторон.

P = a + b + c, где a, b, c — длина стороны.

Формула измерения периметра для равностороннего треугольника — это длины стороны, умноженная на три.

P = 3 × a, где a — длина стороны.

Круг — это множество точек на плоскости, которые удалены от центра на равном радиусу расстоянии.

Окружность — это граница круга.

Радиус окружности — это расстояние от центра окружности до любой точки на ней.

Диаметр круга — это отрезок, который соединяет две точки на окружности и проходящий через ее центр. Диаметр круга равен двум его радиусам.

Формулы площади круга:

Периметр круга или длина окружности — это произведение радиуса на два Пи или произведение диаметра на Пи.

L = d × π = 2 × r × π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Источник