что такое инцентр треугольника
Инцентр
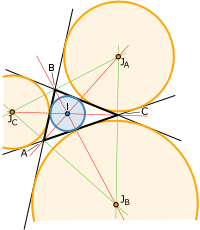
Инцентр — точка пересечения биссектрис треугольника. Также инцентр является центром вписанной в треугольник окружности (откуда и название).
Традиционно обозначается латинской буквой 
.
Свойства
См. также
Литература
Полезное
Смотреть что такое «Инцентр» в других словарях:
Геометрия треугольника — Эта статья предлагается к удалению. Пояснение причин и соответствующее обсуждение вы можете найти на странице Википедия:К удалению/13 октября 2012. Пока процесс обсужден … Википедия
Ортоцентр — (от греч. ορθοξ прямой) точка пересечения высот треугольника или их продолжений. Традиционно обозначается латинской буквой H. В зависим … Википедия
Список объектов, названных в честь Леонарда Эйлера — Существует множество математических и физических объектов, названных в честь Леонарда Эйлера: Содержание 1 Теоремы 2 Лемма 3 Уравнения 4 … Википедия
Центроид — центр масс фигуры, например, точка пересечения медиан в треугольнике. Центроид традиционно обозначается латинской буквой M … Википедия
Центр фигуры — в планиметрии, в зависимости от контекста может означать: Центр симметрии Центр масс Кроме того, если фигура треугольник: Ортоцентр (от греч. ορθοξ прямой) точка пересечения высот Инцентр точка пересечения биссектрис Центроид точка пересечения… … Википедия
Замечательные точки треугольника — Замечательные точки треугольника точки, местоположение которых однозначно определяется треугольником и не зависит от того, в каком порядке берутся стороны и вершины треугольника. Обычно они расположены внутри треугольника, но и это не… … Википедия
Ортоцентрическая система — Ортоцентр (от греч. ορθοξ прямой) точка пересечения высот треугольника или их продолжений. Традиционно обозначается латинской буквой H. В зависимости от вида треугольника ортоцентр может находится внутри треугольника (в остроугольных), вне его (в … Википедия
Центр (геометрия) — Центр фигуры в планиметрии, в зависимости от контекста может означать: Центр симметрии Центр масс Кроме того, если фигура треугольник: Ортоцентр (от греч. ορθοξ прямой) точка пересечения высот Инцентр точка пересечения биссектрис Центроид точка… … Википедия
Центр (середина) — Центр фигуры в планиметрии, в зависимости от контекста может означать: Центр симметрии Центр масс Кроме того, если фигура треугольник: Ортоцентр (от греч. ορθοξ прямой) точка пересечения высот Инцентр точка пересечения биссектрис Центроид точка… … Википедия
Центроид треугольника — Центроид точка пересечения медиан в треугольнике. Центроид традиционно обозначается латинской буквой … Википедия
Вписанная и вневписанная окружности треугольника
Incenter
Трехлинейные координаты
Эти координаты трилинейных для точки в треугольнике есть отношение всех расстояний до сторон треугольника. Поскольку центр центра находится на одинаковом расстоянии от всех сторон треугольника, трилинейные координаты центра центра равны [6]
Барицентрические координаты
В барицентрических координатах для точки в треугольнике Дайте весы таким образом, что точка является взвешенным средним позиций треугольника вершин. Барицентрические координаты инцентратора даются [ цитата ]
Декартовы координаты
Радиус
Расстояния до вершин
Прочие свойства
Вписанная окружность и ее свойства радиуса
Расстояния между вершиной и ближайшими точками касания
Расстояния от вершины до двух ближайших точек касания равны; например: [10]
Прочие свойства
а площадь треугольника равна
Некоторые соотношения между сторонами, радиусом вписанной окружности и радиусом описанной окружности: [13]
Любая линия, проходящая через треугольник, которая разделяет площадь треугольника и его периметр пополам, проходит через центр треугольника (центр вписанной окружности). Для любого треугольника их может быть один, два или три. [14]
Радиус вписанной окружности не превышает одной девятой суммы высот. [17] : 289
Центр находится в среднем треугольнике (вершины которого являются серединами сторон). [18] : 233, лемма 1.
Отношение к площади треугольника
Треугольник Жергонна и точка
Точка Жергонна треугольника имеет ряд свойств, в том числе то, что она является симедианной точкой треугольника Жергонна. [23]
Трилинейные координаты для вершин треугольника касания задаются [ ссылка ]
Трилинейные координаты для точки Жергонна даются [ ссылка ]
Трехлинейные координаты эксцентров
Exradii
Вывод формулы exradii [27]
Прочие свойства
Из приведенных выше формул видно, что вневписанная окружность всегда больше, чем вписанная, и что наибольшая вневписанная окружность касается самой длинной стороны, а наименьшая вневписанная окружность касается самой короткой стороны. Далее, объединение этих формул дает: [28]
Другие свойства вневписанной окружности
Треугольник Нагеля и точка Нагеля
Три линии А Т А <\ displaystyle AT_ > 
, B Т B <\ displaystyle BT_ > а также C Т C <\ displaystyle CT_ называются разделителями треугольника; каждая из них делит пополам периметр треугольника, [ цитата необходима ]
Разделители пересекаются в одной точке, точка Нагеля треугольника N а <\ displaystyle N_ > (или центр треугольника X 8 ).
Трилинейные координаты для вершин треугольника вне касания задаются [ ссылка ]
Трилинейные координаты точки Нагеля даются [ ссылка ]
Точка Нагеля изотомно сопряжена с точкой Жергонна. [ необходима цитата ]
Девятиточный круг и точка Фейербаха
Внутренний и эксцентральный треугольники
Excentral треугольник опорного треугольника имеет вершины в центрах Вневписанных эталонного треугольника. Его стороны находятся на биссектрисах внешнего угла опорного треугольника (см. Рисунок вверху страницы ). Трилинейные координаты вершин эксцентрального треугольника задаются формулой [ необходима цитата ]
Теорема Эйлера утверждает, что в треугольнике:
Для вневписанных кругов уравнение аналогично:
Что такое элементы треугольника?
Содержание:
Первичные элементы соответствуют вершинам, сторонам и углам, они могут быть внутренними или внешними.
Второстепенные относятся к высоте, ортоцентру, биссектрисе, центру, биссектрисе, центру описанной окружности и медиане. Обычно в тригонометрии время уделяется только изучению основных элементов и дополнительно к высоте.
Основные элементы треугольника
Когда дело доходит до изучения геометрических фигур, треугольники играют ключевую роль, поскольку они считаются простейшими существующими многоугольниками, поскольку у них всего 3 стороны. Любой многоугольник с 4 или более сторонами можно разделить на конечное число треугольников.
Вершины
Они являются исходными точками треугольника. Визуально вершину можно определить как место, где рождаются линии многоугольника и которые определяют его границы.
Их легко узнать, так как они определяют общий размер фигуры. Обычно их обозначают заглавными буквами A, B и C.
Стороны
Обычно они обозначаются буквами вершин на концах, например сторона AB, или строчными буквами a, b и c, расположив их на противоположной стороне вершин A, B и C.
Сумма длин сторон треугольника называется периметром.
Углы
Это степень разделения двух сторон, начинающихся от одной и той же вершины (внутренний угол), измеряется в градусах.
Сумма всех углов в треугольнике всегда 180 градусов. Также можно измерить внешний угол, в этом случае необходимо удлинить одну из сторон.
Углы обозначаются греческими буквами, такими как альфа (α), бета (β) или гамма (γ).
Высота
Это мера перпендикулярной линии (которая образует угол в 90 градусов), которая проходит от одной вершины к противоположной стороне.
Оно обозначается строчной буквой h. Треугольник может иметь 3 разных высоты в зависимости от измеряемой вершины.
Ортоцентр
При нанесении трех высот треугольника точка, в которой соприкасаются три линии, является ортоцентром. Обычно обозначается буквой H.
Биссектриса
Это линия, идущая от одной вершины к центру противоположной стороны треугольника, поэтому она «делит» угол пополам. В зависимости от типа треугольника высота и биссектриса могут быть одинаковыми.
Incenter
Это точка, где встречаются 3 биссектрисы.
Медиатр
Также известная как симметричная линия, это линия, перпендикулярная одной стороне треугольника, проходящая через его середину.
Окружной центр
Это общая точка пересечения трех медиатрис. Если нарисовать круг, который касается трех вершин треугольника, центр описанной окружности будет центром круга.
Медиана
Это линия, соединяющая середины двух сторон.
Ссылки
Возрастные комплексы: что это такое и как их преодолеть
Эпендимные клетки: гистология, типы и функции