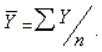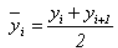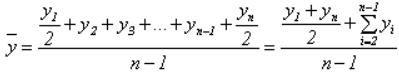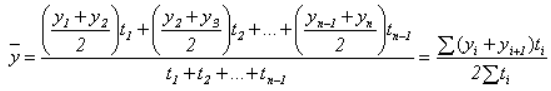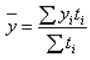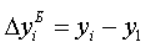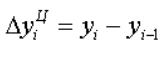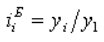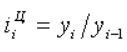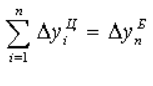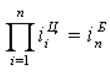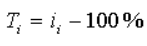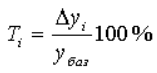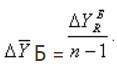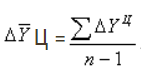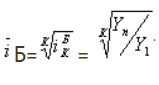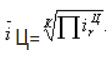что такое интервальный ряд динамики тест

Что такое интервальный ряд динамики тест

1.Что такое динамический ряд?

1. Динамический ряд—это множество единиц изучаемого явления, объединенных общими свойствами и подвергающихся дальнейшему изучению.

2. Динамический ряд – это величина, отображающая относительные размеры социально-экономических явлений.

3. Динамический ряд—это упорядоченная совокупность данных, в которых каждому значению признака (варианте или интервалу) соответствует определённое значение частоты или частости.

4. Динамический ряд—это ряд числовых значений признака, представленных в хронологической последовательности и отражающий меру развития явления и процесса, за определённый период времени или на отдельные даты.

5. Динамический ряд—это относительно количественный показатель, получаемый путём сопоставления совокупностей, состоящих из несоизмеримых элементов( не поддающихся прямому суммированию) и отражающих изменение во времени или в пространстве.

2.В зависимости от времени, к которому относится динамический ряд различают:

1. Моментные динамические ряды.

2. Детерминированные динамические ряды.

3. Интервальные динамические ряды.

4. Сложносоставные динамические ряды.

5. Динамические ряды с абсолютными величинами.

3. К механическим приёмам выравнивания относится:

1. Метод по среднему абсолютному приросту.

2. Метод укрупнения периодов.

3. Метод наименьших квадратов.

4. Метод скользящей средней.

5. Метод по среднегодовому темпу роста.

4. Какой из аналитических приёмов выравнивания является наиболее распространенным?

1. По среднему абсолютному приросту.

2. По среднегодовому темпу роста.

3. Метод наименьших квадратов.

4. Метод скользящей средней.

5. Метод укрупнения периодов.

5. В зависимости от величин, которыми представлены уровни динамического ряда, различают динамические ряды:

Источник

Ряды динамики в статистике

9.1. Понятие и виды рядов динамики

Ряд значений статистического показателя, расположенных в хронологическом порядке и характеризующих развитие явления во времени, называется рядом динамики. Примеры рядов динамики приведены в табл. 9.1-9.4.

Таблица 9.1. Число предприятий и организаций в Российской Федерации, тыс. (по состоянию на 1 января)

Год	2001	2002	2003	2004	2005	2006
Число предприятий и организаций, тыс.	3 347	3 594	3 845	4 150	4 414	4 767

Таблица 9.2. Удельный вес предприятий и организаций частной формы собственности в общей совокупности предприятий и организаций Российской Федерации за период 2002-2006 гг.

Год	2002	2003	2004	2005	2006
Удельный вес предприятий и организаций частной формы собственности, %	75,8	76,9	78,0	79,2	80,5

Таблица 9.3. Индексы физического объема оборота розничной торговли в Российской Федерации(в процентах к предыдущему году)

Год	2000	2001	2002	2003	2004	2005
Индекс оборота розничной торговли	109	111	109	109	113	113

Таблица 9.4. Показатели деятельности рекламных агентств в Российской Федерации за период 1999-2002 гг.

Показатель	Год
1999	2000	2001	2002
Число рекламных агентств (на конец года): всего	2 325	1 957	1 576	1 756
В процентах к предыдущему году	200	84	51	111
Среднесписочная численность работников в расчете на одно рекламное агентство, чел.	10	10	12	16
Выручка от реализации рекламных услуг в расчете на одного работника, тыс. руб.	166	311	364	543

Данные о количестве предприятий и организаций Российской Федерации (см. табл. 9.1) относятся к 1 января каждого года, поэтому данный ряд является моментным.

Динамический ряд, представленный в табл. 9.4 и характеризующий выручку от реализации рекламных услуг в расчете на одного работника, является интервальными, поскольку содержит значения показателя за годовые промежутки времени.

Деление динамических рядов на моментные и интервальные обусловлено разными методологическими подходами, применяемыми к их анализу, поэтому всегда следует обращать внимание, к какому виду относится исследуемый ряд.

В зависимости от вида статистического показателя динамические ряды подразделяют на ряды абсолютных, относительных и средних величин.

Ряды абсолютных величин являются исходными для построения рядов динамики относительных и средних величин.

Динамические ряды относительных величин могут содержать информацию об изменении удельных весов какого-либо показателя в общей совокупности объектов за определенный временной период (см. табл. 9.2), индексов (см. табл. 9.3); темпов роста показателя за определенный период времени (см. табл. 9.4, данные строки «Число рекламных агентств, в процентах к предыдущему году»); изменение во времени показателей интенсивности, например демографических коэффициентов: смертности, рождаемости, брачности, разводимости, естественного прироста и т.д.

В зависимости от расстояния во времени различают ряды динамики с равноотстоящими уровнями и неравноотстоящими уровнями. Методы анализа таких рядов также различаются между собой.

При построении динамического ряда следят за тем, чтобы его уровни отвечали требованиям сопоставимости: характеризовали один и тот же объект или явление, относились к одной и той же территории, к сопоставимому периоду времени, были рассчитаны по единой методологии с одинаковыми единицами измерения значений этого показателя.

Пример 9.1. Рассмотрим

Таблица 9.5. Данные о числе малых предприятий одного из городов Российской Федерации за период 1999-2006 гг.

Показатель	Год
1999	2000	2001	2002	2003	2004	2005	2006
Количество малых предприятий:
— по старой методологии отнесения к кругу малых предприятий	54	89	125	—	—	—	—	—
— по новой методологии отнесения к кругу малых предприятий	—	—	90	138	169	194	206	220
Сомкнутый динамический ряд абсолютных величин (по новой методологии)	39	64	90	138	169	194	206	220
Сомкнутый динамический ряд относительных величин, в % к 1995 г.	43	71	100	153	188	215	229	244

Произведем смыкание двух динамических рядов в один. Для получения ряда абсолютных величин произведем следующие действия:

Сомкнутый ряд динамики относительных величин позволяет получить представление о темпах развития малого предпринимательства за весь рассматриваемый период.

Источник

Ряды динамики

Понятие рядов динамики (временных рядов)

Одной из важнейших задач статистики является изучение изменений анализируемых показателей во времени, то есть их динамика. Эта задача решается при помощи анализа рядов динамики (временных рядов).

Ряд динамики (или временной ряд) – это числовые значения определенного статистического показателя в последовательные моменты или периоды времени (т.е. расположенные в хронологическом порядке).

Числовые значения того или иного статистического показателя, составляющего ряд динамики, называют уровнями ряда и обычно обозначают буквой y. Первый член ряда y₁ называют начальным или базисным уровнем, а последний y_n – конечным. Моменты или периоды времени, к которым относятся уровни, обозначают через t.

Ряды динамики, как правило, представляют в виде таблицы или графика, причем по оси абсцисс строится шкала времени t, а по оси ординат – шкала уровней ряда y.

Пример ряда динамики

Таблица. Число жителей России в 2004-2009 гг. в млн.чел, на 1 января

Год	2004	2005	2006	2007	2008	2009
Число жителей	144,2	143,5	142,8	142,2	142,0	141,9

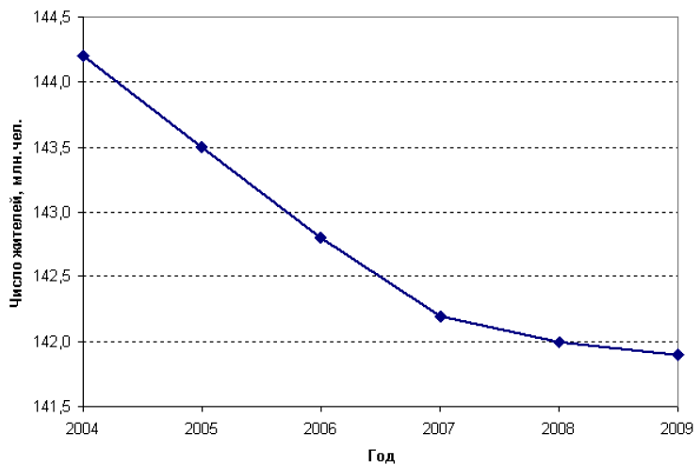
График ряда динамики числа жителей России в 2004-2009 гг. в млн.чел, на 1 января

Данные таблицы и графика наглядно иллюстрируют ежегодное снижение числа жителей России в 2004-2009 годах.

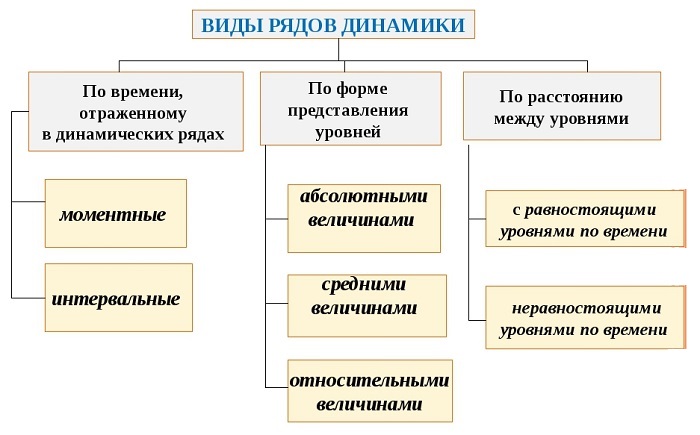
Виды рядов динамики

Ряды динамики классифицируются по следующим основным признакам:

В нашем примере про число жителей России ряд динамики: 1) моментный (приведены уровни на 1 января); 2) абсолютных величин (в млн.чел.); 3) равномерный (равные интервалы в 1 год); 4) изолированный.

Показатели изменения уровней ряда динамики

Анализ рядов динамики начинается с определения того, как именно изменяются уровни ряда (увеличиваются, уменьшаются или остаются неизменными) в абсолютном и относительном выражении. Чтобы проследить за направлением и размером изменений уровней во времени, для рядов динамики рассчитывают показатели изменения уровней ряда динамики:

Все эти показатели могут определяться базисным способом, когда уровень данного периода сравнивается с первым (базисным) периодом, либо цепным способом – когда сравниваются два уровня соседних периодов.

Базисное абсолютное изменение представляет собой разность конкретного и первого уровней ряда, определяется по формуле

Оно показывает, на сколько (в единицах показателей ряда) уровень одного (i-того) периода больше или меньше первого (базисного) уровня, и, следовательно, может иметь знак «+» (при увеличении уровней) или «–» (при уменьшении уровней).

Цепное абсолютное изменение представляет собой разность конкретного и предыдущего уровней ряда, определяется по формуле

Оно показывает, на сколько (в единицах показателей ряда) уровень одного (i-того) периода больше или меньше предыдущего уровня, и может иметь знак «+» или «–».

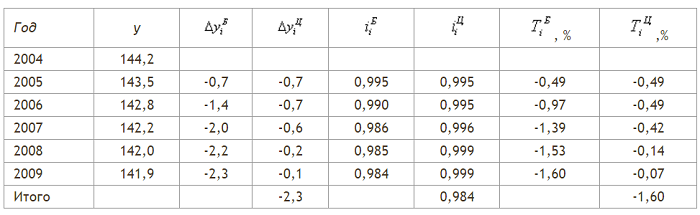
В следующей расчетной таблице в столбце 3 рассчитаны базисные абсолютные изменения, а в столбце 4 – цепные абсолютные изменения.

Год	y					, %	,%
2004	144,2
2005	143,5	-0,7	-0,7	0,995	0,995	-0,49	-0,49
2006	142,8	-1,4	-0,7	0,990	0,995	-0,97	-0,49
2007	142,2	-2,0	-0,6	0,986	0,996	-1,39	-0,42
2008	142,0	-2,2	-0,2	0,985	0,999	-1,53	-0,14
2009	141,9	-2,3	-0,1	0,984	0,999	-1,60	-0,07
Итого	-2,3	0,984	-1,60

Между базисными и цепными абсолютными изменениями существует взаимосвязь: сумма цепных абсолютных изменений равна последнему базисному изменению, то есть

.

Базисное относительное изменение (базисный темп роста или базисный индекс динамики) представляет собой соотношение конкретного и первого уровней ряда, определяясь по формуле

Цепное относительное изменение (цепной темп роста или цепной индекс динамики) представляет собой соотношение конкретного и предыдущего уровней ряда, определяясь по формуле

.

Относительное изменение показывает во сколько раз уровень данного периода больше уровня какого-либо предшествующего периода (при i>1) или какую его часть составляет (при i Следующая лекция.

Источник

Ряды динамики в статистике помогают отслеживать и анализировать изменение каких-либо собранных показателей с течением временем.

Форма представления может отличаться, но принципы обработки остаются неизменными.

Понятие ряда динамики в статистике

Подразумевается совокупность чисел, описывающая состояние интересующего фактора. При этом должна соблюдаться хронологическая последовательность с образованием временного ряда.

Ряд может быть подан в виде таблицы. Например, ниже указано население в миллионах человек по годам на 1-е февраля.

Представляется более наглядной и динамической графическая интерпретация, показанная на рисунке ниже:

Виды рядов динамики в статистике

Разделяют последовательности по временным показателям и по представлению чисел:

Отсечка производится по конкретному отрезку времени (моментный ряд) или суммируется за какой-то промежуток (интервальный ряд). В приведенном примере – первый случай. Показано состояние на определенную дату. Попытка что-то просуммировать даст бессмысленное число. Второй способ актуален, если, например, характеризуется выпуск товаров за неделю, месяц, квартал.

С постоянным или изменяющимся временным отрезком. В нашем случае отображаются регулярные годовые замеры.

Показаны абсолютные, средние или относительные безразмерные числа. У нас иллюстрируется количество живущих в государстве людей без каких-либо алгебраических вмешательств.

По сути показателей. Может сопоставляться курс валюты (одномерный критерий), а может состоять из объемов закупки разных валют (многомерный). В примере фигурирует только одна величина.

Уровни рядов динамики

Понятие «уровень» относится к интересующим замеренным числам. В расчетной документации в большинстве случаев зашифровываются латинской литерой «y».

Базисный или первый уровень подразумевает начальное число в таблице, конечный – последнее. Все, что связано со временем фиксации факта, скрывается под «t».

Расчеты среднего уровня в рядах динамики

Существуют случаи, когда требуются какие-то резюмирующие значения. Среднее – из таких. При этом методики его определения для разных видов рядов отличаются.

Интервальный ряд динамики

В этом случае требуется просто поиск среднего арифметического. Таким образом можно показать какие-то сезонные колебания производства, продаж.

Рассчитать можно по формуле:

В нашем случае подобная цифирь полезной нагрузки не несет, только для наглядности:

(144,2 + … + 141,9) / 6 = 866,6 / 6 = 142,77.

Таково среднее население за 5 лет.

Моментный ряд динамики

Если разрыв в датах неизменен, то можно записать последовательность в средних значениях. Получим (n – 1) чисел такого вида

После нехитрых выкладок обнаруживаем, что

y(1), y(n) – базисный и конечный уровни;

((141.2 + 141,9) / 2 + 143,5 + … + 142) / 5 = (143,05 + 570,5) / 2 = 142,71.

Мы получили среднее хронологическое.

Но это для равных отрезков. Когда они меняются, необходимо учитывать временной фактор. Если уровни меняются с течением времени, то выводится такое:

Выражение несколько упрощается, если уровни постоянны до следующей отсечки.

t(i) – длительность периода, когда уровень i зафиксирован.

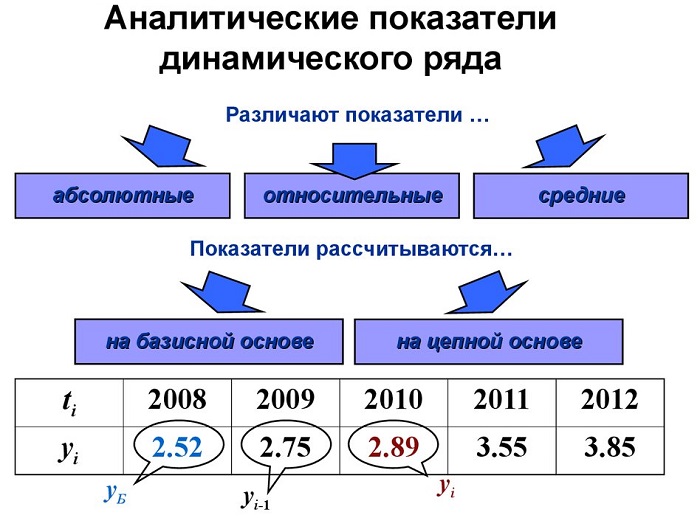
Показатели анализа рядов динамики

Методы анализа сводятся к видоизменению полученных данных к виду, облегчающему отслеживание динамики и выявляющему ее направленность. Так или иначе придется сопоставлять уровни для понимания темпов роста / убыли.

Для оценки применяются абсолютные (вычитание уровней) и относительные (отношение уровней ряда) величины.

Базисные показатели можно получить, если сравнивать с первым элементом. Цепные показатели – с соседними.

Это базисная и цепная абсолютные разницы соответственно.

То же в относительном выражении. В таком виде мы получим характеристику в виде коэффициента. Для более наглядного представления следует умножить на «100» и получить %%.

Надо заметить, что цепные критерии имеют свойства накапливаться и переходить в базисные:

И самые важные для оценки параметров динамики понятия — темпы:

Опять же в абсолютном и относительных видах. Если речь идет об анализе плавной кривой, то отношение заменит производная, указывающая на тангенс угла наклона касательной прямой.

Об усредненных величинах мы уже говорили. Стоит немного вернуться и рассмотреть их в связи с темпами:

Так выглядят базисный и цепной средние темпы прироста:

А вот так в относительных единицах.

Теперь на основании изложенного дополним нашу исходную таблицу и сделаем напрашивающиеся выводы.

Вполне очевидно, что отрицательные значения абсолютных величин и менее 1 относительные указывают на падение населения. При этом темпы роста ниже 0, и это указывает на сохранение неблагоприятной тенденции.

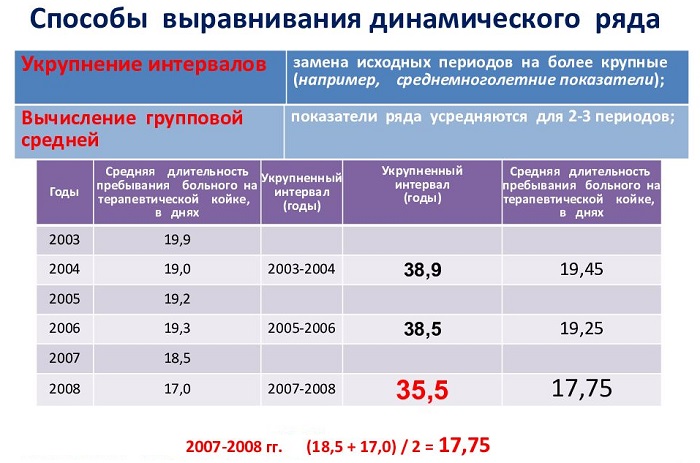
Методы выравнивания рядов динамики

Выравнивание используется для определения общего направления динамики процессов. Кратковременные случайные всплески роста / падения иногда нарушают целостность восприятия картины.

Ещё можно заметить, что:

Увеличение периодов позволяет построить данные таким образом, чтобы изменения явно демонстрировали основную линию. Выравниваются средние значения.

Плавающая средняя означает, что она подсчитывается из определенного числа соседних уровней. По новым правилам построения организуется новый ряд из средних. Метод оптимален, если графическая интерпретация близка к прямой. В противном случае искажение динамики может оказаться чрезмерным.

Аналитический метод сводится к аппроксимации параметров математическим уравнением с высокой корреляцией. Дальнейшая работа базируется на нем. Так легче выявить тенденцию, можно позволить какие-то прогнозы. Облегчается использование численных методов.

Заключение

Ряды динамики позволяют понятными способами анализировать полученные данные. Наглядными становятся происходящие изменения.

Ситуация становится еще более ясной на графиках с представлением средних, различий, темпов роста / падения.

Источник