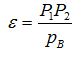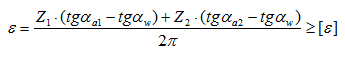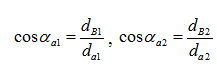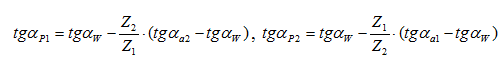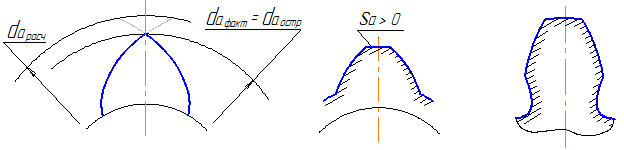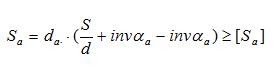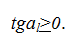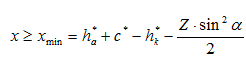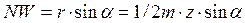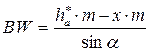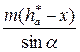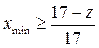что такое интерференция зубьев колеса

2.7. ИНТЕРФЕРЕНЦИЯ ЗУБЧАТЫХ КОЛЕС

Интерференция профилей приводит к заклиниванию зубьев одного колеса во впадинах другого. Для исключения интерференции в эвольвентном зацеплении точки касания профилей зубьев колес должны всегда находиться на линии зацепления, что обеспечивается при угле профиля α = 20° числом зубьев колес больше 17.

При нарезании эвольвентных зубчатых колес с числами зубьев меньше 17 имеет место интерференция части профиля зуба колеса и профилей зубьев режущего инструмента. В этом случае режущие кромки инструмента срезают часть формообразующей кривой профилей зубьев колеса.

При положительных значениях коэффициента относительного смещения имеет место интерференция профилей зубьев режущего инструмента и части эвольвентного профиля, принадлежащего головке зуба колеса, что приводит к срезу этой части профиля. В этом случае имеет место заострение зуба колеса (рис.8).

Изменение профилей зубьев колес приводит к увеличению нагрузочной способности механизма. Заострение головок зубьев зубчатых колес является нежелательным, т. к. это приводит к снижению кинематической точности механизма и вызывает увеличение склонности зубьев к скалыванию.

Рисунок 8. Заострение зуба колеса.

Зуб зубчатого колеса считается незаостренным, а зубчатый механизм − сохраняющим работоспособность при выполнении следующего условия:

где [sa ] − допускаемое значение толщины зуба по окружности вершин sa:

При отрицательных значениях коэффициента относительного смещения относительного, имеет место интерференция профилей зубьев режущего инструмента и части эвольвентного профиля, принадлежащего ножке зуба колеса, что приводит к срезу этой части профиля. В этом случае имеет место подрезание части профиля зуба колеса в его основании в области переходной кривой (рис. 9).

Изменение профилей зубьев колес приводит к увеличению кинематической точности механизма. Подрезание ножек зубьев зубчатых колес является нежелательным, т. к. это ослабляет ножку зуба колеса, что приводит к уменьшению нагрузочной способности механизма.

Зуб зубчатого колеса считается не подрезанным, а зубчатый механизм − сохраняющим работоспособность при выполнении следующего условия:

Минимальное значение коэффициента относительного смещения, при котором обеспечивается отсутствие подреза ножек и заострение головок зубьев зубчатых колес, определяется по выражению

Источник

iSopromat.ru

Геометрические показатели качества зацепления зубчатых колес показывают совокупность линий в системе координат и для определенной передачи представляют собой замкнутый контур, отделяющий разрешенную зону для выбора коэффициентов смещения от запрещенной.

При проектировании зубчатой передачи необходимо проверить геометрические показатели, которые могут привести к неудовлетворительной ее работе.

— коэффициент перекрытия. Коэффициентом перекрытия называется отношение дуги зацепления к шагу зацепления на той же окружности (дуга зацепления – это путь, проходимый точкой зуба по дуге окружности за время работы данной пары – на рисунке 39б показана дуга зацепления по основной окружности – b₁b₂).

Если дуга зацепления окажется меньше шага, то при выходе из зацепления одной пары зубьев следующая не вступит в зацепление. Нарушается преемственность в работе пар, передача работает с ударами и быстро выходит из строя. Поэтому коэффициент перекрытия должен быть больше или, в крайнем случае, равен единице.

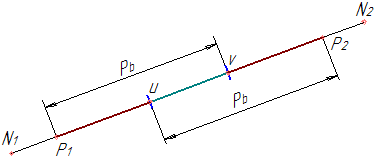
Чем больше коэффициент перекрытия, тем более плавной будет работа передачи. На основании третьего свойства эвольвенты рабочая часть линии зацепления Р₁Р₂ равна дуге зацепления на основной окружности (рисунок 39б), а расстояние между работающими профилями двух соседних зубьев, измеренное по линии зацепления равно основному шагу. Поэтому коэффициент перекрытия можно вычислить как отношение отрезка Р₁Р₂ к основному шагу р_В (рисунок 43):

После преобразований получаем:

В этой формуле α_a1 и α_a2 – углы профиля на окружности вершин первого и второго колеса соответственно. Определяются через функцию косинуса:

Рекомендуется принимать следующие значения допускаемого коэффициента перекрытия:

[ ε ]=1,05…1,1 – для неответственных передач,
[ ε ]=1,2 – для ответственных передач.

При нарезании колес стандартным инструментом реечного типа коэффициент перекрытия в цилиндрической передаче не может превышать значения 1,88. То есть в реальных передачах значения коэффициента перекрытия располагаются в интервале 1,05…1.8. Это означает, что какую-то часть времени работают две пары зубьев одновременно, какую-то – одна пара зубьев.

В тот момент времени, когда пара зубьев входит в зацепление в точке Р₁, предыдущая пара находится от нее на расстоянии основного шага в точке “v” линии зацепления (рисунок 43). С этого момента в зацеплении находятся две пары (и делят передаваемую нагрузку между собой). Когда предыдущая пара подойдет к точке Р₂, то следующая пара будет располагаться в точке» u” (на расстоянии основного шага от точки Р₂).

В следующий момент предыдущая пара выйдет из зацепления, а следующая войдет в зону ”uv” и будет воспринимать всю нагрузку целиком. Пока пара находится в зоне “uv” никакая другая пара находиться в зацеплении не будет. Поэтому эта часть линии зацепления называется зоной однопарного зацепления. Часть профиля, которая работает в зоне однопарного зацепления, является наиболее напряженной частью этого профиля.

Чем больше коэффициент перекрытия, тем меньше зона однопарного зацепления, тем большую часть времени в зацеплении находятся две пары зубьев.

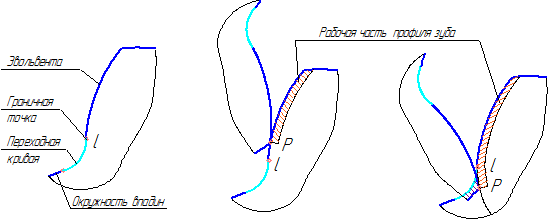
— интерференция зубьев зубчатых колес. Профиль зуба состоит из двух характерных частей – из эвольвентной части, и переходной кривой, плавно сопрягающей эвольвентную часть с окружностью впадин (рисунок 44 а).

Если рабочая часть профиля располагается целиком на его эвольвентной части, то происходит нормальная работа зубьев без нарушения основного закона зацепления (рисунок 44 б). Если же нижняя точка Р рабочего участка окажется ближе к основной окружности, чем граничная точка l сопряжения эвольвенты с переходной кривой, то вершина зуба одного колеса будет стремиться к внедрению в переходную кривую второго (рисунок 44 в).

Положение точки на эвольвенте можно задать через различные параметры (через диаметр, через угол профиля, через угол развернутости, через эвольвентный угол). Наиболее удобные формулы получаются через углы профиля в рассматриваемых точках (формула для определения угла профиля в граничной точке l приведена выше, формулы для определения угла профиля в точках Р₁ и Р₂ получаются из рассмотрения рисунка 39б):

Условие отсутствия интерференции:

При приложении нагрузки к вершине будут возникать большие напряжения (теоретически площадь равна нулю), что приведет к смятию пластичного материала или к разрушению хрупкого материала у этой вершины. Поэтому при проектировании передачи необходимо обеспечить у зуба некоторую толщину на окружности вершин S_a>0 (рисунок 45 б).

При проверке на отсутствие заострения толщина зуба на окружности вершин сравнивается с допускаемой величиной:

Рекомендуется принимать следующие значения допускаемой толщины зуба на окружности вершин:

[S_a]=0,25m – для пластичных материалов;
[S_a]=0,40m – для хрупких материалов;

— подрезание (подрез) зубьев. При определенных условиях инструмент начинает пересекать им же сформированную эвольвенту у основания зуба. Формируемая им переходная кривая в этом случае пересекает эвольвенту изнутри (а не плавно с ней сопрягается), а зуб становится более тонким (ослабленным) у основания. Это явление носит название подрезания или подреза зубьев (рисунок 45в).

Зубья с подрезом можно применять для несиловых передач, если оставшийся участок эвольвенты обеспечивает необходимый коэффициент перекрытия. Для силовых передач применять зубья с подрезом не рекомендуется. При применении стандартного инструмента реечного типа подрез зубьев происходит в том случае, когда верхняя точка прямолинейного участка профиля зуба рейки заходит за точку N линии зацепления (рисунок 41). Поэтому проверка на отсутствие очень простая:

Вероятность подреза повышается с уменьшением числа зубьев колеса. Если изготавливать колеса стандартным инструментом реечного типа без применения смещения, то подрез будет наблюдаться у колес с числом зубьев меньше 17 (Z_min=17), и чем меньше число зубьев, тем более значительным будет подрез. Однако, если правильно подобрать коэффициент смещения, то колесо с любым число зубьев можно нарезать без подреза. Подрез у колеса с заданным числом зубьев будет отсутствовать, если коэффициент смещения будет не меньше минимального:

Влиять на все указанные геометрические показатели качества зацепления можно правильным выбором коэффициентов смещения. Для рационального выбора коэффициентов смещения при проектировании передачи разработаны так называемые блокирующие контуры.

Так как показатели описываются соответствующими математическими зависимостями, то их можно представить в виде линий в определенной системе координат. Совокупность этих линий в системе координат (x₁ – x₂ ) для определенной пары колес (z₁ – z₂) представляет собой замкнутый контур, отделяющий разрешенную зону для выбора коэффициентов смещения (x₁ и x₂) от запрещенной.

Этот замкнутый контур и называется блокирующим контуром. Он позволяет конструктору спроектировать бесчисленное количество работоспособных передач с одинаковыми числами зубьев колес, но с различными свойствами.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

2.7. ИНТЕРФЕРЕНЦИЯ ЗУБЧАТЫХ КОЛЕС

Интерференция профилей приводит к заклиниванию зубьев одного колеса во впадинах другого. Для исключения интерференции в эвольвентном зацеплении точки касания профилей зубьев колес должны всегда находиться на линии зацепления, что обеспечивается при угле профиля α = 20° числом зубьев колес больше 17.

При нарезании эвольвентных зубчатых колес с числами зубьев меньше 17 имеет место интерференция части профиля зуба колеса и профилей зубьев режущего инструмента. В этом случае режущие кромки инструмента срезают часть формообразующей кривой профилей зубьев колеса.

При положительных значениях коэффициента относительного смещения имеет место интерференция профилей зубьев режущего инструмента и части эвольвентного профиля, принадлежащего головке зуба колеса, что приводит к срезу этой части профиля. В этом случае имеет место заострение зуба колеса (рис.8).

Изменение профилей зубьев колес приводит к увеличению нагрузочной способности механизма. Заострение головок зубьев зубчатых колес является нежелательным, т. к. это приводит к снижению кинематической точности механизма и вызывает увеличение склонности зубьев к скалыванию.

Рисунок 8. Заострение зуба колеса.

Зуб зубчатого колеса считается незаостренным, а зубчатый механизм − сохраняющим работоспособность при выполнении следующего условия:

где [sa ] − допускаемое значение толщины зуба по окружности вершин sa:

При отрицательных значениях коэффициента относительного смещения относительного, имеет место интерференция профилей зубьев режущего инструмента и части эвольвентного профиля, принадлежащего ножке зуба колеса, что приводит к срезу этой части профиля. В этом случае имеет место подрезание части профиля зуба колеса в его основании в области переходной кривой (рис. 9).

Изменение профилей зубьев колес приводит к увеличению кинематической точности механизма. Подрезание ножек зубьев зубчатых колес является нежелательным, т. к. это ослабляет ножку зуба колеса, что приводит к уменьшению нагрузочной способности механизма.

Зуб зубчатого колеса считается не подрезанным, а зубчатый механизм − сохраняющим работоспособность при выполнении следующего условия:

Минимальное значение коэффициента относительного смещения, при котором обеспечивается отсутствие подреза ножек и заострение головок зубьев зубчатых колес, определяется по выражению

Рисунок 9. Подрезание зуба колеса.

3. ОПРЕДЕЛЕНИЕ РАЗМЕРОВ ЗУБЧАТОГО ЗАЦЕПЛЕНИЯ

Размеры колес, а также всего зацепления, зависят от чисел Z1 и Z2 зубьев колес, от модуля m зацепления (определяемого из расчета зуба колеса на прочность), общего для обоих колес, а также от метода их обработки.

Предположим, что колеса изготавливаются по методу обкатки инструментом реечного типа (инструментальной рейкой, червячной фрезой), который профилируется на основе исходного контура согласно ГОСТ 13755-81 (рис. 10).

Процесс изготовления зубчатого колеса (рис. 10) инструментальной рейкой по методу обкатки заключается в том, что рейка в движении по отношению к обрабатываемому колесу перекатывается без скольжения одной из своих делительных прямых (ДП) или средней прямой (СП) по делительной окружности колеса (движение обкатки) и одновременно совершает быстрые возвратно-поступательные перемещения вдоль оси колеса, снимая при этом стружку (рабочее движение).

Расстояние между средней прямой рейки (СП) и той делительной прямой (ДП), которая в процессе обкатки перекатывается по делительной окружности колеса, называется смещением Х рейки (см. п. 2.6). Очевидно, что смещение Х равно расстоянию, на которое отодвинута средняя прямая рейки от делительной окружности колеса. Смещение считается положительным, если средняя прямая отодвинута в направлении от центра нарезаемого колеса.

Величина смещения Х определяется формулой:

где х – коэффициент смещения, который имеет положительное или отрицательное значение (см. п. 2.6).

Рисунок 10. Станочное зацепление.

Зубчатые колеса, изготовленные без смещения инструментальной рейки, называются нулевыми; изготовленные при положительном смещении рейки – положительными, при отрицательном смещении – отрицательными.

В зависимости от значений х_Σ зубчатые зацепления классифицируются следующим образом:

а)если х_Σ = 0, при чем х1 = х2 = 0, то зацепление называется нормальным (нулевым);

в)если х_Σ ≠ 0, то зацепление называется неравносмещенным, при чем при х Σ > 0 зацепление называется положительным неравносмещенным, а при х Σ

Применение нормальных зубчатых колес с постоянной высотой головки зубьев и постоянным углом зацепления, вызвано стремлением получить систему сменных зубчатых колес с постоянным расстоянием между центрами для одной и той же суммы чисел зубьев, с одной стороны, и с другой стороны – сократить число комплектов зуборезного инструмента в виде модульных фрез, которыми снабжаются инструментальные мастерские. Однако условие сменности зубчатых колес при постоянном расстоянии между центрами может быть удовлетворено и при применении косозубых колес, а также колесами, нарезанными со смещением инструмента. Наибольшее применение нормальные зубчатые колеса находят в передачах при значительных числах зубьев обоих колес (при Z₁ > 30), когда эффективность применения смещения инструмента значительно меньше.

При равносмещенном зацеплении ( х Σ = х₁ + х₂ = 0) толщина зуба (S₁) по делительной окружности шестерни увеличивается за счет уменьшения толщины зуба (S₂) колеса, но сумма толщин по делительной окружности сцепляющихся зубьев остается постоянной и равной шагу. Таким образом, нет необходимости в раздвигании осей колес; начальные окружности так же, как и у нормальных колес, совпадают с делительными; угол зацепления не изменяется, но меняется соотношение высот головок и ножек зубьев. В связи с тем, что прочность зубьев колеса понижается, такое зацепление может применяться только при малых числах зубьев шестерни и значительных передаточных отношениях.

При неравносмещенном зацеплении ( х Σ = х₁ + х₂ ≠ 0) сумма толщин зубьев по делительным окружностям обычно больше, чем у нулевых колес. Поэтому оси колес приходится раздвигать, начальные окружности не совпадают с делительными и угол зацепления увеличен. Неравносмещенное зацепление имеет большие возможности, чем равносмещенное, и поэтому имеет более широкое распространение.

Применяя смещение инструмента при нарезании зубчатых колес можно повысить качество зубчатого зацепления:

а) устранить подрезание зубьев шестерни при малом числе зубьев;

б) повысить прочность зубьев на изгиб (до 100 %);

в) повысить контактную прочность зубьев (до 20 %);

г) повысить износостойкость зубьев и др.

Но следует иметь в виду, что улучшение одних показателей ведет к ухудшению других.

Существуют простые системы, которые позволяют определить смещение по простейшим эмпирическим формулам. Эти системы повышают показатели работы передач по сравнению с нулевыми, однако они не используют все возможности смещения.

В соответствии с рекомендациями ISO предложены следующие правила выбора коэффициентов смещения:

а) при числе зубьев шестерни Z₁ ≥ 30 применяют нормальные колеса;

Суммарное смещение ограничивается величиной:

в) при числе зубьев шестерни Z₁ суммарном числе зубьев Z₁ + Z₂

Суммарное смещение ограничивается величиной:

х Σ ≤ 1,8 – 0,03 · (Z₁ + Z₂), если 30 х Σ является максимально возможной при выполнении следующих требований:

а) не должно быть подрезания зубьев при обработке их инструментальной рейкой;

б) предельно допустимая толщина зуба по окружности выступов принята 0,3m;

в) наименьшее значение коэффициента перекрытия ε_α = 1,1;

г) обеспечение наибольшей контактной прочности;

д) обеспечение наибольшей прочности на изгиб и равнопрочности (равенства напряжений изгиба) зубьев шестерни и колеса, изготовленных из одинакового материала с учетом разного направления сил трения на зубьях;

е) наибольшей износостойкости и наибольшего сопротивления заданного (равенство удельных скольжений в крайних точках зацепления).

Данными таблицами нужно пользоваться следующим образом:

а) для неравномерного внешнего зацепления коэффициенты смещения х1 и х2 определяются в зависимости от передаточного отношения

i_1,2: при 2 ≥ i_1,2 ≥ 1 по табл. 1; при 5 ≥ i_1,2 > 2 по табл. 2, 3 по заданным Z₁ и Z₂.

После определения коэффициентов смещения все размеры зацепления подсчитываются по формулам, приведенным в табл. 5.

Источник

Подрезание – наложение профиля зуба инструмента на профиль зуба изготавливаемого колеса при нарезании зубьев.

Заклинивание – наложение профилей зубьев, но не при изготовлении, а при зацеплении колес.

Рассмотрим подробней явление подрезания. Так как параметры зуборезного инструмента стандартны, то при прочих равных условиях возможность подрезания ножки зуба определяется положением точки N, т.е. размерами колеса. Подрезание не происходит, когда точка контакта между производящей поверхностью инструмента и профилем зуба нарезаемого колеса находится правее точки N. Левее точки N эти поверхности будут не касаться друг друга, а пересекаться, что и приводит к подрезанию ножки зуба. Подрезание уменьшает эвольвентную часть профиля зуба колеса, ослабляет прочность зуба в опасном сечении и уменьшает коэффициент перекрытия.

Рассмотрим вопрос о наименьшем числе зубьев Z_min на колесе, при котором явление подрезания будут отсутствовать при нарезании зубьев рейкой с учетом смещения.

По условию не подрезания, должно выполняться условие NW ≥ BW. Из треугольника ОNW можно выразить катет NW, используя модуль и число зубьев

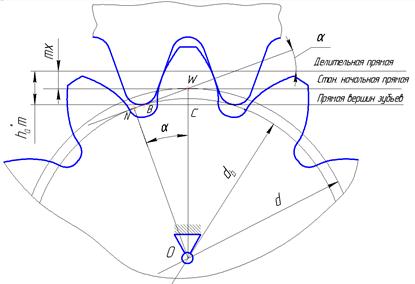
Из треугольника BWC можно найти гипотенузу BW, используя модуль,

высоту головки зуба и коэффициент смещения Рисунок 5 инструмента

≥

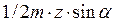
Отсюда число зубьев, которое можно нарезать реечным инструментом без подрезания ножки зуба, с учётом смещения будет равно

= (3)

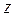
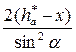
Минимальное число зубьев без смещения реечного инструмента и без подрезания ножки зуба, можно нарезать

==17,01 (4)

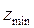
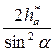
Используя выражение (3) и (4), можно определить минимальный коэффициент смещения, при котором не будет подрезания ножки зуба.

Смещение зуборезного инструмента меняет не только параметры зубчатых колес, но и зацепления в целом, поэтому при исправлении смещением, рассматривается суммарный коэффициент смещения (х_å).

В последних двух случаях такое исправление называется угловым.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

3. ОПРЕДЕЛЕНИЕ РАЗМЕРОВ ЗУБЧАТОГО ЗАЦЕПЛЕНИЯ

Размеры колес, а также всего зацепления, зависят от чисел Z1 и Z2 зубьев колес, от модуля m зацепления (определяемого из расчета зуба колеса на прочность), общего для обоих колес, а также от метода их обработки.

Предположим, что колеса изготавливаются по методу обкатки инструментом реечного типа (инструментальной рейкой, червячной фрезой), который профилируется на основе исходного контура согласно ГОСТ 13755-81 (рис. 10).

Процесс изготовления зубчатого колеса (рис. 10) инструментальной рейкой по методу обкатки заключается в том, что рейка в движении по отношению к обрабатываемому колесу перекатывается без скольжения одной из своих делительных прямых (ДП) или средней прямой (СП) по делительной окружности колеса (движение обкатки) и одновременно совершает быстрые возвратно-поступательные перемещения вдоль оси колеса, снимая при этом стружку (рабочее движение).

Расстояние между средней прямой рейки (СП) и той делительной прямой (ДП), которая в процессе обкатки перекатывается по делительной окружности колеса, называется смещением Х рейки (см. п. 2.6). Очевидно, что смещение Х равно расстоянию, на которое отодвинута средняя прямая рейки от делительной окружности колеса. Смещение считается положительным, если средняя прямая отодвинута в направлении от центра нарезаемого колеса.

Величина смещения Х определяется формулой:

где х – коэффициент смещения, который имеет положительное или отрицательное значение (см. п. 2.6).

Рисунок 10. Станочное зацепление.

Зубчатые колеса, изготовленные без смещения инструментальной рейки, называются нулевыми; изготовленные при положительном смещении рейки – положительными, при отрицательном смещении – отрицательными.

В зависимости от значений х_Σ зубчатые зацепления классифицируются следующим образом:

а)если х_Σ = 0, при чем х1 = х2 = 0, то зацепление называется нормальным (нулевым);

в)если х_Σ ≠ 0, то зацепление называется неравносмещенным, при чем при х Σ > 0 зацепление называется положительным неравносмещенным, а при х Σ

Применение нормальных зубчатых колес с постоянной высотой головки зубьев и постоянным углом зацепления, вызвано стремлением получить систему сменных зубчатых колес с постоянным расстоянием между центрами для одной и той же суммы чисел зубьев, с одной стороны, и с другой стороны – сократить число комплектов зуборезного инструмента в виде модульных фрез, которыми снабжаются инструментальные мастерские. Однако условие сменности зубчатых колес при постоянном расстоянии между центрами может быть удовлетворено и при применении косозубых колес, а также колесами, нарезанными со смещением инструмента. Наибольшее применение нормальные зубчатые колеса находят в передачах при значительных числах зубьев обоих колес (при Z₁ > 30), когда эффективность применения смещения инструмента значительно меньше.

При равносмещенном зацеплении ( х Σ = х₁ + х₂ = 0) толщина зуба (S₁) по делительной окружности шестерни увеличивается за счет уменьшения толщины зуба (S₂) колеса, но сумма толщин по делительной окружности сцепляющихся зубьев остается постоянной и равной шагу. Таким образом, нет необходимости в раздвигании осей колес; начальные окружности так же, как и у нормальных колес, совпадают с делительными; угол зацепления не изменяется, но меняется соотношение высот головок и ножек зубьев. В связи с тем, что прочность зубьев колеса понижается, такое зацепление может применяться только при малых числах зубьев шестерни и значительных передаточных отношениях.

При неравносмещенном зацеплении ( х Σ = х₁ + х₂ ≠ 0) сумма толщин зубьев по делительным окружностям обычно больше, чем у нулевых колес. Поэтому оси колес приходится раздвигать, начальные окружности не совпадают с делительными и угол зацепления увеличен. Неравносмещенное зацепление имеет большие возможности, чем равносмещенное, и поэтому имеет более широкое распространение.

Применяя смещение инструмента при нарезании зубчатых колес можно повысить качество зубчатого зацепления:

а) устранить подрезание зубьев шестерни при малом числе зубьев;

б) повысить прочность зубьев на изгиб (до 100 %);

в) повысить контактную прочность зубьев (до 20 %);

г) повысить износостойкость зубьев и др.

Но следует иметь в виду, что улучшение одних показателей ведет к ухудшению других.

Существуют простые системы, которые позволяют определить смещение по простейшим эмпирическим формулам. Эти системы повышают показатели работы передач по сравнению с нулевыми, однако они не используют все возможности смещения.

В соответствии с рекомендациями ISO предложены следующие правила выбора коэффициентов смещения:

а) при числе зубьев шестерни Z₁ ≥ 30 применяют нормальные колеса;

Суммарное смещение ограничивается величиной:

в) при числе зубьев шестерни Z₁ суммарном числе зубьев Z₁ + Z₂

Суммарное смещение ограничивается величиной:

х Σ ≤ 1,8 – 0,03 · (Z₁ + Z₂), если 30 х Σ является максимально возможной при выполнении следующих требований:

а) не должно быть подрезания зубьев при обработке их инструментальной рейкой;

б) предельно допустимая толщина зуба по окружности выступов принята 0,3m;

в) наименьшее значение коэффициента перекрытия ε_α = 1,1;

г) обеспечение наибольшей контактной прочности;

д) обеспечение наибольшей прочности на изгиб и равнопрочности (равенства напряжений изгиба) зубьев шестерни и колеса, изготовленных из одинакового материала с учетом разного направления сил трения на зубьях;

е) наибольшей износостойкости и наибольшего сопротивления заданного (равенство удельных скольжений в крайних точках зацепления).

Данными таблицами нужно пользоваться следующим образом:

а) для неравномерного внешнего зацепления коэффициенты смещения х1 и х2 определяются в зависимости от передаточного отношения

i_1,2: при 2 ≥ i_1,2 ≥ 1 по табл. 1; при 5 ≥ i_1,2 > 2 по табл. 2, 3 по заданным Z₁ и Z₂.

После определения коэффициентов смещения все размеры зацепления подсчитываются по формулам, приведенным в табл. 5.

Источник