что такое интегрируемая функция
ИНТЕГРИРУЕМАЯ ФУНКЦИЯ
Смотреть что такое «ИНТЕГРИРУЕМАЯ ФУНКЦИЯ» в других словарях:
АБСОЛЮТНО ИНТЕГРИРУЕМАЯ ФУНКЦИЯ — функция, у к рой интегрируема ее абсолютная величина. Если функция интегрируема по Риману на отрезке то ее абсолютная величина интегрируема по Риману на этом отрезке и Аналогичное утверждение справедливо для функции ппеременных, интегрируемой по… … Математическая энциклопедия
ЛОКАЛЬНО ИНТЕГРИРУЕМАЯ ФУНКЦИЯ — в точке М функция, интегрируемая в том или ином смысле в нек рой окрестности точки М. Если действительная функция f, определенная на отрезке [ а, b], есть точная конечная производная функции F, действительной и определенной на том же отрезке, то… … Математическая энциклопедия
ФУНКЦИЙ ТЕОРИЯ — раздел математики, занимающийся изучением свойств различных функций. Теория функций распадается на две области: теорию функций действительного переменного и теорию функций комплексного переменного, различие между которыми настолько велико, что… … Энциклопедия Кольера
Теорема Лебега о мажорируемой сходимости — У этого термина существуют и другие значения, см. Теорема Лебега. Теорема Лебега о мажорируемой сходимости в функциональном анализе, теории вероятностей и смежных дисциплинах это теорема, утверждающая, что если сходящаяся почти всюду… … Википедия
ДВОЙСТВЕННОСТЬ — 1) Д. в алгебраической геометрии двойственность между различными пространствами когомологий на алгебраич. многообразиях. Когомологий когерентных пучков. Пусть X неособое проективное алгебраич. многообразие размерности nнад алгебраически замкнутым … Математическая энциклопедия
ЗНАКИ МАТЕМАТИЧЕСКИЕ — условные обозначения, предназначенные для записи математич. понятий и выкладок. Напр., понятие квадратный корень из числа, равного отношению длины окружности к ее диаметру обозначается кратко а предложение отношение длины окружности к ее диаметру … Математическая энциклопедия
Теорема Ньютона — Лейбница — Формула Ньютона Лейбница или теорема анализа даёт соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной. Если непрерывна на отрезке и ее любая первообразная на этом отрезке, то и … Википедия
Теорема Ньютона — Формула Ньютона Лейбница или основная теорема анализа даёт соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной. Если непрерывна на отрезке и ее любая первообразная на этом отрезке, то имеет … Википедия
ЛИНЕЙНОЕ ЭЛЛИПТИЧЕСКОЕ УРАВНЕНИЕ И СИСТЕМА — дифференциальное уравнение (и система) с частными производными вида где L линейный эллиптич. оператор Оператор (1) с действительными коэффициентами эллиптичен в точке х, если характеристич. форма является определенной в этой точке. Здесь… … Математическая энциклопедия
Определенный интеграл Римана, Дарбу, Ньютона-Лейбница, виды интегрируемых функций
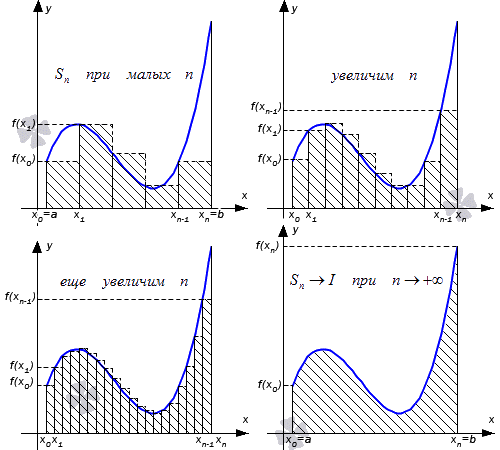
После обобщения выражения и определения получили, что любая непрерывная функция y = f ( x ) с числом I имеет отрезок, который и получил название определенного интеграла.
Его геометрическое понятие было показано в школе в 11 классе. Рассмотрим рисунок, приведенный ниже. Имеем изображение определенного интеграла.
В данной статье будет показано определения определенного интеграла, которые были заданы Риманом и Дарбу, Ньютоном-Лейбницом. Подробно будет показано условие интегрируемости функции на заданном определенном отрезке с перечислением интегрируемых функций.
Определенный интеграл Римана
Рассмотрим рисунок, приведенный ниже.
Числа a и b называют нижним и верхним пределом интегрирования, а f ( x ) – подынтегральная функция, где x – переменная интегрирования.
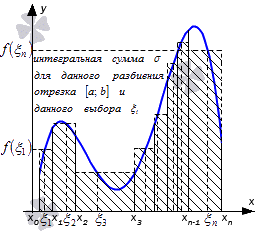
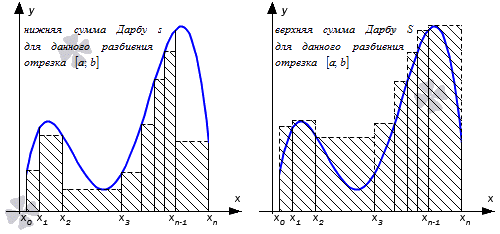
Определенный интеграл Дарбу
Чтобы понять необходимо и достаточное условие существования определенного интеграла Дарбу, необходимо применить несколько определений.
для разбиения отрезка [ a ; b ] называют нижней и верхней суммами Дарбу.
Рассмотрим рисунок, приведенный ниже.
Определенный интеграл Ньютона-Лейбница
Рассмотрим подробно понятие определенного интеграла Ньютона-Лейбница.
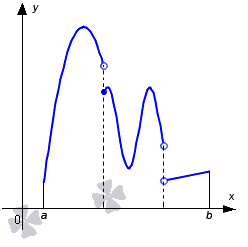
Необходимое условие интегрируемости функции на отрезке, виды интегрируемых функций
Рассмотрим необходимое условие существования определенного интеграла функции на отрезке.
Виды функций, для которых существует определенный интеграл:
Рассмотрим рисунок, приведенный ниже. На нем располагается пример интегрируемой функции.
Итоги
Задавание определенного интеграла Римана происходит через предел интегральных сумм, а интеграл Дарбу – предел разности верхних и нижних сумм Дарбу, в свою очередь интеграл Ньютона-Лейбница – при помощи значения первообразной.
Интегралы для чайников: как решать, правила вычисления, объяснение
Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл. Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?
Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Изучаем понятие « интеграл »
Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц, но суть вещей не изменилась.
Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о пределах и производных, необходимые и для понимания интегралов, уже есть у нас в блоге.
Неопределенный интеграл
Пусть у нас есть какая-то функция f(x).
Неопределенным интегралом функции f(x) называется такая функция F(x), производная которой равна функции f(x).
Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как вычислять производные, читайте в нашей статье.
Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.
Простой пример:
Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.
Полная таблица интегралов для студентов
Определенный интеграл
Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.
В качестве примера представим себе график какой-нибудь функции.
Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:
Точки а и b называются пределами интегрирования.
Бари Алибасов и группа
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Правила вычисления интегралов для чайников
Свойства неопределенного интеграла
Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.
Свойства определенного интеграла
Как считать определенный интеграл? С помощью формулы Ньютона-Лейбница.
Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:
Примеры решения интегралов
Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.
Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Интегрирующая функция
Эвристическая функция
Существо эвристической функции состоит в содействии приросту научных знаний, в том числе в создании предпосылок для научных открытий. Философский метод, применяемый в единстве с формально-логическим, обеспечивает приращение знаний, конечно, в собственно философской сфере.
Координирующая функция философии.
Существо этой функции состоит в координировании методов в процессе научного исследования. На первый взгляд она кажется излишней: если метод содержателен, обусловлен природой объекта, то какая-либо дополнительная координация методов, помимо их координации предметом познания, представляется ненужной и даже вредной. Исследователю достаточно ориентироваться на сам объект, на соответствие метода этому объекту, чтобы иметь важную предпосылку результативного научного поиска. В общем виде данное рассуждение верно.
Интегрирующая функция.
Термин «интеграция» (от латинского integratio — восстановление, восполнение) означает объединение в целое каких-либо частей. Он применяется во многих науках и практике, и уже утвердился в статусе общенаучного понятия: некоторые из философов полагают, что по своей всеобщности это понятие приблизилось к классу философских категорий.
Применительно к функциям философии термин «интегрирующий» связан с представлением об объединяющей роли философского знания по отношению к какому-либо множеству элементов, составляющих систему или способных образовать целостность.
На уровне науки в целом философия выступает в качестве одного из необходимых факторов интеграции научного знания.
Логико-гносеологическая функция.
Эта функция заключается в разработке самого философского метода, его нормативных принципов, а также в логико-гносеологическом обосновании тех или иных понятийных и теоретических структур научного знания.
Выработка информации, необходимой для совершенствования элементов всеобщего метода, сочетается с применением ее для развития общенаучных методов познания, например, системного подхода, метода моделирования. Будучи примененными к построению научных теорий, принципы диалектики как логики включаются в состав их логических (или гносеологических) оснований.
4. Уровни философского знания
Философия имеет ряд аспектов. Прежде всего, ее интересуют проблемы бытия:
Что такое сущее и имеет ли смысл, существующий мир?
Можно ли, изучая человека, выйти на тайны бытия?
Раскрываются ли в человеке истоки существования?
Философское учение о человеке, получившее широкое развитие в последние годы, некоторым философами-марксистами рассматривается как философская дисциплина, отвечающая на вопрос «Что такое человек?», синтезирующая объективно-научное и ценностное видение человека и мира.
АБСОЛЮТНО ИНТЕГРИРУЕМАЯ ФУНКЦИЯ
функция, у к-рой интегрируема ее абсолютная величина. Если функция 
интегрируема по Риману на отрезке 
то ее абсолютная величина интегрируема по Риману на этом отрезке и
В случае несобственных одномерных интегралов в смысле Римана или Лебега по промежутку 
(при условии, что функция f(x) интегрируема по Риману или, соответственно, по Лебегу на любом отрезке 
) из существования несобственного интеграла от абсолютной величины функции
следует и существование интеграла
но не наоборот (см. Абсолютно сходящийся несобственный интеграл). При этом, если существует несобственный интеграл
то функция f(х).интегрируема по Лебегу на промежутке [ а, b).и несобственный интеграл от нее равен интегралу Лебега.
В случае функций многих переменных (число к-рых n>1) несобственные интегралы обычно определяются таким образом, что существование несобственного интеграла от абсолютной величины функции равносильно существованию несобственного интеграла от самой функции.
Пусть значения функции 
принадлежат нек-рому банахову пространству с нормой 
Тогда функция 
наз. абсолютно интегрируемой на измеримом множестве Е, если существует интеграл
при этом, если функция 
интегрируема на Е, то
Лит.:[1] Ильин В. А., Позняк 9. Г., Основы математического анализа, ч. 1, 3 изд., М., 1971; [2] Кудрявцев Л. Д., Математический анализ, т. 1, 2 изд., М., 1973; [3]Никольский С. М., Курс математического анализа, 2 изд., т. 1, М., 1975; [4] Шварц Л., Анализ, пер. с франц., т. 1, М., 1972. Л.
Полезное
Смотреть что такое «АБСОЛЮТНО ИНТЕГРИРУЕМАЯ ФУНКЦИЯ» в других словарях:
ФУНКЦИЙ ТЕОРИЯ — раздел математики, занимающийся изучением свойств различных функций. Теория функций распадается на две области: теорию функций действительного переменного и теорию функций комплексного переменного, различие между которыми настолько велико, что… … Энциклопедия Кольера
ДВОЙСТВЕННОСТЬ — 1) Д. в алгебраической геометрии двойственность между различными пространствами когомологий на алгебраич. многообразиях. Когомологий когерентных пучков. Пусть X неособое проективное алгебраич. многообразие размерности nнад алгебраически замкнутым … Математическая энциклопедия
Интеграл — (от лат. integer целый) одно из важнейших понятий математики, возникшее в связи с потребностью, с одной стороны, отыскивать функции по их производным (например, находить функцию, выражающую путь, пройденный движущейся точкой, по скорости… … Большая советская энциклопедия
ЭРГОДИЧЕСКАЯ ТЕОРИЯ — Введение Э. т. (метрическая теория динамических систем) раздел теории динамических систем, изучающий их статистич. свойства. Возникновение Э. т. (1 я треть 20 в.) было стимулировано попытками доказать эргодическую гипотезу (термин введён П. и Т.… … Физическая энциклопедия
Условное математическое ожидание — В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете … Википедия