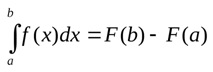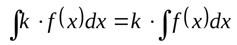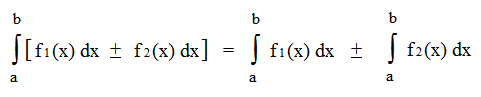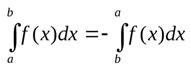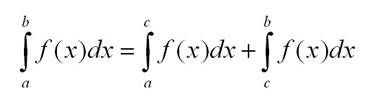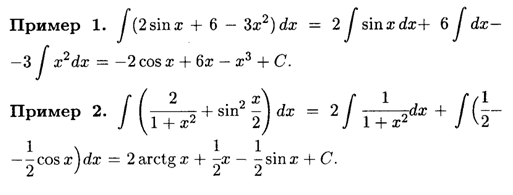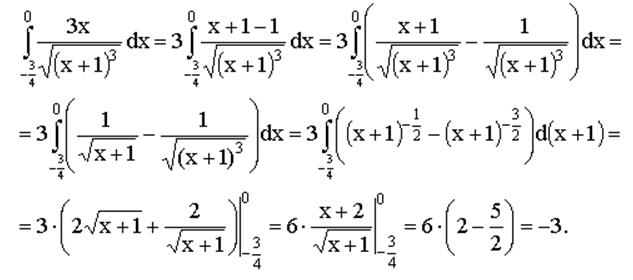что такое интеграл видео
Интегралы – что это, как решать, примеры решений и объяснение для чайников
За 4 минуты вы узнаете, что такое интегрирование. Как интеграл связан с производными. Чем отличается определенный интеграл от неопределенного. 5 примеров вычисления интегралов
Почему вы не знаете, как решать интегралы
А для чего нужны интегралы? Попробуйте сами себе ответить на этот вопрос.
Объясняя тему интегралов, учителя перечисляют малополезные школьным умам области применения. Среди них:
Связать все эти процессы не всегда получается, поэтому многие ученики путаются, даже при наличии всех базовых знаний для понимания интеграла.
Главная причина незнания – отсутствие понимания практической значимости интегралов.
Нужна помощь в написании работы?
Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.
Интеграл – что это?
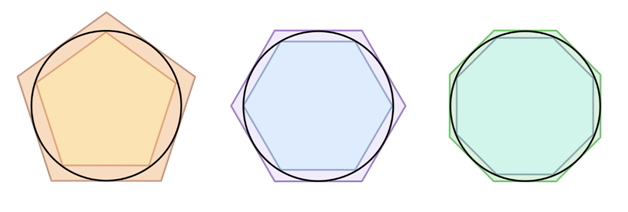
Предпосылки. Потребность в интегрировании возникла в Древней Греции. В то время Архимед начал применять для нахождения площади окружности методы, похожие по сути на современные интегральные исчисления. Основным подходом для определения площади неровных фигур тогда был «Метод исчерпывания», который достаточно лёгок для понимания.
Суть метода. В данную фигуру вписывается монотонная последовательность других фигур, а затем вычисляется предел последовательности их площадей. Этот предел и принимался за площадь данной фигуры.
Метод исчерпывания для определения площади круга
В этом методе легко прослеживается идея интегрального исчисления, которая заключается в нахождении предела бесконечной суммы. В дальнейшем эта идея применялась учёными для решения прикладных задач астронавтики, экономики, механики и др.
Современный интеграл. Классическая теория интегрирования была сформулирована в общем виде Ньютоном и Лейбницем. Она опиралась на существовавшие тогда законы дифференциального исчисления. Для её понимания, необходимо иметь некоторые базовые знания, которые помогут математическим языком описать визуальные и интуитивные представления об интегралах.
Объясняем понятие «Интеграл»
Процесс нахождения производной называется дифференцированием, а нахождение первообразной – интегрированием.
Интеграл математическим языком – это первообразная функции (то, что было до производной) + константа «C».
Интеграл простыми словами – это площадь криволинейной фигуры. Неопределенный интеграл – вся площадь. Определенный интеграл – площадь в заданном участке.
Интеграл записывается так:
Каждая подынтегральная функция умножается на компонент «dx». Он показывает, по какой переменной осуществляется интегрирование. «dx» – это приращение аргумента. Вместо X может быть любой другой аргумент, например t (время).
Неопределённый интеграл
Неопределенный интеграл не имеет границ интегрирования.
Для решения неопределённых интегралов достаточно найти первообразную подынтегральной функции и прибавить к ней «C».
Определённый интеграл
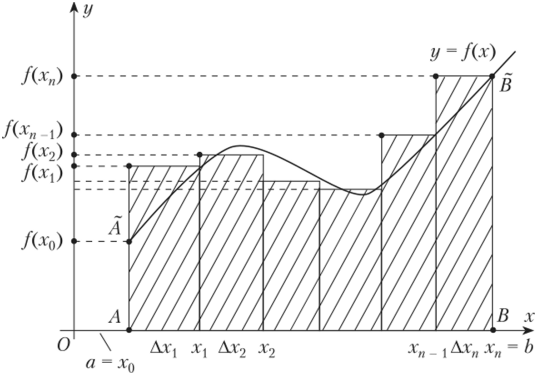
В определенном интеграле на знаке интегрирования пишут ограничения «a» и «b». Они указаны на оси X в графике ниже.
Точки A и B на оси X – есть ограничение зоны определения интеграла
Для вычисления определенного интеграла необходимо найти первообразную, подставить в неё значения «a» и «b» и найти разность. В математике это называется формулой Ньютона-Лейбница:
Таблица интегралов для студентов (основные формулы)
Скачайте формулы интегралов, они вам еще пригодятся
Как вычислять интеграл правильно
Существует несколько простейших операций для преобразования интегралов. Вот основные из них:
Вынесение константы из-под знака интеграла
Разложение интеграла суммы на сумму интегралов
Если поменять местами a и b, знак изменится
Можно разбить интеграл на промежутки следующим образом
Это простейшие свойства, на основе которых потом будут формулироваться более сложные теоремы и методы исчисления.
Примеры вычисления интегралов
Решение неопределенного интеграла
Решение определенного интеграла
Базовые понятия для понимания темы
Чтобы вы поняли суть интегрирования и не закрыли страницу от непонимания, мы объясним ряд базовых понятий. Что такое функция, производная, предел и первообразная.
Функция – правило, по которому все элементы из одного множества соотносятся со всеми элементами из другого.
Производная – функция, описывающая скорость изменения другой функции в каждой конкретной точке. Если говорить строгим языком, – это предел отношения приращения функции к приращению аргумента. Он вычисляется вручную, но проще использовать таблицу производных, в которой собрано большинство стандартных функций.
Приращение – количественное изменение функции при некотором изменении аргумента.
Предел – величина, к которой стремиться значение функции, при стремлении аргумента к определённому значению.
Пример предела: допустим при X равном 1, Y будет равно 2. Но что, если X не равен 1, а стремится к 1, то есть никогда её не достигает? В этом случае y никогда не достигнет 2, а будет только стремиться к этой величине. На математическом языке это записывается так: limY(X), при X –> 1 = 2. Читается: предел функции Y(X), при x стремящемся к 1, равен 2.
Как уже было сказано, производная – это функция, описывающая другую функцию. Изначальная функция может быть производной для какой-либо другой функции. Эта другая функция называется первообразной.
Заключение
Найти интегралы не трудно. Если вы не поняли, как это делать, прочитайте статью еще раз. Со второго раза становится понятнее. Запомните! Решение интегралов сводится к простым преобразованиям подынтегральной функции и поиска её в таблице интегралов.
Если текстовое объяснение вам не заходит, посмотрите видео о смысле интеграла и производной:
Интегралы для чайников: как решать, правила вычисления, объяснение
Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл. Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?
Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Изучаем понятие « интеграл »
Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц, но суть вещей не изменилась.
Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о пределах и производных, необходимые и для понимания интегралов, уже есть у нас в блоге.
Неопределенный интеграл
Пусть у нас есть какая-то функция f(x).
Неопределенным интегралом функции f(x) называется такая функция F(x), производная которой равна функции f(x).
Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как вычислять производные, читайте в нашей статье.
Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.
Простой пример:
Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.
Полная таблица интегралов для студентов
Определенный интеграл
Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.
В качестве примера представим себе график какой-нибудь функции.
Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:

Точки а и b называются пределами интегрирования.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Правила вычисления интегралов для чайников
Свойства неопределенного интеграла
Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.
Свойства определенного интеграла
Как считать определенный интеграл? С помощью формулы Ньютона-Лейбница.
Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:
Примеры решения интегралов
Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.
Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Интегралы
Метод замены переменной при решении неопределенных интегралов
В этом видео уроке рассказывается о том, как использовать метод замены переменной при решении неопределенных интегралов. В первой части обучения будет рассмотрена схема применения данного метода. Метод замены переменной является основным методом решения неопределенных интегралов. Его еще часто называют методом подстановки. После изучения теоретической части, полученные знания будут применяться на практических заданиях. С этой целью, в данном видео уроке представлено решение нескольких примеров.
Простейшие интегралы. Решение с помощью таблицы
Определенный интеграл (11 класс). Понятие, решение примера
Что такое интеграл
Решение интегралов с квадратичной функцией, примеры
Видео «Решение интегралов с квадратичной функцией, примеры» посвящено вопросу о том, как правильно выполнять интегрирование выражений, в состав которых входит квадратичная функция. Здесь дается алгоритм вычисления интеграла, который начинается с выделения полного квадрата квадратичной функции. Затем выполняется замена переменной. Полученный упрощенный интеграл решается обычным способом. После того как интеграл вычислен, остается вернуться к первоначальным переменным. Кроме теоретического.
Интегралы с бесконечными пределами (несобственные 1 рода)
Видео «Интегралы с бесконечными пределами (несобственные 1 рода)» посвящено вопросу о том, что такое интегралы с бесконечными пределами и каков их геометрический смысл, решение примера. Допустим, что задан определенный интеграл от непрерывной функции с верхним пределом интегрирования равным B. Представим себе, что значение этого интеграла численно равно площади криволинейной трапеции. При увеличении значения предела B, площадь этой трапеции также увеличивается. Возникает вопрос, к какому.
Как найти объем тела вращения через вычисление определенного интеграла
Как найти длину дуги кривой через вычисление определенного интеграла
Онлайн урок «Как найти длину дуги кривой через вычисление определенного интеграла» посвящен вопросу о методе, с помощью которого можно определить длину дуги кривой. Одним из приложений определенного интеграла является нахождение длин дуг кривых. Здесь будет представлена формула, с помощью которой можно найти длину дуги кривой. Для решения данной задачи с помощью этой формулы необходимо знать функцию, которой задана кривая и абсциссы точек, между которыми измеряется длина кривой. В данном видео.
Это видео посвящено вопросу о том, как использовать метод интегрирования по частям при решении определенного интеграла, формула, пример использования. Если вы уже освоили данный метод при решении неопределенных интегралов, то вам не составит труда научиться его использовать и для вычисления определенного интеграла. Также необходимо уметь применять формулу Ньютона-Лейбница. Здесь представлена формула, по которой будет проводиться вычисление интеграла. Применение метода интегрирования по частям.
Интегралы
Что такое интеграл
Формула Ньютона-Лейбница, примеры с решением определенного интеграла
Универсальная тригонометрическая подстановка, пример решения интеграла
В этом видео рассказывается о том, как решаются интегралы при помощи универсальной тригонометрической подстановки. Данный метод можно использовать для вычисления некоторых интегралов, содержащих тригонометрические функции в подынтегральном выражении. В первой части урока вам будет представлена общая схема решения таких интегралов. После теоретической части, разобранный алгоритм действий будет применен при решении конкретного задания. С этой целью в данном видео уроке приведен пример, в котором.
Решение неопределенных интегралов, свойства, примеры
Это видео посвящено вопросу о том, как правильно производить вычисление интегралов. Здесь вы ознакомитесь с некоторыми свойствами неопределенного интеграла, которые часто используются при его решении. Это свойство линейности и первообразной функции. Для удобства решения интегралов будет представлена таблица интегралов. Такие таблицы помогают решать некоторые примеры. В этом онлайн уроке рассматриваются примеры вычисления интегралов с использованием данной таблицы и изученных свойств. В одном.
Решение интегралов с квадратичной функцией, примеры
Видео «Решение интегралов с квадратичной функцией, примеры» посвящено вопросу о том, как правильно выполнять интегрирование выражений, в состав которых входит квадратичная функция. Здесь дается алгоритм вычисления интеграла, который начинается с выделения полного квадрата квадратичной функции. Затем выполняется замена переменной. Полученный упрощенный интеграл решается обычным способом. После того как интеграл вычислен, остается вернуться к первоначальным переменным. Кроме теоретического.
Простейшие интегралы. Решение с помощью таблицы
Определенный интеграл (11 класс). Понятие, решение примера
Это видео посвящено вопросу о том, как использовать метод интегрирования по частям при решении определенного интеграла, формула, пример использования. Если вы уже освоили данный метод при решении неопределенных интегралов, то вам не составит труда научиться его использовать и для вычисления определенного интеграла. Также необходимо уметь применять формулу Ньютона-Лейбница. Здесь представлена формула, по которой будет проводиться вычисление интеграла. Применение метода интегрирования по частям.
Метод замены переменной при решении определенного интеграла, примеры
В этом онлайн уроке рассказывается о том, как применять метод замены переменной при вычислении определенного интеграла с примером решения. Если вы разобрались использованием метода замены переменной при решении неопределенного интеграла, то вам не составит труда научиться использовать его и при решении определенного интеграла, ведь сама схема метода замены переменной при этом существенно не меняется. Здесь будет рассмотрен весь порядок действий данного метода с подробным объяснением. Кроме.
Интегралы
Метод замены переменной при решении определенного интеграла, примеры
В этом онлайн уроке рассказывается о том, как применять метод замены переменной при вычислении определенного интеграла с примером решения. Если вы разобрались использованием метода замены переменной при решении неопределенного интеграла, то вам не составит труда научиться использовать его и при решении определенного интеграла, ведь сама схема метода замены переменной при этом существенно не меняется. Здесь будет рассмотрен весь порядок действий данного метода с подробным объяснением. Кроме.
Формула Ньютона-Лейбница, примеры с решением определенного интеграла
Интегрирование иррациональных функций, пример с решением интеграла
Здесь рассказывается о том, как выполняется интегрирование иррациональных функций. Рассматриваемый интеграл имеет запись подынтегральной функции, которая указывает на то, что над выражениями, являющимися аргументами функции, производятся только рациональные операции. Таким образом, интеграл может содержать переменную x, а также одинаковые дробно-линейные выражения, которые возводятся в различные рациональные степени. По этой причине рассматриваемая подынтегральная функция является.
Универсальная тригонометрическая подстановка, пример решения интеграла
В этом видео рассказывается о том, как решаются интегралы при помощи универсальной тригонометрической подстановки. Данный метод можно использовать для вычисления некоторых интегралов, содержащих тригонометрические функции в подынтегральном выражении. В первой части урока вам будет представлена общая схема решения таких интегралов. После теоретической части, разобранный алгоритм действий будет применен при решении конкретного задания. С этой целью в данном видео уроке приведен пример, в котором.
Интегрирование тригонометрических функций, примеры решений
Урок «Интегрирование тригонометрических функций, примеры решений» посвящен вопросу о том, как решать интегралы с тригонометрическими выражениями. Порядок проводимых действий при решении таких интегралов может отличаться в зависимости от самого тригонометрического выражения. Здесь рассматриваются различные варианты таких выражений и алгоритмы действий, которые необходимо выполнять при интегрировании той или иной функции. В этом видео уроке помимо теоретической части присутствует и практические.
Интегрирование рациональных дробей с примером решения
В этом онлайн уроке рассказывается о том, как правильно выполняется интегрирование рациональных дробей с примером решения. Если подынтегральная функция является рациональной дробью, т.е. отношение двух многочленов, то для решения данного интеграла необходимо воспользоваться следующим алгоритмом. Если речь идет о неправильной рациональной дроби, то её необходимо представить в виде суммы целой части многочлена и правильной рациональной дроби. Затем нужно разложить правильную рациональную дробь на.
Решение неопределенных интегралов, свойства, примеры
Это видео посвящено вопросу о том, как правильно производить вычисление интегралов. Здесь вы ознакомитесь с некоторыми свойствами неопределенного интеграла, которые часто используются при его решении. Это свойство линейности и первообразной функции. Для удобства решения интегралов будет представлена таблица интегралов. Такие таблицы помогают решать некоторые примеры. В этом онлайн уроке рассматриваются примеры вычисления интегралов с использованием данной таблицы и изученных свойств. В одном.