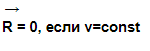что такое инерциальная система отсчета в физике
Инерциальные системы отсчета.
Инерциальными системами отсчета называют такие системы, относительно которых все тела, не испытывающие действия сил, движутся равномерно и прямолинейно.
Если какая-либо система отсчета движется относительно инерциальной системы поступательно, но не прямолинейно и равномерно, а с ускорением или же вращаясь, то такая система не может быть инерциальной и закон инерции в ней не выполняется.
Во всех инерциальных системах отсчета все механические и физические процессы протекают совершенно одинаково (при одинаковых условиях).
Согласно принципу относительности, все инерциальные системы отсчета равноправны и все проявления законов физики в них выглядят одинаково, а записи этих законов в разных инерциальных системах отсчета имеют одинаковую форму.
Если в изотропном пространстве существует хотя бы одна инерциальная система отсчета, приходим к выводу, что существует бесконечное множество таких систем, движущихся друг относительно друга поступательно, равномерно и прямолинейно. Если инерциальные системы отсчета существуют, то пространство однородно и изотропно, а время – однородно.
Законы Ньютона и другие законы динамики выполняются только в инерциальных системах отсчета.
Рассмотрим пример инерциальной и неинерциальной систем. Возьмем тележку, на которой находятся два шарика. Один из них лежит на горизонтальной поверхности, а другой подвешен на нити. Сначала тележка движется относительно Земли прямолинейно и равномерно (а). Силы, действующие на каждый шарик по вертикали, уравновешены, а по горизонтали на шарики никакие силы не действуют (силу сопротивления воздуха можно проигнорировать).
При любой скорости движения тележки относительно земли (υ1, υ2, υ3 и т.д.) шарики будут находиться в покое относительно тележки, главное, чтобы скорость была постоянной.
Однако, когда тележка наедет на песчаную насыпь (б), ее скорость начнет быстро уменьшаться, в результате чего тележка остановится. Во время торможения тележки оба шарика придут в движение – изменят свою скорость относительно тележки, хотя их никакие силы не толкают.
В этом примере первой (условно неподвижной) системой отсчета является Земля. Вторая система отсчета, движущаяся относительно первой – тележка. Пока тележка двигалась равномерно и прямолинейно, шарики находились в покое относительно тележки, т. е. выполнялся закон инерции. Как только тележка стала тормозить, т. е. начала двигаться с ускорением относительно инерциальной (первой) системы отсчета, закон инерции перестал выполняться.
Строго инерциальной системы отсчета нет. Реальная система отсчета всегда связывается с каким-нибудь конкретным телом, по отношению к которому изучается различных объектов. Все реальные тела движутся с каким-либо ускорением, следовательно любая реальная система отсчета может рассматриваться в качестве инерциальной лишь приближенно.
Инерциальной системой с очень высокой степенью точности считается гелиоцентрическая система, связанная с центром Солнца и координатными осями, направленными на три далекие звезды. Эту систему используют в задачах небесной механики и космонавтики. В большинстве технических задач инерциальной системой отсчета считают любую систему, жестко связанную с землей (или любым телом, которое покоится или движется прямолинейно и равномерно относительно поверхности Земли).
Инерция
Понятие инерция в формулировках Галилея и Ньютона
Галилео Галилей и Исаак Ньютон внесли свой вклад в развитие такого раздела физики, как механика. Неудивительно, что каждый из них предложил свою формулировку.
Галилео Галилей
Исаак Ньютон
Формулировка закона инерции
Когда тело движется по горизонтальной поверхности, не встречая никакого сопротивления движению, то его движение — равномерно, и продолжалось бы постоянно, если бы плоскость простиралась в пространстве без конца.
Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не принуждается приложенными силами изменить это состояние.
Инерция — это физическое явление, при котором тело сохраняет свою скорость постоянной или покоится, если на него не действуют другие тела.
Инерция – это физическое явление сохранения скорости тела постоянной, если на него не действуют другие тела или их действие скомпенсировано.
Варианты формулировки не противоречат друг другу и говорят по сути об одном и том же, просто разными словами — выбирайте ту, что вам нравится больше.
Сила: первый закон Ньютона
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причина любого действия или взаимодействия — сила.
Сила — это физическая векторная величина, которая воздействует на данное тело со стороны других тел. Она измеряется в Ньютонах (в честь Исаака Ньютона, разумеется).
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.
Теперь зная, что такое сила, мы можем вернуться к ньютоновской формулировке закона инерции — он же, Его Величество, первый закон Ньютона:
Существуют такие системы отсчета, относительно которых тело сохраняет свою скорость постоянной, в том числе равной нулю, если действие на него других сил отсутствует или скомпенсировано.
Первый закон Ньютона
R — результирующая сила, сумма всех сил, действующих на тело [Н]
const — постоянная величина
В этом законе встречается такое словосочетание, как «система отсчета». Оно изучается в самом начале курса физики, но там это понятие читают в контексте «такие системы отсчета». Напрашивается вопрос: какие такие системы отсчета?
Системы отсчета: инерциальные и неинерциальные
Чтобы описать движение нам нужны три штуки:
В совокупности эти три опции образуют систему отсчета:
Инерциальная система отсчета — система отсчёта, в которой все тела движутся прямолинейно и равномерно, либо покоятся.
Неинерциальная система отсчета — система отсчёта, движущаяся с ускорением.
Рассмотрим разницу между этими системами отсчета на примере задачи.
Аэростат — летательный аппарат на картиночке ниже — движется равномерно и прямолинейно параллельно горизонтальной дороге, по которой равноускоренно движется автомобиль.
Выберите правильное утверждение:
Решение:
Система отсчёта, связанная с землёй, инерциальна. Да, планета движется и вращается, но для всех процессов вблизи планеты этим можно пренебречь. Во всех задачах систему отсчета, связанную с землей можно считать инерциальной.
Поскольку система отсчёта, связанная с землёй инерциальна, любая другая система, которая движется относительно земли равномерно и прямолинейно или покоится — по первому закону Ньютона тоже инерциальна.
Движение аэростата удовлетворяет этому условию, так как оно равномерное и прямолинейное, а равноускоренное движение автомобиля — нет. Аэростат — инерциальная система отсчёта, а автомобиль — неинерциальная.
Ответ: 1.
Инерция покоя
На столе лежит лист бумаги. На него поставили стакан и резко выдернули лист бумаги из-под него. Стакан почти не двинулся.
То, что стакан остался в состоянии покоя, можно объяснить законом инерции, так как «скорость остается постоянной, в том числе равной нулю». В данном случае инерция покоя — это способность тела сохранять состояние полного механического покоя и «сопротивляться» любым внешним воздействиям. То есть та часть закона инерции, в котором скорость равна нулю.
Так, например, если выбивать пыль из ковра, то в ковер-самолет ваш любимый предмет интерьера не превратится — вместе с пылью не улетит.
Инерция движения
В случае с движением мы берем ту часть первого закона Ньютона, в которой скорость постоянна, но не равна нулю. Здесь мы откроем способность тела к движению, которое было вызвано силой, прекратившей своё действие на тело.
Вернемся к самому началу:
Велосипедист наезжает на камень и падает с велосипеда. Благодаря инерции скорость велосипедиста сохраняется, несмотря на то, что сам велосипед не едет дальше.
Наездник слетает с лошади, если та остановилась. Это тоже происходит из-за инерции — скорость наездника остается постоянной, при этом сама лошадь останавливается.
Мир не идеален
К сожалению, а может быть и к счастью, мы не живем в мире, в котором все тела движутся прямолинейно и равномерно. Из-за этого инерция в реальной жизни невозможна, потому что всегда есть трение, сопротивление воздуха и прочие, препятствующие движению, факторы.
Пуля, вылетевшая из ружья, продолжала бы двигаться, сохраняя свою скорость, если бы на неё не действовало другое тело — воздух. Поэтому скорость пули уменьшается.
Велосипедист, перестав работать педалями, смог бы сохранить скорость своего движения, если бы на велосипед не действовало трение. Поэтому, если педали не крутить — скорость велосипедиста уменьшается, и он останавливается.
Инерциальная система отсчёта
Инерциальной называется система отсчёта, по отношению к которой пространство является однородным и изотропным, а время — однородным.
Содержание
Свойства инерциальных систем отсчёта
Всякая система отсчёта, движущаяся относительно ИСО равномерно и прямолинейно, также является ИСО. Согласно принципу относительности, все ИСО равноправны, и все законы физики инвариантны относительно перехода из одной ИСО в другую. Это значит, что проявления законов физики в них выглядят одинаково, и записи этих законов имеют одинаковую форму в разных ИСО.
Предположение о существовании хотя бы одной ИСО в изотропном пространстве приводит к выводу о существовании бесконечного множества таких систем, движущихся друг относительно друга со всевозможными постоянными скоростями. Если ИСО существуют, то пространство будет однородным и изотропным, а время — однородным; согласно теореме Нётер, однородность пространства относительно сдвигов даст закон сохранения импульса, изотропность приведёт к сохранению момента импульса, а однородность времени — к сохранению энергии движущегося тела.
Если скорости относительного движения ИСО, реализуемых действительными телами, могут принимать любые значения, связь между координатами и моментами времени любого «события» в разных ИСО осуществляется преобразованиями Галилея.
В специальной теории относительности скорости относительного движения ИСО, реализуемых действительными телами, не могут превышать некоторой конечной скорости «C» (скорость распространения света в вакууме) и связь между координатами и моментами времени любого «события» в разных ИСО осуществляется преобразованиями Лоренца.
Связь с реальными системами отсчёта
С разной степенью точности и в зависимости от области использования инерциальными системами можно считать системы отсчёта, связанные с: Землёй, Солнцем, неподвижные относительно звезд.
Геоцентрическая инерциальная система координат
Применение Земли в качестве ИСО, несмотря на приближённый его характер, широко распространено в навигации. Инерциальная система координат, как часть ИСО строится по следующему алгоритму. В качестве точки O- начала координат выбирается центр земли в соответствии с принятой её моделью. Ось z – совпадает с осью вращения земли. Оси x и y находятся в экваториальной плоскости. Следует заметить, что такая система не участвует во вращении Земли.
Удивительное об инерциальных системах
Первая редакция опубликована на сайте
http://zhurnal.lib.ru/z/zhmudx_w_a/systems.shtml
Инерциальными системами названы системы, в которых тело может оставаться в покое или двигаться равномерно прямолинейно сколь угодно долго в отсутствии сторонних сил. Возможность и необходимость такого движения здесь тождественны. Казалось бы, всё просто и понятно с младых ногтей.
Однако:
Обращает на себя внимание отсутствие в природе подобных систем.
Мы сами не находимся в инерциальной системе. Система, связанная с поверхностью Земли, инерционной не является, поскольку поверхность Земли вращается, а вся Земля движется вокруг Солнца. Даже в ограниченном пространстве маятник Фуко позволяет выявить отличия этой системы от инерциальной. Проявление сил Кориолиса и отклонение маятника Фуко выявляют вращательное движение тела. Мы допускаем существование такой системы, в которой бы проявления этих сил не было, и такую систему можно было бы назвать условно инерциальной.
Обращение вокруг Солнца не выявляется этими экспериментами в замкнутом пространстве вблизи поверхности Земли. Поэтому, кажется, нет оснований для отторжения подобной системы от определения «инерциальной», вопреки тому факту, что такая система отнюдь не покоится, а движется, причем не прямолинейно, а, следовательно, и не равномерно, и даже не равноускоренно (вектор ускорения меняется). Мы не ставим вопроса, должна ли такая система характеризоваться полным отсутствием вращения относительно системы, связанной с Солнцем, или же она должна вращаться таким образом, чтобы одна и та же точка постоянно была направлена на Солнце. Видимо, именно вторая система не будет отличаться от инерциальной системы в опытах в замкнутом пространстве с маятником Фуко.
Итак, вращение астрономического объекта вносит определенные сложности, и можем отметить, что существует, по-видимому, одна и только одна система, связанная с этим объектом, которая наиболее близко отвечает понятию инерциальной для экспериментов вблизи поверхности этого объекта, но всё-таки не тождественна инерциальной системе.
Примеры с шайбой на льду убедительны только на малых расстояниях и малых временах.
На больших расстояниях, где искривление Земли было бы заметным, траектория шайбы должна повторять это искривление. Шайба не будет двигаться «равномерно и прямолинейно» сколь угодно долго по той простой причине, что она не движется «равномерно и прямолинейно» и на малых интервалах. Просто НА МАЛЫХ ИНТЕРВАЛАХ ЭТО НЕ ЗАМЕТНО.
Отклонение от прямолинейной траектории лежит в пределах метрологической чувствительности метода. Но чисто теоретически если шайба движется прямолинейно вблизи планеты, то расстояние до центра масс меняется, следовательно, сила притяжения также меняется. Если ледяная опора обеспечивает в этих условиях прямолинейность движения, то будет меняться скорость движения тела. Если же лед повторяет по форме сферу и тело движется перпендикулярно силе притяжения, то меняется направление движения этого тела. Итак, ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ НЕ МОЖЕТ БЫТЬ РЕАЛИЗОВАНО ВБЛИЗИ ПОВЕРХНОСТИ ЗЕМЛИ, поскольку нет требуемой ситуации с отсутствием сторонних сил.
Если бы мы вышли в космос, то наличие астрономических объектов все равно обеспечит действие сил притяжения с некоторой равнодействующей ненулевой силой.
Если мы ищем инерциальные системы без предварительного ограничения пространства и времени, в котором эта задача решается, то МЫ НАТАЛКИВАЕМСЯ НА НЕПРЕОДОЛИМОЕ ПРОТИВОРЕЧИЕ.
Не только ни одна система не является инерциальной, но и если нам удалось найти некоторую приблизительно инерциальную систему, то система, которая движется относительно неё равномерно и прямолинейно УЖЕ СОВЕРШЕННО ТОЧНО ИНЕРЦИАЛЬНОЙ ВОВСЕ НЕ ЯВЛЯЕТСЯ.
Если бы физики всегда помнили бы об этом! Тогда не было бы попыток из опыта Майкельсона конструировать теоретические положения, распространяющиеся в область космологии, теории возникновения и развития вселенной, футурологии и других наук, занимающихся ЭКСТРАПОЛЯЦИЕЙ!
Получается, что МЫ ДОЛЖНЫ ВВОДИТЬ ОПРЕДЕЛЕНИЕ «ИНЕРЦИАЛЬНАЯ СИСТЕМА ДЛЯ КРАТКОВРЕМЕННО ПРОИЗВОДИМЫХ ОПЫТОВ»?
Проблема не только в этом. Мне могут возразить: «Какое нам дело до того, что в примере со спутником не удается считать его длительно инерциальным объектом? Зачем обсуждать, что это искусственное пространство замкнуто само на себя? Мы можем рассмотреть систему, связанную с Солнцем, и этой проблемы не будет!»
Но загвоздка-то как раз в том и состоит, что эта проблема будет и в том случае, если мы будем рассматривать систему, связанную с Солнцем.
РАССМОТРЕННАЯ ПРОБЛЕМА НЕ ПРЕОДОЛИМА В ПРИНЦИПЕ.
Наблюдение 3. Рассмотрение поведения объектов в системе НА БОЛЬШИХ РАССТОЯНИЯХ вынуждает переходить к более глобальной системе, в которой предыдущая система уже не оказывается инерциальной.
Поскольку при больших скоростях объекты могут достигать больших расстояний за малые времена, следствием Наблюдения 3 будет следующее наблюдение:
Наблюдение 4. Рассмотрение поведения объектов в системе при больших скоростях ВЫНУЖДАЕТ ПЕРЕХОДИТЬ К БОЛЕЕ ГЛОБАЛЬНОЙ СИСТЕМЕ, в которой ПРЕДЫДУЩАЯ СИСТЕМА УЖЕ НЕ ОКАЗЫВАЕТСЯ ИНЕРЦИАЛЬНОЙ.
Наблюдение 5. ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ, сделанные в системе, ограниченной по размерам, времени и скорости, НЕ ПОЗВОЛЯЮТ ДЕЛАТЬ ОБОБЩЕНИЯ по отношению к системам в целом.
Это так важно, что я прошу вас перечитать сказанную фразу ещё раз. При этом речь идет о том, что если хотя бы только размеры, только время или только скорости в системе ограничены, то экспериментальных данных уже только поэтому не достаточно для того, чтобы делать прогнозы в область неограниченного значение по этому же параметру.
Итак, для того, чтобы системы была инерциальной, надо ограничить эту систему во вращательных движениях, во времени и в пространстве и по скорости.
Однако все те же эффекты имеют место и на малых пространственно-временных интервалах, только не так просто выявляются, как на больших. Поэтому критерием применимости понятия инерциальной системы может являться допустимая погрешность от этого приближения.
Инерциальная система без ограничения времени и пространства СУЩЕСТВУЕТ ТОЛЬКО В ВООБРАЖЕНИИ, если из мира изъять все астрономические объекты.
Однако в отсутствие тел ТАКАЯ СИСТЕМА НЕ ПРЕДСТАВЛЯЕТ ИНТЕРЕСА, а при их наличии оставшиеся тела будут играть роль астрономических объектов, поскольку на фоне прочих сил силы притяжения или отталкивания между ними станут играть решающую роль в их траекториях, следовательно, одни из объектов станут двигаться в полях тяготения или отталкивания других.
Утверждение 1. В рамках задачи ближних траекторий в ограниченное время с ограниченной точностью системы, движущиеся только под действием гравитационных сил, проявляют себя как инерциальные (кроме рассмотрения электромагнитных и световых полей).
Доказательство. Все тела получают ускорения, которые не зависят от их массы, поскольку оно пропорционально силе и обратно пропорционально массе, но силы пропорциональны массе. Следовательно, разности ускорений этих тел равны нулю, а их относительные скорости, которые равны интегралу от этих величин, равны некоторым константам, которые не меняются во времени.
Рассмотренное утверждение справедливо по отношению к механике движений под действием гравитационных сил. Мы не обсуждали электромагнетизм и свет. Однако с оговоркой о ближних траекториях в ограниченное время с ограниченной скоростью и в рамках ограниченной точности это утверждение совершенно справедливо и для электромагнитных явлений, и для света. СПРАВЕДЛИВОСТЬ этого для света БЫЛА ПОКАЗАНА в опыте Майкельсона. Но мы видели, что результаты опытов в ограниченном пространстве, времени и скорости НЕЛЬЗЯ РАСШИРИТЕЛЬНО ТРАКТОВАТЬ В ОБЛАСТЬ ГЛОБАЛЬНЫХ ЯВЛЕНИЙ.
В рамках сказанных ограничений и опыт с маятником Фуко не выявит вращения Земли. Мы достоверно знаем, что вращение Земли выявляется экспериментально, но также достоверно знаем, что в реальных условиях оно сказывается слабо.
Можно предположить, что и отклонение света от прямолинейной траектории в движущейся под действием гравитационных сил системе сказывается принципиально, но не выявляется практически.
Прошу внимательно прочитать вышесказанный абзац еще раз.
Речь не идет об отклонении света вследствие гравитации. Речь идет о том, что тело, движущееся лишь под действием гравитации, может в первом приближении считаться находящимся в инерциальной системе отсчета. В первом приближении вблизи этого тела свет распространяется прямолинейно, но этого нельзя утверждать путем экстраполяции этой системы в пространстве, или во времени, или и в пространстве и времени.
Настоятельно необходимо решение вопроса о том, движутся ли равномерно и прямолинейно волновые фронты электромагнитных (и, в частности, световых) полей в системах, охарактеризованных в Утверждении 1?
Мы показали, что ЭТО УТВЕРЖДЕНИЕ НЕ ОБОСНОВАНО ЭКСПЕРИМЕНТАЛЬНО.
Нет никаких экспериментальных оснований для утверждения, что все инерциальные системы одинаково ведут себя по отношению к траектории и скорости света.
Нет никаких экспериментальных оснований для утверждения, что траектория и скорость света одинаково ведет себя во всех инерциальных системах.
Вообще нет никаких данных относительно поведения инерциальных систем отсчета на протяженном времени и (или) в протяженном пространстве.
Можно предположить, что существует, по крайней мере, одна система ДЛЯ КАЖДОЙ ЗАДАЧИ, в которой требование к системе быть «инерциальной» приближенно выполняется, т.е. с достаточной точностью для получения удовлетворительной точности полученного в этом предположении решения задачи.
Эту систему имеет смысл назвать ОСНОВНОЙ. При переходе к более глобальной системе, то есть увеличении точности, времени и пространства задачи, сохранения этого свойства за указанной основной системой не обязательно, но и не отвергается: это будет объектом дальнейшего рассмотрения. Однако, в рамках ограниченной задачи ХОТЯ БЫ ОДНА ТАКАЯ СИСТЕМА, КАК ПРАВИЛО, ЛЕГКО ВЫЯВЛЯЕТСЯ, а именно: это система, которая покоится.
Внимательное рассмотрение теоретических и экспериментальных основ современной физики показывает, что аргументы ПРОТИВ этого принципа весьма НЕУБЕДИТЕЛЬНЫ, основаны на неверных заключениях, иными словами, ошибочны.
Аргументы ЗА сохранение этого принципа остаются довольно СИЛЬНЫМИ.
Отличие поведения траектории световых волн от траектории тела имеют, практически, такую же природу, как отличия траектории движения луча света от космического спутника от траектории самого спутника. В обоих случаях переход к более глобальной системе снимает все противоречия, и тот факт, что глобальная система не глобальна фундаментально, а также остается лишь «относительно инерционной», не меняет сути дела. Обращение Земли вокруг Солнца дает основания указать систему отсчета, связанную с Солнцем, более отвечающей определению «инерциальная», но мы не нуждаемся в такой системе при расчете траекторий бильярдных шаров. Если же нас заинтересует траектория света, отраженного от этих шаров на временном интервале, соизмеримым с календарем, мы без этой системы не обойдемся. Таким образом, рамки решаемой задачи диктуют, что принять за инерциальную систему отсчета, и такую трактовку использует в тои или иной степени любой ученый.
Маятник Фуко ВЫЯВЛЯЕТ вращательное движение. Если теперь сделать такую систему, в которой маятник Фуко сохранял бы направления своих колебаний при любых начальных отклонениях, эта система была бы неотличима от инерциальной в рамках сколь угодно длительных экспериментов в замкнутом пространстве вблизи поверхности Земли. Нет оснований считать эту новую систему не инерциальной в ограниченном пространстве, и нет оснований считать инерциальной старую систему, которая вращается относительно этой новой. Однако опыт Майкельсона был проделан именно в старой, не инерциальной системе.
Еще раз – внимательно: ОПЫТ МАЙКЕЛЬСОНА БЫЛ ПРОДЕЛАН ИМЕННО В НЕ ИНЕРЦИАЛЬНОЙ СИСТЕМЕ. В этой системе СУЩЕСТВУЕТ ВОЗМОЖНОСТЬ ИЗНУТРИ НЕЕ ОПРЕДЕЛИТЬ ЕЕ ДВИЖЕНИЕ, и ОТЛИЧИТЬ ЕГО О ПОКОЯ.
На основании этого опыта Альберт Эйнштейн сделал вывод: НЕ СУЩЕСТВУЕТ ВОЗМОЖНОСТИ ИЗНУТРИ ИНЕРЦИАЛЬНОЙ СИСТЕМЫ ОПРЕДЕЛИТЬ ЕЕ ДВИЖЕНИЕ, и ОТЛИЧИТЬ ЕГО О ПОКОЯ.
Если с опытом Майкельсона что-то не ладно, из этого НЕ СЛЕДУЕТ, что ничего не получится ни с каким другим опытом.
И все же именно такой СТРАННЫЙ ВЫВОД сделал Эйнштейн из данного опыта.
Наблюдение 6. Опыт Майкельсона не только не позволил выявить отличия движущейся инерциальной системы от покоящейся, как это утверждается. Опыт Майкельсона не позволил выявить отличие инерциальной системы от такой системы, которая отличается от инерциальной системы настолько сильно, что это отличие ЛЕГКО ВЫЯВЛЯЕТСЯ ДРУГИМ ОПЫТОМ.
Следовательно, ИЗ ОПЫТА МАЙКЕЛЬСОНА НЕЛЬЗЯ ВЫВОДИТЬ ОБЩИЕ СВОЙСТВА ИНЕРЦИАЛЬНЫХ СИСТЕМ. Но из этого опыта можно делать выводы об общих свойствах систем вообще, и не только инерциальных, но движущихся с ограниченными скоростями в ограниченном пространстве.
Разумеется, что из опыта Майкельсона никак не может следовать, что он проделан в инерциальной системе, если мы знаем, что эта система существенно НЕ ИНЕРЦИАЛЬНАЯ ДЛЯ ЭТОГО КЛАССА ОПЫТОВ. И если МЫ ЗНАЕМ, что в инерциальной системе скорость объектов сохраняется неизменной, то мы, таким образом, знаем, что скорость тех же объектов НЕ МОЖЕТ ОСТАВАТЬСЯ НЕИЗМЕННОЙ В СИСТЕМЕ, КОТОРАЯ НЕ ЯВЛЯЕТСЯ ИНЕРЦИАЛЬНОЙ. А если скорость объектов меняется, а эксперимент не может этого выявить, то из этого с необходимостью следует, что РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТА ИНВАРИАНТНЫ К ТАКИМ ИЗМЕНЕНИЯМ СКОРОСТИ ОБЪЕКТОВ.
Может ли это быть? Ведь в опыте Майкельсона измерялась скорость света!
Ответ на этот вопрос прост для всякого, кто следил за ходом мысли или самостоятельно проследовал по аналогичному пути. Опыт Майкельсона ОШИБОЧНО трактуют как опыт, позволяющий измерить изменения скорости света. Действительно, в этом опыте скорость света НЕ ИЗМЕРЯЕТСЯ, как и в любом другом опыте с аналогичными задачами. Опыт Майкельсона позволяет фиксировать приращения ФАЗОВОГО НАБЕГА СВЕТОВОЙ ВОЛНЫ НА ЗАМКНУТОМ ОТРЕЗКЕ ПУТИ, при условии, что этот отрезок пути поддерживается неизменным В БАЗИСЕ ТВЕРДЫХ ТЕЛ, образующих экспериментальную установку. Результаты эксперимента не исключают возможности того, что СКОРОСТЬ СВЕТА ВО ВСТРЕЧНЫХ НАПРАВЛЕНИЯХ МЕНЯЮТСЯ, они лишь указывают на то, что в этом случае СУММАРНЫЙ СДВИГ ФАЗ ОСТАЕТСЯ НЕИЗМЕННЫМ в масштабе реальных физических объектов.
Еще раз: В МАСШТАБЕ РЕАЛЬНЫХ ФИЗИЧЕСКИХ ОБЪЕКТОВ.
Результаты этого эксперимента также не исключают, что истинная длина оптического пути при этом меняется, однако при этом обнаружено, что данный метод этих изменений не выявляет. Таким образом, гипотеза о том, что масштабы твердых тел меняются по такой же зависимости, что и эффективный оптический путь по замкнутой траектории, вполне согласуется с результатами опыта Майкельсона.
Предположение о том, что скорость света не меняется во всех направлениях в рамках опыта Майкельсона, со всей очевидностью НЕ ОБОСНОВАНО: данная система не является инерциальной в указанных рамках эксперимента.
Итак, ВЫВОД О ПОСТОЯНСТВЕ СКОРОСТИ СВЕТА В ИНЕРЦИАЛЬНЫХ СИСТЕМАХ ОТСЧЕТА НЕ ОБОСНОВАН. Вывод о постоянстве соотношения длины оптического пути по замкнутой траектории и длины этого же пути в метрическом базисе твердых тел, очевидно, может быть сделан не только относительно инерциальных систем, но и с некоторой точностью относительно некоторых неинерциальных систем, таких, как система, связанная с поверхностью Земли.
Здесь не столь важно, соответствует или нет гипотеза о постоянстве скорости света истинному положению вещей, поскольку в данном контексте этот вопрос не может быть решен. Гораздо важнее, что эта гипотеза не следует из данного эксперимента.
ГЕОМЕТРИЧЕСКИЕ РАЗМЕРЫ ФИЗИЧЕСКИХ ТЕЛ ПРИ ДВИЖЕНИИ СИСТЕМЫ В ЭФИРЕ ИЗМЕНЯЮТСЯ ПРОПОРЦИОНАЛЬНО ТОМУ, КАК ИЗМЕНЯЮТСЯ ОПТИЧЕСКАЯ ДЛИНА СВЕТОВОГО ПУТИ ПО ЗАМКНУТОЙ ТРАЕКТОРИИ, ОБРАЗОВАННОЙ ТАКИМИ ФИЗИЧЕСКИМИ ТЕЛАМИ.
ЭТОТ ФАКТ УСТАНОВЛЕН ЭКСПЕРИМЕНТАЛЬНО ОПЫТОМ МАЙКЕЛЬСОНА.
Скорость света в вакууме НЕ ПОСТОЯННА во всех инерциальных системах, поскольку такой вывод не следует из опыта Майкельсона, так как в этом опыте: 1) СВЕТ ДВИГАЛСЯ НЕ В ВАКУУМЕ; 2) СИСТЕМА НЕ БЫЛА ИНЕРЦИАЬНОЙ, 3) СКОРОСТЬ СВЕТА НЕ ИЗМЕРЯЛАСЬ И НЕ СРАВНИВАЛАСЬ С ЧЕМ БЫ ТО НИ БЫЛО.
ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ, которые для виду оправдываются опытом Майкельсона НИ КОИМ ОБРАЗОМ НЕ СЛЕДУЮТ ИЗ ОПЫТА МАЙКЕЛЬСОНА.
Так, например, наблюдая кошку, питающуюся сырой печенкой, невозможно сделать логический вывод: «Муравьи питаются грибами». Такой вывод никак не следует из данного наблюдения.
И даже если какая-то кошка ни с того ни с сего начнет питаться морковкой, данный метод умозаключения ошибочен.
Наблюдая кошку, что бы она там ни ела, нельзя делать выводы о том, что ест муравей, что бы он там ни ел.
Эксперимент с кошкой пополняет наши знания о повадках кошки, но не о муравьях.
Наблюдая не инерциальную систему и движение света в воздухе, недопустимо делать умозаключения об инерциальных системах и вакууме, делая вид, что это одно и то же.
Наблюдая эксперимент с устройством, нечувствительным к изменению частоты света, а следовательно, к фазе, а следовательно, к фазовой скорости – а именно таковым является интерферометр с нулевой разностью хода – нельзя (ВРЕДНО И ОПАСНО ДЛЯ НАУКИ) делать выводы о скорости света. Ибо скорость света в данном наблюдении не измеряется, и не влияет на результат наблюдения по своей природе вхождения в результат.