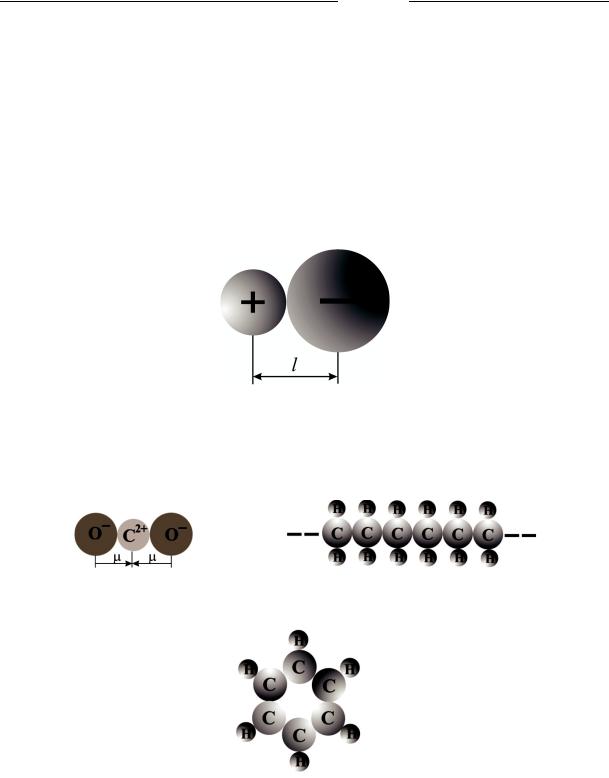что такое индуцированный дипольный момент
Что такое индуцированный дипольный момент
μинд – индуцированный (наведенный) диполь;
μпост – индуцирующий постоянный диполь;
α – поляризуемость молекулы;
Е – напряженность электрического поля.
Диполь-дипольным взаимодействием называется взаимодействие диполей, приводящие к их взаимной ориентации и притяжению. Энергия взаимодействия двух диполей пропорциональна произведению их дипольных моментов.
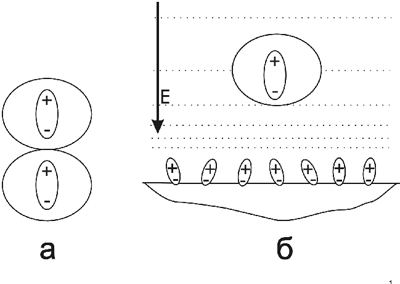
Рисунок 2.1. Диполь-дипольное взаимодействие двух частиц (а) и диполь-полевое взаимодействие полярного адсорбата с поверхностью динамически модифицированного полярного адсорбента (б).
В жидкостной хроматографии, как правило, рассматривается взаимодействие дипольного момента адсорбата с дипольными моментами полярных групп адсорбента; таким образом, диполь-дипольное взаимодействие является одной из причин удерживания молекул, обладающих дипольным моментом, на полярных неподвижных фазах в неполярных средах.
Наиболее характерный случай диполь-дипольного взаимодействия в жидкостной хроматографии соответствует ситуации, когда поверхность полярной неподвижной фазы модифицирована адсорбционным слоем полярного компонента подвижной фазы. Для этого случая моделью однородно модифицированной поверхности неподвижной фазы является эквипотенциальная поверхность, характеризующаяся некоторым усредненным значением напряженности электрического поля (рисунок 2.1.б). Энергия взаимодействия диполя адсорбата с электрическим полем неподвижной фазы равна произведению дипольного момента на напряженность электрического поля:
Напряженность электрического поля полярной адсорбционно модифицированной неподвижной фазы составляет величину порядка 10 9 В/м, а энергия «диполь-полевого» взаимодействия – порядка кДж/моль.
Большая Энциклопедия Нефти и Газа
Индуцированный дипольный момент
Из механизма образования индуцированного дипольного момента молекулы [ см. § 17 ] следует, что его направление совпадает с направлением напряженности электрического поля. [17]
Из результатов исследований можно вычислить индуцированный дипольный момент и соответственно электрическую поляризуемость, которая является количественной мерой деформации двойного слоя. Если па заряженные частицы накладывается переменное неоднородное поле подходящей частоты, электрофоретическая подвижность выпадает и остаются только диэлектрофоретическая и диполофоретическая составляющие. Следует ожидать, что в случае сильно удлиненных коллоидных частиц ( длиной порядка десятых микрона и больше) будет преобладать диполофоретическая слагаемая. [22]
Влияние неоднородности поля волны на индуцированный дипольный момент молекулы с макроскопической точки зрения означает, что поляризованность среды Р ( г) в каждой точке зависит от значения напряженности Е ( г) не только в той же точке г, но и в соседних точках области порядка молекулярных размеров. Другими словами, связь между Р и Е имеет нелокальный характер. То же самое относится, очевидно, и к связи между вектором индукции D и напряженностью Е поля. [23]
Поляризуемость ротатора а определяется как отношение индуцированного дипольного момента к напряженности внешнего поля. [26]
Этот эффект очень мал, но такие индуцированные дипольные моменты могут вызвать вращательные переходы в неполярных молекулах. Если штарковское поле само изменяется, то возникают новые явления [290, 453], когда частота изменения становится сравнимой с шириной линии поглощения. Когда частота модуляции делается равной частоте спектральной линии, имеет место резонанс [ 181, эффект Штарка становится очень большим и за точкой резонанса меняет знак. [28]
Способность к поляризации самым непосредственным образом связана с физико-химической природой диэлектриков, что позволяет (по отношению к поляризационным процессам) подразделять их на два больших класса: неполярные ( нейтральные или бездипольные ) и полярные ( дипольные ).
Молекула любого вещества состоит из частиц (атомов или групп атомов, ионов), каждая из которых имеет определенный электрический заряд. В отсутствие внешнего электрического поля алгебраическая сумма всех зарядов равна нулю. Но их пространственное расположение в молекулах различных веществ может отличаться. Если заменить все положительные и отрицательные заряды одним положительным
Г лава 3. Поляризацияд иэлектрик ов
и одн им отрицательным, равными по модулю и расположенными в электрических центрах тяжести, то эти суммарные заряды могут либо совпадать в пространстве, л ибо не совпадать.
При совпадении центров тяжести положительных и отрицатель-
ных зарядов собственный электрический ( дипольный ) момент моле-
кулы μ 0 (Кл · м), которым она обладает в отсутствие электрического
(где q – суммарный положительный (или отрицательный) заряд молекулы; l – вектор, начало которого совпадает с центро м масс отрицательного заряда, а конец – с центром масс положительного заряда), равен нулю, так как l = 0.
Рис. 3.2. Молекулы одно атомного ( а ) и двухатомного газа ( б ). Распределение отрицательного заряда в молекулах показано различной интенсивностью серого цвета. Большей плотност и отрицательного заряда соответствует бóльшая интенсивность цвета. Символ ы «+» и «– » отража ют расположение центров тяжести пол ожительных и отри цательных зарядов в молекулах
Раздел 2. Диэлектрические материалы: основные положения физикидиэлектриков
Вышесказанное справедливо и для кристаллических твердых веществ. Если в отсутствие внешнего электрического поля в элементарной ячейке кристалла центры тяжести всех положительных и отрицательных зарядов совпадают, то ее собственный дипольный момент равен нулю ( μ 0 = 0), как и суммарный дипольный момент всего
Кристаллы подобного типа обладают центром симметрии и называ-
В диэлектриках даже в отсутствие внешнего электрического поля положительные и отрицательные заряды молекулы пространственно разнесены (имеется асимметрия в распределении электрических зарядов). Такая молекула представляет собой электрический диполь с отличным от нуля собственным постоянным электрическим моментом ( μ 0 ≠ 0) и является полярной ( дипольной ), как и вещество, образованное этими молекулами. Следует сказать, что электрический момент характеризует не только внутренние свойства диполя, но и его ориентацию в пространстве.
На рис. 3.3 схематично показана молекула ионного соединения (NaCl, KCl и т. п.), состоящая из положительных и отрицательных ионов, связанных между собой силами электростатического притяжения. Численное значение собственного дипольного момента μ 0 по-
лярной молекулы находится по выражению
где z – валентность иона; e – элементарный заряд,
электрона; l – плечо диполя.
Если несимметричная двухатомная молекула с частично ковалентной связью построена из атомов с различными электроотрицательностями, то она, как правило, полярна, поскольку валентные электроны (т. е. отрицательные заряды) смещены в сторону атома, имеющего бóльшую электроотрицательность. В качестве примера можно назвать молекулы CsCl, HF, HCl и др.
К полярным диэлектрикам относятся фенолформальдегидные
и эпоксидные смолы, кремнийорганические соединения, хлорированные углеводороды и др.
При оценке полярности вещества необходимо учитывать не условное написание химической формулы, а фактическое расположе-
Г лава 3. Поляризацияд иэлектрик ов
двуокись углерода СО 2 (рис.
3.4, а ), бензол С 6 Н 6 (рис. 3.4, в ), поли-
этилен (–С 2 Н 4 –) n (рис. 3.4, б ),
имеющий симметричное строение от-
дельных звеньев молекулярной
цепи относительно оси –С–С– и т. п.
Рис. 3.3. Схематическое изображение дипольной молекулы
Рис. 3.4. Схематическое изображение строения неполярных молекул :
а – двуокиси углерода; б – полиэтилена; в – бензола. Для двуо киси углерода показаны направления дипольных моментов полярны х фрагментов молекулы относительно ее оси симметри и (вертикальная ось)
Разд ел 2. Диэлектрически е материалы: основн ые положе ния физикидиэлектриков
Рис. 3.5. Схематическое изображение строения полярных молекул:
а – полихлорвинила; б – воды
В противоположность полиэтилену, полихлорвинил (–С 2 Н 3 Cl–) n (рис. 3.5, а ), имеющий несимметричное строение относитель но оси
–С–С–, полярен. Вода, химическая формула которой сходна с химической формулой двуокиси углерода, полярна, так как не имеет центра симметри и (рис. 3.5, б ).
В качестве примера в табл. 3.1 приведены численные значения
собственных д ипольн ых моме нтов μ 0 для некоторых ве ществ. Забегая вперед, о тметим, что полярные диэлектрики могут быть
турных единиц распределены по разным направлениям хаотически
и суммарный дипольн ый момент даже небольшого объема равен нулю. У сегнетоэлектриков дипольные моменты ориентированы параллельно
и суммарный дипольны й момент малых объемов не равен нулю.
Большая Энциклопедия Нефти и Газа
Индуцированный дипольный момент
Индуцированный дипольный момент относительно легко возникает в молекулах ароматических углеводородов. Поэтому ароматические соединения сравнительно хорошо экстрагируются избирательным растворителем. [1]
Индуцированный дипольный момент р пары соседних ионов противоположного знака равен ег. [2]
Индуцированный дипольный момент пропорционален напряженности поля. Коэффициент пропорциональности между Р и Е обычно обозначают ае и называют электронной поляризуемостью. [3]
Индуцированный дипольный момент / ш пропорционален напряженности поля Е, то есть / ш аЕ, где а характеризует степень поляризуемости индуцированной молекулы. [4]
Индуцированный дипольный момент в свою очередь создает электрическое поле, действующее на свободный заряд. [5]
Индуцированные дипольные моменты iei ( и tiei () в молекуле изменяются во времени с такой же частотой, как и падающая волна. Однако имеются следующие особенности такого излучения, Векторы § и В изменяются в одной фазе. Таким образом, для волны электрического поля падающего линейно поляризованного света при прохождении в оптически активном веществе должно наблюдаться вращение плоскости поляризации, так как кроме компоненты электрического поля в плоскости падающей волны появляется перпендикулярная компонента. [6]
Индуцированный дипольный момент имеет то же направление, что и постоянный диполь, вызвавший его появление. Взаимодействие постоянного диполя одной молекулы и наведенного им диполя второй понижает потенциальную энергию системы из двух молекул и упрочняет систему. Рассмотрим простейший и в то же время важный случай взаимодействия полярной и неполярной молекул. [7]
Индуцированные дипольные моменты согласно уравнению ( 2) уменьшаются экспоненциально с ростом числа слоев. [8]
Величина индуцированного дипольного момента зависит от силы электрического поля, и поэтому за меру такого дипольного момента принимается момент, возникающий при силе поля, равной единице. [11]
Величина индуцированного дипольного момента зависит от силы электрического поля и поэтому за меру такого дипольного момента принимается момент, возникающий при силе поля, равной единице. [12]
Согласно (9.12) индуцированный дипольный момент молекулы Р изменяется во времени; вследствие этого наблюдается рассеянный свет. [13]
Остальные компоненты индуцированного дипольного момента для дисперсии несущественны, однако они вместе с Z-компонентом определяют способность атома рассеивать падающее на него излучение. [14]
Среди ароматических углеводородов индуцированный дипольный момент возникает в тех из них, в которых ароматическое ядро не очень экранировано алифатическими цепями или нафтеновыми кольцами. Чем длиннее эти цепи или чем сложнее их конфигурация, тем больше осложняется возникновение в ароматических углеводородах наведенного дипольного момента и ассоциация с молекулами полярного растворителя. [15]
Теоретически электрический диполь определяется членом первого порядка мультипольного разложения ; он состоит из двух равных и противоположных зарядов, бесконечно близких друг к другу, хотя реальные диполи имеют разделенный заряд.
СОДЕРЖАНИЕ
Элементарное определение
и направлена от отрицательного заряда к положительному. Некоторые авторы могут разделить d пополам и использовать s = d / 2, поскольку эта величина представляет собой расстояние между любым зарядом и центром диполя, что приводит к коэффициенту два в определении.
Энергия и крутящий момент
На объект с электрическим дипольным моментом действует крутящий момент τ, когда он помещен во внешнее электрическое поле. Крутящий момент стремится выровнять диполь с полем. Диполь, расположенный параллельно электрическому полю, имеет меньшую потенциальную энергию, чем диполь, находящийся с ним под некоторым углом. Для пространственно однородного электрического поля E энергия U и крутящий момент определяются выражением τ <\ displaystyle <\ boldsymbol <\ tau>>>
Диполь, ориентированный параллельно или антипараллельно направлению увеличения неоднородного электрического поля (градиент поля), будет испытывать крутящий момент, а также силу в направлении своего дипольного момента. Можно показать, что эта сила всегда будет параллельна дипольному моменту независимо от со- или антипараллельной ориентации диполя.
Выражение (общий случай)
Это выражение эквивалентно предыдущему выражению в случае нейтральности заряда и N = 2. Для двух противоположных зарядов, обозначая расположение положительного заряда пары как r + и расположение отрицательного заряда как r — :
показывая, что вектор дипольного момента направлен от отрицательного заряда к положительному, поскольку вектор положения точки направлен наружу от начала координат к этой точке.
Дипольный момент особенно полезен в контексте общей нейтральной системы зарядов, например пары противоположных зарядов или нейтрального проводника в однородном электрическом поле. Для такой системы зарядов, представленной в виде массива пар противоположных зарядов, соотношение электрического дипольного момента выглядит следующим образом:
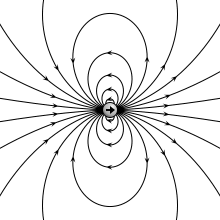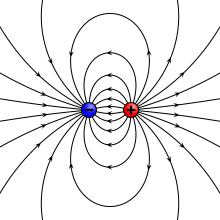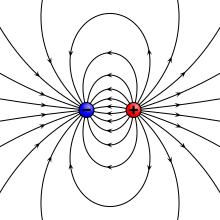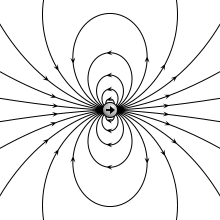
Потенциал и поле электрического диполя.
Идеальный диполь состоит из двух противоположных зарядов с бесконечно малым разделением. Мы вычисляем потенциал и поле такого идеального диполя, начиная с двух противоположных зарядов на расстоянии d> 0 и принимая предел при d → 0.
Два близко расположенных противоположных заряда ± q имеют потенциал вида:
где разделение зарядов:
Результат для дипольного потенциала также может быть выражен как:
который связывает дипольный потенциал с точечным зарядом. Ключевым моментом является то, что потенциал диполя падает быстрее с расстоянием R, чем потенциал точечного заряда.
Электрическое поле диполя представляет собой отрицательный градиент потенциала, приводящий к:
Таким образом, хотя два близко расположенных противоположных заряда не совсем идеальный электрический диполь (потому что их потенциал на коротких расстояниях не диполь), на расстояниях, намного больших, чем их разделение, их дипольный момент p появляется непосредственно в их потенциале и поле.
Плотность дипольного момента и плотность поляризации
Дипольный момент множества зарядов,
определяет степень полярности массива, но для нейтрального массива это просто свойство вектора массива без информации об абсолютном расположении массива. Дипольный момент плотность массива р ( г ) содержит как местоположение массива и его дипольный момент. Когда приходит время вычислить электрическое поле в некоторой области, содержащей массив, уравнения Максвелла решаются, и информация о массиве зарядов содержится в плотности поляризации P ( r ) уравнений Максвелла. В зависимости от того, насколько детально требуется оценка электрического поля, более или менее информация о массиве зарядов должна быть выражена через P ( r ). Как поясняется ниже, иногда достаточно точно взять P ( r ) = p ( r ). Иногда требуется более подробное описание (например, дополнение плотности дипольного момента дополнительной квадрупольной плотностью), а иногда даже более сложные версии P ( r ).
Формулировка уравнений Максвелла, основанная на разделении зарядов и токов на «свободные» и «связанные» заряды и токи, приводит к введению D- и P- полей:
с ρ b в качестве связанного заряда, под которым понимается разница между полной и свободной плотностями заряда.
Кстати, в отсутствие магнитных эффектов уравнения Максвелла указывают, что
Предположим, что заряды разделены на свободные и связанные, а потенциал разделен на
Далее обсуждается, как несколько различных описаний дипольного момента среды связаны с поляризацией, входящей в уравнения Максвелла.
Среда с зарядовой и дипольной плотностями
Как описано ниже, модель для плотности поляризационного момента p ( r ) приводит к поляризационному
ограничен той же моделью. Для плавно изменяющегося распределения дипольного момента p ( r ) соответствующая плотность связанного заряда просто
В качестве первого примера, связывающего дипольный момент с поляризацией, рассмотрим среду, состоящую из непрерывной плотности заряда ρ ( r ) и непрерывного распределения дипольного момента p ( r ). Потенциал в позиции r равен:
интеграл поляризации можно преобразовать:
где объемное интегрирование распространяется только до ограничивающей поверхности и не включает эту поверхность.
Потенциал определяется общим зарядом, который, как показано выше, состоит из:
Короче говоря, плотность дипольного момента p ( r ) играет роль плотности поляризации P для этой среды. Обратите внимание, что p ( r ) имеет ненулевую дивергенцию, равную плотности связанного заряда (как моделируется в этом приближении).
Можно отметить, что этот подход может быть расширен для включения всех мультиполей: диполя, квадруполя и т. Д. Используя соотношение:
плотность поляризации оказывается равной:
Поверхностный заряд
Выше было отложено обсуждение первого члена в выражении для потенциала, обусловленного диполями. Интегрирование расходимости приводит к поверхностному заряду. Рисунок справа дает интуитивное представление о том, почему возникает поверхностный заряд. На рисунке показан однородный массив идентичных диполей между двумя поверхностями. Внутри головы и хвосты диполей смежны и сокращаются. Однако на ограничивающих поверхностях отмены не происходит. Вместо этого на одной поверхности головки диполя создают положительный поверхностный заряд, а на противоположной поверхности хвосты диполя создают отрицательный поверхностный заряд. Эти два противоположных поверхностных заряда создают чистое электрическое поле в направлении, противоположном направлению диполей.
Этой идее придается математическая форма с использованием приведенного выше потенциального выражения. Если не брать в расчет бесплатную оплату, есть вероятность:
Используя теорему о дивергенции, член дивергенции превращается в поверхностный интеграл:
Если ограничивающая поверхность является сферой, а точка наблюдения находится в центре этой сферы, интегрирование по поверхности сферы равно нулю: положительный и отрицательный вклады поверхностного заряда в потенциал сокращаются. Однако, если точка наблюдения смещена от центра, может возникнуть чистый потенциал (в зависимости от ситуации), потому что положительные и отрицательные заряды находятся на разных расстояниях от точки наблюдения. Поле, обусловленное поверхностным зарядом, равно:
который в центре сферической ограничивающей поверхности не равен нулю ( поля отрицательных и положительных зарядов на противоположных сторонах центра складываются, потому что оба поля указывают одинаково), а вместо этого:
В частности, если ввести электрическую восприимчивость через приближение:
где E в этом случае и в дальнейшем представляет внешнее поле, индуцирующее поляризацию.
Всякий раз, когда χ ( r ) используется для моделирования скачка ступеньки на границе между двумя областями, ступенька создает слой поверхностного заряда. Например, интегрирование по нормали к ограничивающей поверхности от точки внутри одной поверхности до другой точки снаружи:
обязательно включает вклад поверхностного заряда.
Физически более реалистичное моделирование p ( r ) привело бы к быстрому падению плотности дипольного момента, но плавно до нуля на границе ограничивающей области, вместо того, чтобы делать внезапный шаг к нулевой плотности. Тогда поверхностный заряд не будет концентрироваться на бесконечно тонкой поверхности, а вместо этого, будучи дивергенцией плавно изменяющейся плотности дипольного момента, будет распределяться по тонкому, но конечному переходному слою.
Диэлектрическая сфера в однородном внешнем электрическом поле
Приведенные выше общие замечания о поверхностном заряде конкретизируются на примере диэлектрического шара в однородном электрическом поле. Обнаружено, что сфера принимает поверхностный заряд, связанный с дипольным моментом ее внутренней части.
а внутри сферы потенциал удовлетворяет уравнению Лапласа. Пропуская некоторые детали, решение внутри сферы таково:
находясь вне сферы:
Как следствие, потенциал:
который является потенциалом из-за приложенного поля и, кроме того, диполя в направлении приложенного поля (направление z ) дипольного момента:
или на единицу объема:
ведущее к полю внутри сферы:
Этот пример линейного диэлектрика показывает, что рассмотрение диэлектрической проницаемости эквивалентно модели однородного дипольного момента и приводит к нулевому заряду везде, кроме поверхностного заряда на границе сферы.
Общие СМИ
Если наблюдение ограничено областями, достаточно удаленными от системы зарядов, можно сделать мультипольное разложение точной плотности поляризации. При усечении этого разложения (например, с сохранением только дипольных членов или только дипольных и квадрупольных членов и т. Д. ) Результаты предыдущего раздела восстанавливаются. В частности, усекая расширение на дипольном члене, результат неотличим от плотности поляризации, создаваемой однородным дипольным моментом, ограниченным областью заряда. Для точности этого дипольного приближения, как показано в предыдущем разделе, плотность дипольного момента p ( r ) (которая включает не только p, но и местоположение p ) служит P ( r ).
Электрические дипольные моменты элементарных частиц
Дипольные моменты молекул
Дипольные моменты можно найти в обычных молекулах, таких как вода, а также в биомолекулах, таких как белки.
ϵ знак равно 1 + k ⟨ M Tot 2 ⟩ <\ displaystyle \ epsilon = 1 + k \ left \ langle <\ mathcal
Следовательно, в диэлектрическую проницаемость (и проводимость) входят оба члена. Этот подход можно обобщить для вычисления частотно-зависимой диэлектрической функции.