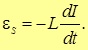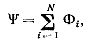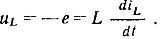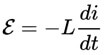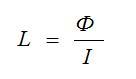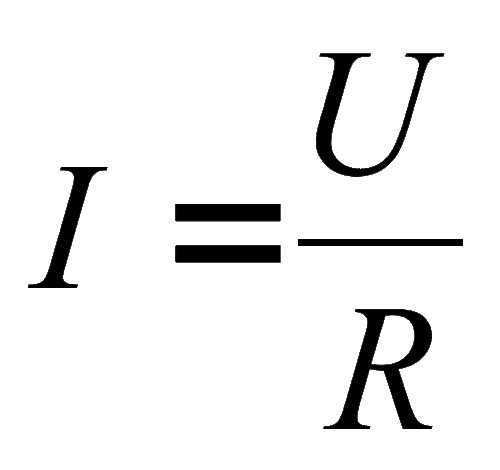что такое индуктивность в физике простыми словами
Индуктивность и явление самоиндукции
Люди, чья профессия или хобби связано с электрическим током, должны знать и разбираться в таких понятиях, как индуктивность и самоиндукция. Ведь подобные явления довольно часто используются в современном мире.
Что такое самоиндукция – для чайников
Любой электронный проводник имеет переменное магнитное поле, которое порождает дополнительный, так называемый индукционный ток. И если рассматривать в качестве проводника – электрическую цепь, то при изменении силы тока в ней изменится и магнитное поле, которое спровоцирует возникновение вихревого электрического поля.
Подобные явления станут причиной появления электродвижущей силы (ЭДС) в той же самой цепи, что и является самоиндукцией. Таким образом, самоиндукцией считается явление, во время которого в электрическом проводнике возникает ЭДС из-за изменения тока в самом проводнике. Именно самоиндукция мешает току приобрести определенное значение при резком замыкании или размыкании электрической цепи, так как ЭДС в проводнике во время нарастания тока направлена в противоположную сторону относительно источника питания и наоборот во время его уменьшения.
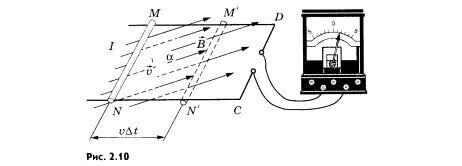
Явление самоиндукции можно наглядно увидеть при включении или выключении 2 одинаковых ламп, которые соединены параллельно.
При этом ЭДС самоиндукции можно рассчитать по формуле:
ЭДС измеряется в вольтах, когда единицей измерения магнитного поля является вебер.
Об индуктивности простыми словами
Индуктивностью является физическая величина, которая была введена с целью оценки способности электрического проводника противодействовать току. Т.е. индуктивность, или как ее еще называют – коэффициент самоиндукции, показывает зависимость Ɛ от свойств проводника и от магнитной проницаемости среды, в которой он находится. Единицей измерения величины является генри (Гн).
Если рассмотреть величину на примере катушки индуктивности, то можно понять, что ее показатели будут изменяться в зависимости от числа витков катушки, а также ее размеров и формы. Чем больше количество витков, тем больше индуктивность. Данная величина также будет увеличена, если внутрь катушки будет помещен сердечник, так как изменится относительная магнитная проницаемость среды, в которой находится проводник. Данную зависимость можно увидеть на схеме.
Если посмотреть на формулу зависимости ЭДС от индуктивности, то можно понять, что чем больше будет величина, тем заметнее будет электродвижущая сила, что говорит о их прямой пропорциональности. Следуя из этого, можно сделать вывод, что индуктивность выступает неким «хранилищем» энергии, которое открывается в момент изменения тока.
При этом L равно магнитному полю (Ф) деленному на силу тока (I).
Польза и вред
Такое явление, как самоиндукция, большинство людей наблюдают ежедневно, даже не осознавая этого. Так, например, принцип работы люминесцентных трубчатых ламп основан именно на явлении самоиндукции. Также данное явление можно наблюдать в цепи зажигания транспортных средств, работающих на бензине. Это возможно благодаря наличию катушки индуктивности и прерывателя. Так, в момент, когда через катушку проходит ток, прерыватель разрывает цепь питания катушки, в результате чего и образуется ЭДС, которая далее приводит к тому, что импульс более 10 кВ поступает на свечи зажигания.
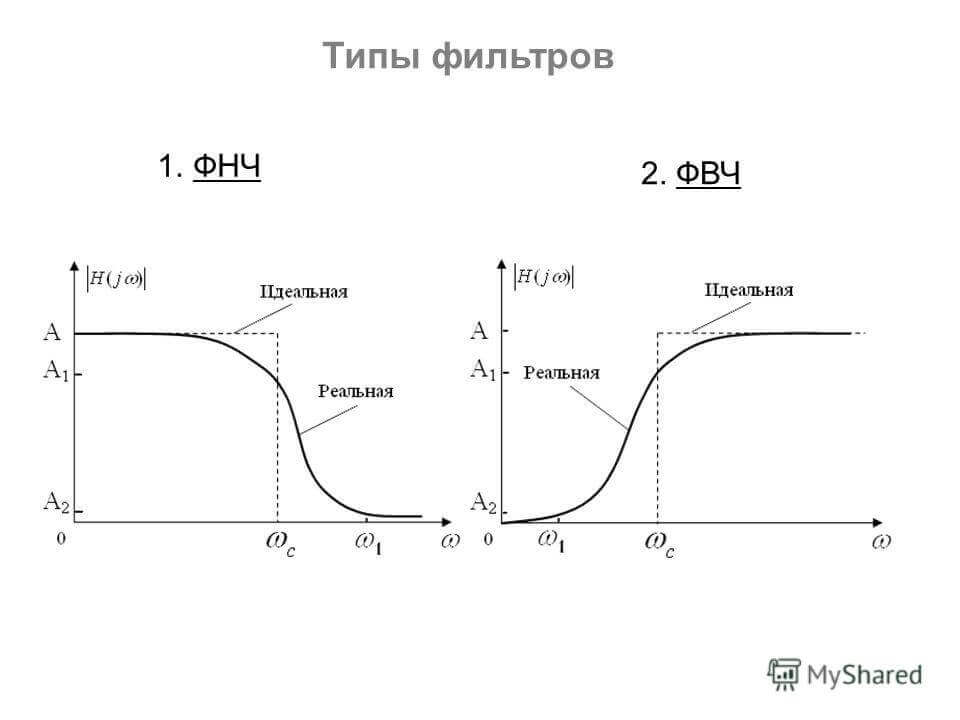
Явление самоиндукции также приносит пользу, убирая лишнюю пульсацию, частоты или различные шумы в музыкальных колонках или другой аудиотехнике. Именно на ней основано работа различных «шумовых» фильтров.
Однако самоиндукция способна приносить не только пользу, но и заметный вред. Особенно часто она вредит различным выключателям, рубильникам, розеткам и другим устройствам, размыкающим электрическую цепь. Ее негативное воздействие на электроприборы можно заметить невооруженным глазом: искра в розетке в момент вытаскивания вилки, работающего фена и есть проявление сопротивления изменению силы тока.
Именно поэтому лампочки чаще всего перегорают именно в момент выключения света, а не наоборот. Это связано с тем, что сопротивление приводит к выгоранию контактов и накоплению цепей с токами в различных электроприборах, что в свою очередь представляет собой довольно серьезную техническую проблему.
Индуктивность и самоиндукция – незнакомые многим термины, с которыми люди встречаются ежедневно. И если первый термин является физической величиной, обозначающей способность проводника препятствовать изменению напряжения, то второй объясняет появление ЭДС индукции в том же проводнике.
Индуктивность
Выше мы рассматривали два основных понятия в электротехнике — идеальный генератор напряжения и идеальный генератор тока.
Идеальный генератор напряжения выдает заданное напряжения U (давление в водопроводной аналогии) на любой нагрузке (сопротивлении внешней цепи).
При этом в соответствии с законом Ома I=U/R, даже если R стремится к нулю, а ток возрастает до бесконечности.
Внутренне сопротивление идеального генератора напряжения равно 0.
Идеальный генератор тока выдает заданный ток I (поток в водопроводной аналогии), даже если сопротивление внешней цепи стремится к бесконечности. Напряжение на нагрузке при этом также стремится к бесконечности U=I*R.
Внутреннее сопротивление идеального генератора тока равно ∞.
Тут можно увидеть определенную симметрию, дуализм.
Мы рассматривали конденсатор С который может накапливать заряд (потому и называется — емкость) С=Q/U. Чем больше емкость, тем медленнее растет напряжение (давление) при закачке в конденсатор заряда U=Q/C.
Если емкость заряда очень большая (стремится к бесконечности), то такой конденсатор бесконечной емкости будет являться идеальным генератором напряжения. Он никогда не разрядится и при этом может выдать ток любой величины, и напряжение на нем будет оставаться постоянным.
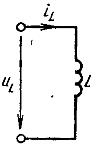
Симметричным (дуальным) к конденсатору элементом будет являться индуктивность. Индуктивность обозначается буквой L (см схему ниже).
Обычно сам электронный компонент называется катушка индуктивности, а его параметр — индуктивность L.

Если конденсатор является генератором напряжения, то индуктивность является генератором тока. Индуктивность стремиться поддерживать ток в цепи постоянным, то есть препятствует изменению тока в цепи.
Индуктивность бесконечной величины является идеальным генератором тока, то есть будет бесконечно гнать заданный ток I независимо от сопротивления нагрузки.
Это похоже как если вы подойдете к стоящей на рельсах вагонетке и станете ее толкать (приложите к ней силу). Вагонетка начнет медленно разгоняться и «ток все быстрее и быстрее побежит по проводам». А потом попробуйте вагонетку тормозить и она будет медленно останавливаться.
Так и в индуктивности, после подачи напряжения ток будет постепенно расти (вагонетка разгоняется), а при подаче напряжения другой полярности — постепенно уменьшаться (вагонетка тормозится).
Отсюда следует вывод «Поезд мгновенно остановить нельзя!»
«Ток в индуктивности мгновенно остановить нельзя!»
То есть даже если щелкнуть выключателем S4 на схеме и разомкнуть цепь, ток в первый момент после этого будет продолжать идти! На практике это приводит к тому, что в момент размыкания контактов в выключателе между ними будет проскакивать искра.
Сопротивление при размыкании контактов увеличивается до бесконечности (в реальности до очень больших величин) и протекающий ток создаст на этом сопротивлении напряжение очень большой величины, так что воздушный промежуток между контактами будет пробит.
“При изменении тока в контуре пропорционально меняется и магнитный поток через поверхность, ограниченную этим контуром. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС. Это явление называется самоиндукцией. Направление ЭДС самоиндукции всегда оказывается таким, что при возрастании тока в цепи ЭДС самоиндукции препятствует этому возрастанию (направлена против тока), а при убывании тока — убыванию (сонаправлена с током). Явление самоиндукции проявляется в замедлении процессов исчезновения и установления тока.”
Тут есть некий момент — постоянный ток это ток, который не меняется со временем, то, что называется «постоянная составляющая» частотой равной 0 Гц. Ее конденсатор не пропускает. Совсем.
А вот индуктивность совсем не пропускает переменный ток бесконечной частоты. А просто переменный ток любой конечной частоты немножко пропускает.
Но к понятию напряжения переменного тока мы вернемся позже.

При подаче на индуктивность постоянного напряжения ток в ней линейно возрастает со временем.
Мы помним аналогичную картину для конденсатора.
Напряжение на конденсаторе линейно возрастает при его заряде постоянным током.
А что будет, если запитать индуктивность от генератора тока?

Ну тут из серии «кто кого заборет — слон или кит».
Цепи, содержащие конденсатор и индуктивность
Как было отмечено выше, индуктивность в электротехнике играет ту же роль, что масса в механике. А что является аналогом конденсатора в механике? Конденсатор является генератором напряжения, то есть создает силу, которая двигает поток заряда по проводам. Выше мы приводили аналог конденсатора в виде водонапорной башни, которая заполняется водой (зарядом) и давление (напряжение) в ней увеличивается.
Но можно также представить конденсатор в виде пружины — при заряде пружина сжимается и сила сжатия (напряжение) увеличивается. Емкость в этом случае величина обратная жесткости пружины. Чем пружина жестче, тем быстрее возрастает сила при сжатии. То есть соединение конденсатора и индуктивности эквивалентно вагонетке закрепленной на пружине. )
Что же будет происходить, если конденсатор соединить с индуктивностью, например как в схеме на рис. 16

Пусть конденсатор С заряжен до напряжения U. Ключ S2 замыкается и в цепи начинает течь ток. Это эквивалентно тому, как если бы мы сжали пружину и затем в какой-то момент отпустили (замкнули ключ S2).
То есть цепь пришла в состояние когда конденсатор заряжен, ток в ней равен нулю.
Хм.. но это то же состояние, с которого мы начали, только полярность напряжения противоположная. Следовательно процесс повторится, только ток потечет уже в другую сторону и система вернется в исходное состояние. Вагонетка поедет обратно, проедет положение равновесия и по инерции снова сожмет пружину.
Возникнет колебательный процесс. То есть вагонетка на пружине так и будет кататься туда-сюда и в отсутствие потерь энергии (трения) этот процесс будет длиться бесконечно.
Таким образом соединение конденсатора с индуктивностью образует колебательное звено. Такие звенья широко используются в электротехнике для создания генераторов и фильтров напряжения переменного тока.
Понятие переменного тока рассмотрим в следующей статье.
UPD.
Поскольку возник диспут экспоненциально ли растет ток при подключении катушки индуктивности к генератору напряжения или линейно, скажу еще пару слов по этому вопросу.
Откуда же берется экспонента роста тока в схеме на рис.13?
Ответ- ниоткуда. Ее там нет. Ток растет линейно и зависимость тока от напряжения описывается формулой
ЭДС самоиндукции в цепи прямо пропорциональна скорости изменения силы тока в этой цепи.
Чтобы обеспечить U=const (а U – это производная от тока в катушке), ток должен линейно расти.
А откуда тогда вообще зашел разговор об экспоненте? А зашел он потому, что ток линейно растет только в идеальном случае — в схеме с идеальным генератором напряжения (бесконечной мощности и с нулевым внутренним сопротивлением) и идеальной индуктивностью (с нулевым внутренним сопротивлением).
В реальном случае с учетом внутреннего сопротивления схема будет выглядеть так.

На схеме рис.17 R символизирует собой внутреннее сопротивление генератора и катушки индуктивности. (они все равно включены последовательно, поэтому можно обойтись одним R, как суммой этих сопротивлений)
Вот в этом случае и получится такой экспоненциальный график роста тока в индуктивности.


зы. В интернете столько разнообразной ереси на тему катушек индуктивности. Просто диву даешься.
«Катушка индуктивности обладает также очень интересным свойством. При подаче на катушку постоянного напряжения, в катушке возникает на короткий промежуток времени противоположное напряжение. Это противоположное напряжение называется ЭДС самоиндукции. Эта ЭДС зависит от значения индуктивности катушки. Поэтому, в момент подачи напряжения на катушку сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение, в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения.»
Ну.. поскольку про резистор в цепи ничего не сказано, то не на короткий промежуток, а пока входное напряжение не будет снято. Вторая часть звучит бредово, но направление верное — ток с цепи растет от нуля до.. без резистора до бесконечности, с резистором до I=Uвх/R.
Предположим, что обычная катушка индуктивности подключена к источнику напряжения через ключ. При замыкании ключа на индуктивность подается напряжение, вызывающее быстрое изменение протекающего через нее тока. Когда приложенное напряжение увеличивается от нуля до пикового значения (за короткое время), индуктивность противодействует изменяющемуся через нее току, индуцируя напряжение, противоположное по полярности приложенному напряжению. Индуцированное напряжение при подаче питания на катушку индуктивности называется обратной ЭДС и определяется по формуле 1:
VL = – L*(di/dt), (1)
где:
VL – напряжение (обратная ЭДС), индуцированная на катушке;
L – индуктивность катушки;
di/dt – скорость изменения тока во времени.
Видимо здесь попытались описать начальный момент возникновения ЭДС самоиндукции, но получилась ерунда. Говорить, что «индуцированное напряжение противоположно по полярности приложенному напряжению» это то же самое, что «падение напряжения на резисторе противоположно по полярности приложенному напряжению.» Ага, точно, приложенное напряжение сложили с падением напряжения и после резистора получили 0. Так и есть, лол.
«ЭДС самоиндукции» в катушке это аналог «падения напряжения» на резисторе. Только в резисторе электрическая энергия рассеивается, переходит в тепло, а в индуктивности — накапливается, переходит в энергию магнитного поля. В водопроводной аналогии индуктивность это такая турбинка, вставленная в водопроводную трубу, и которая имеет момент инерции. Турбинка пропускает воду только когда вращается. И вот крантель открыли, давление к турбинке приложили, она начала вращаться и пошел ток дальше по трубе. И чем быстрее турбинка вращается, тем больше ее пропускная способность. Турбинка раскручивается, ток возрастает и так до бесконечности. Это если нет потерь энергии — резистора. А если есть резистор (трение), то часть давления расходуется на преодоление трения. И когда вся входная энергия будет расходоваться на трение, турбинка перестанет ускоряться и ток достигнет максимальной величины.

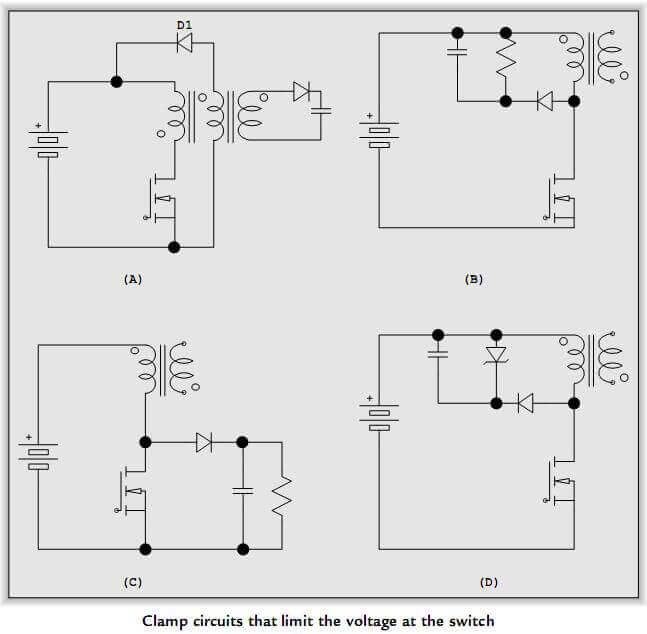
Картинка неправильная. В правильном варианте при отключении источника, подключался резистор и цепь оставалась замкнутой.
Рассмотрим следующую цепь

Вопрос на засыпку: Чему будет равно напряжение на индуктивности в первый момент после переключения ключа S из верхнего положения в нижнее?
Hint: Не надо выносить себе мозг, пытаясь сообразить с каким там знаком возникнет ЭДС самоиндукции и что с ней будет дальше. Надо применять простое правило:
Ток в индуктивности в первый момент времени после переключения сохраняется неизменным.
Дальше применять закон Ома.
Что такое индуктивность

В отличие от индуктивности в индуктивной катушке имеют место также запасание энергии электрического поля и преобразование электрической энергии в другие виды энергии, в частности в тепловую.
Количественно способность реального и идеализированного элементов электрической цепи запасать энергию магнитного поля характеризуется параметром, называемым индуктивностью.
Таким образом термин «индуктивность» применяется как название идеализированного элемента электрической цепи, как название параметра, количественно характеризующего свойства этого элемента, и как название основного параметра индуктивной катушки.
Рис. 1. Условное графическое обозначение индуктивности
Связь между напряжением и током в индуктивной катушке определяется законом электромагнитной индукции, из которого следует, что при изменении магнитного потока, пронизывающего индуктивную катушку, в ней наводится электродвижущая сила е, пропорциональная скорости изменения потокосцепления катушки ψ и направленная таким образом, чтобы вызываемый ею ток стремился воспрепятствовать изменению магнитного потока:
Потокосцепление катушки равно алгебраической сумме магнитных потоков пронизывающих ее отдельные витки:
где N — число витков катушки.

Первая составляющая представляет собой магнитный поток, вызванный протекающим по катушке током, вторая — определяется магнитными полями, существование которых не связано с током катушки — магнитным полем Земли, магнитными полями других катушек и постоянных магнитов. Если вторая составляющая магнитного потока вызвана магнитным полем другой катушки, то ее называют магнитным потоком взаимоиндукции.

здесь еси — ЭДС самоиндукции, евп — ЭДС внешних полей.
Если магнитные потоки внешних по отношению к индуктивной катушке полей равны нулю и катушку пронизывает только поток самоиндукции, то в катушке наводится только ЭДС самоиндукции.
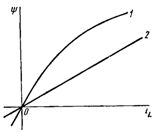
В частном случае, например для катушки без магнитного сердечника, эта зависимость может быть линейной (рис. 2, кривая 2).
В системе единиц СИ индуктивность выражают в генри (Гн).
При анализе цепей обычно рассматривают не значение ЭДС, наведенной в катушке, а напряжением на ее зажимах, положительное направление которого выбирают совпадающим с положительным направлением тока:
Для линейной индуктивности напряжение на ее зажимах пропорционально скорости изменения тока. При протекании через индуктивность постоянного тока напряжение на ее зажимах равно нулю, следовательно, сопротивление индуктивности постоянному току равно нулю.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Индуктивность что это простыми словами
в электродинамике (коэффициент самоиндукции) (от лат. inductio – наведение, побуждение) – параметр электрич. цепи, определяющий величину эдс самоиндукции, наводимой в цепи при изменении протекающего по ней тока и (или) при её деформации. Термин «И.» употребляется также для обозначения элемента цени (двухполюсника), определяющего её индуктивные свойства (синоним – катушка самоиндукции).И. является количеств. характеристикой эффекта самоиндукции, открытого независимо Дж. Генри (J. Henry) в 1832 и М. Фарадеем (М. Faraday) в 1835. При изменении тока в цепи и (или) при её деформации происходит изменение магн. поля, к-рое, в соответствии с законом индукции, приводит к возникновениювихревого электрич. поля E(r, t )с отличной от нуля циркуляцией
по замкнутым контурам li;пронизываемым магн. потоком Ф i. Внутри проводника вихревое поле Е взаимодействует с порождающим его током и оказывает противодействие изменению магн. потока (Ленца правило). Циркуляция Ei и магн. поток Ф i существенно зависят от выбора контура li внутри проводника конечной толщины. Однако при медленных движениях и квазистацнонарных процессах, когда полный ток
(j – плотностьтока) одинаков для всех нормальных сечений провода S пр, допустим переход к усреднённым характеристикам: эдс самоиндукции E си= )и сцепленному с проводящим контуром магн. потоку Ф=i>. В предположении о том, что линии тока замыкаются сами на себя при одном обходе по контуру,
Ф=L.I (в СИ), Ф= 1 /c(LI)(в системе СГС). (1)
Коэф. L и Lназ. И. Величина L измеряется в генри, L – в см.
Производная по времени от И. определяет ту часть E си, к-рая связана с деформацией проводящего контура; в случае недеформируемых цепей и квазистационарных процессов И. может быть вынесена из-под знака дифференцирования. энергия, запасённая в создаваемом им магн. поле, записывается в форме, аналогичной выражению для кинетич. энергии.
W m = 1 /2LI 2 (в СИ), W m = 1 /2c 2 LI 2 (в системе СГС). (3)
Соотношение (3) позволяет различать И. внутреннюю Li, определяющую энергию магн. поля, сосредоточенного в проводниках, и внешнюю Le, связанную с внеш. магн. полем (L=Li+Le, L=Li+Le). В важном частном случае токовой цепи, выполненной из проводов, толщина к-рых мала по сравнению с радиусамиих изгибов или расстояниями между соседними проводами, можно считать, что структура токов и ближнего магн. поля такая же, как и для прямого провода того же сечения (подобные проводники наз. квазилинейными). В приближении заданной структуры токов, не зависящей от способа их возбуждения, И. определяется только геометрией проводящей цепи (толщиной и длиной проводов и их формой). Для квазилинейного провода кругового сечения Li=(m /8p)mil (l – длина провода, mi – магн. проницаемость проводника), а внешняя И. может быть представлена как индуктивность взаимная двух параллельных бесконечно тонких проводящих нитей, одна из к-рых (l1) совпадает с осевой линией проводника, а другая (l2) совмещена с его поверхностью:
где r1, r2 – радиус-векторы точек на контурах ll, l2,m е – магн. проницаемость окружающей среды [для аналогия, соотношений в системе СГС L «(m /4p)L]. Из (4) видно, что Le логарифмически расходится при стремлении радиуса провода к нулю, поэтому идеализацией бесконечно тонкого провода нельзя пользоваться при описании явлений самоиндукции. Приближённые вычисления интеграла в (4) с учётом внутренней И. дают:
где l и а – длина и радиус провода. Это выражение обладает логарифмич. точностью – его относит. погрешность порядка величины l/ln(l/a). Примеры типичных электрич. цепей и выражения для их И. приведены на рис. 1 и 2.
Рис. 1. Круговой виток. Индуктивность витка (проводящего тора): L=m R(ln(8R/r)-2+ 1 /4mi), Гн, r
Особое значение в электротехнике и радиотехнике имеют проволочные катушки с достаточно плотной намоткой – соленоиды (рис. 3), применяемые для увеличения И. Поскольку И. цепей, в к-рые включены соленоиды, ими в основном и определяются, принято говорить об И. соленоида. Под величиной И. идеальногосоленоида понимают И. эфф. проводящей поверхности (совпадающей с его каркасом), по к-рой протекают азимутальные поверхностные токи с плотностью j пов=Ik (I – ток в соленоиде, k – число витков на единице длины).
Понятие И. допускает обобщение на быстропеременные гармонич. ехр(iwt)-процессы, при описании к-рых нельзя пренебрегать запаздыванием эл.-магп. взаимодействий, скин-эффектом в проводниках, дисперсией среды. Комплексные амплитуды тока Iw и эдс самоиндукции Ew связаны соотношением:
И. L(w) зависит от частоты (как правило, уменьшается с её ростом). Эфф. сопротивление RL(w) определяет часть энергетич. потерь, в т. ч. потери на излучение, и связано с L(w) Крамерса – Кронига соотношением:
где интеграл берётся в смысле гл. значения. На низких частотах сопротивлением RL(w) можно пренебречь, тогда Ew и Iw сдвинуты по фазе на p/2. Соотношение (3) для высокочастотных процессов преобразуется к виду:
Величина L Д(I)=d Ф /dIназ. дифференциальной (или иногда динамической) И. Выражение для запасённой энергии пост. тока приобретает вид:
B линейном приближении (при I «0) L Д «L и выражения (10), (11) переходят в (2) и (3) соответственно. Лит.: Тамм И. Е., Основы теории электричества9 изд., М., 1976; Калантаров П. Л., Цейтлин Л. А. Расчет индуктивностей, 3 изд., Л., 1986; Ландау Л. Д. Лифшиц Е. М., Электродинамика сплошных сред, 2 изд. М., 1982. М. А. Миллер, Г. В. Пермитин
Определение
Самоиндукцией называется появление в проводнике электродвижущей силы (ЭДС), направленной в противоположную сторону относительно напряжения источника питания при протекании тока. При этом оно возникает в момент, когда сила тока в цепи изменяется. Изменяющийся электрической ток порождает изменяющееся магнитное поле, оно в свою очередь наводит ЭДС в проводнике.
Это похоже на формулировку закона электромагнитной индукции Фарадея, где сказано:
При прохождении магнитного потока через проводник, в последнем возникает ЭДС. Она пропорциональна скорости изменения магнитного потока (мат. производная по времени).
E=dФ/dt,
Где E – ЭДС самоиндукции, измеряется в вольтах, Ф – магнитный поток, единица измерения – Вб (вебер, он же равен В/с)
Индуктивность
Мы уже сказали о том, что самоиндукция присуща индуктивным цепям, поэтому рассмотрим явление самоиндукции на примере катушки индуктивности.
Катушка индуктивности – это элемент, который представляет собой катушку из изолированного проводника. Для увеличения индуктивности увеличивают число витков или внутрь катушки помещают сердечник из магнитомягкого или другого материала.
Единица измерения индуктивности – Генри (Гн). Индуктивность характеризует то, насколько сильно проводник противодействует электрическому току. Так как вокруг каждого проводника, по которому протекает ток, образуется магнитное поле, и, если поместить проводник в переменное поле – в нем возникнет ток. В свою очередь магнитные поля каждого витка катушки складываются. Тогда вокруг катушки, по которой протекает ток, возникнет сильное магнитное поле. При изменении его силы в катушке будет изменяться и магнитный поток вокруг неё.
Согласно закону электромагнитной индукции Фарадея, если катушку будет пронизывать переменный магнитный поток, то в ней возникнет ток и ЭДС самоиндукции. Они будут препятствовать току, который протекал в индуктивности от источника питания к нагрузке. Их еще называют экстратоки ЭДС самоиндукции.
Формула ЭДС самоиндукции на индуктивности имеет вид:
То есть чем больше индуктивность, и чем больше и быстрее изменился ток – тем сильнее будет всплеск ЭДС.
При возрастании тока в катушке возникает ЭДС самоиндукции, которая направлена против напряжения источника питания, соответственно возрастание тока замедлится. То же самое происходит при убывании – самоиндукция приведет к появлению ЭДС, которое будет поддерживать ток в катушке в том же направлении, что и до этого. Отсюда следует, что напряжение на выводах катушки будет противоположным полярности источника питания.
На рисунке ниже вы видите, что при включении/отключении индуктивной цепи ток не резко возникает, а изменяется постепенно. Об этом говорят и законы коммутации.
Другое определение индуктивности звучит так: магнитный поток пропорционален току, но в его формуле индуктивность выступает в качестве коэффициента пропорциональности.
Трансформатор и взаимоиндукция
Если расположить две катушки в непосредственной близости, например, на одном сердечнике, то будет наблюдаться явление взаимоиндукции. Пропустим переменный ток по первой, тогда её переменный поток будет пронизывать витки второй и на её выводах появится ЭДС.
Это ЭДС будет зависеть от длины провода, соответственно количества витков, а также от величины магнитной проницаемости среды. Если их расположить просто около друг друга — ЭДС будет низким, а если взять сердечник из магнитомягкой стали – ЭДС будет значительно больше. Собственно, так и устроен трансформатор.
Интересно: такое взаимное влияние катушек друг на друга называют индуктивной связью.
Польза и вред
Если вам понятна теоретическая часть, стоит рассмотреть где применяется явление самоиндукции на практике. Рассмотрим на примерах того, что мы видим в быту и технике. Одно из полезнейших применений – это трансформатор, принцип его работы мы уже рассмотрели. Сейчас встречаются все реже, но ранее ежедневно использовались люминесцентные трубчатые лампы в светильниках. Принцип их работы основан на явлении самоиндукции. Её схемы вы можете увидеть ниже.
После подачи напряжения ток протекает по цепи: фаза — дроссель — спираль — стартер — спираль — ноль.
Или наоборот (фаза и ноль). После срабатывания стартера, его контакты размыкаются, тогда дроссель (катушка с большой индуктивностью) стремится поддержать ток в том же направлении, наводит ЭДС самоиндукции большой величины и происходит розжиг ламп.
Аналогично это явление применяется в цепи зажигания автомобиля или мотоцикла, которые работают на бензине. В них в разрыв между катушкой индуктивности и минусом (массой) устанавливают механический (прерыватель) или полупроводниковый ключ (транзистор в ЭБУ). Этот ключ в момент, когда в цилиндре должна образоваться искра для зажигания топлива, разрывает цепь питания катушки. Тогда энергия, запасенная в сердечнике катушки, вызывает рост ЭДС самоиндукции и напряжение на электроде свечи возрастает до тех пор, пока не наступит пробой искрового промежутка, или пока не сгорит катушка.
В блоках питания и аудиотехнике часто возникает необходимость убрать из сигнала лишние пульсации, шумы или частоты. Для этого используются фильтры разных конфигурации. Один из вариантов это LC, LR-фильтры. Благодаря препятствию роста тока и сопротивлению переменного тока, соответственно, возможно добиться поставленных целей.
Вред ЭДС самоиндукции приносит контактам выключателей, рубильников, розеток, автоматов и прочего. Вы могли заметить что, когда вытаскиваете вилку работающего пылесоса из розетки, очень часто заметна вспышка внутри неё. Это и есть сопротивление изменению тока в катушке (обмотке двигателя в данном случае).
В полупроводниковых ключах дело обстоит более критично – даже небольшая индуктивность в цепи может привести к их пробою, при достижении пиковых значений Uкэ или Uси. Для их защиты устанавливают снабберные цепи, на которых и рассеивается энергия индуктивных всплесков.
Заключение
Подведем итоги. Условиями возникновения ЭДС самоиндукции является: наличие индуктивности в цепи и изменение тока в нагрузке. Это может происходить как в работе, при смене режимов или возмущающих воздействиях, так и при коммутации приборов. Это явление может нанести вред контактам реле и пускателей, так как приводит к образованию дуги при размыкании индуктивных цепей, например, электродвигателей. Чтобы снизить негативное влияние большая часть коммутационной аппаратуры оснащается дугогасительными камерами.
В полезных целях явление ЭДС используется довольно часто, от фильтра для сглаживания пульсаций тока и фильтра частот в аудиоаппаратуре, до трансформаторов и высоковольтных катушек зажигания в автомобилях.
Напоследок рекомендуем просмотреть полезное видео по теме, на которых кратко и подробно рассматривается явление самоиндукции:
Надеемся, теперь вам стало понятно, что такое самоиндукция, как она проявляется и где ее можно использовать. Если возникли вопросы, задавайте их в комментариях под статьей!
Материалы по теме:
Любая катушка индуктивности, как ни странно, обладает индуктивностью 🙂 Индуктивность катушки измеряется в Генри (Гн), обозначается буковкой L и замеряется LC – метром. Что такое индуктивность? Давайте разбираться. Если через проводок прогнать электрический ток, то он вокруг себя создаст магнитное поле:
А давайте возьмем и намотаем в спиральку этот провод и подадим на его концы электрический ток:
И у нас получилась вот такая картина с магнитными силовыми линиями:
Грубо говоря, чем больше линий магнитного поля пересекут площадь этого соленоида, получается площадь цилиндра, тем больше будет магнитный поток (Ф). Так как по всей этой конструкции течет электрический ток, то значит в этот момент он обладает какой-то Силой тока (I). А коэффициент между магнитным потоком и силой тока называется индуктивностью, и вычисляется так:
С научной же точки зрения, индуктивность – это способность извлекать энергию из источника электрического тока и сохранять ее в виде магнитного поля. Если ток в катушке увеличивается, магнитное поле вокруг катушки расширяется, а если ток уменьшается – магнитное поле сжимается. Катушка индуктивности обладает также очень интересными свойствами. При подаче на катушку электрического тока постоянного напряжения, в катушке возникает напряжение, противоположное напряжению электрического тока и оно потом исчезает через несколько долей секунд. Это противоположное напряжение называется ЭлектроДвижущейСилой самоиндукции, или просто – ЭДС самоиндукции. Это ЭДС зависит от индуктивности катушки. Поэтому в момент подачи напруги на катушку Сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение,в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения, согласно Закон Ома:
где I – сила тока в катушке, U – напряжение в катушке, R – сопротивление катушки.
Как мы видим по формуле, напряжение меняется от нуля и до напряжения, подаваемого в катушку, следовательно и ток тоже будет меняться от нуля и до какого то значения. Сопротивление катушки постоянное.
И второй прикол в катушке индуктивности заключается в том, что если мы разомкнем цепь катушка индуктивности – источник тока, то у нас ЭДС самоиндукции будет приплюсовываться к напряжению, которое мы подали на катушку. Следовательно и ток будет в самом начале больше, а потом тихонько спадет до нуля. Время спада силы тока также зависит от индуктивности катушки.
Сделаем первые выводы о работе катушки индуктивности при подаче на нее постоянного тока. При подаче на катушку электрического тока, сила тока будет плавно увеличиваться, а при снятии электрического тока с катушки, сила тока резко возрастет в катушке и плавно убавиться до нуля. Короче говоря,сила тока в катушке мгновенно измениться не может. Это в электронике называют первым законом коммутации. Уфф, ну все, самое тяжелое позади :-).
Катушки индуктивности делятся в основном на два класса: с магнитным и немагнитным сердечником. Снизу на фото катушка с немагнитным сердечником.
Но где у нее сердечник? Воздух – это немагнитный сердечник :-). Такие катушки также могут быть намотаны на какой-нибудь цилиндрической бумажной трубочке. Индуктивность катушек с немагнитным сердечником используется, когда индуктивность не превышает 5 миллиГенри.
А вот катушки индуктивности с сердечником:
В основном используют сердечники из феррита и железных пластин. Сердечники повышают индуктивность катушек в разы. Сердечники в виде кольца (тороидальные) позволяют получить большую индуктивность, нежели просто сердечники из цилиндра.
Для катушек средней индуктивности используются ферритовые сердечники:
Катушки с большой индуктивностью делают как трансформатор с железным сердечником, но есть одно различие: у них имеется только одна первичная обмотка:
От каких факторов зависит индуктивность катушки? Давайте проведем несколько опытов. Я намотал катушку с немагнитным сердечником. Ее индуктивность настолько мала, что LC – метр мне показывает ноль.
Имеется ферритовый сердечник
Начинаю вводить катушку в сердечник на самый край
LC-метр показывает 21 микроГенри.
Ввожу катушку на середину феррита
35 микроГенри. Уже лучше.
Продолжаю вводить катушку на правый край феррита
20 микроГенри. Делаем вывод, самая большая индуктивность на цилиндрическом феррите возникает в его середине. Поэтому, если будете мотать на цилиндрике, старайтесь мотать в середине феррита. Это свойство используется для плавного изменения индуктивности в переменных катушках индуктивности:
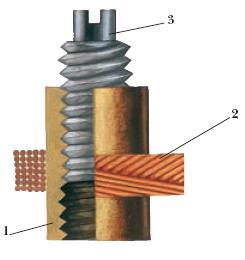
1 – это каркас катушки
2 – это витки катушки
3 – сердечник, у которого сверху пазик по маленькую отвертку. Вкручивая или выкручивая сердечник, мы тем самым изменяем индуктивность катушки.
Экспериментируем дальше. Давайте попробуем сжимать и разжимать витки катушки. Для начала ставим ее в середину и начинаем сжимать витки
Индуктивность стала почти 50 микроГенри!
А давайте-ка попробуем расправим витки по всему ферриту
13 микроГенри. Делаем вывод: для максимальной индуктивности мотать катушку надо «виток к витку».
Убавим витки катушки в два раза. Было 24 витка, стало 12.
Совсем маленькая индуктивность. Убавил количество витков в 2 раза, индуктивность уменьшилась в 10 раз. Вывод: чем меньше количество витков – тем меньше индуктивность. Индуктивность меняется не прямолинейно виткам.
Давайте поэкспериментируем с ферритовым кольцом.