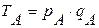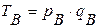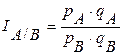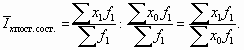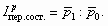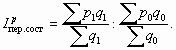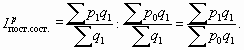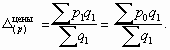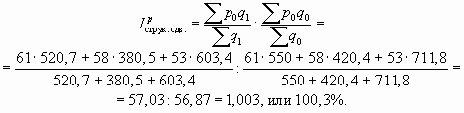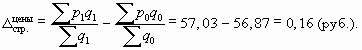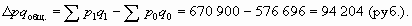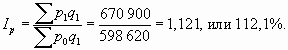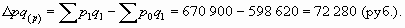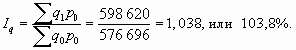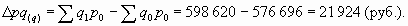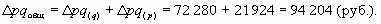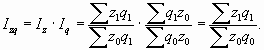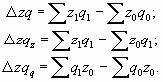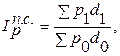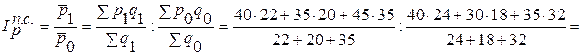что такое индекс структурных сдвигов

Электронная библиотека

При изучении качественных показателей часто приходится рассматривать изменение во времени (пространстве) средней величины индексируемого показателя для определенной однородной совокупности.

Средняя величина является сводной характеристикой качественного показателя и складывается под влиянием значений показателя у индивидуальных элементов (единиц), из которых состоит совокупность и под влиянием их весов (структуры совокупности).

Если любой качественный индексируемый показатель обозначить через х, а его веса через f, то динамику среднего показателя можно отразить как за счет изменения обоих факторов (х и f), так и за счет каждого фактора отдельно. В результате получим три различных индекса: индекс переменного состава, индекс фиксированного (постоянного) состава и индекс структурных сдвигов.

Индекс переменного состава – отражает динамику среднего показателя за счет изменения индексируемой величины х у отдельных элементов (частей целого) и за счет изменения весов f, по которым взвешиваются отдельные значения х.

Любой индекс переменного состава – это отношение двух средних величин для однородной совокупности (за два периода или по двум территориям):

Индекс фиксированного (постоянного) состава – отражает динамику среднего показателя лишь за счет изменения индексируемой величины х, при фиксировании весов на уровне, как правило, отчетного периода f₁:

Например, изменение цены на отдельных рынках (предприятиях) можно выявить с помощью индекса фиксированного (постоянного) состава:

Индекс постоянного состава показывает изменение средней цены за счет изменения индивидуальных цен.

Индекс структурных сдвигов – показывает динамику среднего показателя лишь за счет изменения весов f при фиксировании индексируемой величины на уровне базисного периода х₀.

Например, влияние на изменение средних цен за счет структуры покажет индекс структурных сдвигов:

Индекс структурных сдвигов показывает изменение средней цены за счет изменения структуры продаж, производства.

Между вышеперечисленными индексами существует взаимосвязь: индекс переменного состава есть произведение индекса постоянного состава на индекс структурных сдвигов:

Рассмотрим расчет индексов на конкретном примере.

Источник

Что такое индекс структурных сдвигов

юФПВЩ ТБУУЮЙФБФШ ЙОДЕЛУ ГЕО РЕТЕНЕООПЗП УПУФБЧБ УОБЮБМБ ПРТЕДЕМЙН УТЕДОАА ГЕОХ ФПЧБТБ н Ч ПФЮЕФОПН Й ВБЪЙУОПН РЕТЙПДБИ:

фПЗДБ РП ЖПТНХМЕ (8.9)

ЙМЙ 118%

уТЕДОСС ГЕОБ ОБ ФПЧБТ н ОБ ТЩОЛБИ ЗПТПДБ Ч НБТФЕ РП УТБЧОЕОЙА У СОЧБТЕН ХЧЕМЙЮЙМБУШ ОБ 18%.

оБ ЙЪНЕОЕОЙЕ УТЕДОЕЗП ХТПЧОС РПЛБЪБФЕМС ЧУЕЗДБ ПЛБЪЩЧБАФ ЧМЙСОЙЕ ДЧБ ЖБЛФПТБ: ЙЪНЕОЕОЙЕ ЪОБЮЕОЙС ЙОДЕЛУЙТХЕНПЗП РПЛБЪБФЕМС Х ПФДЕМШОЩИ ЕДЙОЙГ УПЧПЛХРОПУФЙ Й ЙЪНЕОЕОЙЕ УФТХЛФХТЩ УПЧПЛХРОПУФЙ (ЧЕУПЧ).

юФПВЩ ЙЪНЕТЙФШ ЧМЙСОЙЕ ОБ ДЙОБНЙЛХ УТЕДОЕЗП ХТПЧОС РПЛБЪБФЕМС ЛБЦДПЗП ЙЪ ЬФЙИ ЖБЛФПТПЧ ЙУЮЙУМСАФ ЙОДЕЛУ РПУФПСООПЗП (ЖЙЛУЙТПЧБООПЗП) УПУФБЧБ Й ЙОДЕЛУ УФТХЛФХТОЩИ УДЧЙЗПЧ.

ч ПВЭЕН ЧЙДЕ ПО НПЦЕФ ВЩФШ ЪБРЙУБО УМЕДХАЭЙН ПВТБЪПН:

,

(8.10)

рТЙНЕОЙФЕМШОП Л ДБООЩН ФБВМ. 8.6. ПРТЕДЕМЙН ЙОДЕЛУ РПУФПСООПЗП УПУФБЧБ

ЙМЙ 116,8%

фБЛЙН ПВТБЪПН, ГЕОБ Ч НБТФЕ РП УТБЧОЕОЙА У СОЧБТЕН ЧПЪТПУМБ Ч УТЕДОЕН ОБ 116.8%.

пО ТБУУЮЙФЩЧБЕФУС РП ЖПТНХМЕ:

(8.11)

чЩЮЙУМЙН ЧМЙСОЙЕ ЙЪНЕОЕОЙС УФТХЛФХТЩ ОБ ДЙОБНЙЛХ УТЕДОЕК ГЕОЩ ОБ РТЙНЕТЕ ДБООЩИ ФБВМЙГЩ 8.6.

ЙМЙ 101,1%

йЪНЕОЕОЙЕ ДПМЙ ТЩОЛПЧ Ч ПВЭЕН ПВЯЕНЕ ТЕБМЙЪБГЙЙ ФПЧБТБ РТЙЧЕМП Л ТПУФХ УТЕДОЕК ГЕОЩ ОБ 1,1%.

йОДЕЛУЩ РЕТЕНЕООПЗП, РПУФПСООПЗП УПУФБЧБ Й УФТХЛФХТОЩИ УДЧЙЗПЧ ЧЪБЙНПУЧСЪБОЩ УМЕДХАЭЙН ПВТБЪПН:

ч ТБУУНПФТЕООПН РТЙНЕТЕ

бОБМПЗЙЮОП УФТПСФУС УЙУФЕНЩ ЙОДЕЛУПЧ ДМС ДТХЗЙИ РПЛБЪБФЕМЕК.

Источник

Индексы в статистике

10.5. Анализ динамики среднего уровня показателя

Относительное изменение среднего уровня качественного показателя характеризуется с помощью системы индексов переменного, постоянного состава и индекса структурных сдвигов, позволяющих оценить влияние каждого фактора на его динамику.

Индекс постоянного (фиксированного) состава показывает, как в среднем изменилось значение качественного показателя у единиц совокупности при одинаковой фиксированной ее структуре. В общем виде его можно записать следующим образом:

Формула индекса влияния структурных сдвигов, представляющего собой отношение средних величин рассматриваемого качественного показателя, рассчитанных при структуре совокупности отчетного и базисного периодов при базисном уровне качественного показателя, выглядит следующим образом:

Поскольку индекс переменного состава показывает изменение исследуемого явления за счет всех факторов, то между индексами существует следующая взаимосвязь:

.

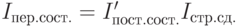
Так, при изучении изменения средней цены товара (например, продаваемого в разных регионах) индекс переменного состава можно записать следующим образом:

Подставляя вместо P₀ и P₁ выражения для расчета средних уровней цен товара отчетного и базисного периодов, получим его развернутую формулу

На его величину оказывают влияние два фактора: изменение цены товара в каждом регионе и структуры продаж. Абсолютное изменение среднего уровня цены товара за счет двух факторов покажет разность между числителем и знаменателем рассматриваемого индекса:

Индекс цен постоянного (фиксированного) состава показывает изменение средней цены товара только за счет изменений цен в каждом регионе. Индекс цен постоянного состава имеет вид

Абсолютное изменение среднего уровня цены за счет изменения индексируемой величины покажет разность между числителем и знаменателем данного индекса

Индекс структурных сдвигов позволяет оценить влияние на формирование среднего уровня цены изменений в структуре продаж товара:

Абсолютное изменение среднего уровня качественного показателя (в данном случае средней цены) за счет структурных сдвигов

Пример 10.6. В таблице приведены цены и объемы продаж товара «А» в трех регионах.

Таблица 10.4.

Регион	Цена товара «А», руб. за кг		Объем продаж товара «А», тыс. кг
	базисный период, p0	отчетный период, p1	базисный период, q0	отчетный период, q1
I	61	69	550,0	520,7
II	58	65	420,4	380,5
III	53	57	711,8	603,4

Индекс цен переменного состава равен

Общее измерение средней цены в абсолютном выражении

За счет действия двух факторов средняя цена увеличилась на 11,1%, или на 6,31 руб.

Для определения влияния первого фактора (цен в каждом регионе) на динамику средней цены исчислим индекс цен постоянного состава:

Тогда влияние первого фактора в абсолютном выражении можно определить как

Таким образом, в результате изменения цен товара «А» в отдельных регионах его средняя цена увеличилась на 10,8%, или на 6,15 руб.

Влияние на анализируемый показатель структурных изменений в структуре продаж товара «А» покажет индекс структурных сдвигов

В абсолютном выражении

В результате изменения структуры продаж товаров по регионам средняя цена возросла на 0,3%, или 16 копеек.

Проверим взаимосвязь индексов и абсолютных приростов:

10.6. Факторный анализ

Покажем это по данным примера 10.2 о ценах и объеме продаж молочной продукции (см. табл. в примере).

Пример 10.7. Проанализируем прирост товарооборота под влиянием двух факторов: изменения цен на товары и объема их продаж. Общий индекс товарооборота равен

Как видим, товарооборот возрос на 94 204 руб. (или 16,3%) за счет двух факторов.

Общий индекс цен, как отмечалось выше, показывает относительное изменение товарооборота под влиянием цен:

Разность между числителем и знаменателем этого индекса позволяет оценить влияние цен на динамику товарооборота в абсолютном выражении:

Таким образом, за счет роста цен на молочную продукцию товарооборот увеличился на 72 280 руб., или на 12,1%.

Абсолютный прирост товарооборота за счет изменения объема продаж молочной продукции определим как разность между числителем и знаменателем этого индекса

Произведение индексов цен и физического объема товарооборота равно общему индексу товарооборота:

l_pq= l_p x l_q = 1,121 * 1,038 = 1,163 или 116,3%

Если сложить абсолютные изменения товарооборота за счет первого и второго фактора, то получим его общее абсолютное изменение:

Аналогично проводится анализ изменения затрат на производство продукции под воздействием двух факторов: изменения себестоимости продукции и объемов производства. Относительное влияние отражают индексы

Абсолютное изменение затрат на производство за счет отдельных факторов рассчитывается следующим образом:

Взаимосвязь абсолютных изменений определяется уравнением

Источник

Индексы переменного и постоянного состава, индекс структурных сдвигов

Для изучения динамики качественных показателей (цена, себестоимость, производительность труда, средняя заработная плата и т. д.) определяют изменение средней величины индексируемого показателя, которое обусловлено взаимодействием двух факторов:

· изменение значения индексируемого показателя у отдельных групп единиц;

· изменение структуры явления.

Для определения влияния каждого из этих факторов на общую динамику средней применяются индексы переменного, постоянного (фиксированного) состава и индекс структурных сдвигов.

Индексом переменного состава является индекс, отражающий соотношение средних уровней изучаемого явления, относящихся к разным периодам.

Рассмотрим индекс цен переменного состава:

.

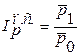
Отражает соотношение средней цены товаров в текущем и базисном периодах.

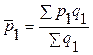
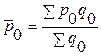
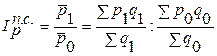
Поскольку средняя цена товаров определяется по формуле средней арифметической взвешенной как отношение товарооборота к объему продаж (,), то индекс цен переменного состава может быть записан следующим образом:

.

Если от объемов товара в натуральном выражении перейти к их удельным весам, то данный индекс может быть записан так:

где 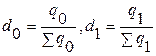– доля каждого товара соответственно в базисном и отчетном периодах.

Индекс постоянного (фиксированного) состава – характеризует динамику средней величины при одной и той же фиксированной структуре. Индекс постоянного состава показывает, как в отчетном периоде по сравнению с базисным изменилось среднее значение показателя по какой-либо однородной совокупности за счет изменения только самой индексируемой величины, т. е. когда влияние структурного фактора устранено.

Индекс цен фиксированного состава:

или – индекс цен фиксированного состава.

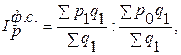
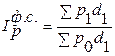
Индексом структурных сдвигов называется индекс, характеризующий влияние изменения структуры изучаемого явления на динамику среднего уровня изучаемого явления.

Индекс цен структурных сдвигов:

или – индекс цен структурных сдвигов.

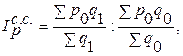
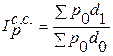
Взаимосвязь: .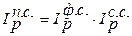

Помимо мультипликативной модели, на основе индексов переменного, постоянного состава и структурных сдвигов может быть построено аддитивное разложение, отражающее абсолютное изменение среднего уровня качественного показателя за счет отдельных факторов.

Так, например, общий абсолютный прирост (уменьшение) средней цены товаров в целом по совокупности находится как разность числителя и знаменателя индекса цен переменного состава:

или .

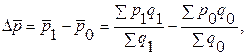
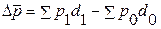
Абсолютный прирост (уменьшение) средней цены за счет изменения цен по отдельным единицам совокупности (например, по отдельным рынкам) определяется как разность числителя и знаменателя индекса цен фиксированного состава:

или .

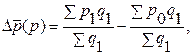
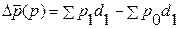
Абсолютный прирост (уменьшение) средней цены за счет структурных изменений рассчитывается как разность числителя и знаменателя индекса цен структурных сдвигов:

или .

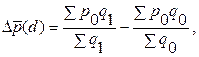
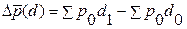
Общий прирост результативного показателя должен быть равен сумме приростов за счет каждого из факторов. Аддитивное разложение имеет вид:

.

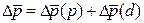
Пример 2: Имеются следующие данные о продаже картофеля на рынках города:

Данные о продаже картофеля на рынках города

Рынок	Базисный период	Отчетный период
Цена за 1 кг, руб.	Продано, ц	Цена за 1 кг, руб.	Продано, ц

Определить индекс цен переменного состава, индекс цен фиксированного состава и индекс цен структурных сдвигов. Сделать выводы по результатам расчетов.

1) Индекс цен переменного состава:

, таким образом, в отчетном периоде по сравнению с базисным средняя цена картофеля по рынкам города увеличилась на 15,8 %;

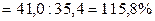
2) Индекс цен фиксированного состава:

– за счет изменения цен на картофель на отдельных рынках средняя цена в отчетном периоде по сравнению с базисным увеличилась на 16,8 %;

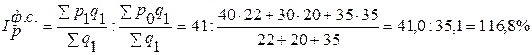
3) Индекс цен структурных сдвигов:

, то есть за счет изменения долей отдельных рынков в их общем объеме продаж (или за счет структурных сдвигов) в отчетном периоде по сравнению с базисным средняя цена картофеля снизилась на 0,8%.

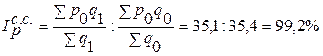
Пример 3: Продукт А производится на двух предприятиях региона:

Данные о себестоимости и физическом объеме выпуска продукта А предприятиями региона

№ предприятия	Себестоимость за единицу продукта, долл. США	Физический объем выпуска, тыс. шт.
Базисный период	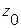Отчетный период	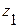Базисный период	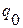Отчетный период

1) изменение средней себестоимости продукта А в процентах и в абсолютном размере;

2) абсолютное изменение средней себестоимости за счет действия отдельных факторов:

а) изменения себестоимости по отдельным предприятиям;

б) структурных сдвигов в общем объеме выпуска продукции.

1) Определим удельные веса каждого предприятия в производстве продукта А в отчетном и базисном периодах:

№ предприятия	Физический объем выпуска, тыс. шт.	Удельный вес выпуска, %
Базисный период	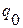Отчетный период	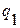Базисный период	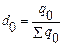Отчетный период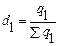
0,308 0,692	0,452 0,548
Итого	1,000	1,000

2) Изменение средней себестоимости в процентах характеризует индекс себестоимости переменного состава:

.

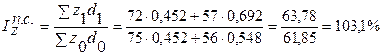
Абсолютное изменение средней себестоимости:

долл. США.

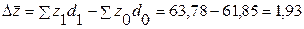
Средняя себестоимость продукта А в отчетном периоде по сравнению с базисным увеличилась на 3,1%, или на 1,93 долл. США;

3) а) Абсолютное изменение средней себестоимости за счет изменения себестоимостей по отдельным предприятиям можно определить, если из числителя индекса фиксированного состава вычесть знаменатель:

долл. США.

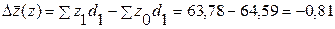
За счет изменения себестоимости продукта А на отдельных предприятиях средняя себестоимость снизилась на 0,81 долл. США;

б) Абсолютное изменение средней себестоимости за счет структурных сдвигов в общем объеме производства можно определить, если из числителя индекса структурных сдвигов вычесть знаменатель:

долл. США.

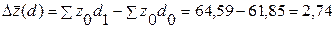
За счет изменения долей отдельных предприятий в производстве продукта А (или за счет структурных сдвигов общем объеме выпуска) его средняя себестоимость увеличилась на 2,74 долл. США.

;

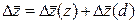
Разновидностью относительных величин является территориальный индекс, т. е. сравнение показателей, относящихся к разным территориям.

Пример: Товарооборот регионов А и В, база сравнения регион В.

, , тогда .

Источник