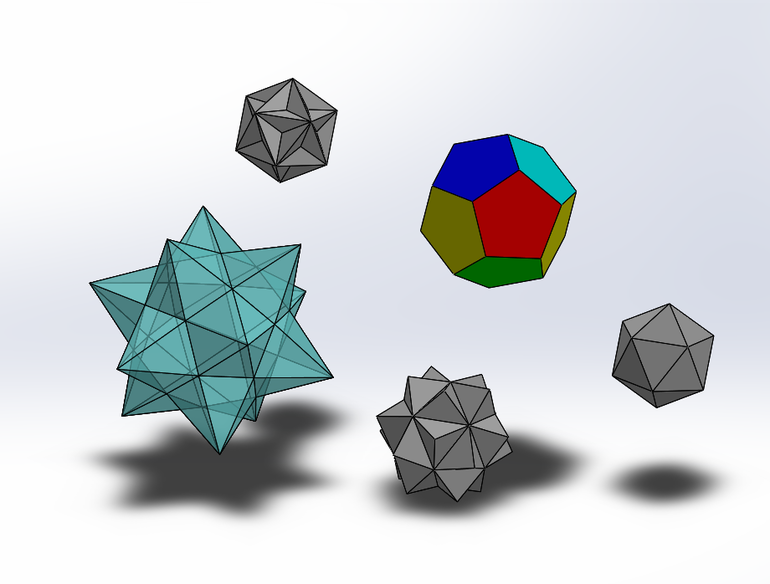
что такое икосаэдрическая система координат
Бумажная модель
Используя 30 квадратных листов бумаги (размер каждой стороны 7,5 см), можно сделать довольно крепкую версию одной из разновидности этого геометрического чуда совсем без склеивания. Если в запасе есть материал разного цвета, то получится яркий и красивый макет с разноцветными блоками. Инструкция по изготовлению звездчатого икосаэдра поэтапно:
Всего таких блоков нужно сделать 30. Например, по 10 разного цвета.
Сборка элементов
Теперь самое время собирать блоки вместе. Поверхность звездчатого икосаэдра состоит из нескольких пирамид. Чтобы было проще, нужно представить этот сложный куб, над которым идёт работа, в виде единственного додекаэдра (12-гранный правильный пятиугольник — ещё одно тело Платона), где каждая из его двадцати вершин будет заменена пирамидой. Все 30 единиц пойдут на формирование этих 20 пирамид. Ход работы по сборке икосаэдра. Схема поэтапно:
В итоге получится красивая объёмная фигура, а если она сделана из цветной бумаги, то ещё и красочная. Безусловно, если нужно сэкономить время и силы, можно сильно упростить задачу и найти готовый шаблон модели, распечатать развёртку икосаэдра на бумаге и вырезать, оставляя припуски, а затем склеить.
Основные виды
Вообще, эта геометрическая фигура — одно из платоновых тел, известных с древних времён. Их всего пять: тетраэдр, куб, октаэдр, додекаэдр и икосаэдр. Их определение довольно простое: все они представляют собой многогранники, состоящие из конгруэнтных (одинаковых по форме и размеру) регулярных (все углы равны, как и все стороны) полигональных граней, встречающихся в каждой вершине.
Обычный икосаэдр представлен в двух основных видах, обладающих одинаковыми признаками. У каждого есть 30 рёбер и 20 равносторонних треугольных граней, которые собираются по 5 штук, образуя 12 вершин. Оба имеют икосаэдрическую симметрию, центром которой является точка пересечения всех осевых линий, и называются:
Звездчатые формы образуются, когда грани или края многогранника расширяют до тех пор, пока они не встретятся, чтобы сформировать новую фигуру. Это делается таким образом, что сохраняются центр,оси и плоскости симметрии родительской фигуры. К слову, большой икосаэдр можно отнести к этому виду. У других «звёздочек» есть более одной грани в каждой плоскости или они образуют соединения более простых многогранников. Это не строго икосаэдры, но их часто так называют. В таблице представлены несколько разновидностей звездчатых тел.
У него 12 правильных пятиугольных граней, 20 правильных шестиугольных граней, 60 вершин и 90 ребер.
СОДЕРЖАНИЕ
Строительство
Характеристики
Декартовы координаты
Декартовы координаты вершин усеченного икосаэдра с центром в начале координат представляют собой четные перестановки :
Ортогональные проекции
| В центре | Вершина | Край 5-6 | Край 6-6 | Лицо шестиугольника | Лицо Пентагона |
|---|---|---|---|---|---|
| Твердый |  |  |  | ||
| Каркас |  | 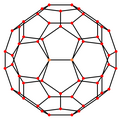 |  |  |  |
| Проективная симметрия | [2] | [2] | [2] | [6] | [10] |
| Двойной | 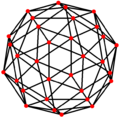 | 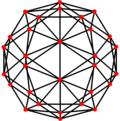 |  |  |  |
Сферическая черепица
Габаритные размеры
р ты знак равно а 2 1 + 9 φ 2 знак равно а 4 58 + 18 5 ≈ 2,478 018 66 а <\ displaystyle r _ <\ mathrm > = <\ frac <2>> <\ sqrt <1 + 9 \ varphi ^ <2>>> = <\ frac <4>> <\ sqrt <58 + 18 <\ sqrt <5>>>> \ приблизительно 2.478 \, 018 \, 66a>
Этот результат легко получить, используя один из трех ортогональных золотых прямоугольников, нарисованных в исходном икосаэдре (до отсечения), в качестве отправной точки для наших размышлений. Угол между сегментами, соединяющими центр, и вершинами, соединенными общим ребром (рассчитанный на основе этой конструкции), составляет примерно 23,281446 °.
Площадь и объем
Площадь A и объем V усеченного икосаэдра с длиной ребра a равны:
С единичными краями площадь поверхности составляет (округленная) 21 для пятиугольников и 52 для шестиугольников, вместе 73 (см. Площади правильных многоугольников ).
Усеченный икосаэдр легко демонстрирует эйлерову характеристику :
Приложения
Мячи, используемые в ассоциативном футболе и командном гандболе, являются, пожалуй, самым известным примером сферического многогранника, аналога усеченного икосаэдра, встречающегося в повседневной жизни. Мяч состоит из правильных пятиугольников и шестиугольников, но он более сферический из-за давления воздуха внутри и эластичности шара. Этот тип мяча был представлен на чемпионате мира в 1970 году (начиная с 2006 года этот знаковый дизайн был заменен альтернативными узорами ).
В популярной культуре ремесел большие шары-искры могут быть сделаны с использованием рисунка икосаэдра и пластиковых, пенополистирольных или бумажных стаканчиков.
В искусстве
Название происходит от Греческий εἴκοσι (eíkosi) «двадцать» и ἕδρα (Хедра) ‘сиденье’. Множественное число может быть «икосаэдрами» или «икосаэдрами» ( /- d р ə / ).
Содержание
Размеры
Если длина ребра правильного икосаэдра равна а, то радиус ограниченного сфера (тот, который касается икосаэдра во всех вершинах)
и радиус вписанной сферы (касательная каждой грани икосаэдра)
в то время как средний радиус, который касается середины каждого края, равен
Площадь и объем
Площадь поверхности А и объем V правильного икосаэдра с реберной длиной а находятся:
Последний F = 20 раз больше объема генерала тетраэдр с вершиной в центре вписанной сферы, где объем тетраэдра в три раза больше площади основания √ 3 а 2 / 4 раз больше его высоты ря.
Коэффициент заполнения объема описанной сферы составляет:
Сфера, вписанная в икосаэдр, будет охватывать 89,635% его объема по сравнению с 75,47% для додекаэдра.
Средняя часть икосаэдра будет иметь объем в 1,01664 раза больше объема икосаэдра, что на сегодняшний день является наиболее близким по объему подобием любого платонового тела с его средней сферой. Возможно, это делает икосаэдр самым «круглым» из платоновых тел.
Декартовы координаты
Вершины икосаэдра с центром в начале координат с длиной ребра 2 и по окружности из ϕ + 2 ≈ 1.9 
Взятие всех перестановок (не только циклических) приводит к Соединение двух икосаэдров.
Обратите внимание, что эти вершины образуют пять наборов из трех концентрических, взаимно ортогональный золотые прямоугольники, ребра которого образуют Кольца Борромео.
Если исходный икосаэдр имеет длину ребра 1, его двойственный додекаэдр имеет длину края √ 5 − 1 / 2 = 1 / ϕ = ϕ − 1.
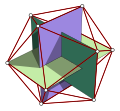
12 граней обычного октаэдр можно разделить в золотом сечении так, чтобы полученные вершины определяли правильный икосаэдр. Это делается путем размещения векторов по краям октаэдра таким образом, чтобы каждая грань была ограничена циклом, а затем аналогичным образом разделяя каждое ребро на золотую середину в направлении его вектора. В пять октаэдров определение любого данного икосаэдра в виде регулярного полиэдрическое соединение, в то время как два икосаэдра который может быть определен таким образом из любого данного октаэдра, образующего однородное соединение многогранника.
Сферические координаты
Расположение вершин правильного икосаэдра можно описать с помощью сферические координаты, например как широта и долгота. Если две вершины взяты на северном и южном полюсах (широта ± 90 °), то остальные десять вершин находятся на широте ±арктан( 1 / 2 ) ≈ ± 26,57 °. Эти десять вершин находятся на равном расстоянии друг от друга по долготе (36 ° друг от друга), чередуя северную и южную широты.
Эта схема использует тот факт, что правильный икосаэдр имеет пятиугольную форму. гиродлинная бипирамида, с D5d двугранная симметрия- то есть он состоит из двух конгруэнтных пятиугольных пирамид, соединенных пятиугольной антипризма.
Ортогональные проекции
Икосаэдр имеет три особых ортогональные проекциис центром на грани, ребре и вершине:
| В центре | Лицо | Край | Вершина |
|---|---|---|---|
| Самолет Кокстера | А2 | А3 | ЧАС3 |
| График |  |  |  |
| Проективный симметрия | [6] | [2] | [10] |
| График |  Лицо нормальное |  Край нормальный |  Вершина нормальная |
Сферическая черепица
Икосаэдр также можно представить в виде сферическая черепица, и проецируется на плоскость через стереографическая проекция. Эта проекция конформный, сохраняя углы, но не площади или длины. Прямые линии на сфере проецируются как дуги окружности на плоскость.
Другие факты
Строительство по системе равносторонних линий
 Икосаэдр ЧАС3 Самолет Кокстера |  6-ортоплекс D6 Самолет Кокстера |
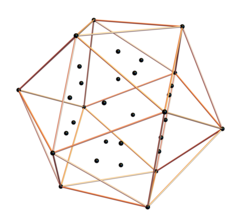
Геометрически эту конструкцию можно представить как 12 вершин 6-ортоплекс проецируется на 3 измерения. Это представляет собой геометрическая складка D6 к H3 Группы Кокстера: 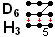 | |
Видно этими 2D Самолет Кокстера В ортогональных проекциях две перекрывающиеся центральные вершины определяют третью ось в этом отображении.
Следующая конструкция икосаэдра позволяет избежать утомительных вычислений в числовое поле ℚ [ √ 5 ] необходимо в более элементарных подходах.
Чтобы построить такую равностороннюю систему, мы начнем с этого квадрата 6 × 6 матрица:
Вторая простая конструкция икосаэдра использует теория представлений из переменная группа А5 действуя прямым изометрии на икосаэдре.
Симметрия
Вращательный группа симметрии правильного икосаэдра изоморфный к переменная группа на пять букв. Этот не-абелевский простая группа единственный нетривиальный нормальная подгруппа из симметричная группа на пять букв. Поскольку Группа Галуа генерального уравнение пятой степени изоморфна симметрической группе на пяти буквах, и эта нормальная подгруппа проста и неабелева, общее уравнение квинтики не имеет решения в радикалах. Доказательство Теорема Абеля – Руффини использует этот простой факт, и Феликс Кляйн написал книгу, в которой использовала теорию симметрий икосаэдра для получения аналитического решения общего уравнения пятой степени (Кляйн 1884). Видеть симметрия икосаэдра: связанные геометрии для дальнейшей истории и связанных симметрий семи и одиннадцати букв.
Полная группа симметрии икосаэдра (включая отражения) известна как полная группа икосаэдра, и изоморфна произведению группы вращательной симметрии и группы C2 размером два, который создается отражением через центр икосаэдра.
Звёздчатые
 Грани икосаэдра вытянуты наружу при пересечении плоскостей, определяя области в пространстве, как показано этим звездчатая диаграмма пересечений в единой плоскости. |  |  |  |  |  |  |  |
 |  |  |  |  |  |  | |
 |  |  |  |  |  |  |
Грани
В малый звездчатый додекаэдр, большой додекаэдр, и большой икосаэдр три огранки правильного икосаэдра. Они разделяют то же самое расположение вершин. У всех 30 ребер. Правильный икосаэдр и большой додекаэдр имеют общие черты. расположение кромок но различаются гранями (треугольники против пятиугольников), как и малый звездчатый додекаэдр и большой икосаэдр (пентаграммы против треугольников).
| Выпуклый | Обычные звезды | ||
|---|---|---|---|
| икосаэдр | большой додекаэдр | малый звездчатый додекаэдр | большой икосаэдр |
 |  |  |  |
Геометрические отношения
Имеются искажения икосаэдра, которые, хотя и не являются регулярными, тем не менее вершинно-однородный. Это инвариантный под тем же вращения как тетраэдр, и в некоторой степени аналогичны курносый куб и курносый додекаэдр, включая некоторые формы, которые хиральный и некоторые с Tчас-симметрия, т.е. имеют разные плоскости симметрии от тетраэдра.
Икосаэдр уникален среди Платоновы тела в обладании двугранный угол не менее 120 °. Его двугранный угол составляет примерно 138,19 °. Таким образом, точно так же, как шестиугольники имеют углы не менее 120 ° и не могут использоваться в качестве граней выпуклого правильного многогранника, поскольку такая конструкция не удовлетворяет требованию, чтобы по крайней мере три грани пересекались в вершине и оставляли положительный дефект для трехмерного складывания икосаэдры нельзя использовать в качестве клетки выпуклой регулярной полихорон потому что, аналогично, по крайней мере три ячейки должны встретиться на краю и оставить положительный дефект для складывания в четырех измерениях (как правило, для выпуклого многогранник в п размеры, не менее трех грани должен встретиться на вершина горы и оставить положительный дефект для складывания п-Космос). Однако в сочетании с подходящими ячейками, имеющими меньшие двугранные углы, икосаэдры могут использоваться в качестве ячеек в полурегулярных полихорах (например, курносый 24-элементный), точно так же, как шестиугольники могут использоваться как грани в полуправильных многогранниках (например, усеченный икосаэдр). Наконец, невыпуклые многогранники не предъявляют таких же строгих требований, как выпуклые многогранники, и икосаэдры действительно являются клетками многогранников. икосаэдрический 120-элементный, один из десяти невыпуклая правильная полихора.
Икосаэдр также можно назвать гиродлинная пятиугольная бипирамида. Его можно разложить на гировидная пятиугольная пирамида и пятиугольная пирамида или в пятиугольная антипризма и две равные пятиугольные пирамиды.
Связь с 6-кубом и ромбическим триаконтаэдром
Используемые базисные векторы трехмерной проекции [u, v, w]:
Равномерная окраска и подсимметрия
Есть 3 равномерные раскраски икосаэдра. Эти раскраски можно представить как 11213, 11212, 11111, назвав 5 треугольных граней вокруг каждой вершины их цветом.
Икосаэдр можно рассматривать как курносый тетраэдр, так как пренебрежение правильного тетраэдра дает правильный икосаэдр с хиральной тетраэдрическая симметрия. Он также может быть построен как чередующийся усеченный октаэдр, имеющий пиритоэдрическая симметрия. Вариант пиритоэдрической симметрии иногда называют псевдоикосаэдр, и двойственен пиритоэдр.
Использование и естественные формы
Биология
Обнаружены также различные бактериальные органеллы икосаэдрической формы. [11] Икосаэдрическая оболочка, инкапсулирующая ферменты и лабильные промежуточные соединения, построена из различных типов белков с BMC домены.
В 1904 г. Эрнст Геккель описал ряд видов Радиолярии, включая Икосаэдры Circogonia, скелет которого имеет форму правильного икосаэдра. Копия иллюстрации Геккеля к этому радиолярию приводится в статье о правильные многогранники.
Химия
В близко-карбораны представляют собой химические соединения, форма которых очень близка к икосаэдру. Икосаэдр побратимство также встречается в кристаллах, особенно наночастицы.
Много бориды и аллотропы бора содержат бор B12 икосаэдр как элемент базовой конструкции.
Игрушки и игры
Икосаэдр игральная кость с двадцати сторон использовались с древних времен. [12]
В нескольких ролевые игры, Такие как Подземелья и Драконы, двадцатигранный кубик (d20 для краткости) обычно используется для определения успеха или неудачи действия. Этот кубик имеет форму правильного икосаэдра. Он может быть дважды пронумерован от «0» до «9» (в какой форме он обычно используется как десятигранный кубик или d10), но большинство современных версий имеют маркировку от «1» до «20».
В настольной игре используется икосаэдр Scattergories выбрать букву алфавита. Шесть букв опущены (Q, U, V, X, Y и Z).
Внутри Волшебный шар 8, различные ответы на Да, без вопросов начертаны на правильном икосаэдре.
Другие
Р. Бакминстер Фуллер и японский картограф Сёдзи Садао [13] разработал карту мира в виде развернутого икосаэдра, названного Полная проекция, максимальная искажение составляет всего 2%. Американец электронная музыка дуэт ODESZA использовать в качестве логотипа обычный икосаэдр.
Икосаэдрический граф
Высокая степень симметрии многоугольника воспроизводится в свойствах этого графа, который дистанционно-транзитивный и симметричный. В группа автоморфизмов имеет порядок 120. Вершины могут быть цветной с 4 цветами, края с 5 цветами и диаметр равно 3. [14]
Граф икосаэдра Гамильтониан: есть цикл, содержащий все вершины. Это также планарный граф.
Уменьшенные правильные икосаэдры
Есть 4 связанных Твердые тела Джонсона, включая пятиугольные грани с подмножеством из 12 вершин. Подобный правильный икосаэдр в разрезе имеет 2 соседние вершины, уменьшенные, оставляя две трапециевидные грани, а у бифастигиума 2 противоположных набора удаленных вершин и 4 трапециевидных грани. Пятиугольная антипризма образована удалением двух противоположных вершин.
Связанные многогранники и многогранники
Икосаэдр можно преобразовать усечение последовательность в его двойной, додекаэдр:
Как плоскостный тетраэдр и чередование усеченного октаэдра, он также существует в семействах тетраэдрической и октаэдрической симметрии:
Этот многогранник топологически связан как часть последовательности правильных многогранников с Символы Шлефли <3,п>, переходя в гиперболическая плоскость.
| *п32 изменения симметрии правильных мозаик: <3,п> | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Сферический | Евклид. | Компактный гипер. | Paraco. | Некомпактный гиперболический | |||||||
 |  |  |  |  |  |  |  |  |  |  |  |
| 3.3 | 3 3 | 3 4 | 3 5 | 3 6 | 3 7 | 3 8 | 3 ∞ | 3 12i | 3 9i | 3 6i | 3 3i |
Правильный икосаэдр, рассматриваемый как курносый тетраэдр, является членом последовательности пренебрежительно многогранники и мозаики с вершинной фигурой (3.3.3.3.п) и Диаграмма Кокстера – Дынкина 

| п32 мутации симметрии курносых плиток: 3.3.3.3.n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Симметрия п32 | Сферический | Евклидово | Компактный гиперболический | Paracomp. | ||||
| 232 | 332 | 432 | 532 | 632 | 732 | 832 | ∞32 | |
| Курносый цифры |  |  |  |  |  |  |  |  |
| Конфиг. | 3.3.3.3.2 | 3.3.3.3.3 | 3.3.3.3.4 | 3.3.3.3.5 | 3.3.3.3.6 | 3.3.3.3.7 | 3.3.3.3.8 | 3.3.3.3.∞ |
| Гироскоп цифры |  |  |  |  |  |  |  |  |
| Конфиг. | V3.3.3.3.2 | V3.3.3.3.3 | V3.3.3.3.4 | V3.3.3.3.5 | V3.3.3.3.6 | V3.3.3.3.7 | V3.3.3.3.8 | V3.3.3.3.∞ |