что такое граф рисунок
Графы: основы теории, алгоритмы поиска
Возможно, вы уже знакомы с понятием спортивного программирования и знаете, что оно помогает развить навыки решения проблем и прокачать технические знания о структурах данных и алгоритмах.
Одной из важнейших составляющих спортивного программирования является изучение алгоритмов. В этой статье мы охватим большое количество алгоритмов, в том числе все алгоритмы на графах, знание которых понадобится вам для успешного решения задач из теории графов на соревнованиях по программированию. Конечно, одних теоретических знаний алгоритмов недостаточно, и вам придётся набить руку в решении практических задач на таких сайтах, как Codeforces. Настоящая же статья представит вам инструменты, необходимые для освоения важных графовых алгоритмов. Итак, приступим.
Что такое граф?
Графы, в понимании программистов, — это не те графики, которые мы изучали в школе. Это не столбиковые диаграммы или гистограммы.
С точки зрения компьютерных наук и дискретной математики, графы — это абстрактный способ представления типов отношений, например дорог, соединяющих города, и других видов сетей. Графы состоят из рёбер и вершин. Вершина — это точка на графе, а ребро — это то, что соединяет две точки на графе.
В условиях задач из теории графов на соревнованиях по программированию обычно говорится о таких вещах, как сети и решётки.
Вот список всех терминов, относящихся к теории графов, которые вам нужно знать:
Представление графов в коде
Для того, чтобы использовать алгоритмы на графах в коде, сначала нам нужно разобраться, как осуществляется представление графов в коде. Весь следующий код будет на C++, так как для спортивного программирования я предпочитаю именно этот язык за его скорость и встроенные функции, позволяющие упростить написание решений задач.
Будут показаны два способа представления графов: матрицы смежности и списки смежности. Больше вам пригодится представление графов в виде списка смежности.
Матрицы смежности
Матрица смежности представляет собой граф в виде двумерной матрицы с размерами V x V, где V — количество вершин графа. Матрицы смежности лучше всего применять, когда V² примерно равно E (числу рёбер), то есть когда граф плотный. Запись a_ij обозначает, сколько рёбер соединяют вершину i и вершину j.
Списки смежности
Другой распространенный способ представления графов в коде — списки смежности. Суть в том, что вы создаёте списки соседей для каждой вершины, а затем помещаете все эти списки в другой список. Их лучше всего применять, когда в графе небольшое количество рёбер, то есть когда граф разрежённый. Если у вас взвешенный граф, т.е. каждое ребро графа имеет какой-то вес, то в списке будут содержаться пары для рёбер (сосед, вес).
Поиск в глубину
Теперь, когда мы научились представлять графы в коде, можем приступить к изучению некоторых алгоритмов на графах! Начнём с поиска в глубину (DFS) и завершим поиском в ширину (BFS). Чтобы не загромождать статью, алгоритмы поиска пути не будут здесь рассматриваться (интересующиеся могут ознакомиться с алгоритмом поиска кратчайшего пути Беллмана-Форда).
Поиск в глубину — это один из базовых алгоритмов на графах. Он применяется для поиска расстояния от одной вершины до других вершин в графе. Это алгоритм обхода.
Поиск в глубину помечает каждую вершину в графе одной из двух меток: посещённая или не посещённая. Алгоритм помечает каждую вершину как посещённую, если удаётся избежать циклов. Он работает следующим образом:
Поиск в ширину
Поиск в ширину — ещё один алгоритм обхода графов. Вместе с алгоритмом поиска вглубь он составит большую часть увлекательных соревнований по программированию, по крайней мере, тех из них, что относятся к графам.
Поиск в ширину тоже помещает каждую вершину в графе в одну из двух категорий: посещённых или непосещённых. И цель у обоих алгоритмов одна и та же: помечать каждую вершину в графе как посещённую, если удаётся избежать циклов. Вот как работает алгоритм поиска в ширину:
Как видите, алгоритм поиска в ширину очень похож на алгоритм поиска в глубину. Однако вместо того, чтобы спускаться вниз по ветви графа или дерева, как это делает алгоритм поиска в глубину, алгоритм поиска в ширину проходит каждый уровень.
Заключение
Освоив теоретическую часть, касающуюся двух самых важных алгоритмов обхода на графах, вам остаётся только практиковаться, чтобы использовать эти алгоритмы в соревнованиях по программированию. Я бы порекомендовал для начала Codeforces: решайте задачи, помеченные тегами bfs и dfs с рейтингом до 1400. Когда почувствуете, что справляетесь с ними, увеличьте сложность.
Отработка навыков решения алгоритмических задач, особенно алгоритмов на графах, поможет вам побеждать на соревнованиях по программированию и успешно проходить технические собеседования. Вперёд — к успехам!
Теория графов. Часть третья (Представление графа с помощью матриц смежности, инцидентности и списков смежности)
Все, что познается, имеет число, ибо невозможно ни понять ничего, ни познать без него – Пифагор
Список смежности (инцидентности)
Взвешенный граф (коротко)
Итак, мы умеем задавать граф графическим способом. Но есть еще два способа как можно задавать граф, а точнее представлять его. Для экономии памяти в компьютере граф можно представлять с помощью матриц или с помощью списков.
Матрица является удобной для представления плотных графов, в которых число ребер близко к максимально возможному числу ребер (у полного графа).
Другой способ называется списком. Данный способ больше подходит для более разреженных графов, в котором число ребер намного меньше максимально возможного числа ребер (у полного графа).
Перед чтением материала рекомендуется ознакомится с предыдущей статьей, о смежности и инцидентности, где данные определения подробно разбираются.
Матрица смежности
Но тем кто знает, но чуть забыл, что такое смежность есть краткое определение.
Смежность – понятие, используемое только в отношении двух ребер или в отношении двух вершин: два ребра инцидентные одной вершине, называются смежными; две вершины, инцидентные одному ребру, также называются смежными.
Матрица (назовем ее L) состоит из n строк и n столбцов и поэтому занимает n^2 места.
Каждая ячейка матрицы равна либо 1, либо 0;
Ячейка в позиции L (i, j) равна 1 тогда и только тогда, когда существует ребро (E) между вершинами (V) i и j. Если у нас положение (j, i), то мы также сможем использовать данное правило. Из этого следует, что число единиц в матрице равно удвоенному числу ребер в графе. (если граф неориентированный). Если ребра между вершинами i и j не существует, то ставится 0.
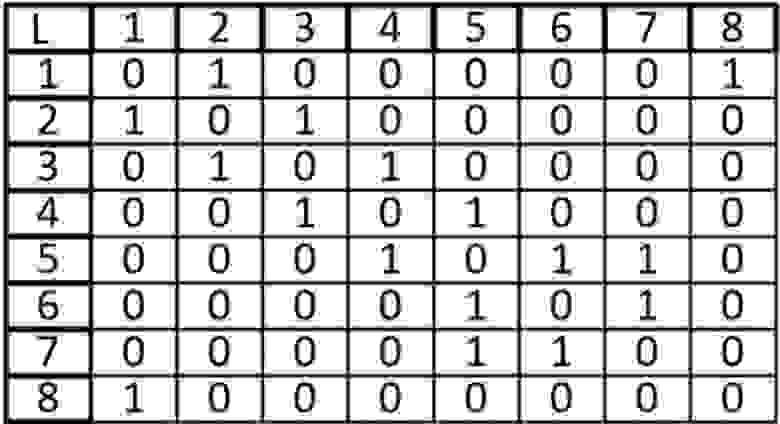
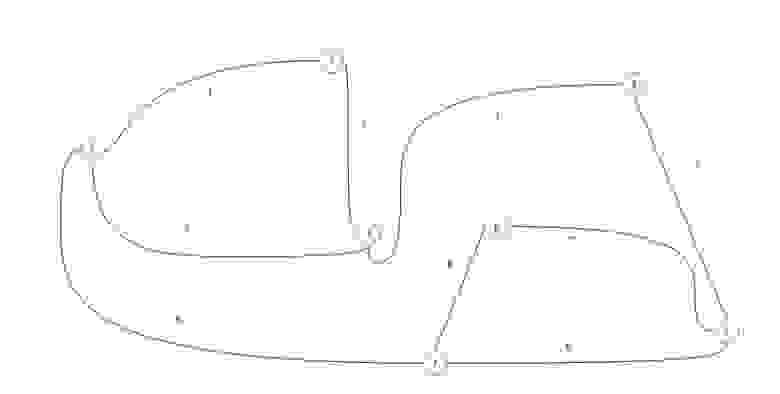
Для практического примера возьмем самый обыкновенный неориентированный граф:
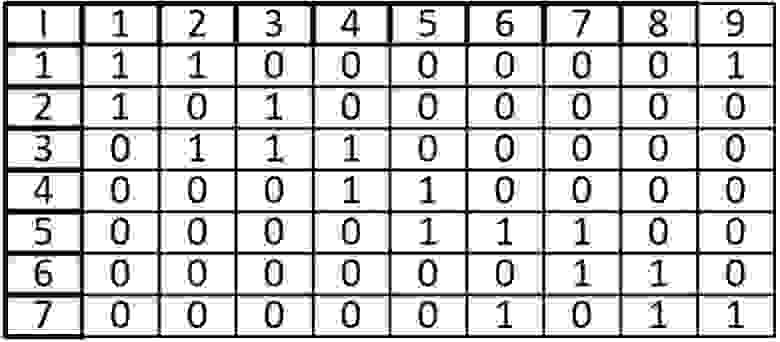
А теперь представим его в виде матрицы:
Ячейки, расположенные на главной диагонали всегда равны нулю, потому что ни у одной вершины нет ребра, которое и начинается, и заканчивается в ней только если мы не используем петли. То есть наша матрица симметрична относительно главной диагонали. Благодаря этому мы можем уменьшить объем памяти, который нам нужен для хранения.
С одной стороны объем памяти будет:
Но используя вышеописанный подход получается:
Потому что нижнюю часть матрицы мы можем создать из верхней половины матрицы. Только при условии того, что у нас главная диагональ должна быть пустой, потому что при наличии петель данное правило не работает.
Если граф неориентированный, то, когда мы просуммируем строку или столбец мы узнаем степень рассматриваемой нами вершины.
Если мы используем ориентированный граф, то кое-что меняется.
Здесь отсутствует дублирование между вершинами, так как если вершина 1 соединена с вершиной 2, наоборот соединена она не может быть, так у нас есть направление у ребра.
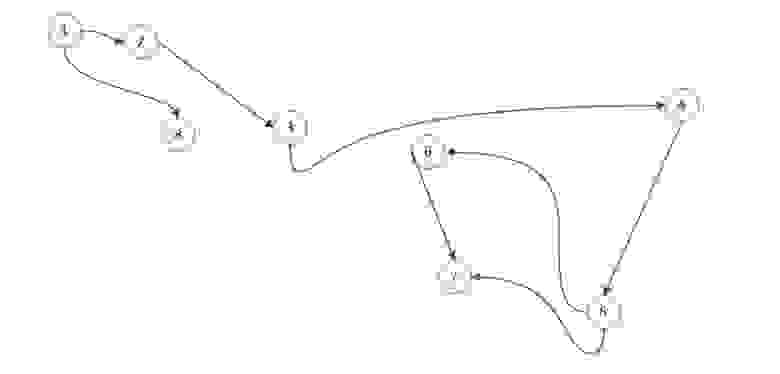
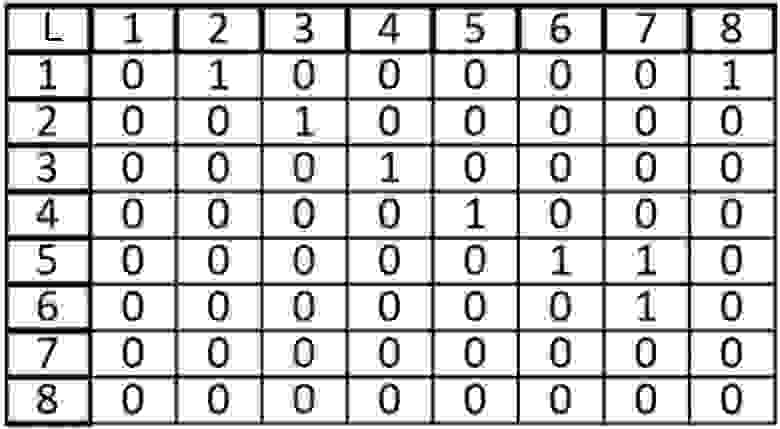
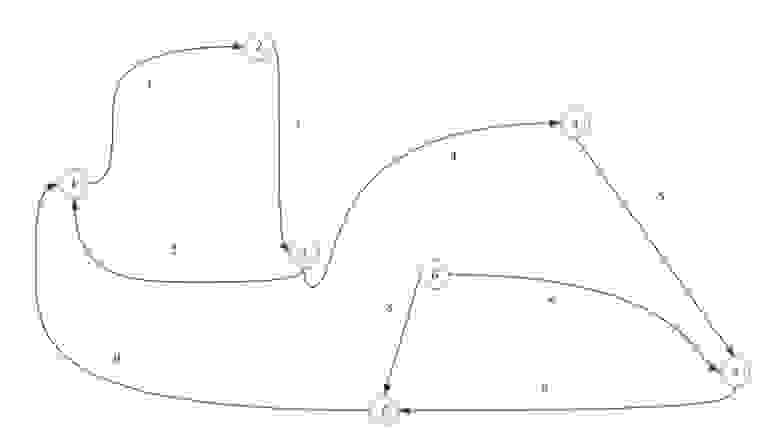
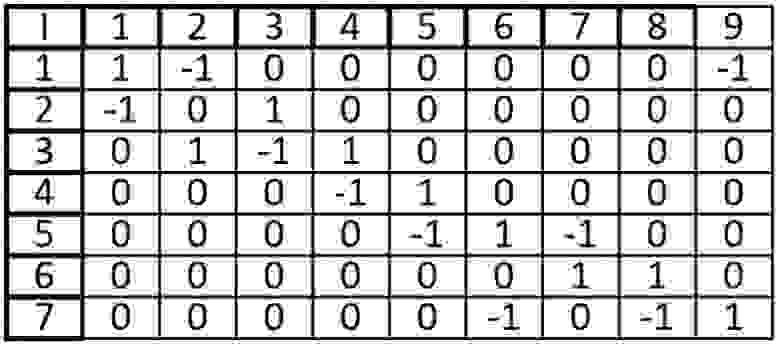
Возьмем в этот раз ориентированный граф и сделаем матрицу смежности для него:
Если мы работаем со строкой матрицы, то мы имеем элемент из которого выходит ребро, в нашем случаи вершина 1 входит в вершину 2 и 8. Когда мы работаем со столбцом то мы рассматриваем те ребра, которые входят в данную вершину. В вершину 1 ничего не входит, значит матрица верна.
Если бы на главной диагонали была бы 1, то есть в графе присутствовала петля, то мы бы работали уже не с простым графом, с каким мы работали до сих пор.
Матрица инцидентности
Инцидентность – понятие, используемое только в отношении ребра и вершины: две вершины (или два ребра) инцидентными быть не могут.
Матрица (назовем ее I) состоит из n строк которое равно числу вершин графа, и m столбцов, которое равно числу ребер. Таким образом полная матрица имеет размерность n x m. То есть она может быть, как квадратной, так и отличной от нее.
Ячейка в позиции I (i, j) равна 1 тогда, когда вершина инцидентна ребру иначе мы записываем в ячейку 0, такой вариант представления верен для неориентированного графа.
Сразу же иллюстрируем данное правило:
Сумма элементов i-ой строки равна степени вершины.
Одной из особенностей данной матрицы является то, что в столбце может быть только две ненулевых ячейки. Так как у ребра два конца.
Список смежности (инцидентности)
Список смежности подразумевает под собой, то что мы работаем с некоторым списком (массивом). В нем указаны вершины нашего графа. И каждый из них имеет ссылку на смежные с ним вершины.
В виде списка это будет выглядеть так:
Неважно в каком порядке вы расположите ссылку так как вы рассматриваете смежность относительно первой ячейки, все остальные ссылки указывают лишь на связь с ней, а не между собой.
Так как здесь рассматривается смежность, то здесь не обойдется без дублирования вершин. Поэтому сумма длин всех списков считается как:
Когда мы работаем с ориентированным графом, то замечаем, что объем задействованной памяти будет меньше, чем при неориентированном (из-за отсутствия дублирования).
Сумма длин всех списков:
Со списком инцидентности все просто. Вместо вершин в список (массив) вы вставляете рёбра и потом делаете ссылки на те вершины, с которыми он связан.
К недостатку списка смежности (инцидентности) относится то что сложно определить наличие конкретного ребра (требуется поиск по списку). А если у вас большой список, то удачи вам и творческих успехов! Поэтому, чтобы работать максимальной отдачей в графе должно быть мало рёбер.
Взвешенность графа
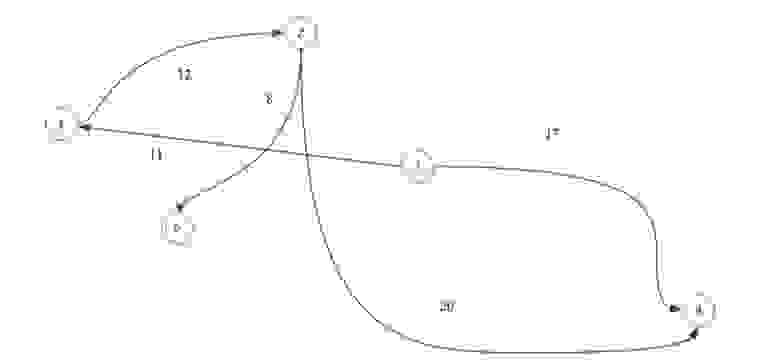
К примеру, возьмем граф с весами на ребрах:
И сделаем матрицу смежности:
В ячейках просто указываем веса ребра, а в местах где отсутствует связь пишем 0 или -∞.
Более подробно данное определение будет рассмотрено при нахождении поиска кратчайшего пути в графе.
Итак, мы завершили разбор представления графа с помощью матрицы смежности и инцидентности и списка смежности (инцидентности). Это самые известные способы представления графа. В дальнейшем мы будем рассматривать и другие матрицы, и списки, которые в свою очередь будут удобны для представления графа с определёнными особенностями.
Если заметили ошибку или есть предложения пишите в комментарии.
Алгоритмы на графах — Часть 0: Базовые понятия
Как оказалось тема алгоритмов интересна Хабра-сообществу. Поэтому я как и обещал, начну серию обзоров «классических» алгоритмов на графах.
Так как публика на Хабре разная, а тема интересна многим, я должен начать с нулевой части. В этой части я расскажу что такое граф, как он представлен в компьютере и зачем он используется. Заранее прошу прощения у тех кто это все уже прекрасно знает, но для того чтобы объяснять алгоритмы на графах, нужно сначала объяснить что такое граф. Без этого никак.
В математике, Граф — это абстрактное представление множества объектов и связей между ними. Графом называют пару (V, E) где V это множество вершин, а E множество пар, каждая из которых представляет собой связь (эти пары называют рёбрами).
Граф может быть ориентированным или неориентированным. В ориентированном графе, связи являются направленными (то есть пары в E являются упорядоченными, например пары (a, b) и (b, a) это две разные связи). В свою очередь в неориентированном графе, связи ненаправленные, и поэтому если существует связь (a, b) то значит что существует связь (b, a).
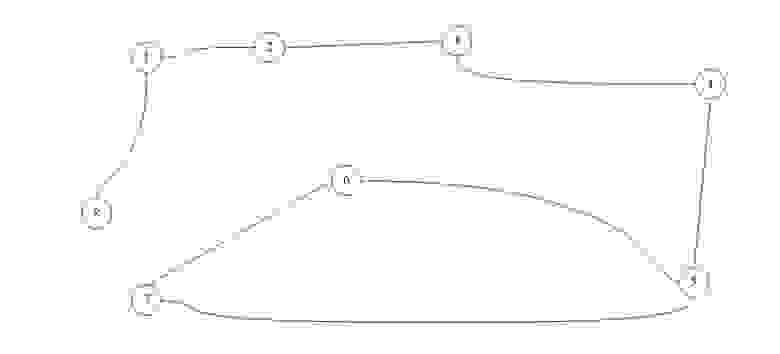
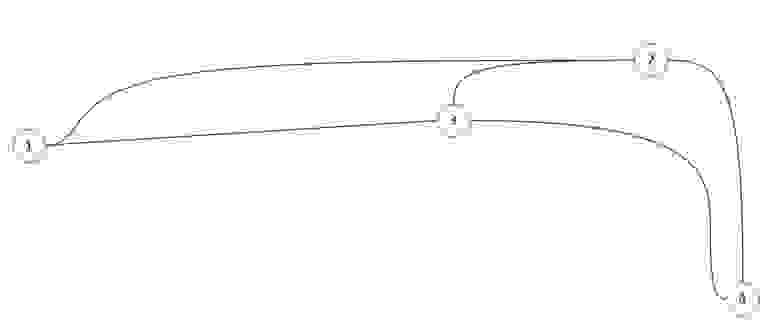
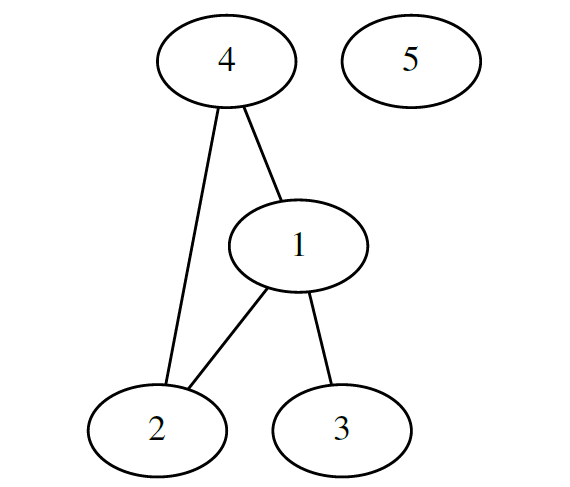
Неориентированный граф: Соседство (в жизни). Если (1) сосед (3), то (3) сосед (1). См рис. 1.а
Ориентированный граф: Ссылки. Сайт (1) может ссылаться на сайт (3), но совсем не обязательно (хотя возможно) что сайт (3) ссылается сайт (1). См рис. 1.б
Путь в графе это конечная последовательность вершин, в которой каждые две вершины идущие подряд соединены ребром. Путь может быть ориентированным или неориентированным в зависимости от графа. На рис 1.а, путем является например последовательность [(1), (4), (5)] на рис 1.б, [(1), (3), (4), (5)].
У графов есть ещё много разных свойств (например они могут быть связными, двудольными, полными), но я не буду описывать все эти свойства сейчас, а в следующих частях когда эти понятия понадобятся нам.
Представление графов
Существует два способа представления графа, в виде списков смежности и в виде матрицы смежности. Оба способа подходят для представления ориентированных и неориентированных графов.
Матрица смежности
Этот способ является удобным для представления плотных графов, в которых количество рёбер (|E|) примерно равно количеству вершин в квадрате (|V| 2 ).
В данном представлении мы заполняем матрицу размером |V| x |V| следущим образом:
A[i][j] = 1 (Если существует ребро из i в j)
A[i][j] = 0 (Иначе)
Данный способ подходит для ориентированных и неориентированных графов. Для неориентированных графов матрица A является симметричной (то есть A[i][j] == A[j][i], т.к. если существует ребро между i и j, то оно является и ребром из i в j, и ребром из j в i). Благодаря этому свойству можно сократить почти в два раза использование памяти, храня элементы только в верхней части матрицы, над главной диагональю)
Понятно что с помощью данного способа представления, можно быстро проверить есть ли ребро между вершинами v и u, просто посмотрев в ячейку A[v][u].
С другой стороны этот способ очень громоздкий, так как требует O (|V| 2 ) памяти для хранения матрицы.

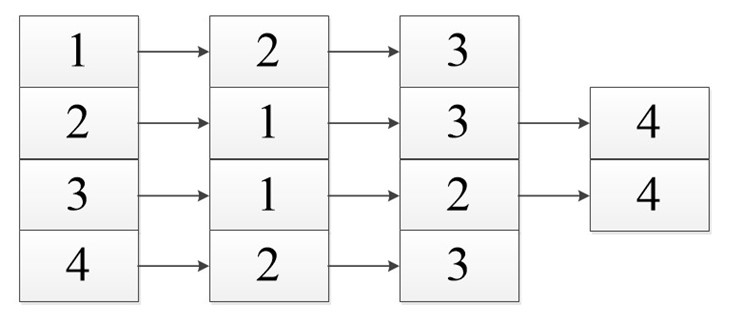
На рис. 2 приведены представления графов из рис. 1 с помощью матриц смежности.
Списки смежности
Данный способ представления больше подходит для разреженных графов, то есть графов у которых количество рёбер гораздо меньше чем количество вершин в квадрате (|E| 2 ).
В данном представлении используется массив Adj содержащий |V| списков. В каждом списке Adj[v] содержатся все вершины u, так что между v и u есть ребро. Память требуемая для представления равна O (|E| + |V|) что является лучшим показателем чем матрица смежности для разреженных графов.
Главный недостаток этого способа представления в том, что нет быстрого способа проверить существует ли ребро (u, v).

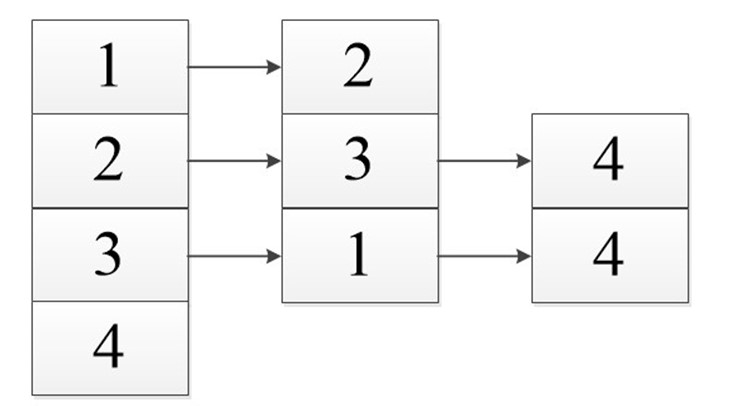
На рис. 3 приведены представления графов из рис. 1 с помощью списков смежности.
Применение
Те кто дочитал до этого места, наверное задали себе вопрос, а где же собственно я смогу применить графы. Как я и обещал я буду стараться приводить примеры. Самый первый пример который приходит в голову это социальная сеть. Вершинами графа являются люди, а ребрами отношения (дружба). Граф может быть неориентированным, то есть я могу дружить только с теми кто дружит со мной. Либо ориентированным (как например в ЖЖ), где можно добавить человека в друзья, без того чтобы он добавлял вас. Если же он да добавит вас вы будете «взаимными друзьями». То есть будет существовать два ребра: (Он, Вы) и (Вы, Он)
Ещё одно из применений графа, которое я уже упоминал это ссылки с сайта на сайт. Представим Вы хотите сделать поисковую систему и хотите учесть на какие сайты есть больше ссылок (например сайт A), при этом учитывать сколько сайтов ссылается на сайт B, который ссылается на сайт A. У вас будет матрица смежности этих ссылок. Вы захотите ввести какую то систему подсчёта рейтинга, которая делает какие то подсчёты на этой матрице, ну, а дальше… это Google (точнее PageRank) =)
Заключение
Это небольшая часть теории которая понадобится нам чтобы для следующих частей. Надеюсь вам было понятно, а главное понравилось и заинтересовало читать дальнейшие части! Оставляйте свои отзывы и пожелания в комментариях.
В следующей части
BFS — Алгоритм поиска в ширину
Библиография
Кормен, Лайзерсон, Риверст, Штайн — Алгоритмы. Построение и анализ. Издательство Вильямс, 2007.
Словарь терминов теории графов
Граф — статья в английской Википедии
Статья это кросс-пост из моего блога — «Programing as is — записки программиста»
Графы. Применение графов к решению задач
1. Методические рекомендации к теме “Графы”.
Понятие графа целесообразно вводить после того, как разобрано несколько задач, подобных задаче 1, решающее соображение в которых – графическое представление. Важно, чтобы ученики сразу осознали, что один и тот же граф может быть нарисован разными способами. Строгое определение графа, на мой взгляд, давать не нужно, т.к. оно слишком громоздко и это только затруднит обсуждение. На первых порах хватит и интуитивного понятия. При обсуждении понятия изоморфизма можно решить несколько упражнений на определение изоморфных и неизоморфных графов. Одно из центральных мест темы – теорема о четности числа нечетных вершин. Важно, чтобы ученики до конца разобрались в ее доказательстве и научились применять к решению задач. При разборе нескольких задач рекомендую не ссылаться на теорему, а фактически повторять ее доказательство. Чрезвычайно важно также понятие связности графа. Содержательным соображением здесь является рассмотрение компоненты связности, на это необходимо обратить особое внимание. Эйлеровы графы – тема почти игровая.
Первая и главная цель, которую нужно преследовать при изучении графов, –научить школьников видеть граф в условии задачи и грамотно переводить условие на язык теории графов. Не стоят рассказывать обе всем на нескольких занятиях подряд. Лучше разнести занятия по времени на 2–3 учебных года. (Прилагается разработка занятия “Понятие графа. Применение графов к решению задач” в 6 классе).
2. Теоретический материал к теме “Графы”.
Графы – замечательные математические объекты, с их помощью можно решать очень много различных, внешне не похожих друг на друга задач. В математике существует целый раздел – теория графов, который изучает графы, их свойства и применение. Мы же обсудим только самые основные понятия, свойства графов и некоторые способы решения задач.
Рассмотрим две задачи.
Решение: Нарисуем схему условия: планеты изобразим точками, а маршруты ракет – линиями.
Теперь сразу видно, что долететь с Земли до Марса нельзя.
Задача 2. Доска имеет форму двойного креста, который получается, если из квадрата 4×4 убрать угловые клетки.
Решение: Занумеруем последовательно клетки доски:
А теперь с помощью рисунка покажем, что такой обход таблицы, как указано в условии, возможен:
Мы рассмотрели две непохожие задачи. Однако решения этих двух задач объединяет общая идея – графическое представление решения. При этом и картинки, нарисованные для каждой задачи, оказались похожими: каждая картинка – это несколько точек, некоторые из которых соединены линиями.
Такие картинки и называются графами. Точки при этом называются вершинами, а линии – ребрами графа. Заметим, что не каждая картинка такого вида будет называться графом. Например. если вас попросят нарисовать в тетради пятиугольник, то такой рисунок графом не будет. Будем называть что рисунок такого вида, как в предыдущих задачах, графом, если есть какая-то конкретная задача для которой такой рисунок построен.
Другое замечание касается вида графа. Попробуйте проверить, что граф для одной и той же задачи можно нарисовать разными способами; и наоборот для разных задач можно нарисовать одинаковые по виду графы. Здесь важно лишь то, какие вершины соединены друг с другом, а какие – нет. Например, граф для задачи 1 можно нарисовать по-другому:
Такие одинаковые, но по-разному нарисованные графы, называются изоморфными.
Степени вершин и подсчет числа ребер графа
Запишем еще одно определение: Степенью вершины графа называется количество выходящих из нее ребер. В связи с этим, вершина, имеющая четную степень, называется четной вершиной, соответственно, вершина, имеющая нечетную степень, называется нечетной вершиной.
С понятием степени вершины связана одна из основных теорем теории графов –теорема о честности числа нечетных вершин. Докажем ее мы немного позднее, а сначала для иллюстрации рассмотрим задачу.
Решение: Допустим, что такое соединение телефонов возможно. Тогда представим себе граф, в котором вершины обозначают телефоны, а ребра – провода, их соединяющие. Подсчитаем, сколько всего получится проводов. К каждому телефону подключено ровно 5 проводов, т.е. степень каждой вершины нашего графа – 5. Чтобы найти число проводов, надо просуммировать степени всех вершин графа и полученный результат разделить на 2 (т.к. каждый провод имеет два конца, то при суммировании степеней каждый провод будет взят 2 раза). Но тогда количество проводов получится разным 
Ответ. Соединить телефоны таким образом невозможно.
Теорема: Любой граф содержит четное число нечетных вершин.
Доказательство: Количество ребер графа равно половине суммы степеней его вершин. Так как количество ребер должно быть целым числом, то сумма степеней вершин должна быть четной. А это возможно только в том случае, если граф содержит четное число нечетных вершин.
Есть еще одно важное понятие, относящееся к графам – понятие связности.
Граф называется связным, если из любые две его вершины можно соединить путем, т.е. непрерывной последовательностью ребер. Существует целый ряд задач, решение которых основано на понятии связности графа.
Задача 4. В стране Семерка 15 городов, каждый из городов соединен дорогами не менее, чем с семью другими. Докажите, что из каждого города модно добраться в любой другой.
Доказательство: Рассмотрим два произвольных А и В города и допустим, что между ними нет пути. Каждый из них соединен дорогами не менее, чем с семью другими, причем нет такого города, который был бы соединен с обоими рассматриваемыми городами (в противном случае существовал бы путь из A в B). Нарисуем часть графа, соответствующую этим городам:
Теперь явно видно, что мы получили не менее различных 16 городов, что противоречит условию задачи. Значит утверждение доказано от противного.
Если принять во внимание предыдущее определение, то утверждение задачи можно переформулировать и по-другому: “Доказать, что граф дорог страны Семерка связен.”
Теперь вы знаете, как выглядит связный граф. Несвязный граф имеет вид нескольких “кусков”, каждый из которых – либо отдельная вершина без ребер, либо связный граф. Пример несвязного графа вы видите на рисунке:
Каждый такой отдельный кусок называется компонентой связности графа. Каждая компонента связности представляет собой связный граф и для нее выполняются все утверждения, которые мы доказали для связных графов. Рассмотрим пример задачи, в которой используется компонента связности:
Задача 5. В Тридевятом царстве только один вид транспорта – ковер-самолет. Из столицы выходит 21 ковролиния, из города Дальний – одна, а из всех остальных городов, – по 20. Докажите, что из столицы можно долететь в город Дальний.
Доказательство: Понятно, что если нарисовать граф ковролиний Царства, то он может быть несвязным. Рассмотрим компоненту связности, которая включает в себя столицу Царства. Из столицы выходит 21 ковролиния, а из любых других городов, кроме города Дальний – по 20, поэтому, чтобы выполнялся закон о четном числе нечетных вершин необходимо, чтобы и город Дальний входил в эту же самую компоненту связности. А так как компонента связности – связный граф, то из столицы существует путь по ковролиниям до города Дальний, что и требовалось доказать.
Вы наверняка сталкивались с задачами, в которых требуется нарисовать какую-либо фигуру не отрывая карандаш от бумаги и проводя каждую линию только один раз. Оказывается, что такая задача не всегда разрешима, т.е. существуют фигуры, которые указанным способом нарисовать нельзя. Вопрос разрешимости таких задач также входит в теорию графов. Впервые его исследовал в 1736 году великий немецкий математик Леонард Эйлер, решая задачу о Кенигсбергских мостах. Поэтому графы, которые можно нарисовать указанным способом, называются Эйлеровыми графами.
Решение. Если мы будем рисовать граф так, как сказано в условии, то в каждую вершину, кроме начальной и конечной, мы войдем столько же раз, сколько выйдем из нее. То есть все вершины графа, кроме двух должны быть четными. В нашем же графе имеется три нечетные вершины, поэтому его нельзя нарисовать указанным в условии способом.
Сейчас мы доказали теорему об Эйлеровых графах:
Теорема: Эйлеров граф должен иметь не более двух нечетных вершин.
И в заключение – задача о Кенигсбергских мостах.
Задача 7. На рисунке изображена схема мостов города Кенигсберга.
Можно ли совершить прогулку так, чтобы пройти по каждому мосту ровно 1 раз?
3. Задачи к теме “Графы”
Понятие графа.
1. На квадратной доске 3×3 расставлены 4 коня так, как показано на рис.1. Можно ли сделав несколько ходов конями, переставить их в положение, показанное на рис.2?
 |
Рис. 1

Решение. Занумеруем клетки доски, как показано на рисунке:
Каждой клетке поставим в соответствие точку на плоскости и, если из одной клетки можно попасть в другую ходом шахматного коня, то соответствующие точки соединим линией. Исходная и требуемая расстановки коней показаны на рисунках:
 |  |
При любой последовательности ходов конями порядок их следования, очевидно, измениться не может. Поэтому переставить коней требуемым образом невозможно.
Решение. Поставив в соответствие каждому городу точку и соединив точки линией, если сумма цифр делится на 3, получим граф, в котором цифры 3, 5, 9 связаны между собой, но не связаны с остальными. Значит долететь из города 1 в город 9 нельзя.
Степени вершин и подсчет числа ребер.
3. В государстве 100 городов к из каждого города выходит 4 дороги. Сколько всего дорог в государстве.
Решение. Подсчитаем общее количество выходящих городов дорог – 100 . 4 = 400. Однако при таком подсчете каждая дорога посчитана 2 раза – она выходит из одного города и входит в другой. Значит всего дорог в два раза меньше, т.е. 200.
Ответ. Нет (теорема о четности числа нечетных вершин).
Ответ. Нет, не может.
6. Может ли в государстве, в котором из каждого города выходит ровно 3 дороги, быть ровно 100 дорог?
Решение. Подсчитаем число городов. Число дорог равно числу городов х, умноженному на 3 (число выходящих из каждого города дорог) и разделенному на 2 (см. задачу 3). Тогда 100 = Зх/2 => Зх=200, чего не может быть при натуральном х. Значит 100 дорог в таком государстве быть не может.
7. Докажите, что число людей, живших когда-либо на Земле и сделавших нечетное число рукопожатий, четно.
Доказательство непосредственно следует из теоремы о четности числа нечетных вершин графа.
Связность.
8. В стране из каждого города выходит 100 дорог и из каждого города можно добраться до любого другого. Одну дорогу закрыли на ремонт. Докажите, что и теперь из любого города можно добраться до любого другого.
Доказательство. Рассмотрим компоненту связности, в которую входит один из городов, дорогу между которыми закрыли. По теореме о четности числа нечетных вершин в нее входит и второй город. А значит по-прежнему можно найти маршрут и добраться из одного из этих городов в другой.
Графы Эйлера.
9. Имеется группа островов, соединенных мостами так, что от каждого острова можно добраться до любого другого. Турист обошел все острова, пройдя по каждому мосту розно 1 раз. На острове Троекратном он побывал трижды. Сколько мостов ведет с Троекратного, если турист
а) не с него начал и не на нем закончил?
б) с него начал, но не на нем закончил?
в) с него начал и на нем закончил?
10. На рисунке изображен парк, разделенный на несколько частей заборами. Можно ли прогуляться по парку и его окрестностям так, чтобы перелезть через каждый забор розно 1 раз?