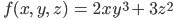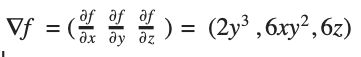что такое градиентный спуск

Метод градиентного спуска

Материал из MachineLearning.

Содержание

Введение

Пусть функция такова, что можно вычислить ее градиент. Тогда можно применить метод градиентного спуска, описанный в данной статье.

В статье приведены теоремы сходимости метода градиентного спуска, а также рассмотрена его варианты:

Метод градиентного спуска

Идея метода

Основная идея метода заключается в том, чтобы осуществлять оптимизацию в направлении наискорейшего спуска, а это направление задаётся антиградиентом :

Алгоритм

Выход: найденная точка оптимума

Критерий останова

Критерии остановки процесса приближенного нахождения минимума могут быть основаны на различных соображениях. Некоторые из них:

Сходимость градиентного спуска с постоянным шагом

Теорема 1 о сходимости метода градиентного спуска спуска с постоянным шагом.

Тогда при любом выборе начального приближения.

В условиях теоремы градиентный метод обеспечивает сходимость либо к точной нижней грани (если функция не имеет минимума) либо к значению Существуют примеры, когда в точке реализуется седло, а не минимум. Тем не менее, на практике методы градиентного спуска обычно обходят седловые точки и находят локальные минимумы целевой функции.

Определение. Дифференцируемая функция называется сильно выпуклой (с константой 0″ alt= «\Lambda>0» />), если для любых и из справедливо

Теорема 2 о сходимости метода градиентного спуска спуска с постоянным шагом.

Тогда при любом выборе начального приближения.

Выбор оптимального шага

При таком выборе шага оценка сходимости будет наилучшей и будет характеризоваться величиной:

Но даже для хорошо обусловленных функций проблема выбора шага нетривиальна в силу отсутствия априорной информации о минимизируемой функции. Если шаг выбирается малым (чтобы гарантировать сходимость), то метод сходится медленно. Увеличение же шага (с целью ускорения сходимости) может привести к расходимости метода. Далее будут описаны два алгоритма автоматического выбора шага, позволяющие частично обойти указанные трудности.

Градиентный метод с дроблением шага

В этом варианте градиентного метода величина шага на каждой итерации выбирается из условия выполнения неравенства

где — некоторая заранее выбранная константа.

Метод наискорейшего спуска

Этот вариант градиентного метода основывается на выборе шага из следующего соображения. Из точки будем двигаться в направлении антиградиента до тех пор пока не достигнем минимума функции f на этом направлении, т. е. на луче :

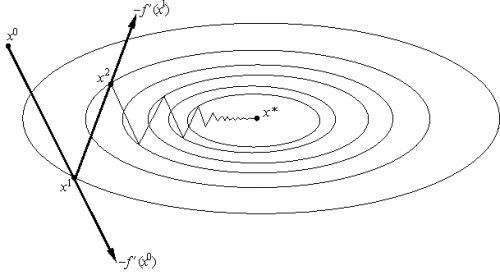
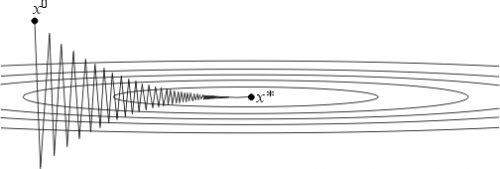
Другими словами, выбирается так, чтобы следующая итерация была точкой минимума функции f на луче L (см. рис. 3). Такой вариант градиентного метода называется методом наискорейшего спуска. Заметим, кстати, что в этом методе направления соседних шагов ортогональны.

Метод наискорейшего спуска требует решения на каждом шаге задачи одномерной оптимизации. Практика показывает, что этот метод часто требует меньшего числа операций, чем градиентный метод с постоянным шагом.

В общей ситуации, тем не менее, теоретическая скорость сходимости метода наискорейшего спуска не выше скорости сходимости градиентного метода с постоянным (оптимальным) шагом.

Числовые примеры

Метод градиентного спуска с постоянным шагом

Для исследования сходимости метода градиентного спуска с постоянным шагом была выбрана функция:

Результаты эксперимента отражены в таблице:

Из полученных результатов можно сделать вывод, что при слишком большом чаге метод расходится, при слишком малом сходится медленно и точчность хуже. Надо выбирать шаг наибольшим из тех, при которых метод сходится.

Градиентный метод с дроблением шага

Для исследования сходимости метода градиентного спуска с дроблением шага (2) была выбрана функция:

Результаты эксперимента отражены в таблице:

Метод наискорейшего спуска

Для исследования сходимости метода наискорейшего спуска была выбрана функция:

Для решения одномерных задач оптимизации использован метод золотого сечения.

Метод получил точность 6e-8 за 9 итераций.

Отсюда можно сделать вывод, что метод наискорейшего спуска сходится быстрее, чем градиентный метод с дроблением шага и метод градиентного спуска с постоянным шагом.

Недостатком методом наискорейшего спуска явлляется необходимость решать одномерную задачу оптимизации.

Рекомендации программисту

При программировании методов градиентного спуска следует аккуратно относится к выбору параметров, а именно

Заключение

Методы градиентного спуска являются достаточно мощным инструментом решения задач оптимизации. Главным недостатком методов является ограниченная область применимости.

Источник

Введение в градиентный спуск

Дата публикации May 13, 2019

Этот блог будет охватывать следующие вопросы и темы:

1. Что такое градиент?

2. Что такое градиентный спуск?

3. Три общих градиентных спуска

4. Реализация в Python

1. Градиент

Рисунок функции показан ниже, и мы видим, что минимум функции равен (0, 0).

В этом случае x-компонент градиента является частной производной по x, а y-компонент градиента является частной производной по y. Градиент функции выше:

Если мы хотим найти направление, которое увеличивает функцию максимум в точке (1, 2), мы можем подключить (1, 2) к формуле выше и получить:

2. Градиентный спуск

Учитывая отправную точку:

Мы можем построить итерационную процедуру:

Параметр альфа в приведенной выше формуле называется скоростью обучения, которая в большинстве случаев является небольшой константой и находится в диапазоне от 0 до 1. Итерационная процедура не остановится, пока не сойдется. Взяв предыдущий пример, мы уже знали, что градиент:

Поэтому итерационная процедура градиентного спуска может быть записана как:

Тогда мы можем получить:

Наконец, предполагая, что альфа меньше 1, тогда мы можем получить:

Вывод такой же, как мы видим на рисунке выше.

В машинном обучении мы уделяем больше внимания взаимосвязи между функцией стоимости и параметрами, а не зависимыми и независимыми переменными. Общая идея градиентного спуска в машинном обучении заключается в итерационной настройке параметров для минимизации функции стоимости.

В некоторых случаях мы можем применить уравнение в замкнутой форме для непосредственного расчета параметров, которые наилучшим образом соответствуют модели для набора данных обучения. Например, чтобы минимизировать MSE для линейной регрессии, параметры могут быть записаны как:

Однако в других случаях у нас нет уравнения в замкнутой форме, такого как логистическая регрессия. Поэтому применяется итеративный подход к оптимизации, такой как градиентный спуск.

Важным параметром в градиентном спуске является скорость обучения, которая определяет размер каждого шага. Когда скорость обучения слишком велика, градиентный спуск может перепрыгнуть через долину и оказаться на другой стороне. Это приведет к расхождению функции стоимости. С другой стороны, когда скорость обучения слишком мала, алгоритм будет сходиться долго. Следовательно, перед началом градиентного спуска необходима правильная скорость обучения.

3. Три типичных градиентных спуска

Мы рассмотрим несколько вариантов градиентного спуска, которые широко используются в машинном обучении: пакетный градиентный спуск, мини-пакетный градиентный спуск и стохастический градиентный спуск.

Пакетный градиентный спуск

Пакетный градиентный спуск использует всю партию обучающих данных на каждом шаге. Он рассчитывает ошибку для каждой записи и принимает среднее значение для определения градиента Преимущество Batch Gradient Descent заключается в том, что алгоритм более эффективен в вычислительном отношении и обеспечивает стабильный путь обучения, что облегчает сходимость. Тем не менее, пакетный градиентный спуск занимает больше времени, когда тренировочный набор большой.

Стохастический градиентный спуск

В другом крайнем случае Stochastic Gradient Descent просто выбирает один экземпляр из обучающего набора на каждом шаге и обновляет градиент только на основе этой отдельной записи. Преимущество Stochastic Gradient Descent заключается в том, что алгоритм намного быстрее на каждой итерации, что устраняет ограничение в Batch Gradient Descent. Однако алгоритм дает менее регулярный и стабильный путь обучения по сравнению с пакетным градиентным спуском. Вместо плавного уменьшения функция стоимости будет подпрыгивать вверх и вниз. После раундов итераций алгоритм может найти хороший параметр, но конечный результат не обязательно является глобальным оптимальным.

Мини-пакетный градиентный спуск

Мини-пакетный градиентный спуск сочетает в себе концепцию пакетного и стохастического градиентного спуска. На каждом этапе алгоритм вычисляет градиент на основе подмножества обучающего набора вместо полного набора данных или только одной записи. Преимущество мини-пакетного градиентного спуска в том, что алгоритм может использовать преимущества матричной операции во время расчета, а функция стоимости может уменьшаться более плавно и стабильно, чем стохастический градиентный спуск.

4. Реализация в Python

В этой части я буду использовать известную радужную оболочку набора данных, чтобы показать, как работает градиент, достойный при логистической регрессии.

Сначала импортируйте пакет.

Далее загрузите данные. Обратите внимание, что для простоты я выбираю только 2 вида ириса.

Пакетный градиентный спуск

Стохастический градиентный спуск

Мини-пакет Gradient Descent

Из рисунка выше мы можем видеть, что три вида градиентных спусков генерируют одинаковую границу линейного решения.

Резюме

В этом посте вы узнали много нового о градиентном спуске. Теперь вы знаете основную математику, лежащую в основе градиента, и понимаете, как работает алгоритм за сценой. Во-вторых, вы узнали, почему скорость обучения и нормализация так важны для успеха алгоритма. Наконец, вы узнали о наиболее распространенных типах градиентного спуска и о том, как реализовать эти алгоритмы в python. Эти знания позволяют вам лучше понять машинное обучение и глубокое обучение. Вы можете прочитать больше блогов, нажав на следующую ссылку:

Тур по машинному обучению и глубокому обучению

Эта серия блогов будет иметь представление о глубоком изучении с точки зрения теории и реализации.

medium.com

[1] Орелиен Жерон, практическое машинное обучение с Scikit-Learn & TensorFlow, 2018

[2] Ян Гудфеллоу, Йошуа Бенжио, Аарон Курвилль, (2017)Глубокое обучение

Источник

Математика для искусственных нейронных сетей для новичков, часть 2 — градиентный спуск

В первой части я забыл упомянуть, что если случайно сгенерированные данные не по душе, то можно взять любой подходящий пример отсюда. Можно почувствовать себя ботаником, виноделом, продавцом. И все это не вставая со стула. В наличии множество наборов данных и одно условие — при публикации указывать откуда взял данные, чтобы другие смогли воспроизвести результаты.

Градиентный спуск

В прошлой части был показан пример вычисления параметров линейной регрессии с помощью метода наименьших квадратов. Параметры были найдены аналитически — , где — псевдообратная матрица. Это решение наглядное, точное и короткое. Но есть проблема, которую можно решить численно. Градиентный спуск — метод численной оптимизации, который может быть использован во многих алгоритмах, где требуется найти экстремум функции — нейронные сети, SVM, k-средних, регрессии. Однако проще его воспринять в чистом виде (и проще модифицировать).

Проблема заключается в том, что вычисление псевдообратной матрицы очень затратно: 2 умножения по , нахождение обратной матрицы — , умножение матрицы вектор , где n — количество элементов в матрице A (количество признаков * количество элементов в тестовой выборке) Если количество элементов в матрице A велико (> 10^6 — например), то даже если в наличии 10000 ядер, нахождение решения аналитически может затянуться. Также первая производная может оказаться нелинейной, что усложнит решение, аналитического решения может не оказаться вовсе или данные могут просто не влезть в память и потребуется итеративный алгоритм. Бывает, что в плюсы записывают и то, что численное решение не идеально точное. В связи с этим функцию стоимости минимизируют численными методами. Задачу нахождения экстремума называют задачей оптимизации. В этой части я остановлюсь на методе оптимизации, который называется градиентный спуск.

Не будем отходить от линейной регрессии и МНК и обозначим функцию потерь как — она осталась неизменной. Напомню, что градиент — это вектор вида , где — это частная производная. Одним из свойств градиента является то, что он указывает направление, в котором некоторая функция f возрастает больше всего. Доказательство этого следует из определения производной. Пара доказательств. Возьмем некоторую точку a — в окрестности этой точки функция F должна быть определена и дифференцируема, тогда вектор антиградиента будет указывать на направление, в котором функция F убывает быстрее всего. Отсюда делается вывод, что в некоторой точке b, равной , при некотором малом значение функции будет меньше либо равным значению в точке а. Можно представить это, как движение вниз по холму — сделав шаг вниз, текущая позиция будет ниже, чем предыдущая. Таким образом, на каждом следующем шаге высота будет как минимум не увеличиваться. Формальное определение. Исходя из этих определений можно получить формулу для нахождения неизвестных параметров (это просто переписанная версия формулы выше):

— это шаг метода. В задачах машинного обучения его называют скоростью обучения.

Метод очень прост и интуитивен, возьмем простой двумерный пример для демонстрации:

Необходимо минимизировать функцию вида . Минимизировать значит найти при каком значении функция принимает минимальное значение. Определим последовательность действий:

1) Необходима производная по :
2) Установим начальное значение = 0
3) Установим размер шага — попробуем несколько значений — 0.1, 0.9, 1.2, чтобы посмотреть как этот выбор повлияет на сходимость.
4) 25 раз подряд выполним указанную выше формулу: Так как неизвестный параметр только один, то и формула только одна.

Код крайне прост. Исключая определение функций, весь алгоритм уместился в 3 строки:

Весь процесс можно визуализировать примерно так (синяя точка — значение на предыдущем шаге, красная — текущее):

Или же для шага другого размера:

При значении, равном 1.2, метод расходится, каждый шаг опускаясь не ниже, а наоборот выше, устремляясь в бесконечность. Шаг в простой реализации подбирается вручную и его размер зависит от данных — на каких-нибудь ненормализованных значениях с большим градиентом и 0.0001 может приводить к расхождению.

Вот еще пример с «плохой» функцией. В первой анимации метод также расходится и будет долго блуждать по холмам из-за слишком высокого шага. Во втором случае был найден локальный минимум и варьируя значение скорости не получится заставить метод найти минимум глобальный. Этот факт является одним недостатков метода — он может найти глобальный минимум только если функция выпуклая и гладкая. Или если повезет с начальными значениями.

Плохая функция:

Также возможно рассмотреть работу алгоритма на трехмерном графике. Часто рисуют только изолинии какой-то фигуры. Я взял простой параболоид вращения: . В 3D выглядит он так: , а график с изолиниями — «вид сверху».

Также обратите внимание, что все линии градиента, направлены перпендикулярно изолиниям. Это означает, что двигаясь в сторону антиградиента, не получится за один шаг сразу же прыгнуть в минимум — градиент указывает совсем не туда.

После графического пояснения, найдем формулу для вычисления неизвестных параметров линейной регрессии с МНК.

Если бы количество элементов в тестовой выборке было равно единице, то формулу можно было бы так и оставить и считать. В случае, когда в наличии n элементов алгоритм выглядит так:

Повторять v раз
<

для каждого j одновременно.
>, где n — количество элементов в обучающей выборке, v — количество итераций

Требование одновременности означает, что производная должна быть вычислена со старыми значениями theta, не стоит вычислять сначала отдельно первый параметр, затем второй и т.д., потому что после изменения первого параметра отдельно, производная также изменит свое значение. Псевдокод одновременного изменения:

Если вычислять значения параметров по одиночке, то это уже будет не градиентный спуск. Допустим, у нас трехмерная фигура и если вычислять параметры один за одним, то можно представить этот процесс как движение только по одной координате за раз — один шажок по x координате, затем шажок по y координате и т.д. ступеньками, вместо движения в сторону вектора антиградиента.

Приведенный выше вариант алгоритма называют пакетный градиентный спуск. Количество повторений можно заменить на фразу «Повторять, пока не сойдется». Эта фраза означает, что параметры будут корректироваться до тех пор, пока предыдущее и текущее значения функции стоимости не сравняются. Это значит, что локальный или глобальный минимум найден и дальше алгоритм не пойдет. На практике равенства достичь невозможно и вводится предел сходимости . Его устанавливают какой-нибудь малой величиной и критерием остановки является то, что разность предыдущего и текущего значений меньше предела сходимости — это значит, что минимум достигнут с нужной, установленной точностью. Выше точности (меньше ) — больше итераций алгоритма. Выглядит это как-то так:

Так как пост неожиданно растянулся, я бы хотел его на этом завершить — в следующей части я продолжу разбор градиентного спуска для линейной регрессии с МНК.

Источник

Разбираем нейросети по частям: как работает градиентный спуск

Градиентный спуск — это способ поиска точек минимума или максимума в сложных функциях. Рассказываем, почему это так важно для обучения нейросетей

Нейросети сейчас везде, и даже цифровому гуманитарию от них не скрыться. Word2vec при помощи нейросети кодирует смысл слов (вот тут мы объясняли, как), а новые модели ELMO и BERT даже научились учитывать, что слова появляются в разных контекстах и от этого из смысл тоже может меняться. Этот текст — про то, что значит «обучить» нейросеть и кто «подбирает веса» отдельных нейронов.

А что вообще творится в нейросетях? Напомните!

Ранее мы рассказывали, как «сырые» данные (картинка, видео или текст) разбиваются на мелкие кусочки и подаются на каждый входной нейрон. Дальше входные нейроны анализируют что-то очень простое — есть ли в их кусочке картинки 10 белых пикселей, есть ли буква «Т» в слове — и если да, нейрон «активируется», то есть передает свой сигнал в следующий слой с определенной силой. Сигналы комбинируются, потом собираются в абстрактные комбинации десятков комбинаций сигналов, и в конце концов активируют один из нейронов, который классифицирует картинку как котика или хлеб.

А как активируется нейрон?

Нейрон — это функция, которая получает на вход числа (обычно много), что-то с ними делает и возвращает одно число (обычно от 0 до 1). Функция, из которой нейрон состоит, называется функцией активации, или передаточной функцией. Именно она отвечает за то, будет ли передан сигнал нейрона дальше (1 на выходе функции — если будет, 0 — если нет). В самом простом виде функция активации может быть пороговой:

В данном случае, если какие-то значения на входе нейрона дали положительную сумму — нейрон активировался. Порог активации здесь выглядит как вертикальная палочка, простой переключатель вкл/выкл, а значит, нейрон может быть либо активен, либо нет — как лампочка. Есть и более сложные функции, которые могут изменять силу выходного сигнала, могут «чуть-чуть активировать» нейрон, или «активировать его посильнее»:

Выбор функции активации нейронов влияет на то, какие задачи они могут решать, и их подбор — задача создателя нейросети. Если создатель понимает, какие функции для чего подходят, у него больше шансов сделать крутую нейросеть, которая решит его проблему.

Вот главное: нейрон — это функция. Чем больше ее значение, тем важнее сигнал нейрона для всей сети.

Почему это важно в контексте обучения нейросети?

Коротко: нейроны постоянно дают слишком сильный или слабый сигнал и сбивают предсказание, их нужно настраивать.

Нейроны глупые! Без ручной настройки силы их выходных сигналов нейросеть даёт случайные предсказания. К выходному значению нейрона можно (и нужно) прибавлять некоторый вес. Вес прибавляется или отнимается в зависимости от того, насколько сильно в прошлый раз нейросеть ошиблась с предсказанием. Этот этап работы, когда нейроны штрафуются за все прошлые «косяки», называется обратным распространением ошибки. Какие-то нейроны активируются слишком сильно, какие-то — слабо, но все равно они уводят предсказание нейросети в сторону от правильного. Поскольку нейронов слишком много, и за какие конкретно признаки каждый из них отвечает — неясно, настроить каждый вес вручную невозможно. Люди придумали способ настраивать веса автоматически.

Для этого существует функция потерь. Что она делает?

Коротко: ее значение возрастает, если нейросеть сильно ошибается. Значит, надо найти такое решение, где функция возрастать не будет.

Есть функция, возрастающая при сильной ошибке предсказания. Чем больше ошибка, тем сильнее уменьшаются (штрафуются) веса активированных нейронов. Человеку нужно свести меру ошибки к минимуму, научить нейросеть делать верные предсказания о том, котик на картинке или булочка. Если функция потерь дает высокие значения при большой ошибке, мы просто ищем такие веса, при которых она дает минимальные значения.

Кстати, функций потерь тоже существует много, они по-разному подходят для разных задач, и крутые программисты за 300к/сек знают, как в них сориентироваться. Функции потерь объединяет то, что они возрастают вместе с мерой ошибки предсказания. Она вычисляется просто: из числа X (предсказанного) вычитаем число Y (то, что должно было предсказаться) — получаем число Err. Оно становится одним из аргументов функции потерь.

Здесь надо вспомнить производные

Задача подбора весов нейронной сети также называется тренировкой или задачей оптимизации. (Ведь optimus — наилучший, а значит, мы и ищем лучшие веса?) Веса нам нужны те, при которых функция потерь принимает минимальное значение. Когда мы знаем это значение, рассчитать нужные веса становится легко — все равно, что решить уравнение.

А значит, желаемая схема обучения нейросети выглядит примерно так:
Функция потерь принимает минимальное значение → находим соответствующие этому значению веса → ошибка минимальна → предсказание нейросети точно → вы великолепны.

Только сначала нужно найти минимальное значение функции.

Как это делали в школе?

Когда на уроке алгебры учительница давала какой-нибудь многочлен и просила найти его минимум, мы поступали следующим образом:

Напомним, что производная функции выражает скорость ее возрастания или убывания. Её геометрический смысл — показать угол, под которым в данной точке проходит касательная к функции. Если производную (а значит, угол касательной) приравнять к нулю, то мы найдем точки, в которых касательная параллельна оси абсцисс.

Вот что это будут за точки: в них функция меняет направление. Такие точки обязательно становятся (хотя бы локальными) минимумами или максимумами функции. А вот как будут выглядеть касательные к этим точкам:

После этого (страшного или приятного?) математического флешбэка пора признаваться, что как раз вот так в нейронных сетях найти минимум функции потерь невозможно. У нее слишком много входных аргументов, и аналитические подходы (как показанный выше) не работают. Приходится применять специальный поисковой, пошаговый метод градиентного спуска (умное слово для него — «эвристический», то есть все тот же «поисковой», но еще умнее — по-гречески).

Вот главное: нам до сих пор нужно найти минимальное значение функции потерь, это минимизирует ошибку в предсказании нейросети. Но мы сейчас выяснили, что по-школьному это сделать не получится.

We need to go deeper

Если есть функция, зависящая от нескольких переменных, можно говорить о частной производной, то есть о такой производной, когда все остальные переменные, кроме той, которая нам интересна, становятся константами (то есть постоянными).

Поэтому вот вам таблица, попробуйте сказать, чему равна частная производная от переменной x функции

Помните, что если рассчитывать производную от x, то z становится константой и с ней ничего делать не нужно.

(Ответ будет чуть ниже, не подглядывайте!)

Математически фразу «производная функции y от переменной x» можно записать так:

Ответ к задаче: частная производная равна

Чему же равна частная производная в точке (x=3, z=4)? Теперь мы можем просто подставить значения 3 и 4 в полученное уравнение частной производной

Мы получим, что производная равна 23 + 44 = 22.

Пора рассказать, что такое градиент

Если для функции многих переменных по очереди рассчитать частные производные для каждой из переменных (и записать эти производные в ряд, и взять в скобочки), получится вектор, называемый градиентом. Так как одна переменная соответствует одной координатной оси, каждый элемент вектора показывает скорость изменения функции вдоль своей оси, а все вместе они показывают направление, в котором быстрее всего возрастает функция в целом.

Вот главное: градиент — это вектор, показывающий направление, в котором функция многих переменных быстрее всего возрастает или падает. «Градиент функции f» записывается так: ∇f (можно читать как «набла f»).

Вот небольшое упражнение. Попробуйте найти градиент функции

для переменных x, y, z?
Подсказка: должен получиться вектор с тремя элементами.

Сложность в том, чтобы уследить, какие из «констант» — множители переменной, что рассматриваются в данный момент, а какие — отбрасываются как слагаемые.

Объясните наконец, что такое градиентный спуск!

Градиентный спуск — это эвристический алгоритм, который выбирает случайную точку, рассчитывает направление скорейшего убывания функции (пользуясь градиентом функции в данной точке), а затем пошагово рассчитывает новые значения функции, двигаясь в выбранную сторону. Если убывание значения функции становится слишком медленным, алгоритм останавливается и говорит, что нашел минимум.

Стоит помнить, что говорим не о двумерных функциях. Представить, что происходит, можно по этой картинке:

Градиентный спуск выбирает случайную точку, находит направление самого быстрого убывания функции и двигается до ближайшего минимума вдоль этого направления. Кстати, размер одного шага можно настроить, это бывает очень важно. Если на каком-то этапе разность между старой точкой (до шага) и новой снижается ниже предела, считается, что минимум найден, алгоритм завершен. Можно вообразить работу градиентного спуска как игру в «холодно-горячо» до тех пор, пока степень «потепления» не станет пренебрежительно малой.

Вот главное:

Источник