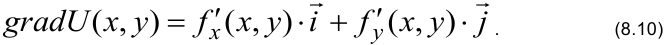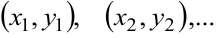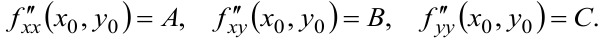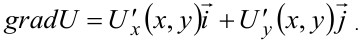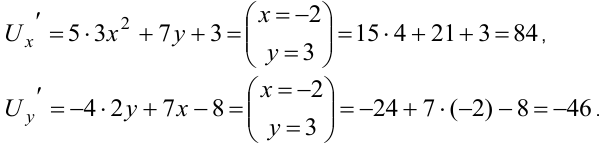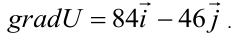что такое градиент в математике простыми словами
Значение слова «градиент»
[От лат. gradiens, gradientis — шагающий]
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
, значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный скорости роста этой величины в этом направлении.
Например, если взять в качестве
высоту поверхности земли над уровнем моря, то её градиент в каждой точке поверхности будет показывать «направление самого крутого подъёма», и своей величиной характеризовать крутизну склона.
С математической точки зрения на градиент можно смотреть как на:
1. Коэффициент линейности изменения значения функции многих переменных от изменения значения аргумента
2. Вектор в пространстве области определения скалярной функции многих переменных, составленный из частных производных
3. Строки Матрицы Якоби содержат градиенты составных скалярных функций из которых состоит векторная функция многих переменных
Пространство, на котором определена функция и её градиент, может быть, вообще говоря, как обычным трёхмерным пространством, так и пространством любой другой размерности любой физической природы или чисто абстрактным (безразмерным).
Термин впервые появился в метеорологии, а в математику был введён Максвеллом в 1873 г. Обозначение grad тоже предложил Максвелл.
Градиент
Градиент [gradient] — вектор, направленный в сторону наискорейшего возрастания функции и равный по величине ее производной в этом направлении:
где символами ei обозначены единичные векторы осей координат (орты).
Смотреть что такое «Градиент» в других словарях:
ГРАДИЕНТ — (лат.). Разность в барометрических и термометрических показаниях в разных местностях. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ГРАДИЕНТ разность в показаниях барометра и термометра в один и тот же момент… … Словарь иностранных слов русского языка
ГРАДИЕНТ — [от лат. gradiens (gradientis) шагающий], мера изменения какой либо физической величины в пространстве на единицу длины (расстояния) в том направлении, в котором она убывает наиболее быстро. Понятием градиента широко пользуются в метеорологии,… … Экологический словарь
ГРАДИЕНТ — векторная величина, характеризующая скорость изменения физ. поля по направлению (напр., температурный градиент, вертикальный градиент силы тяжести и т. п.). Г. можно получить расчетным путем (в простейшем случае как разность значений поля в двух… … Геологическая энциклопедия
градиент — Изменение значения некоторой величины на единицу расстояния в заданном направлении. Топографический градиент — это изменение высоты местности на измеренном по горизонтали расстоянии. [http://www.oceanographers.ru/index.php?option=com… … Справочник технического переводчика
градиент — 1. Изменение значения любой переменной величины, чаще всего используется в метеорологии, например, градиент температуры, барометрический градиент. 2. Крутизна склона, выраженная в градусах, процентах или как отношение … Словарь по географии
градиент — вектор Словарь русских синонимов. градиент сущ., кол во синонимов: 2 • вектор (5) • … Словарь синонимов
градиент — а, м. gradient m., лат. gradiens. Мера возрастания или убывания в пространстве какой л. физической величины при перемещении на единицу длины. БАС 2. Лекс. Брокг.: градиент; Уш. 1935: градие/нт; БСЭ 2: градие/нтный ветер; БСЭ 3: градиентоме/тр,… … Исторический словарь галлицизмов русского языка
ГРАДИЕНТ — ГРАДИЕНТ, в метеорологии и геофизике быстрота изменения некоторого элемента (температуры, давления, электрич. поля) в направлении, перпендикулярном к поверхностям уровня (т. е. поверхностям равных температур, равных давлений и пр.). Градиент… … Большая медицинская энциклопедия
градиент — закономерное количественное изменение, отражающее убывание или возрастание некоего свойства или показателя, например, градиент раздражителя (см. таксис). Словарь практического психолога. М.: АСТ, Харвест. С. Ю. Головин. 1998 … Большая психологическая энциклопедия
ГРАДИЕНТ — ГРАДИЕНТ, градиента, муж. (от лат. gradiens восходящий) (научн.). Изменение какой нибудь величины на какую нибудь единицу длины. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
Градиент и его свойства
Градиентом функции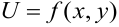 
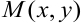
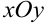
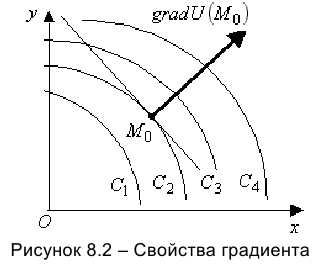
в данной точке 
называется вектор, расположенный в плоскости 
с началом в точке
Основное свойство градиента: направление градиента функции в точке является направлением быстрейшего возрастания функции, его модуль равен наибольшей скорости возрастания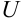 
в заданной точке.
Другое свойство градиента: он перпендикулярен касательной линии уровня, проходящей через точку начала градиента.
Иллюстрация свойств градиента — на рисунке 8.2. Показаны линии уровня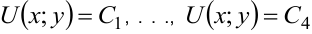 
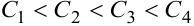
, причем 
.
Через точку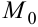 
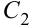
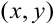
, лежащую на линии с уровнем 
проведены касательная и градиент, которые перпендикулярны друг другу. Градиент направлен в сторону возрастания функции 
.
8.6 Экстремум функции двух переменных. Необходимые и достаточные условия экстремума
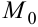
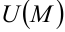
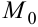
Точка называется точкой максимума функции 
, если значение функции в этой точке больше, чем её значение в любой другой точке некоторой (хотя бы малой) окрестности точки . Аналогично (с заменой «больше» на «меньше») определяется точка минимума функции.
Точки минимума и максимума объединяются под общим названием точки экстремума.
Для функции двух переменных точка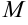 
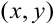
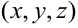
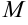
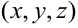
имеет две координаты для функции трёх переменных — три координаты 
. При этом окрестностью точки является открытый шар с центром в этой точке.
Поиск критических точек, т.е. точек в которых может быть экстремум функции 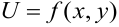, производится при помощи необходимого условия экстремума:
Решение системы (8.12) определяет координаты критических точек 
Однако необходимого условия мало для существования точек экстремума.
Нужно провести исследование критических точек с использованием достаточных условий экстремума.
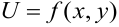
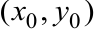
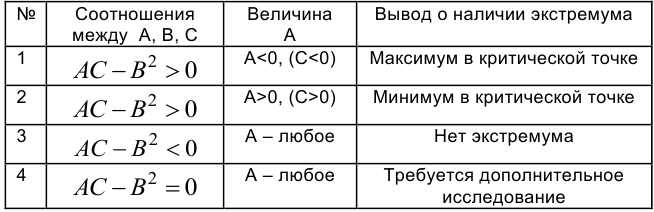
Для функции двух переменных введём обозначения для вторых частных производных в критической точке 
:
Достаточные условия приводим в таблице 4.
Таблица 4 — Достаточные условия экстремума функции двух переменных
Пример:
Дана функция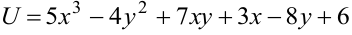 
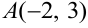
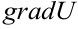
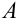
и точка 
. Найти градиент функции 
в заданной точке 
.
Решение:
Используем формулу градиента
Определяем частные производные и вычисляем их при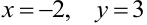 
.
При вычислении частной производной по одной из переменных вторая переменная считается постоянной величиной.
Значения частных производных подставляем в формулу градиента:
Ответ: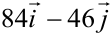 
.
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
СОДЕРЖАНИЕ
Мотивация
Обозначение
Определение
Когда функция также зависит от параметра, такого как время, градиент часто относится просто к вектору только его пространственных производных (см. Пространственный градиент ).
Декартовы координаты
В трехмерной декартовой системе координат с евклидовой метрикой градиент, если он существует, задается следующим образом:
Цилиндрические и сферические координаты
В цилиндрических координатах с евклидовой метрикой градиент задается следующим образом:
В сферических координатах градиент определяется как:
Общие координаты
Последнее выражение соответствует приведенным выше выражениям для цилиндрических и сферических координат.
Связь с производной
Связь с полной производной
С вычислительной точки зрения, учитывая касательный вектор, вектор можно умножить на производную (в виде матриц), что равносильно взятию скалярного произведения с градиентом:
( d ж п ) ( v ) знак равно [ ∂ ж ∂ Икс 1 ( п ) ⋯ ∂ ж ∂ Икс п ( п ) ] [ v 1 ⋮ v п ] знак равно ∑ я знак равно 1 п ∂ ж ∂ Икс я ( п ) v я знак равно [ ∂ ж ∂ Икс 1 ( п ) ⋮ ∂ ж ∂ Икс п ( п ) ] ⋅ [ v 1 ⋮ v п ] знак равно ∇ ж ( п ) ⋅ v <\ Displaystyle (df_
) (v) = <\ begin 
Дифференциальная или (внешняя) производная
Наилучшее линейное приближение дифференцируемой функции
Градиент связан с дифференциалом формулой
Если R n рассматривается как пространство векторов-столбцов (размерности n ) (действительных чисел), то можно рассматривать df как вектор-строку с компонентами
Линейное приближение к функции
Связь с производной Фреше
Как следствие, обычные свойства производной сохраняются для градиента, хотя градиент сам по себе не является производной, а скорее двойственен производной:
Другие свойства и применения
Наборы уровней
В более общем смысле, любая вложенная гиперповерхность в римановом многообразии может быть вырезана уравнением вида F ( P ) = 0 таким, что dF нигде не равно нулю. Тогда градиент F нормален к гиперповерхности.
Консервативные векторные поля и градиентная теорема
Градиент функции называется градиентным полем. (Непрерывное) поле градиента всегда является консервативным векторным полем : его линейный интеграл вдоль любого пути зависит только от конечных точек пути и может быть вычислен с помощью градиентной теоремы (основная теорема исчисления для линейных интегралов). И наоборот, (непрерывное) консервативное векторное поле всегда является градиентом функции.
Обобщения
Якобиан
Градиент векторного поля
Поскольку полная производная векторного поля является линейным отображением векторов в векторы, это тензорная величина.
(где используется обозначение суммирования Эйнштейна, а тензорное произведение векторов e i и e k является диадическим тензором типа (2,0)). В целом это выражение равно транспонированной матрице Якоби:
В криволинейных координатах или, в более общем смысле, на изогнутом многообразии градиент включает символы Кристоффеля :
Выражаясь более инвариантно, градиент векторного поля f может быть определен связностью Леви-Чивиты и метрическим тензором:
Римановы многообразия
где X j обозначает j- й компонент X в этой координатной карте.
Итак, локальная форма градиента принимает вид:
ГРАДИЕНТ ФУНКЦИИ
Смотреть что такое «ГРАДИЕНТ ФУНКЦИИ» в других словарях:
Градиент — Эта статья о математической характеристике; о способе заливки см.: Градиент (компьютерная графика) … Википедия
ГРАДИЕНТ — (лат.). Разность в барометрических и термометрических показаниях в разных местностях. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ГРАДИЕНТ разность в показаниях барометра и термометра в один и тот же момент… … Словарь иностранных слов русского языка
градиент — Изменение значения некоторой величины на единицу расстояния в заданном направлении. Топографический градиент — это изменение высоты местности на измеренном по горизонтали расстоянии. [http://www.oceanographers.ru/index.php?option=com… … Справочник технического переводчика
Градиент (в биологии) — Градиент в биологии, закономерное количественное изменение морфологических или функциональных, в том числе и биохимических, свойств вдоль одной из осей тела организма (или органа) на любой стадии его развития. Примеры Г.: убывание содержания… … Большая советская энциклопедия
градиент характеристики срабатывания функции дифференциальной защиты — [Интент] Тематики релейная защита EN gradient of the differential protection tripping characteristic … Справочник технического переводчика
Градиент — [gradient] вектор, направленный в сторону наискорейшего возрастания функции и равный по величине ее производной в этом направлении: где символами ei обозначены единичные векторы осей координат (орты) … Экономико-математический словарь
ГРАДИЕНТ — одно из основных понятий векторного анализа и теории нелинейных отображений. Градиентом скалярной функции векторного аргумента из евклидова пространства Е n наз. производная функции f(t).по векторному аргументу t, то есть n мерный вектор с… … Математическая энциклопедия
Градиент физиологический — – величина, отражающая изменение к либо показателя функции в зависимости от другой величины; напр., градиент парциального давления разность парциальных дав лений, определяющая диффузию газов из альвеол (акцинусов) в кровь и из крови в… … Словарь терминов по физиологии сельскохозяйственных животных
Градиент — I Градиент (от лат. gradiens, род. падеж gradientis шагающий) Вектор, показывающий направление наискорейшего изменения некоторой величины, значение которой меняется от одной точки пространства к другой (см. Поля теория). Если величина… … Большая советская энциклопедия
Градиент — (от лат. gradiens шагающий, идущий) (в математике) вектор, показывающий направление наискорейшего возрастания некоторой функции; (в физике) мера возрастания или убывания в пространстве или на плоскости какой либо физической величины на единицу… … Начала современного естествознания