что такое голономные системы
ГОЛОНОМНЫЕ СИСТЕМЫ
Полезное
Смотреть что такое «ГОЛОНОМНЫЕ СИСТЕМЫ» в других словарях:
Голономные системы — механические системы, в которых все связи (см. Связи механические) являются геометрическими (голономными), то есть налагающими ограничения только на положения (или перемещения за время движения) точек и тел системы, но не на величины их… … Большая советская энциклопедия
Неголономные системы — механические системы, на которые, кроме геометрических, налагаются ещё кинематические связи, не сводящиеся к геометрическим и называемые неголономными (см. Голономные системы). Примером Н. с. является шар, катящийся без проскальзывания по … Большая советская энциклопедия
НЕГОЛОНОМНЫЕ СИСТЕМЫ — механич. системы, на к рые, кроме геометрических, налагаются ещё кинематич. связи, не сводящиеся к геометрическим и наз. неголономными (см. ГОЛОНОМНЫЕ СИСТЕМЫ). Пример Н. с. шар, катящийся без проскальзывания по шероховатой плоскости. При этом… … Физическая энциклопедия
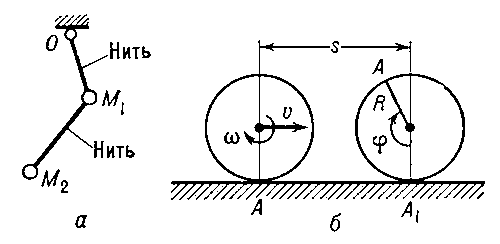
СВЯЗИ МЕХАНИЧЕСКИЕ — ограничения, налагаемые на положение или движения механич. системы. Обычно С. м. осуществляются с помощью к. н. тел. Примеры таких С. м. поверхность, по к рой скользит или катится тело; нить, на к рой подвешен груз; шарниры, соединяющие звенья… … Физическая энциклопедия
Лагранжа уравнения — 1) в гидромеханике уравнения движения жид кой среды, записанные в переменных Лагранжа, которыми являются координаты частиц среды. Из Л. у. определяется закон движения частиц среды в виде зависимостей координат от времени, а по ним… … Большая советская энциклопедия
Связи механические — ограничения, налагаемые на положение или движение механической системы. Обычно С. м. осуществляются с помощью каких нибудь тел. Примеры таких С. м.: поверхность, по которой скользит или катится тело; нить, на которой подвешен груз;… … Большая советская энциклопедия
Степеней свободы число — в механике, число независимых между собой возможных перемещений (См. Возможные перемещения) механической системы. С. с. ч. зависит от числа материальных частиц, образующих систему, и числа и характера наложенных на систему связей… … Большая советская энциклопедия
Голономная связь — Голономная связь механическая связь, налагающая ограничения только на положения (или перемещения) точек и тел системы. Математически выражается в виде равенства[1]: где qj обобщённые координаты, описывающие механическую систему, i=1…k … Википедия
Голономные системы
Полезное
Смотреть что такое «Голономные системы» в других словарях:
ГОЛОНОМНЫЕ СИСТЕМЫ — механич. системы, в к рых все связи (см. СВЯЗИ МЕХАНИЧЕСКИЕ) явл. геометрическими (голономными), т. е. налагающими ограничения только на положения (или на перемещения за время движения) точек и тел системы, но не на величины их скоростей. Напр.,… … Физическая энциклопедия
Неголономные системы — механические системы, на которые, кроме геометрических, налагаются ещё кинематические связи, не сводящиеся к геометрическим и называемые неголономными (см. Голономные системы). Примером Н. с. является шар, катящийся без проскальзывания по … Большая советская энциклопедия
НЕГОЛОНОМНЫЕ СИСТЕМЫ — механич. системы, на к рые, кроме геометрических, налагаются ещё кинематич. связи, не сводящиеся к геометрическим и наз. неголономными (см. ГОЛОНОМНЫЕ СИСТЕМЫ). Пример Н. с. шар, катящийся без проскальзывания по шероховатой плоскости. При этом… … Физическая энциклопедия
СВЯЗИ МЕХАНИЧЕСКИЕ — ограничения, налагаемые на положение или движения механич. системы. Обычно С. м. осуществляются с помощью к. н. тел. Примеры таких С. м. поверхность, по к рой скользит или катится тело; нить, на к рой подвешен груз; шарниры, соединяющие звенья… … Физическая энциклопедия
Лагранжа уравнения — 1) в гидромеханике уравнения движения жид кой среды, записанные в переменных Лагранжа, которыми являются координаты частиц среды. Из Л. у. определяется закон движения частиц среды в виде зависимостей координат от времени, а по ним… … Большая советская энциклопедия
Связи механические — ограничения, налагаемые на положение или движение механической системы. Обычно С. м. осуществляются с помощью каких нибудь тел. Примеры таких С. м.: поверхность, по которой скользит или катится тело; нить, на которой подвешен груз;… … Большая советская энциклопедия
Степеней свободы число — в механике, число независимых между собой возможных перемещений (См. Возможные перемещения) механической системы. С. с. ч. зависит от числа материальных частиц, образующих систему, и числа и характера наложенных на систему связей… … Большая советская энциклопедия
Голономная связь — Голономная связь механическая связь, налагающая ограничения только на положения (или перемещения) точек и тел системы. Математически выражается в виде равенства[1]: где qj обобщённые координаты, описывающие механическую систему, i=1…k … Википедия
Голономная система
Голономная система — механическая система, все механические связи которой можно свести к геометрическим (то есть, к голономным). Такие связи сводятся к ограничениям только на положения тел системы. Уравнения связи 
где 


Если все кинематические связи системы невозможно свести к геометрическим связям или их уравнения связи не могут быть проинтегрированы, то данная система будет неголономной.
Решение задач механики для голономных систем как правило проще, поскольку при этом можно воспользоваться многими разработанными методами и теоремами, например, уравнением Лагранжа, уравнением Гамильтона, уравнением Гамильтона-Якоби и др.
Пример
Рассмотрим математический маятник, состоящий из точечной массы, подвешенной на нити в поле сил тяжести. Если считать, что длина нити не изменяется, то уравнение связи можно записать в виде:
где 

Уравнение связи можно проинтегрировать, и как видно, оно не зависит от производных 

См. также
Ссылки
Полезное
Смотреть что такое «Голономная система» в других словарях:
ГОЛОНОМНАЯ СИСТЕМА — механическая система, в которой все Связи (см. Связи механические) являются голономными, т. е. геометрическими или сводящимися к геометрическим и налагающими ограничения только на положения (перемещения) точек и тел системы, но не на их скорости … Большой Энциклопедический словарь
голономная система — Механическая система, на которую наложены только голономные связи. [Сборник рекомендуемых терминов. Выпуск 102. Теоретическая механика. Академия наук СССР. Комитет научно технической терминологии. 1984 г.] Тематики теоретическая механика… … Справочник технического переводчика
голономная система — механическая система, в которой все связи (см Связи механические) являются геометрическими, т. е. налагают ограничения только на положения (или перемещения) точек и тел системы, но не на величины их скоростей, как это имеет место в неголономных… … Энциклопедический словарь
голономная система — holonominė sistema statusas T sritis chemija apibrėžtis Mechaninė sistema, kurios laisvės laipsnių skaičius lygus nepriklausomų koordinačių skaičiui. atitikmenys: angl. holonomic system rus. голономная система … Chemijos terminų aiškinamasis žodynas
голономная система — holonominė sistema statusas T sritis fizika atitikmenys: angl. holonomic system vok. holonomes System, n rus. голономная система, f pranc. système holonome, m … Fizikos terminų žodynas
ГОЛОНОМНАЯ СИСТЕМА — система материальных точек, либо не стесненная никакими связями, либо стесненная только геометрнч. связями, накладывающими ограничения на положения точек системы и могущими быть представленными в форме конечных соотношений вида Здесь t обозначает … Математическая энциклопедия
ГОЛОНОМНАЯ СИСТЕМА — механич. система, в к рой все связи (см. Связи механические) являются геометрическими, т. е. налагают ограничения только на положения (или перемещения) точек и тел системы, но не на величины их скоростей, как это имеет место в неголономных… … Естествознание. Энциклопедический словарь
голономная система — Механическая система, на которую наложены только голономные связи … Политехнический терминологический толковый словарь
Голономная связь — Голономная связь механическая связь, налагающая ограничения только на положения (или перемещения) точек и тел системы. Математически выражается в виде равенства[1]: где qj обобщённые координаты, описывающие механическую систему, i=1…k … Википедия
неголономная система — см. Голономная система. * * * НЕГОЛОНОМНАЯ СИСТЕМА НЕГОЛОНОМНАЯ СИСТЕМА, см. Голономная система (см. ГОЛОНОМНАЯ СИСТЕМА) … Энциклопедический словарь
ГОЛОНОМНАЯ СИСТЕМА
Смотреть что такое «ГОЛОНОМНАЯ СИСТЕМА» в других словарях:
Голономная система — Голономная система механическая система, все механические связи которой можно свести к геометрическим (то есть, к голономным). Такие связи сводятся к ограничениям только на положения тел системы. Уравнения связи записывают в виде: где… … Википедия
голономная система — Механическая система, на которую наложены только голономные связи. [Сборник рекомендуемых терминов. Выпуск 102. Теоретическая механика. Академия наук СССР. Комитет научно технической терминологии. 1984 г.] Тематики теоретическая механика… … Справочник технического переводчика
голономная система — механическая система, в которой все связи (см Связи механические) являются геометрическими, т. е. налагают ограничения только на положения (или перемещения) точек и тел системы, но не на величины их скоростей, как это имеет место в неголономных… … Энциклопедический словарь
голономная система — holonominė sistema statusas T sritis chemija apibrėžtis Mechaninė sistema, kurios laisvės laipsnių skaičius lygus nepriklausomų koordinačių skaičiui. atitikmenys: angl. holonomic system rus. голономная система … Chemijos terminų aiškinamasis žodynas
голономная система — holonominė sistema statusas T sritis fizika atitikmenys: angl. holonomic system vok. holonomes System, n rus. голономная система, f pranc. système holonome, m … Fizikos terminų žodynas
ГОЛОНОМНАЯ СИСТЕМА — система материальных точек, либо не стесненная никакими связями, либо стесненная только геометрнч. связями, накладывающими ограничения на положения точек системы и могущими быть представленными в форме конечных соотношений вида Здесь t обозначает … Математическая энциклопедия
ГОЛОНОМНАЯ СИСТЕМА — механич. система, в к рой все связи (см. Связи механические) являются геометрическими, т. е. налагают ограничения только на положения (или перемещения) точек и тел системы, но не на величины их скоростей, как это имеет место в неголономных… … Естествознание. Энциклопедический словарь
голономная система — Механическая система, на которую наложены только голономные связи … Политехнический терминологический толковый словарь
Голономная связь — Голономная связь механическая связь, налагающая ограничения только на положения (или перемещения) точек и тел системы. Математически выражается в виде равенства[1]: где qj обобщённые координаты, описывающие механическую систему, i=1…k … Википедия
неголономная система — см. Голономная система. * * * НЕГОЛОНОМНАЯ СИСТЕМА НЕГОЛОНОМНАЯ СИСТЕМА, см. Голономная система (см. ГОЛОНОМНАЯ СИСТЕМА) … Энциклопедический словарь
Ограничения, зависящие от скорости (также называемые полуголономными ограничениями), такие как:
обычно не являются голономными.
СОДЕРЖАНИЕ
Голономная система (физика)
В классической механике систему можно определить как голономную, если все связи системы голономны. Чтобы ограничение было голономным, оно должно быть выражено как функция :
Вступление
Терминология
ты → знак равно [ ты 1 ты 2 … ты п ] Т <\ displaystyle <\ overrightarrow > = <\ begin
ты → знак равно [ ты 1 ты 2 … ты п т ] Т <\ displaystyle <\ overrightarrow > = <\ begin
q → знак равно [ ты → ты ˙ → ] знак равно [ ты 1 … ты п ты ˙ 1 … ты ˙ п ] Т <\ displaystyle <\ overrightarrow > = <\ begin
q → знак равно [ ты → ты ˙ → ] знак равно [ ты 1 … ты п т ты ˙ 1 … ты ˙ п ] Т <\ displaystyle <\ overrightarrow > = <\ begin
Примеры
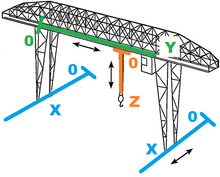
Козловой кран
Мы можем определить конфигурационное пространство системы как:
ты → знак равно [ Икс у z ] <\ displaystyle <\ overrightarrow > = <\ begin
Маятник
Жесткое тело
Частицы твердого тела подчиняются голономной связи
Пфаффова форма
Рассмотрим следующую дифференциальную форму ограничения:
Универсальный тест на голономные ограничения
мы можем использовать тестовое уравнение:
Если каждое тестовое уравнение верно для всего набора комбинаций для всех уравнений связи, система является голономной. Если это неверно хотя бы для одной тестовой комбинации, система неголономна.
Пример
Рассмотрим эту динамическую систему, описываемую уравнением связи в форме Пфаффа.
Подставляя термины, наше тестовое уравнение становится:
После вычисления всех частных производных получаем:
Упрощая, находим, что:
Мы видим, что наше тестовое уравнение верно, а значит, система должна быть голономной.
Мы закончили наш тест, но теперь, зная, что система голономная, мы можем захотеть найти уравнение голономной связи. Мы можем попытаться найти его, интегрировав каждый член формы Пфаффа и попытавшись объединить их в одно уравнение как таковое:
Легко видеть, что мы можем объединить результаты наших интеграций, чтобы найти уравнение голономной связи:
Ограничения постоянных коэффициентов
Для данного ограничения Пфаффа, где каждый коэффициент каждого дифференциала является константой, другими словами, ограничение в форме:
ограничение должно быть голономным.
и, следовательно, каждый член равен нулю, левая часть каждого тестового уравнения равна нулю, каждое тестовое уравнение истинно, и система является голономной.
Конфигурационные пространства двух или одной переменной
Любая система, которая может быть описана ограничением Пфаффа и имеет конфигурационное пространство или пространство состояний только из двух переменных или одной переменной, является голономной.
Мы можем доказать это как таковое: рассмотрим динамическую систему с конфигурационным пространством или пространством состояний, описанным как:
ты → знак равно [ ты 1 ты 2 ] Т <\ displaystyle <\ overrightarrow > = <\ begin
ты → знак равно [ ты 1 ты 2 λ ] Т <\ displaystyle <\ overrightarrow > = <\ begin
В заключение мы понимаем, что, хотя неголономные системы можно моделировать в форме Пфаффа, любая система, моделируемая в форме Пфаффа, с двумя или меньшим количеством степеней свободы (количество степеней свободы равно количеству членов в конфигурационном пространстве ) должен быть голономным.
ты → знак равно [ ты 1 ты 2 ты 3 ] Т <\ displaystyle <\ overrightarrow > = <\ begin
и набор ограничений, в котором одно или несколько ограничений имеют форму Пфаффа: