что такое главный вектор и главный момент плоской системы сил

Тема 1.4. Система произвольно расположенных сил

§1. Приведение пространственной системы сил к данному центру

Произвольной плоской системой сил называется совокупность сил, линии действия которых находятся в одной плоскости.

Теорема о параллельном переносе силы. Для переноса действующей на абсолютно твердое тело силы

из точки А (рис. 1, а) в точку О прикладываем в точке О силы и

Рис.1. Произвольной плоской системой сил

Рассмотрим теперь твердое тело, на которое действует какая угодно система сил

Чтобы сложить все полученные пары, надо геометрически сло­жить векторы моментов этих пар. В результате система пар заме­нится одной парой, момент которой или

называется главным моментом системы отно­сительно этого центра.

Рис.2. Система сил

Таким образом мы доказали следующую теорему, любая система сил, действующих на абсолютно твердое тело, при приведении к произвольно взятому центру О заменяется одной силой

Векторы и обычно определяют аналитически, т.е. по их проекциям на оси координат.

Выражения для R_x, R_y, R_z нам известны. Проекции век­тора на оси координат будем обозначать M_x, M_y, M_z. По тео­реме о проекциях суммы векторов на ось будет

Окончательно для определения проекций главного вектора и главного момента получаем формулы:

При этом главный вектор пространственной системы сил: R₀ = ΣP_i отличается от главного вектора плоской системы сил только наличием третьей компоненты, поэтому его модуль будет равен:

В зависимости от значений главного вектора и главного момента, а также от их взаимного расположения возможны следующие варианты приведения пространственной системы сил:

5) R₀ ≠ 0, M₀ ≠0 и главный вектор R₀ неперпендикулярен главному моменту M₀ — система эквивалентна скрещивающимся силам или динаме.

При этом скрещивающимися называются силы, которые непараллельны и не лежат в одной плоскости, а динамой называется система, состоящая из силы и пары сил, плоскость которой перпендикулярна этой силе.

Динама, приложенная к твердому телу, стремится вызвать его винтовое движение, которое представляет совокупность вращательного и поступательного движений.

Примечание: Для пространственной системы сил, как и для плоской, справедлива следующая Теорема Вариньона: Момент равнодействующей пространственной системы сил относительно произвольного центра (оси) равен геометрической (алгебраической) сумме моментов всех сил этой системы относительно данного центра (оси).

§2.Условия равновесия произвольной пространственной системы сил

Источник

Главный вектор и главный момент плоской системы сил

Главным вектором системы сил называется вектор R, равный векторной сумме этих сил:

Для плоской системы сил ее главный вектор лежит в плоскости действия этих сил.

Главным моментом системы сил относительно центра O называется вектор L_O, равный сумме векторных моментов этих сил относительно точки О:

Вектор R не зависит от выбора центра О, а вектор L_O при изменении положения центра О может в общем случае изменяться.

Для плоской системы сил вместо векторного главного момента используют понятие алгебраического главного момента. Алгебраическим главным моментомL_O плоской системы сил относительно центра О, лежащего в плоскости действия сил, называют сумму алгебраических моментов этих сил относительно центра О.

Главный вектор и главный момент плоской системы сил обычно вычисляется аналитическими методами.

Главный вектор и главный момент плоской системы сил

В аналитическом методе для вычисления главного вектора и главного момента используются проекции сил F_ix, F_iy и координаты x_i, y_i точек их приложения.

Модуль R главного вектора плоской системы сил и его направляющие косинусы e_x, e_у вычисляются по следующим формулам:

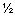
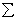
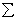
R = (R_х + R_y) ; e_x = R_x / R; e_y = R_у / R; R_x = F_ix; R_y = F_iy.

Алгебраический главный момент L_O плоской системы сил относительно центра O ( начала координатных осей ) вычисляется по формуле:

Здесь во вторую сумму выделены алгебраические моменты M_k пар сил (F_k, F‘_k).

В случаях, когда плечи h_i всех сил определяются достатосно просто ( например, если силы параллельны координатным осям Ox и Oy ), величина L_O может быть вычислена по формуле:

L_O = 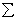± F_i h_i + M_k.

Лемма о параллельном переносе силы

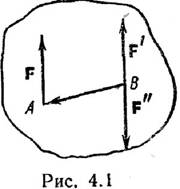
Докажем лемму: Сила, приложенная в какой-либо точке твердого тела, эквивалентна такой же силе, приложенной в любой другой точке этого тела, и паре сил, момент которой равен моменту данной силы относительно новой точки приложения. Пусть в точке А твердого тела приложена сила F (рис. 4.1). Приложим теперь в точке В тела систему двух сил F’ и F²-, эквивалентную нулю, причем выбираем F’=F (следовательно, F»=–F). Тогда сила F

0. Но, с другой стороны, система сил (F, F’, F») эквивалентна силе F’ и паре сил (F, F»); следовательно, сила F эквивалентна силе F’ и паре сил (F, F»). Момент пары (F, F») равен M=M(F,F»)=BAxF, т.е. равен моменту силы F относительно точки В M=M_B(F). Таким образом, лемма о параллельном переносе силы доказана.

Основная теорема статики

Пусть дана произвольная система сил (F₁, F₂. F_n). Сумму этих сил F=åF_k называют главным вектором системы сил. Сумму моментов сил относительно какого-либо полюса называют главным моментом рассматриваемой системы сил относительно этого полюса.

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Источник

Техническая механика

Плоская система произвольно расположенных сил

Лемма о параллельном переносе силы

Лемма: механическое состояние твердого тела не нарушится, если данную силу перенести параллельно первоначальному положению в произвольную точку тела, добавив при этом пару, момент которой равен моменту данной силы относительно новой точки приложения.

Описанный выше перенос силы можно показать на примере.

Приведение плоской системы произвольно расположенных сил к данному центру

Приведением системы сил называется замена ее другой системой, эквивалентной первой, но более простой.

Теорема: плоская система произвольно расположенных сил в общем случае эквивалентна одной силе, приложенной в центре приведения и одной паре сил.

Эта новая система эквивалентна данной.

Плоская система сил, приложенных в одной точке, эквивалентна одной силе, которая равна векторной сумме этих сил и приложена в той же точке, следовательно:

Эту силу назовем главным вектором данной системы.

Главный вектор плоской системы произвольно расположенных сил равен векторной сумме всех сил системы и приложен в центре приведения.

Графически главный вектор выражается замыкающей стороной силового многоугольника, построенного на данных силах.
Аналитически модуль главного вектора можно вычислить по формуле:

Плоская система пар эквивалентна одной паре, момент которой равен алгебраической сумме моментов данных пар, следовательно,

Эту пару с моментом М_гл назовем главным моментом заданной системы сил.

Главный момент плоской системы произвольно расположенных сил равен алгебраической сумме моментов всех сил системы относительно центра приведения.

Таким образом, всякая плоская система сил в общем случае эквивалентна системе, состоящей из силы и пары сил, следовательно, теорема доказана.

Не следует считать, что главный вектор и главный момент имеют чисто формальное значение, введенной для удобства доказательства, и что их можно найти только с помощью вычислений. Нередко отдельно действующие на тело силы определить трудно или даже невозможно, а главный вектор или главный момент этих сил найти сравнительно легко. Так, например, число точек контакта и модули сил трения между вращающимся валом и подшипником скольжения, как правило, неизвестны, но главный момент этих сил можно определить простым измерением.
Еще один пример: в характеристику электродвигателя входит не сила, с которой статор действует на ротор, а вращающий момент, являющийся, по сути, главным моментом этой силы.

Свойства главного вектора и главного момента

Свойства главного вектора и главного момента заключаются в следующем:

1. модуль и направление главного вектора данной системы не зависят от выбора центра приведения, так как при любом центре приведения силовой многоугольник, построенный на данных силах, будет один и тот же;

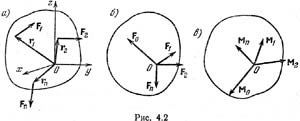
Пользуясь известным свойством пары сил, преобразуем главный момент М_гл так, чтобы силы пары F и F_Σ (рис. 4б) были равны по модулю и параллельны главному вектору F_гл :

Модуль равнодействующей можно определить по формуле:

а положение линии действия равнодействующей определяется плечом d по формуле:

В результате можно считать установленным, что главный вектор и равнодействующая векторно равны, но не эквивалентны.

Полученная формула является математическим выражением теоремы о моменте равнодействующей.

Теорема: момент равнодействующей силы относительно какой-либо точки, расположенной в плоскости действия сил, равен алгебраической сумме моментов составляющих сил относительно той же точки.

Применим доказанную теорему для определения положения линии действия равнодействующей F_Σ плоской системы n параллельных сил:

Выберем какую-либо точку О плоскости действия сил за центр моментов и согласно теореме Вариньона запишем:

Из последнего равенства определяем плечо d :

Различные случаи приведения плоской системы произвольно расположенных сил

На основании приведенных выше свойств главного вектора и главного момента можно выделить четыре возможных случая приведения плоской системы произвольно расположенных сил.

Аналитическое условие равновесия плоской системы произвольно расположенных сил

Как известно, плоская система произвольно расположенных сил находится в равновесии, когда главный вектор и главный момент равны нулю:

Но F_гл = F_Σ и равенство F_гл = 0 означает, что силовой многоугольник, построенный на силах данной системы, должен быть замкнут, следовательно, алгебраическая сумма проекций сил на каждую из двух осей координат x и y должна равняться нулю, т. е.:

Главный момент М_гл = ΣМ_О(F_i) и равенство М_гл = 0 означают, что алгебраическая сумма моментов сил данной системы относительно любого центра приведения равняется нулю, следовательно:

Итак, для равновесия плоской системы произвольно расположенных сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на оси координат x и y равнялись нулю, и чтобы алгебраическая сумма моментов этих сил относительно любой точки плоскости также равнялась нулю.

Условие равновесия упрощенно запишем в виде равенств:

Очевидно, что выведенные ранее условия равновесия системы сходящихся сил, системы непараллельных сил и системы пар являются частными случаями общего условия равновесия для плоской системы произвольно расположенных сил.

Следует отметить, что поскольку аналитические условия равновесия справедливы для любых прямоугольных осей координат, то в процессе решения задачи или при проверке правильности ее решения, оси координат можно изменять, т. е. одни уравнения проекций сил составлять для одной системы координат, а другие – для новой системы координат. Этот прием в некоторых случаях упрощает решение задачи или проверку правильности решения.

При решении задач статики аналитическим способом целесообразно составлять уравнения равновесия так, чтобы в каждом из них было как можно меньше неизвестных величин (в идеале – лишь одна неизвестная величина). Во многих случаях этого можно достигнуть рациональным выбором осей координат и центров моментов.

С примерами решения задач статики, основывающихся на условии равновесия плоской системы сил можно ознакомиться здесь.

Источник

Моментов бы Главный вектор и главный момент плоской системы сил

Главным вектором системы сил называется вектор R, равный векторной сумме этих сил:

Для плоской системы сил ее главный вектор лежит в плоскости действия этих сил.

Главным моментом системы сил относительно центра O называется вектор L_O, равный сумме векторных моментов этих сил относительно точки О:

Вектор R не зависит от выбора центра О, а вектор L_O при изменении положения центра О может в общем случае изменяться.

Для плоской системы сил вместо векторного главного момента используют понятие алгебраического главного момента. Алгебраическим главным моментом L_O плоской системы сил относительно центра О, лежащего в плоскости действия сил, называют сумму алгебраических моментов этих сил относительно центра О.

Главный вектор и главный момент плоской системы сил обычно вычисляется аналитическими методами.

геометрическая точка, неизменно связанная с твёрдым телом, через которую проходит равнодействующая всех сил тяжести, действующих на частицы этого тела при любом положении последнего в пространстве; она может не совпадать ни с одной из точек данного тела (например, у кольца). Если свободное тело подвешивать на нити, прикрепляемые последовательно к разным точкам тела, то направления этих нитей пересекутся в Ц. т. тела. Положение Ц. т. твёрдого тела в однородном поле тяжести совпадает с положением его центра масс (См. Центр масс). Разбивая тело на части с весами p_k, для которых координаты x_k, y_k, z_kих Ц. т. известны, можно найти координаты Ц. т. всего тела по формулам:

Ц. т. однородного тела, имеющего центр симметрии (прямоугольная или круглая пластины, шар, цилиндр и др.), находится в этом центре.ла равна нулю.Значит, систему пар или одну пар можно уравновесить только парой.

В расчетах конструкций на механическую надежность очень часто приходится оперировать такими характеристиками плоских фигур, как статический момент, осевой и полярный моменты инерции. Хотя вычисление вышеназванных геометрических характеристик относится к числу простейших задач интегрального исчисления, тем не менее, в силу их узкого прикладного значения они практически не рассматриваются во втузовском курсе высшей математики. По установившейся традиции геометрические характеристики плоских фигур изучаются в курсе сопротивления материалов.

Геометрические характеристики – числовые величины (параметры), определяющие размеры, форму, расположение поперечного сечения однородного по упругим свойствам деформируемого элемента конструкции (и, как следствие, характеризующие сопротивление элемента различным видам деформации).

Статический момент площади

Если на поверхности плоской геометрической фигуры площади А выделить элементарную площадкуdA (рисунок 1), то можно определить статические моменты и моменты инерции этой фигуры относительно осей х и у.

Под статическим моментом площади относительно некоторой оси понимается сумма произведений площадей элементарных площадок на расстояния от их центра тяжести до соответствующей оси:

статический момент площади относительно оси х

статический момент площади относительно оси у

Полученный результат позволяет сформулировать следующее определение: статический момент площади фигуры относительно оси, смещенной параллельно исходной, равен статическому моменту относительно исходной оси минус произведение площади этой фигуры на расстояние переноса.

Осевые и полярные моменты инерции всегда положительны и не равны нулю, а центробежный момент инерции может быть положительным, отрицательным и равным нулю в зависимости от положения сечения относительно осей. [1]Осевые и полярные моменты инерции всегда положительны; в то же время выражение ( А. [2]Осевые и полярные моменты инерции всегда положительны, так как в их выражения под знаки интегралов входят величины площадок dF ( всегда положительные) и квадраты расстояний этих площадок от данной оси или полюса. [3]Осевые и полярные моменты инерции всегда положительны, так как они представляют сумму положительных чисел. В нуль осевой момент инерции может обратиться только в одном частном случае, когда все материальные точки системы расположены на оси, относительно которой вычисляется момент инерции. [4]Осевые и полярные моменты инерции всегда положительны, так как в их выражения под зна си интегралов входят величины площадок dF ( всег ja положительные) и квадраты расстояний этих плока-док от данной оси или полюса. [5]Величины осевых и полярных моментов инерции всегда положительны и не могут быть равными нулю, поскольку в формулы ( 53), ( 54), ( 55) х, у и р входят в квадрате. [6]Отметим, что величины осевых и полярных моментов инерции всегда положительны. [7]Работа посвящена вопросам проектирования и исследования механизмов с фотоэлектронными устройствами, предназначенных для автоматических бесконтактных измерений и контроля линейных размеров деталей, определения различных геометрических параметров плоских фигур ( радиусов-векторов, площадей, положений центров тяжести, статистических моментов, осевых и полярных моментов инерции, моментов высших порядков), статистической обработки экспериментальных кривых и осуществления программированных перемещений. [8]

Воздействия, испытываемые стойкой от согнувшей ее руки (см. рис. 42), доской от груза (см. рис. 44), цилиндрическим стерж­нем болта при навинчивании гайки гаечным ключом (см. рис. 45) и т. д., представляют собой внешние силы илинагрузки. Силы, возникающие в местах закрепления стойки и опирания доски, называются реакциями.По способу приложения нагрузки делятся на сосредоточенные и распре­деленные).Виды и классификация нагрузок:Сосредоточенные нагрузки передают свое действие через,очень малые площади. Примерами таких нагрузок могут служить давление колес железнодорожного вагона на рельсы, давление тележки тали на монорельс и т. д.Распределенные нагрузки действуют на сравнительно большой площади. Например, вес станка передается через станину на всю площадь соприкосновения с фундаментом.По продолжительности действия принято различать постоянные и переменные нагрузки. Примером постоянной нагрузки может слу­жить давление подшипника скольжения — опоры валов и осей — и его соб­ственный вес на кронштейн.Переменной нагрузке подвержены в основном детали механизмов пери­одического действия. Одним из таких механизмов служит зубчатая переда­ча, у которой зубья в зоне контакта смежных пар зубчатых колес испыты­вают переменную нагрузку.По характеру действия нагрузки могут быть статическими и динамическими. Статические нагрузки почти не изменяются в тече­ние всего времени работы конструкции (например, давление ферм на опо­ры).Динамические нагрузки действуют непродолжительное время. Их воз­никновение связано в большинстве случаев с наличием значительных уско­рений и сил инерции.Динамические нагрузки испытывают детали машин ударного действия, таких, как прессы, молоты и т. д. Детали кривошипно-шатунных механиз­мов также испытывают во время работы значительные динамические на­грузки от изменения величины и направления скоростей, то есть наличия ускорений.

Деформа́ция (от лат. deformatio — «искажение») — изменение взаимного положения частиц тела, связанное с их перемещениемотносительно друг друга. Деформация представляет собой результат изменения межатомных расстояний и перегруппировки блоковатомов. Обычно деформация сопровождается изменением величин межатомных сил, мерой которого является упругое механическое напряжение.Деформации разделяют на обратимые (упругие) и необратимые (пластические, ползучести).Упругие деформации исчезают после окончания действия приложенных сил, а необратимые — остаются. В основе упругих деформаций лежат обратимые смещения атомов металлов от положения равновесия(другими словами, атомы не выходят за пределы межатомных связей); в основе необратимых — необратимые перемещения атомов на значительные расстояния от исходных положений равновесия(т.е. выход за рамки межатомных связей, после снятия нагрузки переориентация в новое равновесное положение).Пластические деформации — это необратимые деформации, вызванные изменением напряжений. Деформации ползучести — это необратимые деформации, происходящие с течением времени. Способность веществ пластически деформироваться называется пластичностью. При пластической деформации металла одновременно с изменением формы меняется ряд свойств — в частности, при холодном деформировании повышается прочность.

Деформация растяжения возникает тогда, когда на стержень или трос действуют внешние силы, приложенные к их концам, направленные в разные стороны и совпадающие с продольной осью этих тел.При этом наблюдается не только удлинение тела, но и уменьшение площади его поперечного сечения. Это и показано на модели тела, изображенной в верхней части таблицы.Деформация сжатия наблюдается в стержнях отно­сительно коротких под действием внешних сил, направ­ленных навстречу друг другу. Этот вид деформации не­возможен в тросах и стержнях относительно длинных. В длинных стержнях может возникнуть явление про­дольного изгиба тела или иного вида в зависимости от способа крепления стержня. При продольном изгибе возможно и частичное сжатие.Сжатие или любой другой вид деформации может иметь место под действием как статической, так и дина­мической нагрузки. В левой части таблицы показано сжатие короткого стержня гвоздя под ударом молотка. Если же стержень гвоздя будет достаточно длинным, то под действием продольной силы со стороны молотка гвоздь может согнуться, т. е. произойдет продольный из­гиб гвоздя. Этот вид деформации в школьном курсе фи­зики не рассматривается.Деформация сдвига возникает тогда, когда на тело, например брусок, действует сила параллельно основа­нию. В этом случае происходит смещение горизонталь­ных слоев в теле относительно друг друга без изменения их размеров.Отрезок, на который сместился верхний слой тела толщиной х, называют абсолютным сдвигом ∆x, угол α — углом сдвига. При малом угле сдвига (если угол α выражен в радианах):поэтому угол α часто называют относительным сдвигом. Деформации сдвига подвержены болтовые, заклепоч­ные и шпоночные соединения деталей. Этот вид дефор­мации наблюдается также в местах крепления балок, в шлицевых соединениях и т. д.; в элементах бытовых конструкций: стульях, столах и прочей мебели. В ниж­ней части таблицы показана деформация сдвига на при­мере одной ступеньки деревянной лестницы и штыревое соединение двух деталей, которое применяется при креплении автомобильных и тракторных прицепов.Следует иметь в виду, что в конструкциях этого вида деформации не бывает в чистом виде. Например, в за­клепочном соединении пренебрегают изгибом и растя­жением стержня заклепки.Деформации, представленные на второй таблице, не являются самостоятельным видом деформаций, так как они сводятся к двум наиболее простым — растяжению (сжатию) и сдвигу.Деформация изгиба возникает тогда, когда на балку, установленную на опорах, действуют поперечные силы (направлены перпендикулярно детали) и вызывают из­гиб, получивший название поперечного. Поперечному изгибу подвергаются фермы мостов, балки перекрытий в зданиях, а также доски пешеходных мостиков и т. д.Рассмотрим поперечный изгиб на модели, изображен­ной в верхней части таблицы. Представим себе балку, со­стоящую из продольных горизонтальных слоев. При из­гибе балки ее слои с выпуклой стороны растягиваются, а с вогнутой — сжимаются. Средний слой деформации не подвергается, его называют нейтральным. Наибольшему растяжению и сжатию подвергаются крайние слои. По­этому для уменьшения изгиба балки следует металл рас­пределять на верхней и нижней границах балки. В плос­кости нейтрального слоя толщина металла может быть небольшой. Этим объясняется создание двутавровых ба­лок. Если балка должна оказывать по всем направлени­ям одинаковое сопротивление изгибу, то наиболее выгод­ной будет трубчатая форма балки.Рамы велосипедов и мотоциклов, фабричные трубы, стебли многих растений и кости животных имеют труб­чатую форму.Деформация кручения сопровождается поворотом поперечных сечений стержня вокруг его оси. Такая де­формация имеет место в том случае, когда к концам стержня приложены пары сил, действующих в плоскос­тях концевых поперечных сечений и имеющих равные моменты. Моменты этих пар называют крутящими мо­ментами.Деформацию скрученного стержня можно предста­вить как результат поворота сечений. Угол поворота ф одного сечения относительно другого, находящегося от него на расстоянии l₀, называется углом закручивания стержня длиной l₀. Угол закручивания, отнесенный к единице длины стержня, называется относительным уг­лом закручивания:В средней части таблицы на модели показаны дейст­вующие силы и относительный поворот сечений (слоев) стержня при его закручивании. Деформация кручения в быту показана на примере работы стержня отвертки, а в технике — на примере работы сверла и шпинделя ручной дрели.Срез — предельный случай сдвига, когда силы упру­гости не могут уравновесить внешних сил. Примером сре­за в технике может служить разрушение заклепочных и болтовых соединений, в которых внешние силы действу­ют перпендикулярно оси болтов и заклепок, а также на примере штамповки деталей. На явлении среза основана работа режущего инструмента, в частности ножн

метод сечения Для определения любого внутреннего усилия используется метод сечений, который включает в себя 4 действия.

1) Режим стержень сечением MN на 2 части.

2) Отбрасываем одну из частей.

3) т.к. элемент находится в равновесии, то заменим действие отброшенной части внутренним силовым фактором.

4) Уравновешиваем оставшуюся часть уравнениями статики

При растяжении стержня его первоначальная длина L увеличивается до L₁. Разность между этими значениями называется абсолютным удлинением:∆l = L₁ — L.Отношение абсолютного удлинения к первоначальной длине называется относительным удлинением и обозначается ε:ε = ∆l / L.На основании закона Гука для упругих деформаций существует пропорциональная зависимость между нормальным напряжением и относительным удлинением:σ = Еε,где Е — коэффициент пропорциональности, называемый модулем упругости при растяжении, кгс/см 2 (Па).Для различных материалов, модуль упругости колеблется в широких пределах.Если представить деформацию сжатия, обратную растяжению, в процессе которой тело под действием внешних сил сжимается, то для обеих деформаций можно вывести общее условие прочности детали: действительное напряжение в детали не должно превышать допустимого при растяжении [σ]_р или при сжатии [σ]_сж.В тех случаях, когда из условия прочности надо определить площадь поперечного сечения детали, пользуются формулойF = P / [σ]_р(сж).

Источник